基于压缩感知DOA估计的稀疏阵列设计*
刘朋露,杨 洁
(西安邮电大学 通信与信息工程学院,西安 710121)
基于压缩感知DOA估计的稀疏阵列设计*
刘朋露*,杨 洁
(西安邮电大学 通信与信息工程学院,西安 710121)
根据格拉姆(Gram)矩阵优化测量矩阵的方法,给出了一种基于压缩感知波达方向(DOA)估计的均匀线阵的稀疏阵列设计方法。该方法不需要对阵列的输出数据进行压缩采样,直接利用稀疏阵列的输出数据,然后利用稀疏恢复算法求解DOA估计信息。实验仿真证明,相比于原均匀线阵,所提方法在阵元数目较少且信噪比较低的情况下具有更好的DOA估计性能。
压缩感知;测量矩阵;格拉姆矩阵;稀疏布阵;波达方向估计
1 引 言
基于压缩感知理论[1-2]的波达方向(Direction of Arrival,DOA)估计算法,通过测量矩阵对阵列的输出数据进行压缩采样,然后利用稀疏恢复算法求得DOA估计[3-5];当阵元数目较少时,以进行空域稀疏划分得到的阵列流型作为感知矩阵,根据阵列的输出信号,利用稀疏恢复算法求得DOA估计。两者的主要区别在于,前者对阵列的输出信号进行了压缩采样,而后者是直接利用阵列的输出数据进行DOA估计。相比基于信号子空间理论的DOA估计算法,基于压缩感知理论的DOA估计算法具有天然解相干能力,且在较少的采样快拍条件下仍具有较好的DOA估计性能。
基于阵列压缩采样的压缩感知DOA估计算法要求测量矩阵在满足一定正交性的前提下,其与稀疏字典应尽可能地不相关[6]。在稀疏恢复算法确定的前提下,测量矩阵的优化设计关系到稀疏恢复结果的精确度,即较好的测量矩阵能够在减少压缩采样数据的同时,保证稀疏恢复结果仍具有较高的精确度。
常用的测量矩阵有随机测量矩阵[7]和确定性测量矩阵。随机测量矩阵包括高斯随机测量矩阵、随机伯努利测量矩阵以及稀疏随机测量矩阵等。随机测量矩阵能够在很大程度上保证感知矩阵满足稀疏恢复的有限等距约束条件(Restricted Isometry Property,RIP),但具有不确定性、计算量大以及浪费存储资源的缺点。针对随机测量矩阵的上述缺点,已经提出了许多优化测量矩阵的方法[8-10]。关于确定性观测矩阵,文献[10-11]提出了一种基于格拉姆矩阵(Gram matrix)的测量矩阵设计方法,在保证感知矩阵满足稀疏重构条件的同时,使测量矩阵对阵元进行较少且不重复的采样。
根据压缩感知DOA估计中测量矩阵的设计方法,本文提出利用格拉姆矩阵对均匀线阵进行稀疏布阵,然后以进行稀疏布阵后的阵列作为入射信号的接收阵列,使上述第二种压缩感知DOA估计解法(以进行空域稀疏划分后的阵列流型作为感知矩阵)具有更好的DOA估计性能,尤其是在阵元数目较少且信噪比较低的情况下。
2 压缩感知DOA估计的基本原理
假设一均匀线阵(Uniform Linear Array,ULA)中包含N个阵元,该阵列的阵元间距为d,其值为入射信号的半波长。阵列共接收K个窄带入射信号的T个快拍数据,其采样时间点分别为t=1,2,3,…,T。则T快拍条件下的阵列输出信号可以表示为
X=AS+W。
(1)
式中:X是N×T维的阵列输出信号;S为K×T维的窄带入射信号;W为N×T维的加性高斯白噪声矩阵;A是N×K维的阵列流型矩阵,A=[a(θ1) a(θ2) …a(θK)],其中a(θk)是N×1维的阵列导向矢量,
a(θk)=[1 e-jαk… e-jαk(N-1)]T,k=1,2,…,K。
(2)
式中:αk=2π(d/λ)sin(θk)代表同一入射信号到达不同阵元与所选参考阵元之间的波程差,λ是入射信号的波长。
2.1 阵列的压缩采样模型
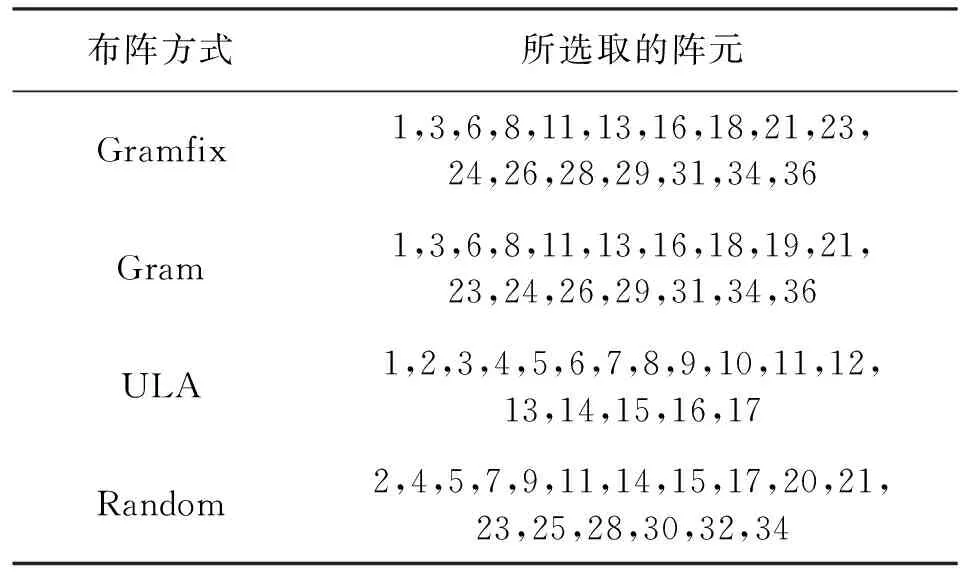
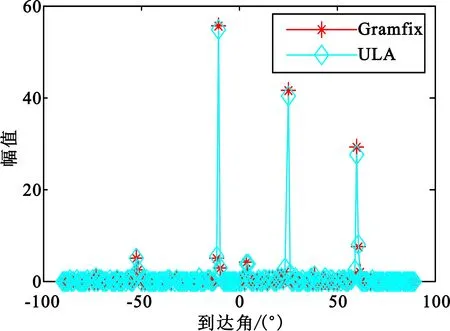
首先,介绍单快拍条件下的阵列压缩采样模型。假设x是一个N×1维的阵列输出信号矢量,且x=Ψz,其中Ψ是一个N×M维的稀疏字典,z是一个M×1维的系数矢量(即为x在稀疏字典Ψ下的投影系数),z中有K个非零元素(K代表来波个数),其包含着来波角度信息,即x是K稀疏的,且K< y=Φx=ΦΨz=ACSz。 (3) 式中:y是一个m×1维的测量矢量,m< 其次,介绍多快拍条件下的阵列压缩采样模型。假设一均匀线阵,其阵列模型如式(1)所示,则在压缩采样模型框架下的阵列输出信号可以表示为 X=ΨZ+W。 (4) 式中:Ψ是一个N×Ns维的稀疏矩阵,Ns代表空域划分网格数,Ψ中的每一列为式(2)中的a(θk),其中k=1,2,…,Ns;Z是一个Ns×T维的矩阵,Z中每一列都是K稀疏的,即每一列中有K个非零元素,其对应着来波角度信息;W是加性高斯白噪声矩阵。那么,在测量矩阵Φ已知的情况下,多快拍条件下的阵列压缩采样模型可以表示为 Y=ΦX=ΦΨZ+ΦW。 (5) 式中:Y为对阵列输出数据进行压缩采样后得到的数据。 式(5)中的Y是多个快拍条件下的压缩采样结果,对每个快拍下的阵列压缩采样数据,利用稀疏恢复算法求得DOA估计信息,然后按照式(6)综合每个快拍下的DOA估计信息[4]: (6) 2.2 以阵列流型作为感知矩阵的DOA估计模型 在以阵列流型作为感知矩阵的压缩感知DOA估计模型中,不需要对阵列的输出信号进行压缩采样,而是利用入射信号的天然稀疏特性,以进行空域稀疏划分后的阵列流型作为测量矩阵(即感知矩阵,因为信号具有天然稀特性,此时可以将稀疏字典理解成为一个单位阵),根据阵列的输出信号,然后利用稀疏恢复算法求解DOA估计信息。 根据式(1)中的阵列模型以及阵列输出信号X,则以阵列流型作为感知矩阵的DOA估计模型可以表示为 X=Φ′Ψ′Z=Φ′Z=A′CSZ。 (7) 由于式(7)中的Z具有天然稀疏特性,此时稀疏字典Ψ′是一个单位阵,则感知矩阵A′CS=Φ′Ψ′=Φ′。根据构建的阵列输出模型(1)可知,式(7)中的A′CS=Φ′=Ψ,Ψ的定义同式(3)中的Ψ,即稀疏字典。 综上所述,该算法以稀疏字典作为压缩感知DOA估计的感知矩阵,即感知矩阵A′CS=Φ′=ΦΨ。因此,可以结合格拉姆矩阵优化测量矩阵的方法,根据格拉姆矩阵优化测量矩阵所选取的采样阵元,优化式(5)中的测量矩阵Φ,根据Φ对原均匀线阵进行稀疏布阵,然后可以确定稀疏布阵后的阵列流型Φ′(该阵列流型为进行空域稀疏划分后,稀疏阵列所对应的阵列流型),最后利用该压缩感知DOA估计模型进行角度估计。 如前所述,该算法没有对阵列的输出信号进行压缩采样,而是直接利用阵列(稀疏布阵后的阵列)的输出信号,并且以进行空域稀疏划分后的稀疏阵列的阵列流型充当感知矩阵(即稀疏字典为单位阵),最后利用稀疏恢复算法求得DOA估计信息。 因此,构造如下的阵列优化模型[10-11]: (8) 当集合S较小时,可以采取遍历的方法,即遍历所有可能的采样阵元组合;当集合S较大时,可以采取遗传算法对测量矩阵进行优化。 综上所述,依据最优互相关系数C所对应的采样阵元,对原均匀线阵进行稀疏布阵,所得稀疏布阵方式,称为Gram;次最优互相关系数所对应的稀疏布阵方式,称为Gramfix,即修正的格拉姆矩阵。采用格拉姆矩阵优化测量矩阵时,其最优互相关系数所对应的采样阵元分布,与次最优互相关系数所对应的采样阵元分布情况相比,后者具有更好的非均匀特性。文献[14]证明,相比于均匀线阵,非均匀线阵下利用OMP算法进行稀疏恢复时,其具有更高的稀疏恢复精度,因此选取次最优互相关系数所对应的稀疏布阵(Gramfix)作为最佳稀疏布阵方式。然后,根据阵列的输出信号,利用以阵列流型作为感知矩阵的压缩感知DOA估计模型求得DOA信息。 4.1 仿真 假设原均匀线阵ULA(未进行阵列稀疏布阵)共有17个阵元,阵元间距为入射信号的半波长;有3个相干的远场窄带入射信号,来波角度分别为-10°、25°、60°;稀疏字典的空域稀疏划分个数为181,其按等角度进行划分;阵列的采样快拍数为60。假设当所估计的来波角度与实际信号的波达角度的误差绝对值小于1°时,则认为估计正确。在对信号进行稀疏布阵时,假设另一均匀线阵(用于抽取采样阵元的线阵)共有36个阵元,阵元间距为入射信号的半波长。根据优化模型(8),采取遍历或者遗传算法,分别选取最优(Gram)以及次最优(Gramfix)互相关系数C所对应的采样阵元构造测量矩阵,然后构造一随机测量矩阵(Random)(这里构造的随机测量矩阵为不重复地随机抽取36个阵元中的17个阵元)。根据以上3种测量矩阵,分别对原均匀线阵进行稀疏布阵。4种布阵方式所选取的阵元如表1所示。根据DOA估计模型(7),利用稀疏恢复算法求得波达方向。 表1 4种布阵方式所选取的阵元 在信噪比(Signal-to-Noise Ratio,SNR)为5 dB的情况下,原均匀线阵以及3种稀疏布阵阵列所对应的一次DOA估计结果如图1(a)所示;原均匀线阵以及次最优采样阵元所对应的稀疏阵列对应的一次DOA估计结果如图1(b)所示;在信噪比为5 dB的情况下,其所对应的30次独立重复试验的DOA估计结果如表2所示。 (a)4种阵列所对应的DOA估计结果 (b)原阵列以及次最优阵列对应的DOA估计结果 测量矩阵估计正确概率/%估计均方误差根Gramfix1000Gram1000ULA91.113.7832Random84.4411.5905 在信噪比为-5~21 dB的情况下,每个信噪比下进行30次独立重复试验。原均匀线阵以及3种稀疏布阵阵列所对应的DOA估计正确概率如图2(a)所示,所对应的DOA估计均方误差根如图2(b)所示。 (a)估计正确概率 (b)估计均方误差根 4.2 分析 由表1可知4种不同的阵列布阵方式所选取的阵元。其中,原均匀线阵为36个阵元(均匀分布阵列)中所抽取的前17个阵元;采用格拉姆矩阵对阵列进行优化布阵,对比其选取的最优(Gram)以及次最优(Gramfix)阵元,两者有略微的不同;随机布阵(Random)所选取的阵元为36个阵元中随机不重复抽取17个阵元。 在信噪比为5 dB时,利用稀疏恢复算法求解一次DOA估计,由图1(a)可以看出,4种阵列均能给出正确的DOA估计结果;图1(b)为次最佳采样阵元(Gram)构造的稀疏阵列与原均匀线阵的DOA估计结果的对比,两种阵列布阵方式都能给出正确的DOA估计结果,且两者估计结果在相同的估计角度处具有较小的幅值差。在相同信噪比下,进行30次独立重复试验,由表2可以看出,采用修正的格拉姆矩阵(Gramfix)对阵列进行稀疏布阵,其DOA估计正确概率最高、估计均方误差根最小。 在不同信噪比下,进行30次独立重复试验。由图2可知,当信噪比低于5 dB时,采用修正的格拉姆矩阵构造的稀疏阵列,与其他3种阵列相比,其具有相对较高的估计正确概率,且具有较低的估计均方误差根。 本文将利用格拉姆矩阵优化压缩感知DOA测量矩阵的方法应用于阵列的稀疏布阵中,通过不重复抽取均匀阵列中的若干阵元构造测量矩阵,以测量矩阵和稀疏字典的乘积作为感知矩阵,以感知矩阵为基础构造格拉姆矩阵,利用格拉姆矩阵构造优化模型,根据优化模型选取最佳采样阵元,以所选取的最佳采样阵元为依据对原均匀线阵进行稀疏布阵。 根据入射信号的天然稀疏性,以进行空域稀疏划分后的稀疏阵列的阵列流型作为感知矩阵,结合稀疏阵列的阵列输出,利用稀疏恢复算法求得波达方向。实验仿真证明,该稀疏布阵模型相比于原均匀线阵以及其他稀疏阵列,在信噪比较低时具有更好的DOA估计性能。 该方法是基于均匀线阵进行优化布阵,即所选取阵元的间距都是均匀线阵阵元间距的整数倍,则研究基于非均线阵以及其他阵型的优化布阵具有一定的意义。由于解稀疏前未对阵列输出信号进行压缩采样,因此,在阵元数目相同且数目较大的情况下,相比于阵列的压缩采样模型,以阵列流型作为感知矩阵的DOA估计算法具有相对较高的运算量。 [1] QAISAR S,BILAL R M,IQBAL W,et al.Compressive sensing:from theory to applications,a survey[J].Journal of Communications & Networks,2013,15(5):443-456. [2] 吴凌华,张小川. 压缩感知的发展与应用[J].电讯技术,2011,51(1):120-124. WU Linghua,ZHANG Xiaochuan. Development and application of compressed sensing[J].Telecommunication Engineering,2011,51(1):120-124.(in Chinese) [3] ANILA S B,DEEPA B,BHAI S,et al. Compressive sensing for array signal processing[C]//Proceedings of 2012 Annual IEEE/India Conference(INDICON).Kochi,India:IEEE,2012:555-560. [4] GUO X,SUN H.Compressive sensing for target DOA estimation in radar[C]//Proceedings of 2014 International Radar Conference.Lille,France:IEEE,2014:1-5. [5] 赵宏伟,刘波,谢广钱,等. 基于压缩感知的卫星干扰源定位[J].电讯技术,2015,55(5):467-471. ZHAO Hongwei,LIU Bo,XIE Guangqian,et al.Satellite interference location based on compressive sensing theory[J].Telecommunication Engineering,2015,55(5):467-471.(in Chinese) [6] WANG C Y,JING X U.Improved optimization algorithm for measurement matrix in compressed sensing[J].Systems Engineering & Electronics,2015,37(4):752-756. [7] PAZOS S,HURTADO M,MURAVCHIK C.DOA estimation using random linear arrays via compressive sensing[J].IEEE Latin America Transactions,2014,12(5):859-863. [8] LI G,ZHU Z,YANG D,et al.On projection matrix optimization for compressive sensing systems[J].IEEE Transactions on Signal Processing,2013,61(11):2887-2898. [9] JIANG Q R,BAI H,LI D,et al.Alternative optimization of sensing matrix and sparsifying dictionary for compressed sensing systems[C]//Poceedings of 2014 IEEE Industrial Electronics and Applications.Hangzhou:IEEE,2014:510-515. [10] ENDRA. Joint optimization of measurement matrix and sparse dictionary in compressive sensing[C]//Proceedings of 2012 International Conference on Compute and Communication Engineering(ICCCE).New York:IEEE,2012:420-425. [11] 张波,刘郁林,王开,等.基于概率稀疏随机矩阵的压缩数据收集方法[J].电子与信息学报,2014,36(4):834-839. ZHANG Bo,LIU Yulin,WANG Kai,et al.Compressive data gathering method basedon probabilistic sparse random matrices[J].Journal of Electronics and Information Technology,2014,36(4):834-839.(in Chinese) [12] WANG W,WU R.High resolution direction of arrival(DOA) estimation based on improved orthogonal matching pursuit(OMP) algorithm by iterative local searching[J].Sensors,2013,13(9):11167-83. [13] TROPP J A,GILBERT A C. Signal recovery from random measurements via orthogonal matching pursuit[J].IEEE Transactions on Information Theory,2008,53(12):4655-4666. [14] 刁鸣,高璐,高洪元,等.基于非均匀线阵的压缩感知波达方向估计[J].计算机工程,2015,41(10):83-87. DIAO Ming,GAO Lu,GAO Hongyuan,et al.Direction of arrival estimation usingcompressed sensing based on non-uniform liner array[J].Computer Engineering,2015,41(10):83-87.(in Chinese) Design of Sparse Arrays Based on Compressive Sensing DOA Estimation LIU Penglu,YANG Jie (School of Communication and Information Engineering,Xi′an University of Posts and Telecommunications,Xi′an 710121,China) According to the method of optimizing measurement matrix through Gram matrix,a sparse array design method for uniform linear array(ULA) based on compressive sensing direction of arrival(DOA) estimation is proposed. Without compressive sampling,this method can draw the DOA estimation results through the sparse recovery algorithm by using the output data of sparse array directly. The experimental simulation results show that,especially under the condition of less array elements and lower signal-to-noise ratio(SNR),this method has a better performance of DOA estimation compared with the original ULA. compressive sensing;measurement matric;Gram matrix;sparse array;DOA estimation 10.3969/j.issn.1001-893x.2017.04.002 刘朋露,杨洁.基于压缩感知DOA估计的稀疏阵列设计[J].电讯技术,2017,57(4):382-386.[LIU Penglu,YANG Jie.Design of sparse arrays based on compressive sensing DOA estimation[J].Telecommunication Engineering,2017,57(4):382-386.] 2016-09-02; 2016-12-14 Received date:2016-09-02;Revised date:2016-12-14 国家自然科学基金青年科学基金资助项目(61402365);陕西省科技攻关计划(2013K06-33) TN911.7 A 1001-893X(2017)04-0382-05 刘朋露(1990—),男,河南新乡人,2014年获学士学位,现为硕士研究生,主要研究方向为通信信号处理及应用; Email:emailoflpl@163.com 杨 洁(1976—),女,陕西西安人,2006年获硕士学位,现为副教授,主要从事阵列信号处理、自适应信号处理及其在通信与雷达中的应用研究。 *通信作者:emailoflpl@163.com Corresponding author:emailoflpl@163.com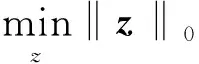
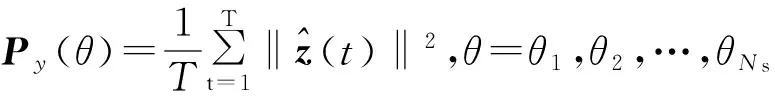

3 格拉姆矩阵优化测量矩阵的方法

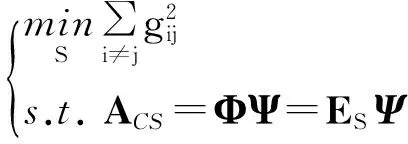

4 仿真与分析




5 结 论


