一种提高轨道预测精度的递推估值算法
张 冰,乔建江
(中国电子科技集团公司第五十四研究所,河北 石家庄 050081)
一种提高轨道预测精度的递推估值算法
张 冰,乔建江
(中国电子科技集团公司第五十四研究所,河北 石家庄 050081)
测控雷达系统必须具有跟踪目标速度快、精度要求高等特点,并且当目标信号受到障碍物遮挡目标丢失后,要求测控系统能够对目标运行轨迹进行精确预测,提高目标重新出现后的重捕概率。为了提高轨道预测精度,在轨道跟踪算法基础上引入了最小二乘法数据外推理论,使用最小二乘法对丢失后的目标轨道数据进行了预估值外推分析,并针对最小二乘法数据外推随着时间增长精度快速变差的缺点,引入了递推的最小二乘法。通过实验和数据分析表明,使用递推最小二乘法能够大幅度提高目标丢失5 s内的轨道预测精度,满足雷达测控系统记忆跟踪和目标重捕的要求。
轨道预测;递推估值;最小二乘法;记忆跟踪
0 引言
为了完成航空或航天飞行器再入飞行境内段航区和着落段航区的遥控、遥测、跟踪定位和图像传输等任务要求,测控系统需要对目标进行快速地捕获跟踪,为了能使跟踪系统正常工作,当目标信号受到障碍物遮挡丢失时,要求对跟踪目标轨道进行预测,一旦目标重新进入视场,能够快速准确地对目标实施重捕[1-2]。跟踪目标轨迹预测实质是利用目标进入盲区前飞行测量数据,估出各阶导数推出目标飞行轨迹进行跟踪,从而使目标出盲区时不丢失[3]。目前使用较普遍的方法是拉格朗日插值算法和牛顿插值算法,拉格朗日插值算法在差值区间中部插值精度较高,但在靠近插值区间两端则会出现龙格现象,影响整个插值的精度,从而限制了其在数据处理和拟合中的应用[4]。而牛顿插值算法插值数据较多时,需要大量的计算时间,从而影响系统实时性[5]。此外,目标发生机动时,由于运动的速度和方向发生改变,也会造成实时跟踪的困难,为了补偿跟踪误差,达到实时、稳定跟踪目标的目的,本文在分析了传统最小二乘法轨道预测精度的基础上,提出了一种实时递推的最小二乘预测跟踪算法,能够满足大多数雷达测控系统中对目标丢失后重捕的需要[6]。
1 最小二乘法
最小二乘法是一种数学优化技术,它通过最小化误差的平方和找到一组数据的最佳函数匹配,它用最简单的方法求得一些绝对不可知的真值,而令误差平方之和为最小[7]。为了确定n个不可直接测量的未知量X1,X2,…,Xn的估计量x1,x2,…,xn,可对该n个未知量Yn进行直接测量,测得数据为l1,l2,…,ln。设未知量Y1,Y2,…,Yn的估计值用y1,y2,…,yn表示,则线性参数的测量方程为:
(1)
相应的估计量为:

(2)
由于测量误差的存在,估计值与实测值不完全相等,其误差方程为:

(3)
由最小二乘法可知,参数的最佳值应该在残余误差平方和为最小的条件下给出,即应满足

(4)
利用极值的偏导数为零的性质,现用残余误差平方和对t个未知量求偏导,并令其为零,可得到t个方程,整理后得:
(5)
此方程即为线性参数最小二乘法的正规方程,方程的个数等于未知量的个数,有唯一确定的解,将其表示为矩阵形式:
(6)
令

则式(6)可表示为:
ATV=0。
(7)
式(3)可表示为:

(8)
把式(7)代入式(8),得

(9)
由此可得未知量最佳估计值的矩阵解为:

(10)
本系统中选用的二次抛物线拟合函数为:
y=b0+b1x+b2x2。
(11)
待定系数有3个,即b0,b1和b2。设定输入值x即为采样时刻,做变量变换,
α0=1,α1=x,α2=x2。
(12)
则原函数变为:
y=b0α0+b1α1+b2α2。
(13)
设选定观测次数为n,则

(14)
在确定了观测次数n后,矩阵A可完全确定,那么在计算式(1)中,[ATA]-1AT可视为已知,可预先计算其结果并作为数据表存于程序中,从而大大减少了程序执行过程中的运算量,节省程序的处理时间。
若令
T=[ATA]-1AT,
(15)
则计算式(10)变为:
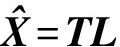
(16)
这样,将矩阵T作为数据表放在程序末端,实际上求拟合曲线的参数只需要进行一次矩阵与列向量之间的乘法运算就可以了。
2 数据预测与结果分析
预测精度是反映预测效果好坏的重要指标[8],本文中采用系统随机误差来度量预测效果的好坏,目标角度预测值的系统随机误差表示如下:


采用某雷达天线实际测角定位数据作为试验数据,首先分析了通过使用不同观测点,预测不同时刻产生的系统随机误差,如图1所示。

图1 观测值数据个数对预测值误差影响
从图1中可以看出,对于系统模型数据,当观测点为5个时,通过最小二乘法预测的轨道数据与实际数据产生了很大的偏差,并且随着预测点数的增加,误差急剧增大,最终导致了数据的发散。随着观测点数逐渐增加,预测数据与理论数据的偏差逐渐减小,但是当观测点个数超过某个程度时,预测数据的随机误差再次增大,因此对于观测个数n的确定,需要根据系统的状态特征等多种因素综合考虑,如果n取值太小,容易造成较大的变化幅度,导致预测数据误差较大;当n取值太大的时候,预测公式对于系统的变化反应速度较慢,预测值不能及时反映出系统的真实变化规律,同样造成较大的误差[10]。
通过上面的试验数据可知,当观测次数为50时得到了较好的预测估值效果,基本上可以满足一般系统的需求,采用50次观测数据进行外推估值结果与实际测量数据结果对比如图2所示。从结果中可以看出,随着估值量的增加,误差仍然在不断增大,当估值量达到一定程度后,系统仍然有发散的趋势。为了解决以上问题,可以引入递推最小二乘法。
递推最小二乘法就是当被辨识系统在运行时,每取得一次新的观测数据后,就在前一次估计结果的基础上,利用新引入的观测数据对前次估计的结果根据递推算法进行修正,从而递推地得出新的参数估计值,这样随着新的观测数据的逐次引入,一次接一次地进行参数估计,直到参数估计值达到满意的精确度为止。采用递推最小二乘法进行数据外推结果如图3所示。从分析数据中可以看出,递推最小二乘法估值数据能够真实有效地反映实际数据的变化趋势,估值数据总体精度得到了很大的提升。

图2 目标观测值与预测值比较

图3 采用递推算法观测值与预测值比较
当目标进入盲区导致信号丢失后,测控系统自动转入记忆跟踪工作方式,并且通常要求在5 s内能够准确预报目标运动轨迹,完成重新发现目标后的自动重捕[11]。从上述的分析中可以看出,使用传统的最小二乘法预测目标轨迹误差随着时间的推移急剧增大,无法满足记忆跟踪对目标重捕的要求。而使用递推最小二乘法,通过将系统测量数据对前次的估值结果进行不断地修正,可以大幅度提高估值精度,减小估值误差,在5 s内的估值结果完全能够满足对目标重捕的需要,提高了目标捕获概率。
3 结束语
递推最小二乘法在轨道预测方面具有计算简单、实时性强和预测精度高等优点,但其预测精度受到观测数据的选取和外推数据长度等因素的影响,只有通过合理选取观测数据,才能获得一定时间内的高精度预测数据。
由上述分析可以看出,该算法解决了以往算法预测精度低、计算复杂等缺点,在雷达测控领域的应用完全能够满足系统轨道预测和记忆跟踪的需求,配合跟踪方式的适当调整,可以达到目标丢失后的快速重捕和稳定跟踪的目的,相比于常规的轨道数据预测算法具有一定的优势。
[1] 黄玉学.智能天线技术[J].无线电通信技术,2006,32(4):27-29.
[2] 张 晓,薛锋章.智能天线内置一体化合路校准网络[J].移动通信,2014,38(2):76-79.
[3] 高京龙.单脉冲单通道跟踪体制精度分析方法[J].无线电工程,2007,37(7):32-34.
[4] 李 强,崔 岩.切比雪夫多项式在单台经纬仪记忆跟踪中的应用[J].激光与光电子学进展,2013(4):172-176.
[5] 戴聚岭.多项式插值法在工程计算中应用[J].福建电脑,2006(4):178-179.
[6] 米芳彬,徐小刚,梁 健.基于有限记忆最小二乘的雷达误差配准算法[J].无线电工程,2016,46(2):65-68.
[7] 孙明轩,黄宝健.迭代学习控制[M].北京:国防工业出版社,1999.
[8] 费业泰.误差理论与数据处理[M].北京:机械工业出版社,1994.
[9] 章劲松,林宇生,谭云华.GEO卫星多波束天线指向测量方法与误差分析[J].无线电通信技术,2015,41(6):58-60.
[10] 李连升,张志英,刘绍球.现代雷达伺服控制[M].北京:国防工业出版社,1987.
[11] 董旭锋,张志彪.天线伺服系统的冗余设计[J].无线电通信技术,2012,38(6):42-44.
张 冰 男,(1981—),硕士,工程师。主要研究方向:测控雷达伺服控制系统。
乔建江 男,(1974—),硕士,高级工程师。主要研究方向:测控雷达伺服控制系统。
Recursive Estimation Algorithm for Improving Orbit Prediction Precision
ZHANG Bing,QIAO Jian-jiang
(The54thResearchInstituteofCETC,ShijiazhuangHebei050081,China)
The antenna of TT&C system must have characteristics of high dynamic capability and high measurement precision.When the signal is shielded from the antenna and the target is lost,it is required to predict the orbit and re-capture the target quickly.The least square method is analyzed to improve the measurement precision.A recursive-estimation algorithm is used to solve the problem of the least square method in satellite orbit forecast.The test and data analysis indicate that the orbit prediction precision is improved greatly through the recursive-estimation algorithm,and it can meet the requirement of memory track and target re-capture.
satellite orbit forecast;recursive-estimation algorithm;least square method;memory track
10.3969/j.issn.1003-3106.2017.05.20
张 冰,乔建江.一种提高轨道预测精度的递推估值算法[J].无线电工程,2017,47(5):84-86,94.[ZHANG Bing,QIAO Jianjiang.Recursive Estimation Algorithm for Improving Orbit Prediction Precision[J].Radio Engineering,2017,47(5):84-86,94.]
2017-02-28基金项目:国家重点基础研究发展规划基金资助项目(2013CB37900)。
TN850
A
1003-3106(2017)05-0084-03

