设备跟踪质量综合评定方法应用

苟茹君,韩迎春，吕 辉

(1.宇航动力学国家重点实验室，陕西 西安 710043； 2.西安卫星测控中心，陕西 西安 710043)

设备跟踪质量综合评定方法应用

苟茹君1,2,韩迎春2，吕 辉2

(1.宇航动力学国家重点实验室，陕西 西安 710043； 2.西安卫星测控中心，陕西 西安 710043)

针对工程试验过程中需要对多套测量设备的跟踪质量进行评定，以便快速、准确地选择测量数据的实际需求，对层次分析法原理及应用步骤和对数最小二乘法原理进行了简要介绍，通过实际算例对方案层、准则层和目标层进行选取，建立了测站设备跟踪质量评定的层次分析模型；综合层次分析法、隶属度和对数最小二乘方法对设备跟踪质量进行综合评定，结果表明与专家评定的结论一致。该方法将定性分析与定量分析相结合，减少了单纯的人为定性评定的随机不确定性，为测量设备跟踪质量评定提供了一种选择。

测量设备；质量评价；层次分析法；隶属度；对数最小二乘法

0 引言

在航天发射试验过程中，测量设备的跟踪质量对工程试验的进展会产生很大的影响，特别是在发生关键事件时，为了选择有效数据，更需要对测量设备跟踪质量进行评定。一般情况下，由专家根据测量设备的特点，结合测量弧段以及关键事件，对测量设备的跟踪质量进行定性评定，但这样做，无形中增加了人为的不确定性。

在不能通过数学模型准确表达，或者由于系统复杂难于建立数学模型的情况下，层次分析法(Analytic Hierarchy Process，AHP)能够为多目标、多准则或无结构特性的复杂问题决策提供便捷思路[1]，将定性与定量相结合而被应用到相关领域中。文献[2]依照金融机构的特点，建立了数据质量评估的层次模型，应用模糊层次分析方法对征信系统的数据进行评估，获得了良好的效果。文献[3]通过对侦察方案的分析，通过选择相应的信息建立了层次结构模型，利用层次分析方法对侦察方案进行效能的评估。文献[4]提出了确定层次分析法权重的新方法，给出了传统层次分析法标度到模糊层次分析法标度的转换方法。文献[5-7]对模糊判断矩阵的一致性进行了研究，文献[6]中提出了一种同步一致性算法和基于矩阵一致性指标的多判断矩阵合成方法。

本文在对测量设备的跟踪状况进行深入分析的基础上，结合实际情况，选择测站设备跟踪的时间、跟踪数据的乱散与丢失和完成关键事件的情况等因素作为方案层，对评定结果敏感性强的因素作为准则层，测量设备跟踪质量评定作为目标层，建立了测站设备跟踪质量评定的层次分析模型，综合层次分析法、隶属度和对数最小二乘方法，对测站设备的跟踪质量进行了评定。

1 层次分析法原理及应用步骤

层次分析法是美国著名的运筹学家Saaty等人在20世纪70年代提出的一种定性与定量分析相结合的多准则决策方法[8-9]，广泛应用于决策、预测和评估等方面，是系统工程中常有的方法[10]，隶属度是模糊数学中的理论[11]，通过它能够将层次分析法与模糊数学相结合，将复杂的、难以用数学方法精确描述的问题，结合数学的逻辑性，实现对事物的定性与定量分析，从而达到了将复杂问题简单化、层次化的方法[12]。

层次分析法与隶属度结合进行评价的主要步骤如下[13]：

① 确定指标域和评价域。依照具体问题，确定被评价方案的指标域和评价域：

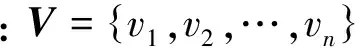
按照被评价方案的评价目的，指标域的确定应该以尽可能反应被评价方案的性能为目的。指标域可以一层也可以多层。评价域一般以人们的生活习惯或者行业准则为基础，划分为含义明显、能反应不同评价结果的元素集合。

② 构造评价目标的层次结构。按照上下层之间的联系与支配作用，综合考虑各层诸因素对评价结果的影响程度，将影响因素分组，按照目标层、准则层和方案层的形式排列起来，应用结构图表示其构成。

cij>1，

cii=1,i=1,2,…,n。

1～9标度法是构造判断矩阵常用的方法[14-15]，其含义如表1所示。

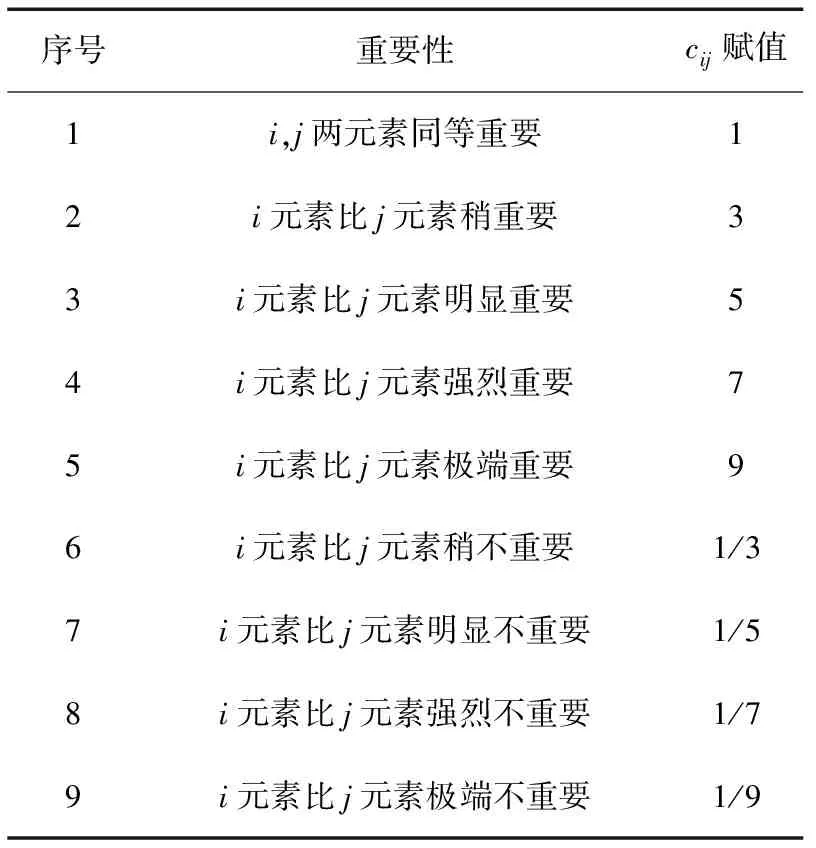
表1 1～9标度法的定义

注意：

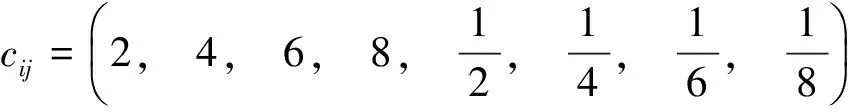
表示重要性等级介于：

之间。

④ 确定权重。在层次分析方法中，权重的确定通常需要检验判断矩阵的一致性，但是考虑到层次分析法本身是定性与定量相结合的方法，对权重的精确度要求不高。因此可以采用对数最小二乘法求判断矩阵的特征值的方法确定权重：

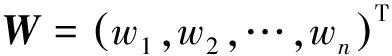
⑤ 建立评判矩阵。从单个的指标出发，依照每个指标对评价域的隶属度，通过多名专家打分的方法，对被评方案的方案层进行量化，从而确定出每个指标的隶属度，得到隶属度关系矩阵R：

式中，rij为某个被评方案从指标ui来看对vi等级的隶属度。

⑥ 计算评价向量及评价结果。计算评价向量，并依照最大隶属度原则得到评价结果：

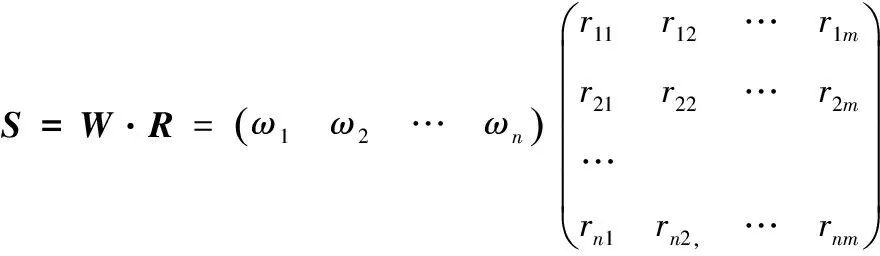
式中，S为评价结果向量，它反映了该方案总体上对评价域V中各模糊子集的隶属度，再应用最大隶属度原则即可以得到评价结果。

2 对数最小二乘法原理

在实际决策时，鉴于问题的复杂性及思维的局限性，决策者给出的判断矩阵一般不是一致的，为此要对判断矩阵进行调整，这个过程比较繁琐。为了避免这样的过程，针对层次分析方法本身具有的模糊性，考虑应用最优化方法来解决权值的确定问题。

对数最小二乘方法的求解过程如下：

① 构造偏差函数

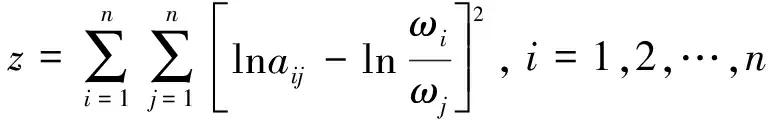
(1)

② 建立最优化模型。为了得到方案的解，基于式(1)，可以建立下列最优化模型：

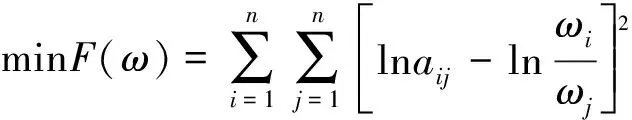
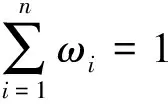
(2)

式中，ωi>1,i=1,2,…,n。

③ 方程求解。为了求解上述最小化问题，则令

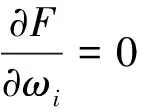
(3)

解此方程组，得到解为：

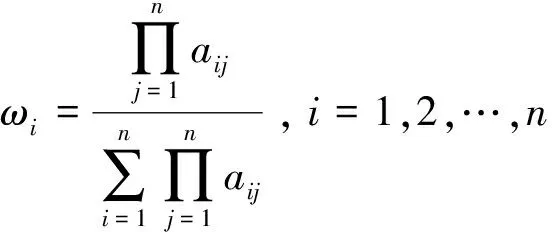
(4)

3 实际算例

在工程试验过程中，经常会对试验段落进行跟踪测量。在整个测量过程中，测量设备在给定的时间段中完成跟踪任务情况、对关键事件的处理是最重要的。在跟踪过程中数据不丢、不错、不乱是测量设备完成任务的重点。跟踪完成后，为了提高后续的工作效率，数据的及时传送便显得重要。基于上述原因，选择跟踪时间、数据统计特性、关键事件和数据传送时间作为方案层，同时选择数据测量段落的完整性、数据的有效性、关键事件完成情况和数据传输的及时性作为准则层，以设备跟踪质量评定作为目标层，建立如图1所示的层次分析模型，应用对数最小二乘法确定权系数，最大隶属度原则得到评定结果。

3.1 建立层次结构及评价域

依照设备的状况，选择对评价目标比较敏感的因素，并构造层次结构图如图1所示。

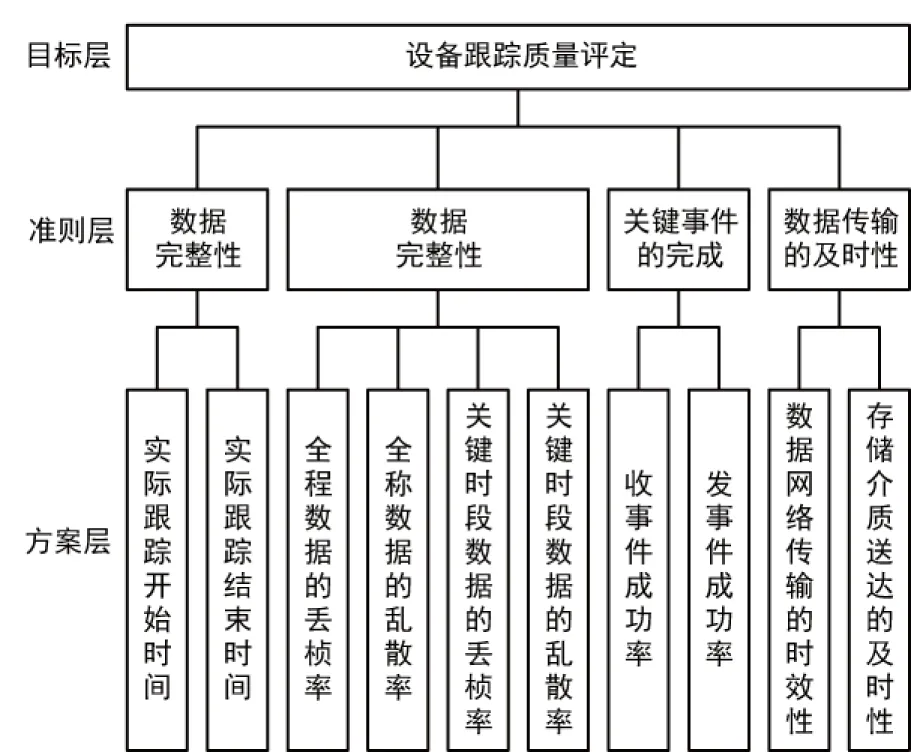
图1 设备跟踪质量评定层次结构模型

给定的评定域为：V= {优 良 中 差}；

给定的方案层的因素构成指标域。

3.2 构建判断矩阵

依照相对重要性，应用1～9标度法，对准则层建立判断矩阵A，针对准则层中的数据完整性、数据有效性、关键时间的完成情况和数据传输的即时性分别建立判断矩阵A1、A2、A3和A4。

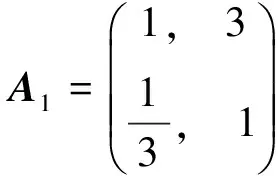
3.3 确定权重

为了确定各级权重，应用式(1)构造偏差函数，应用式(2)建立最优化模型，应用式(3)建立方程组，最后应用式(4)求得上述各级的权重为：

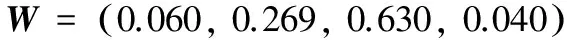
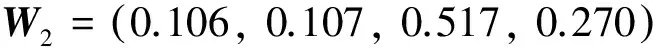
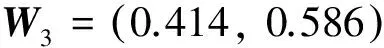
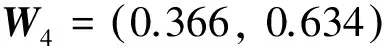
3.4 建立模糊评判矩阵

第1次选择评价为优秀的指标元素构成集合U1；第2次选择评价为良好的指标元素，与U1元素一起构成集合U2；第3次选择评价为中等的指标元素，与U2中的元素一起构成集合U3；第4次选择评价为差的指标元素，与U3中的元素一起构成集合U4。

设第i次选择的次数为ki，每次选择指标元素的个数构成公比为2的等比数列。最后剩余的元素不足2ki的时候，将所有的剩余元素作为最后一次的选择结果，选择终止。打分评价结果如表2所示。

表2 专家评价结果

由表2可以看出，在对关键事件U7和U8的评价上，专家意见存在分歧。综合表2结果，可以判断本次跟踪等级为：良。

在表2中，分别统计U1～U10中相同的判断结果，对统计结果进行归一化处理得到相应的模糊判断矩阵为：

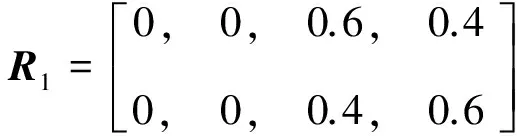
3.5 计算单因素评价结果

根据权重和模糊评判矩阵，计算单因素评判结果如下：

3.6 计算评价结果

进行二级评判计算并用最大隶属度原则计算得到最终的评判结果为：

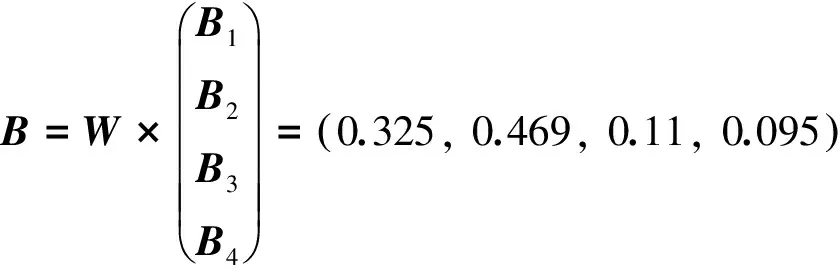
式中，最大数据为0.469，对应的跟踪质量评定结果为“良”。

4 结束语

本文应用层次分析法对测量设备的跟踪情况进行了评定，从计算结果可以看出，最终等级计算结果与专家的评定结果一致，文中的方法也可以推广应用到其他领域的质量评定。

在层次分析方法中，各层元素的选择没有特定的准则可以遵守，在实际的工程中，用户依据各自的特点进行确定，难免还有主观的因素。各层不同因素的选择对决策结果会产生不同的影响，下一步对层次中各元素的选择进行进一步研究，探寻对决策敏感度更高、影响更大的因素，提高决策结果的可靠性。

[1] 许树伯.实用决策方法—层次分析法原理[M].天津:天津大学出版社，1988：14-76.

[2] 徐 清.基于模糊层次分析方法的地方性金融机构企业征信系数据质量评估[J].征信，2014(3)：29-32.

[3] 程 浚，陈 岗，周继权.基于模糊层次分析方法的侦察方案效评估[J].指挥信息系统与技术，2013，4(4)：47-50.

[4] 兰继斌，徐 扬，霍良安，等.模糊层次分析法权重研究[J].系统工程理论与实践，2006(9)：107-112.

[5] 王艳梅，赵希男，郭 梅.一种调整模糊判断矩阵一致性的方法[J].模糊系统与数学，2006，20(3)：89-94.

[6] 徐 华，邱 彤，赵近松.模糊判断矩阵构造和矩阵一致性检验的同步方法[J].清华大学学报(自然科学版)，2010，50(6)：913-916.

[7] 舒 陵.基于模糊数学的液压挖掘机故障诊断[J].吉首大学学报(自然科学版)，2010，36(3)：52-55.

[8] 夏富洲，刘富奎，陈栋梁.不确定型层次分析法在渡槽结构状态评估中的应用[J].武汉大学学报(工学版)，2012，45(3)：277-281.

[9] 项 磊，杨 新，张 扬，等.基于层次分析法与模糊理论的卫星效能评估[J].计算机仿真，2013，30(2)：55-61.[10] 史睿冰，姚兴太，史圣兵，等.基于层次分析法的通信系统效能评估[J].计算机工程与设计，2013，34(12)：4 131-4 136.

[11] 韩立岩，汪培庄.应用模糊数学[M].北京：首都经济贸易大学出版社，1989：73-76.

[12] 周媛媛，周学军，田培根，等.模糊层次分析法在海缆安全评估中的应用[J].海军工程大学学报，2014，26(4)：59-62.

[13] 杜 栋，庞庆华，吴 炎.现代综合评价方法与案例精选[M].北京：清华大学出版社，2008：11-19.

[14] 段守福，杨 凯，汪 军，等．航空无线电通信系统作战效能评估[J].火力与指挥控制，2010，35(11)：117-119.[15] 轩永波，黄长强，王 勇，等.基于灰色层次分析法的空间武器作战效能评估[J].空军工程大学学报(自然科学版)，2011，12(2)：32-37.

[16] 李石良，王 瑛.对判断矩阵对数最小二乘法的新思考[J].统计与决策，2008(16)：164-165.

苟茹君 女，(1971—)，硕士，高级工程师。主要研究方向：数据分析与处理。

韩迎春 男，(1974—)，硕士，高级工程师。主要研究方向：数据分析与处理。

Application of Method for Evaluating the Tracking Quality of Measurement Equipment

GOU Ru-jun1,2,HAN Ying-chun2,LV Hui2

(1.StateKeyLaboratoryofAstronauticDynamics,Xi’anShaanxi710043,China; 2.Xi’anSatelliteControlCenter,Xi’anShaanxi710043,China)

In engineering test process,we need evaluate the tracking quality of multiple sets of measurement equipment,so as to perform fast and accurate selection of measurement data.Firstly,the principle of AHP and application steps and logarithmic least squares principle are introduced.Through a practical example,the case layer,criterion layer,and target layer are chosen respectively.And the analysis model of station equipment tracking quality assessment level is established.Next,such methods like AHP,membership,and least squares are integrated to evaluate the quality of tracking equipment.And the results are consistent with the conclusion of expert evaluation.The method combines qualitative analysis with quantitative analysis,reduces the uncertainty of the qualitative assessment of human,and provides a choice for the quality evaluation。

measurement equipment;quality evaluation;analytic hierarchy process;membership;logarithmic least square method

10.3969/j.issn.1003-3106.2017.05.19

苟茹君,韩迎春,吕 辉.设备跟踪质量综合评定方法应用[J].无线电工程,2017,47(5):79-83.[GOU Rujun,HAN Yingchun,LV Hui.Application of Method for Evaluating the Tracking Quality of Measurement Equipment[J].Radio Engineering,2017,47(5):79-83.]

2017-02-21

国家自然科学基金资助项目(11503096)。

TN99

A

1003-3106(2017)05-0079-05