跨大气层飞行器气动伺服弹性稳定性分析方法研究
惠俊鹏,杨 超
(1. 中国运载火箭技术研究院研究发展中心,北京,100076;2. 北京航空航天大学,北京,100191)
跨大气层飞行器气动伺服弹性稳定性分析方法研究
惠俊鹏1,2,杨 超2
(1. 中国运载火箭技术研究院研究发展中心,北京,100076;2. 北京航空航天大学,北京,100191)
跨大气层飞行器通常采用翼身组合体外形,机体结构柔性大,飞行控制系统通道之间交联耦合且通频带宽、再入扰动因素复杂、气动加热严重,上述因素可能导致气动伺服弹性或热气动伺服弹性问题。考虑外界干扰不确定性、飞行器模型摄动和控制通道耦合等因素,跨大气层飞行器需进行多通道交联耦合气动伺服弹性鲁棒稳定性分析。通过弹性飞行器动力学建模、非定常气动力拟合、伺服系统和飞行控制系统建模,建立了气动伺服弹性系统的闭环模型。在此基础上对 Nyquist方法、最小奇异值法以及结构奇异值µ方法等气动伺服弹性稳定性分析方法进行了分析与讨论,得出相关结论。
跨大气层飞行器;气动伺服弹性;稳定性;结构奇异值;µ方法
0 引 言
飞行器气动伺服弹性(Aeroservo-elasticity,ASE)问题是一门涉及弹性飞行器结构、非定常气动力以及飞行控制系统三者相互作用的多学科技术问题。该问题实质为:飞行器在飞行中受扰动而发生运动,这种运动包含了飞行器的刚体运动和机体结构的弹性振动。传感器同时接收刚体运动信号和结构弹性振动信号,如伺服控制系统通频带覆盖飞行器主要固有频率,则舵面的反馈偏转中将额外增加一部分频率较高的偏转运动(相应的会增加一部分舵面非定常气动力和惯性力)。这是由于控制系统的反馈而额外作用于飞行器的控制力,这部分控制力将影响飞行器的运动,由此形成飞行器气动伺服弹性系统,如图1所示[1,2]。

图1 气动伺服弹性系统
气动伺服弹性稳定性分析是指对于给定的飞行器,研究气动伺服弹性闭环系统的稳定性。
1 跨大气层飞行器ASE分析的特点
相比于其它飞行器,跨大气层飞行器具有以下特点[3,4]:
a)飞行器机体尺寸大,机体结构固有频率较低,容易发生气动弹性/气动伺服弹性问题;
b)再入飞行中气动加热效应显著,可能引起飞行器结构刚度发生变化,给飞行器气动弹性特性带来不利影响;
c)飞行器飞行速域、空域范围大,飞行过程中高度及动压变化范围大,要求飞行器具有一定的气动伺服弹性鲁棒稳定性;
d)飞行器通常采用翼身组合体或升力体气动布局,气动特性复杂,扰动因素复杂;
e)飞行器常采用多个气动操纵面进行三通道飞行控制,各通道之间存在相互影响作用,难以完全解耦,是典型的多通道交联耦合系统;
f)飞行过程中燃料的消耗易导致飞行器质量特性发生变化,给飞行器的动力学建模引入显著摄动。
由于上述因素,跨大气层飞行器气动伺服弹性分析面临如下问题:
a)飞行包线宽,飞行过程中外界扰动因素复杂;
b)受气动加热和燃料消耗影响,飞行器模型可能发生摄动;
c)飞行器控制通道之间存在交联耦合,这种交联耦合作用对系统稳定性的影响往往是不利的。
因此对于跨大气层飞行器而言,多通道交联耦合气动伺服弹性系统建模与分析技术是研制过程中需解决的重要问题。
2 跨大气层飞行器气动伺服弹性系统建模
跨大气层飞行器气动伺服弹性系统是由飞行器弹性机体子系统、伺服作动子系统、飞行控制子系统等组成的闭环系统,因此建立飞行器气动伺服系统模型需要建立各个子系统的数学模型。
2.1 弹性机体动力学模型
综合考虑飞行器的刚体和弹性自由度,建立弹性飞行器运动方程。为避免采用结构体轴系或风轴系而出现刚体运动与弹性运动之间的惯性耦合项,选用一个平均轴系,可以满足在任何时刻弹性变形引起的相对线动量和角动量均为0的条件,即[3,5,6]:

式中 d为弹性结构上某一质量块dm相对于平均轴系的位置向量;δ δt为相对于平均轴系的时间导数。
设ijk,, 为平均轴系的单位向量,考虑弹性模态之间的正交性,可得系统的动能表达式为
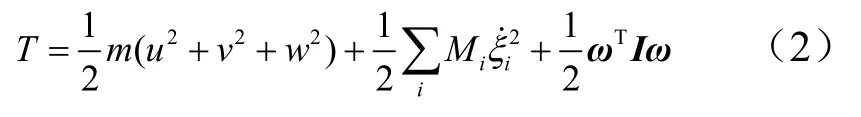
式中 m为飞行器总质量;Mi为第i阶弹性模态的广义质量; ξi为广义弹性模态坐标;u,v,w及 ωT分别为飞行器相对于惯性系的线速度和角速度用在平均轴上的分量,其中, ωT=[ p qr ];I为转动惯性张量。
考虑系统的弹性应变势能,利用结构的自由振动弹性模态,系统应变能为

式中 ωi为自由振动的第i阶弹性模态的固有频率。
设Fx,Fy,Fz和 Mx,My,Mz分别为外力、外力矩在平均轴上的分量,应用拉格朗日方程可得弹性飞行器的运动方程为

式中 Qξi为对应于第i阶弹性模态的广义力。
由于飞行器结构弹性模态与刚体模态正交,在小扰动假设下,飞行器的弹性运动方程为[3,6]

式中 K为广义刚度矩阵;V0为远前方来流速度;g为重力加速度;θ0为平衡状态处的俯仰角;M为广义质量矩阵,M=diag(M1,M2,…,Mn);A为广义非定常气动力影响系数矩阵;φ和θ为惯性系到平均轴系的转动欧拉角;ξ,η和δ分别为弹性模态、刚体运动模态和控制面偏转。
2.2 广义非定常气动力模型
广义非定常气动力建模是建立飞行器气动伺服弹性系统状态空间方程的重要步骤。目前工程上常采用有理函数拟合方法进行广义非定常气动力建模。主要有以下3种拟合方法[7,8]:
a)最小二乘法(Least Squares,LS);
b)最小状态法(Minimum State,MS);
c)修正的矩阵 Padé法(Modified Matrix Padé,MMP)。
LS法气动力拟合计算量小、精度最高,但气动增阶最大;MMP方法精度介于LS法与MS法之间,而气动增阶也较大;MS法计算精度略有降低,但仍适合工程应用,其所导致的状态空间气动弹性模型阶数最小。
采用LS法进行非定常气动力拟合,可以通过减少拟合模态数及滞后根个数降低被控对象阶数。气动系数矩阵Q的LS法有理函数近似式Qap为[6]
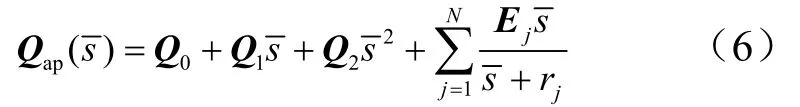
式中 rj为实常数,称作滞后根。
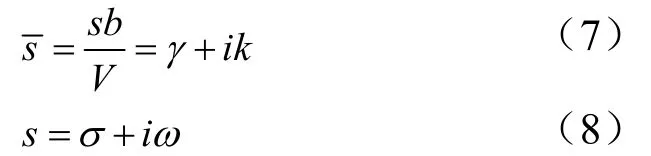
式中 b为参考长度;ω为振动圆频率;σ为运动衰减率;V为飞行速度。
于是可将弹性飞行器的线性小扰动方程转化为状态空间形式:

式中 AS为系统矩阵;xS为状态向量;BS为控制矩阵;uS为输入向量。
2.3 传感器模型
飞行器常采用加速度计和角速率陀螺来感受机体运动信息,这些传感器测得的信号是飞行器相对于惯性参考系的速度和角速度在仪器敏感轴上的分量[3],这些运动信号受仪器位置和弹性振动的影响。输出方程可以表示为

式中 CS为输出矩阵;DS为直接传递矩阵。
2.4 伺服作动器模型
飞行器采用舵机来驱动控制面偏转,常用的有液压舵机、电动舵机和气动舵机。考虑常用的电液舵机,其舵机传递函数一般可表示为[3,9]

式中ec为输入控制指令;δ为控制面偏转响应。
将此传递函数进行变换,可得到以 ec为控制向量的舵机状态空间方程。
2.5 气动伺服弹性闭环系统模型
将弹性机体环节、非定常气动力环节、传感器环节、舵机环节等联接起来,可得飞行器ASE广义受控对象模型:

式中AP为广义受控对象系统矩阵;BP为控制矩阵;CP为输出矩阵; xP为广义受控对象状态向量;u为作动器控制指令;y为传感器输出的运动信息。
这个模型可以用于气动伺服弹性系统的稳定性分析和主动控制律设计。
飞行器控制系统的 k阶控制律可用状态空间形式表达为

式中 AK为系统矩阵;BK为控制矩阵;CK为输出矩阵。
将广义受控对象与飞行控制系统进行联立,得到飞行器气动伺服弹性闭环系统方程:

式中r为参考输入。
至此,可采用该模型进行飞行器ASE系统稳定性分析。
3 跨大气层飞行器气动伺服弹性稳定性分析
3.1 气动伺服弹性鲁棒稳定性
对于完全不受摄动的线性系统,其动态特性由状态空间方程描述,稳定性由状态矩阵的特征值来判断。但在实际当中,不确定性是客观存在的。由于不确定性摄动的影响,真实系统工作时有可能偏离所预料的性能,甚至失去稳定性。鲁棒性(Robustness)即为动力学系统在一定的不确定性摄动影响下,仍能稳定且正常工作的能力。对于跨大气层飞行器,由于飞行过程中气动伺服弹性系统模型参数摄动和外界复杂扰动因素的影响,气动伺服弹性鲁棒稳定性比传统的稳定性更具有现实意义。
3.2 Nyquist方法
对于如图1所示ASE闭环系统,其开环传递函数可以由各个环节的传递函数得到:
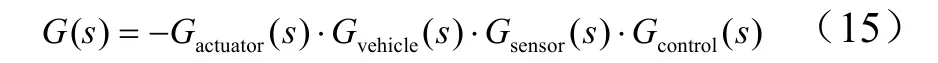
在关心的频率范围内计算系统开环传递函数,在复平面内作图,可得系统开环传递函数的乃氏图,如图 2所示。由此可以得到闭环系统的幅值裕度和相位裕度。相位裕度即开环乃氏曲线上模值等于1的矢量与负实轴的夹角,在伯德图上相当于处的相位与π-的角差;幅值裕度即开环乃氏曲线与负实轴相交点模值的倒数,在伯德图上,即相当于相位为 π-时,幅值的绝对值,即:

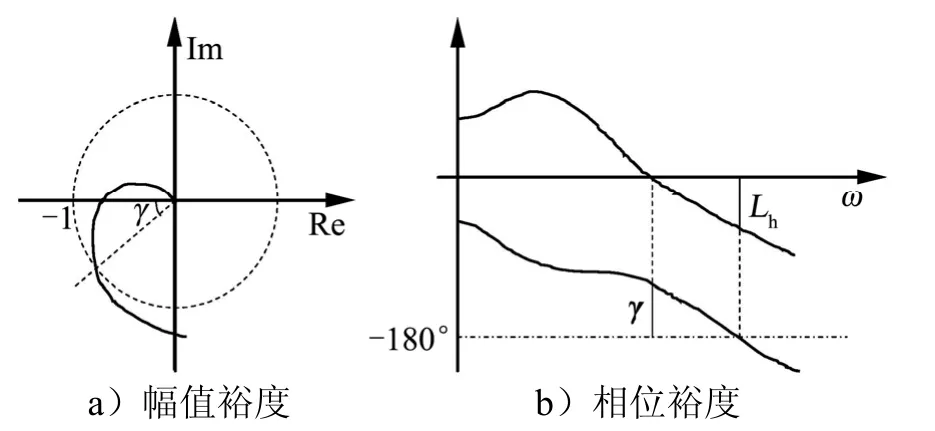
图2 传统的稳定裕度示意
上述稳定裕度概念仅在一定程度上反映系统的鲁棒稳定性,不能考虑系统是否能承受某类具体的参数摄动。例如,对于如图3所示的特定情况[10],传统的稳定裕度表征方法失去了其有效性。

图3 传统稳定裕度概念的失效
对于多输入、多输出(Multiple Input Multiple Output,MIMO)系统,相应的也有广义Nyquist稳定判据,但该方法可能给出过于乐观的结论。在线性系统范围内比较有效的分析工具是最小奇异值方法和结构奇异值µ方法,它们能较好地解决线性系统的鲁棒性问题。其中最小奇异值方法只能处理非结构化的鲁棒稳定性问题,对于参数不确定性的鲁棒稳定性分析的问题,比较有效的方法是结构奇异值µ方法。
3.3 最小奇异值方法
对于MIMO系统,以最小奇异值原理为基础的鲁棒稳定性分析方法为MIMO系统提供了一种可用的鲁棒稳定性分析工具。
典型的受乘法摄动的闭环控制系统如图4所示。
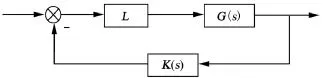
图4 反馈系统乘法摄动
摄动矩阵L可表示为

L为气动伺服弹性系统摄动项的增益kj和相位φj组成的对角矩阵,每一项表示对应输入分量的摄动量。对于标称系统,L为单位阵。
标称系统的回差矩阵为

基于奇异值理论的鲁棒稳定性判据为若标称系统稳定,则受扰系统稳定的充分条件是在全频域范围内,有以下不等式成立[11]:

实际计算中,为满足系统的裕度需要,一般要求闭环系统回差矩阵的最小奇异值不小于 0.6,即≥0.6。
3.4 结构奇异值µ方法
基于最小奇异值理论的鲁棒稳定性分析方法通常给出偏保守的结果,而结构奇异值µ方法考虑了不确定性摄动集合的块对角结构,克服了分析中的保守性,能更加精确地对具有结构和非结构不确定性摄动的系统进行鲁棒稳定性分析。
对于线性控制系统,分析其鲁棒稳定性时可按照在标称系统中加入摄动影响因子的方法来考虑,如图5所示。

图5 鲁棒稳定性分析
M(s)和Δ(s)均是稳定的。在某一频率处,广义系统算子M∈Cn×n,不确定性算子Δ是由重复标量块和满块矩阵组成的复数块对角的矩阵,其集合记为

复数矩阵M∈Cn×n关于不确定性Δ的结构奇异值µ(M)为[12]

结构奇异值µ与系统鲁棒稳定性关系为:设α>0,对于所有满足的Δ(s),如图5所示的闭环系统是鲁棒稳定的充分必要条件是[13]:

结构奇异值µ分析方法就是将分析的对象转化为图 5所示的标准模型,计算在不确定性摄动矩阵Δ作用下的广义系统M的结构奇异值 ()µM ,据此判断系统的鲁棒稳定性。
4 算例分析
以某飞行器为例,建立全机结构动力学模型及非定常气动力计算模型,分别开展结构动特性计算和非定常气动力计算。典型结构模态及模态非定常压力分布如图6、图7所示。

图6 典型结构模态

图7 典型模态非定常压力分布
首先建立飞行器气动伺服弹性系统标称模型,在此基础上,考虑以下不确定因素影响:
a)燃料消耗带来的全机总质量、转动惯量的变化;
b)气动加热效应导致的材料弹性模量的下降,以全机广义刚度摄动表示;
c)舵机拟合参数(截止频率ωn、阻尼比ξ)的误差及分散度;
d)控制系统增益K1的摄动。
考虑如表1所示的两种参数摄动情况,开展飞行器控制系统三通道(俯仰、滚转以及偏航通道)交联耦合的鲁棒气动伺服弹性稳定性分析。

表1 参数摄动情况
分析结果µ值曲线如图8、图9所示。

图8 情况1的µ值曲线

图9 情况2的µ值曲线
根据µ方法鲁棒稳定性判据,在第1种参数摄动情况下,系统最大µ值小于1,系统鲁棒稳定;在第2种参数摄动情况下,系统最大µ值几乎等于1,系统鲁棒稳定性较差,极易发生气动伺服弹性失稳,在设计中应引起重视。
5 结束语
跨大气层飞行器气动伺服弹性系统模型建模涉及多个学科,包含多个子系统,建模复杂。此外,飞行环境变化大,飞行速度跨越亚、跨、超声速范围;气动热效应显著;由于燃料消耗的原因,系统的质量特性变化较大。以上因素不可避免地给气动伺服弹性系统建模带来系统误差和外界干扰。为保证安全飞行,有必要进行气动伺服弹性鲁棒稳定性分析。
对于线性系统,气动伺服弹性稳定性分析方法有Nyquist方法、最小奇异值法以及结构奇异值µ方法等。研究表明,相比其他方法,µ方法适用于控制通道间存在交联耦合的飞行器进行气动伺服弹性稳定性分析,且能考虑系统参数不确定性和多种不确定性摄动的影响,因而非常适合跨大气层飞行器,是一种很有前景的飞行器气动伺服弹性鲁棒稳定性分析方法。
[1]陈桂彬, 邹丛青, 杨超. 气动弹性设计基础[M]. 北京: 北京航空航天大学出版社, 2004.
[2]Richetts R H, Noll T E, Whitlow Jr. An overview of aeroelasticity studies for the national aero-space plane[R]. AIAA 93-1313-CP, 1993.
[3]惠俊鹏, 杨超. 考虑参数摄动的飞行器气动伺服弹性鲁棒稳定性分析研究[J]. 导弹与航天运载技术, 2015(6): 1-5.
[4]Spainin C V, Zeiler T A, Gibbons M D. Aeroelastic character of a national aerospace plane demonstrator concept[R]. AIAA 93-1314-CP, 1993.
[5]Changho N, Youdan K, Jeffrey B L. Active aeroelastic wing design for gust load alleviation and flutter suppression[R]. AIAA-97-1265-CP, 1997.
[6]吴志刚, 杨超. 气动伺服弹性系统不确定性建模与鲁棒稳定性[J]. 航空学报, 2003,24(4): 312-316.
[7]宋晨, 杨超, 吴志刚. 3种气动弹性状态空间建模方法的对比[J]. 航空学报, 2007,28(8): 81-86.
[8]Tiffang S H, Karpel M. Aeroservoelastic modeling and applications using minimum-state approximations of the unsteady aerodynamics[R]. AIAA paper 89-1188, 1989.
[9]Mukhopadhyay V. Flutter suppression control law design and testing for the active flexible wing[J]. Journal of Aircraft, 1995, 32(1): 45-51.
[10]Balas G J, Doyle J C, Glover K. MATLAB µ-analysis and synthesis toolbox user’s guide[M]. USA: The MathWorks Inc, 1998.
[11]Newsom J R, Mukhopadhyay V. A multiloop robust controller design study using singular value gradients[J]. Journal of Guidance, Control and Dynamics, 1985, 8(4): 514-519.
[12]Doyle J C. Structured uncertainty in control systems design[C]. USA: Proceedings of IEEE Conference on Decision and Control, 1985.
[13]Lind R, Brenner M. Analyzing aeroservoelastic stability margins using the µ-method[R]. AIAA-98-1895, 1998.
Research on Methodology of Aeroservo-elastic Stability Analysis for Trans-atmospheric Vehicle
Hui Jun-peng1,2, Yang Chao2
(1. R&D Center, China Academy of Launch Vehicle Technology, Beijing, 100076; 2. Beihang University, Beijing, 100191)
Using wing-body configuration and big lifting surface and control surface, trans-atmospheric vehicle usually has low overall structure stiffness and wide-band multi-way cross-linked flight control system, and must withstand complex flight environment and serve aerodynamic heating during reentry. Factors above may easily induce aeroservo-elastic stability problems. Due to external disturbance, vehicle model perturbation and coupling of control channels, robustic aeroservo-elastic stability analysis must be applied to trans-atmospheric vehicle. In this paper, motion equations of flexible flight vehicle are deduced by using Lagrangian method considering coupling between rigid-body modes and elastic vibration modes. State-space model of closed-loop aeroservo-elastic system is established based on rational function approximation of unsteady aerodynamics and modeling of servosystem and flight control system. Furthermore, nyquist criteria, the minimal singular value theory and the structured singular value analysis are studied for aeroservo-elastic stability analysis, and some conclusions are drawn consequently.
Trans-atmospheric vehicle; Aeroservo-elasticity; Stability; Structured singular value; µ-method
V411
A
1004-7182(2017)01-0042-06
10.7654/j.issn.1004-7182.20170111
2016-07-20;
2016-10-20;数字出版时间:2017-01-06;数字出版网址:www.cnki.net
惠俊鹏(1981-),男,高级工程师,主要研究方向为飞行器总体设计

