有限推力机动变轨能力包络快速计算分析

解永锋，周文勇，杜大程，陈 益，王传魁

（北京宇航系统工程研究所，北京，100076）

有限推力机动变轨能力包络快速计算分析

解永锋，周文勇，杜大程，陈 益，王传魁

（北京宇航系统工程研究所，北京，100076）

通过设计加权的组合性能指标函数，将机动变轨能力包络计算评估问题转化为一系列使组合性能指标最优的飞行任务规划问题求解，并采用求解精度高、收敛速度快的伪谱结点-非线性规划方法将存在多个推进-滑行段的最优任务规划问题离散转换并快速求解。算例仿真表明，采用该方法可以综合评估限定推进剂耗量、程序角速率限幅等约束下的机动变轨能力包络，给出满足可控性要求的最优飞行轨道，进而可以增强小推力长期在轨机动飞行器的多样化任务适应能力。

机动变轨；能力包络；任务规划；伪谱结点

0 引 言

为满足空间多样化任务需求，轨道机动飞行器在轨机动过程通常分为变轨任务规划和主动变轨实施两个阶段，在变轨任务规划阶段，需要根据飞行器当前飞行轨道以及目标轨道进行变轨策略规划，包括对发动机工作次数、点火时刻、主动段飞行程序角规划；在主动变轨实施阶段，需要根据规划方案，进行主动变轨前调姿，然后轨控发动机按要求工作，实现变轨机动。对于长期在轨采用有限推力的轨道机动飞行器而言，由于携带的推进剂有限，必须在综合评估其剩余机动变轨能力的基础上，根据任务目标，制定兼顾机动变轨时间和燃料耗量的变轨策略，以保障轨道机动飞行器的后续任务执行能力。

目前有关空间轨道转移优化的文献较多[1～4]，但大多是针对固定目标轨道的优化算法研究，通常采用简化的轨道动力学模型，不考虑程序角速率限幅和程序角限制，以燃料消耗最优作为性能指标函数，优化得到的飞行轨迹并未考虑工程可实现性，而优化算法亦不能用于真实飞行任务规划和变轨能力评估层面。本文以最优控制理论为基础，采用伪谱结点-非线性规划方法，通过引入伪控制量，将机动变轨能力包络计算评估问题转化为一系列使组合性能指标最优的机动变轨任务规划问题，规划得到的飞行轨道程序角平滑且可自动满足角速率限幅约束，具备工程可实现性。

1 空间轨道动力学描述

1.1 动力学模型

地心发射惯性坐标系下建立的空间飞行器的三自由度质点运动方程为

式中r,V为惯性位置和速度向量；g(r)为考虑 J2引力项摄动的重力加速度；T为发动机推力，与飞行器纵轴方向相同；vacT为最大真空推力幅值；η为发动机节流阀值，η＞0；spI为发动机比冲；m为飞行器质量；g0为海平面重力加速度； 1b为单位向量，表示纵轴方向，与俯仰及偏航程序角(,)φ ψ的对应关系为

1.2 飞行约束

机动变轨需满足的状态变量和控制量约束条件为

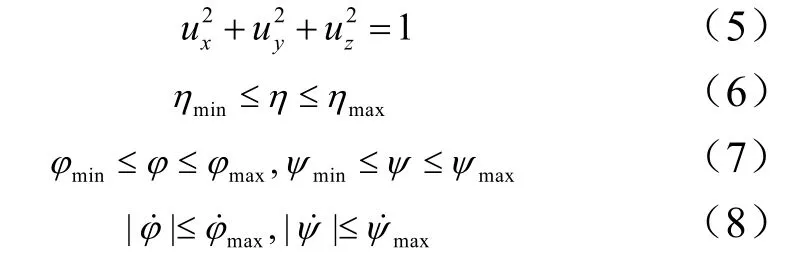
式中minmax,ηη为节流阀约束的上、下边界，若发动机为固定推力，ηmin=ηmax=1；φmin,φmax,ψmin,ψmax为俯仰、偏航程序角约束的上、下边界；,为程序角速率

限幅值。

2 伪谱最优控制

2.1 最优控制问题描述

针对空间轨道规划问题的特点，定义最优控制问题(B)为：a）寻求状态-控制函数对(x, u)∈RNx×RNu和可能未知的端点时刻τ0和τf；b）以最小化设定的性能指标函数；c）满足状态-控制变量约束、动态约束（状态方程约束）、轨道约束和端点约束等，表示为

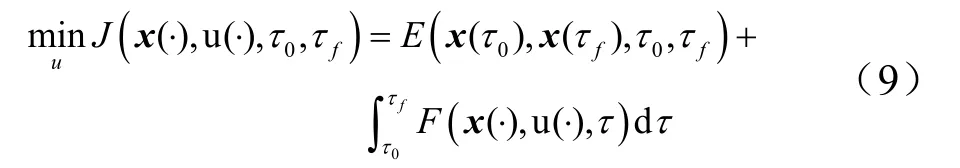
并且满足：

式中x为状态变量，x∈RNx；xL,xU分别为状态变量约束的上、下界；u为控制变量，u∈RNu；uL,uU分别为控制变量约束的上、下界；E为终端性能指标，；F，f为性能指标函数，函数中的拉格朗日项、状态方程右端项为，；h为状态-控制混合轨道约束，；hL,hU分别为轨道约束的上、下边界；e为端点约束，；uL,uU分别为端点约束的上、下边界。

2.2 伪谱最优控制问题转化

为达到节省燃料的目的，机动变轨可能以推进-滑行-推进的模式进行，对于这类多阶段并存在状态量、控制量不连续的最优控制问题，可采用伪谱结点法[5]进行处理，将最优控制问题转换为非线性规划问题，并利用成熟的非线性规划方法求解。

不失一般性，以两阶段最优控制问题为例，每一阶段的问题形式与2.1节问题()B相同。定义τe是中间时间点（伪谱结点），两段时间子区间分别为，则最优控制问题可以离散转化为

以及事件时间点 τ0,τe,τf，以满足如下约束：

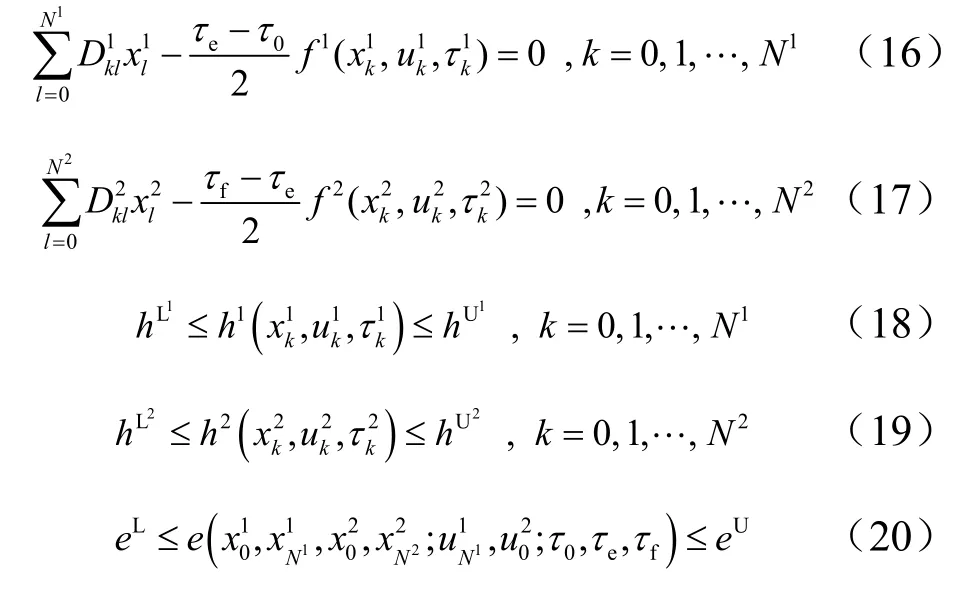
式中N1, N2为计算节点数；为(Ni+1)×(Ni+1)维微分矩阵，为N阶拉格朗日插值多项式，并最小化性能指标为

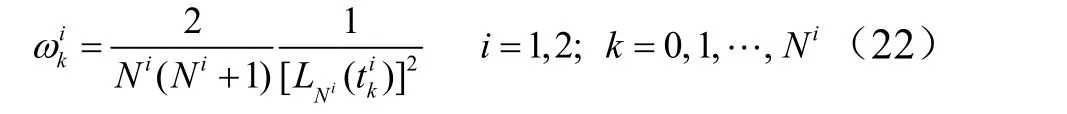
关于伪谱结点法的详细介绍可参考文献[5]，在此不再详述。

2.3 光滑控制生成

为保证控制量-俯仰及偏航程序角变化平滑，引入程序角的变化率作为伪控制量，而原控制量作为新的状态变量，扩展后的状态方程为

2.4 性能指标

若要衡量变轨机动对轨道面的改变能力，则可定义轨道倾角及升交点赤经的加权组合作为性能指标函数即：

式中w为权重因子，w∈[0,1]；if,Ωf分别为主动变轨段终端轨道倾角及升交点赤经。并限定发动机最大工作时间以表征所允许的最大推进剂耗量。轨道倾角及升交点赤经同时调整的能力包络计算可以转化为求解给定终端飞行约束和路径约束，并采用考虑J2引力项摄动的轨道动力学方程，以最优化上述组合性能指标的最优控制问题。

对于终端轨道固定的机动变轨任务，为使燃料消耗最优，可采用如下性能指标函数：

3 算例分析

3.1 异面机动轨道规划

假设在轨机动飞行器初始质量1 860 kg、主发动机推力2 000 N、比冲为290.5 s，推进剂加注量700 kg，飞行器初始及终端轨道约束见表1。俯仰及偏航程序角限幅值取1.5（°）/s。以燃料消耗最优作为性能指标，分别基于伪谱最优控制方法规划一次变轨和两次变轨模式的飞行轨道。

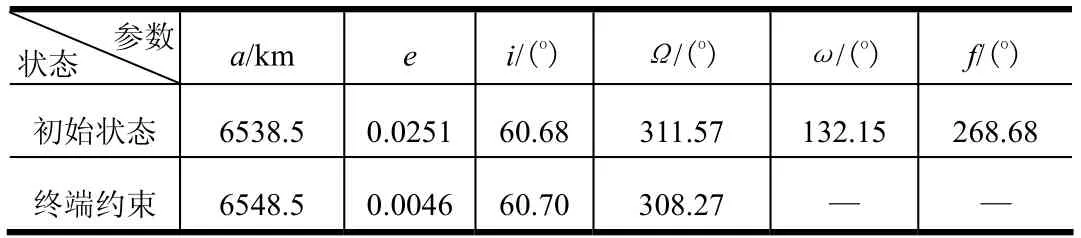
表1 机动变轨段端点约束

3.1.1 一次变轨模式

图1 俯仰程序角及其变化率

图2 偏航程序角及其变化率

飞行轨道参数变化曲线如图3所示。

图3 轨道倾角及升交点赤经

由图3可以看出，一次变轨同时调整俯仰及偏航程序角，可以达到所要求的多终端约束，进入目标椭圆轨道。通过对图 3的分析可知，由于所需修正的升交点赤经较大且轨道倾角修正量很小，而主发动机点火时刻轨道纬度幅角约为40.82°，由轨道摄动理论可知，对升交点赤经修正的同时必然会不可避免地造成轨道倾角的改变，为达到所要求的目标修正量，必须在提升近地点高度的同时，拉大当前轨道倾角与目标值的偏差，然后再实现轨道倾角与赤经的同时修正，这也是造成推进剂耗量较大的主要原因。

3.1.2 两次变轨模式

采用前面所述伪谱结点法，将两次主动段工作时间及滑行时间作为优化变量，在两次主动段之间加入滑行段，其中第1主动段主要用于改变半长轴和偏心率，将轨道拉起，然后经过一段时间的滑行，待纬度幅角满足要求后，发动机再次工作，对轨道面进行修正。采用两次变轨模式，可显著减小推进剂耗量，主发动机两次工作时间之和为340.5 s，推进剂消耗239.1 kg。

两次变轨段的飞行程序角见图4、图5，与一次变轨模式相比，程序角变化范围较小，更易于控制实现。

图4 第1主动段飞行程序角

图5 第2主动段飞行程序角

与之对应的轨道倾角及升交点赤经变化见图6、图7，与一次变轨模式相比，轨道倾角变化幅角较小，且升交点赤经逐步向目标值靠近，不会出现先增大再减小的情况。

图6 轨道倾角

图7 升交点赤经

3.2 轨道修正能力包络

采用2.4节定义的性能指标函数，采用的初始及终端约束见表 2，计算经过一次机动变轨进入155 km× 200 km 的椭圆轨道，并同时调整轨道倾角及升交点赤经能力包络。

表2 机动变轨段端点约束

因推进剂加注量为700 kg，考虑主发动机最大允许工作时间tbmax在200～800 s之间变化，计算得到的异面变轨机动能力包络曲线如图8所示。不同线形表示不同的允许主发动机工作时间，所组成的闭合区域表示可以达到的轨道机动量，且所需主发动机工作时间不超过tbmax，由图8可见所能实现的轨道可机动区域随 tbmax的减小而缩小；在轨道倾角改变量|iΔ|较小的情况下，主发动机工作时间（推进剂耗量）随升交点赤经改变量|ΩΔ|的增大而快速增大。图中A点表示表 1所列的主发动机点火时刻目标轨道与飞行器的轨道倾角及升交点赤经之差，靠近tbmax=600 s闭合区域边界线，在tbmax=700 s闭合区域内，与优化计算得到的变轨时间相吻合。

图8 异面变轨能力包络

4 结 论

采用基于伪谱最优控制的轨道规划策略，可以快速评估限定推进剂耗量、程序角速率限幅等多重约束下的机动变轨能力包络，并给出满足工程可控性要求的一次或多次变轨最优飞行轨道，进而增强有限推力长期在轨轨道机动飞行器的多样化任务适应能力。

[1]Yue X, Yang Y, Geng Z. Indirect optimization for finite-thrust time-optimal orbital maneuver[J]. Journal of Guidance Control and Dynamics, 2010, 33(2): 628-634.

[2]王常虹, 曲耀斌, 陆智俊, 等. 航天器有限推力轨道转移的轨迹优化方法[J]. 西南交通大学学报, 2013, 48(2): 390-394.

[3]郑昌, 文赵伟. 基于进化计算的轨道转移时间-能量优化方法[J]. 计算机工程与设计, 2008, 29(3): 735-737.

[4]刘峰. 有限推力轨道转移优化方法与应用研究[D]. 长沙: 国防科技大学, 2009.

[5]Ross I M, Fahroo F. Discrete verification of necessary conditions for switched nonlinear optimal control systems[C]. Boston: Massachusetts, 2004.

Rapid Computation and Analysis of Finite Thrust Maneuver Capability

Xie Yong-feng, Zhou Wen-yong, Du Da-cheng, Chen Yi, Wang Chuan-kui
(Beijing Institute of Astronautical Systems Engineering, Beijing, 100076)

Evaluating of maneuver capability envelope is transformed into a serial optimal flight mission planning problems through designing weighted combined cost functions, and the optimal mission planning problem that includes multi-thrust-coast phases can be transformed and solved rapidly by high precision pseudospectral knotting- nonlinear programming method. Numerical simulation shows that this method can generate controllable optimal flight trajectories while evaluating the integrated maneuver capability under various constraints including fuel consume and control angle rate limit, which will enhance the mission adaptability of finite thrust long-term in orbit maneuver vehicles.

Orbit maneuver; Capability envelop; Mission planning; Pseudospectral knotting

V412.4

A

1004-7182(2017)01-0014-04

10.7654/j.issn.1004-7182.20170104

2015-09-16；

2015-11-17

解永锋（1984-），男，博士，工程师，主要研究方向为飞行器动力学控制