基于ARMA-NExT的飞行器工作模态辨识技术研究
王 亮,蔡毅鹏,朱 辰,廖选平,,祝学军
(1. 中国运载火箭技术研究院,北京,100076;2. 国防科技大学航天科学与工程学院,长沙,410073)
基于ARMA-NExT的飞行器工作模态辨识技术研究
王 亮1,蔡毅鹏1,朱 辰1,廖选平1,2,祝学军1
(1. 中国运载火箭技术研究院,北京,100076;2. 国防科技大学航天科学与工程学院,长沙,410073)
基于飞行实测遥测数据,研究了使用工作模态辨识方法辨识飞行器系统的模态参数。详细介绍了ARMA-NExT工作模态辨识理论基础,梳理了模态辨识的关键步骤和实施方法,最后通过两个算例研究了工作模态辨识。结果表明:第 1个算例是针对某一小段时间的遥测数据,辨识系统的模态参数,包括模态频率、阻尼比和振型;第 2个算例针对较长时间的遥测数据,辨识系统的模态频率随时间变化的规律。
模态辨识;ARMA;NExT;工作模态
0 引 言
航天工程中,为了进行载荷计算、姿态控制设计、动响应分析,需要精确预示战术导弹的结构动力学特性。在设计时,一般采用理论计算和模态试验相结合的方法,先使用理论计算,再通过有限状态的模态试验结果对理论模型进行修正,最后使用修正的理论模型计算各状态下的模态特性。而地面试验无法完全模拟飞行的状态,如外部的气动力和发动机的推力等。因此,基于遥测数据,对飞行过程中的结构模态参数进行辨识,对设计参数进行验证显得非常重要。
飞行器在飞行过程中的外部环境激励无法精确测量,只能获得某些部位的动力学响应信号,因此可以采用环境激励模态辨识技术。环境激励模态辨识技术是将互相关函数同传统时域模态分析法相结合的方法,将各部位结构动力学响应之间的互相关函数代替传统时域模态分析法中的自由振动衰减响应或脉冲响应函数。因此该方法不需要测量激励信号,而仅依靠各通道的时域响应数据进行系统的模态辨识。
环境激励模态辨识技术的使用步骤为:a)进行结构动力学响应信号的采样;b)对采样数据进行自相关和互相关计算,在进行多个测点的模态参数识别时,需要选取某个测点做参考点(一般选取响应较小的测点做参考点),计算其它测点与该参考点的互相关函数;c)将计算出来的互相关函数作为输入,利用时域模态辨识方法如ITD法、STD法、复指数法和ARMA模型时序法以及ERA法等模态参数辨识方法进行参数识别。目前,该方法已广泛应用于桥梁、高层建筑、汽轮机、飞机和汽车等的模态参数辨识[1~10]。
综上所述,针对飞行器飞行条件下的结构动力学参数辨识问题,本文基于遥测振动数据,使用ARMA-NExT模态辨识方法研究了导弹飞行过程中的模态参数,并利用环境激励法跟踪飞行器飞行过程中的工作模态。
1 ARMA模态辨识技术
ARMA模型时间序列分析法简称为时序分析法,是一种利用参数模型对有序随机振动响应数据进行处理,从而进行模态参数识别的方法。N个自由度的线性系统激励与响应之间的关系可用高阶微分方程来描述,在离散时间域内,该微分方程变成由一系列不同时刻的时间序列表示的差分方程,即ARMA时序模型方程[10]:
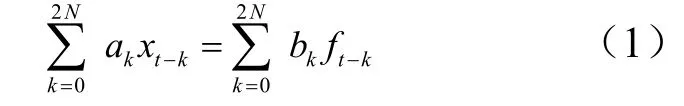
式中ka为待识别的自回归系数;kb为滑动均值系数;ft为白噪声激励。
式(1)表示响应数据序列xt与历史值xt-k的关系,其中等式的左边称为自回归差分多项式,即AR模型,右边称为滑动平均差分多项式,即MA模型。2N为自回归模型和滑动均值模型的阶次。
当求得自回归系数ak和滑动均值系数bk后,可以通过ARMA模型传递函数的表达式计算系统的模态参数,ARMA模型的传递函数为

式中z为传递函数自变量。
用高次代数方程求解方法计算分母多项式方程的根即:

求解得到的根为传递函数的极点,与系统的模态频率ωk和阻尼比ξk的关系为

并且可求得模态频率ωk和阻尼比ξk,即:

为计算模态振型,需要先求出留数。设q点处激励p点响应的传递函数Hpq(s)的第是阶留数为Akpq,可用下式计算留数:
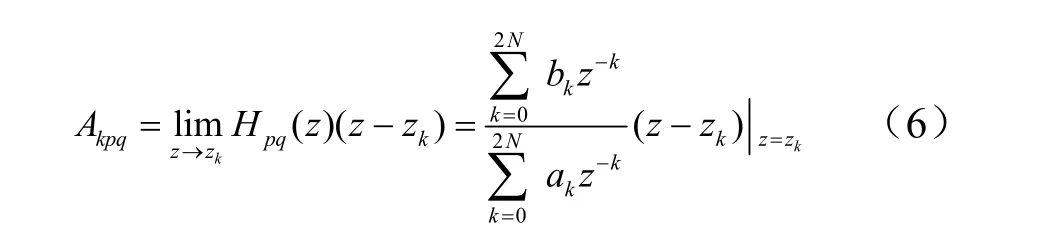
振型向量可以通过对一系列响应测点求出的留数处理得到。对于一个有 n个响应测点的结构,首先需要从 n个对应同一阶模态的留数中找出绝对值最大的测点,假设该点是测点m,对应第k阶模态的归一化复振型向量可由下式求出:

2 算例研究
以下通过两个算例研究了工作模态辨识的方法,算例说明如下:
a)算例一:根据某段遥测数据辨识其模态参数,如模态频率、阻尼比和振型;
b)算例二:对时间较长的遥测数据辨识其低阶模态频率随时间的变化关系。
2.1 算例1——模态参数辨识
图1给出了针对选定的一段遥测数据模态参数辨识的计算流程。先对遥测数据进行预处理,去除野点和中值,再使用带通滤波器筛选出待辨识频带的信号,对信号进行重采样,缩短信号长度,最后通过模态辨识方法进行模态辨识,得到飞行器当前时段的工作模态参数。

图1 计算流程
选择一段1.5 s长度的信号,进行预处理,由于原信号采样频率为5 120 Hz,待辨识频带为200 Hz以内,因此选择带通滤波器频带选择为20~200 Hz进行滤波,并对信号进行重采样,信号处理前后对比如图2所示。

图2 参考点信号滤波处理前后时域数据对比
典型通道响应信号处理后的功率谱密度曲线和时频分析结果如图3和图4所示。可以看出,谐振峰位置在45 Hz、88 Hz和120 Hz处。

图3 处理前后参考点信号的功率谱密度曲线对比
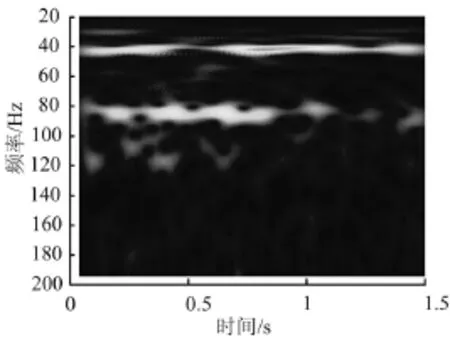
图4 时频分析结果
使用ARMA-NExT模态辨识方法对各通道响应信号进行拟合,典型测点如参考点原点自由衰减信号拟合结果如图5所示。从图5看出:对于参考点以及与参考点较近的测点的自由衰减信号拟合精度较好,但对于远离参考点的测点,其拟合精度较差。
根据以上对各信号的拟合结果,辨识了前 4阶的模态振型和频率辨识结果如图6和表1所示。

图5 参考点原点自由衰减信号拟合

图6 振型辨识结果

表1 模态频率辨识结果
从以上分析结果可以发现:
a)模态频率辨识结果与功率谱密度分析结果的谐振峰值位置基本一致;
b)模态振型反应了自由梁的振型特征,但由于测点数过少,因此形态连续性及完整性较差。
2.2 算例2——随时间工作模态辨识
图7给出了工作模态辨识的实现步骤。首先选择时间间隔,将原始遥测数据分割为n段数据,分别对各段数据进行数据预处理,消除趋势项和野点;然后一方面对信号进行功率谱密度分析,根据分析结果选择制定各阶模态的大概区域位置,另一方面对信号使用随机减量技术将其处理为自由衰减数据,再使用ARMA模型拟合数据,配合指定各阶模态的大概位置获得模态频率值;最后将各时间段模态辨识结果画图得到各阶模态频率随时间的变化曲线。

图7 工作模态辨识实现框图
以下通过算例研究模态辨识的方法。这里将遥测数据分成了8段,分别对各段进行功率谱密度曲线使用图7给出的方法进行模态辨识后,得到各阶模态随时间的变化如图8所示。
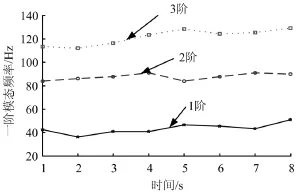
图8 工作模态时间曲线
从以上分析结果可以发现:
a)发动机装药逐渐消耗,飞行器整体质量减轻,因此各阶模态频率升高,辨识结果与规律一致;
b)遥测数据,个别时刻的辨识结果有跳变。
由于各振动测点比较侧重仪器环境的测量,对于模态辨识信息量以及测点优化布置未过多考虑,是造成辨识精度较差的原因。
3 结 论
基于飞行遥测实测数据,本文研究了使用工作模态辨识飞行器在飞行状态下的模态参数。通过两个算例研究了工作模态辨识。
研究结果表明辨识结果可以反映导弹在空中飞行状态下的真实模态特性,其中模态频率可反映飞行器实际使用过程中模态变化规律,但其连续性受测点数据品质影响较大,另外模态振型的连续性及完整性受测点数目和分布影响较大。
[1]李惠斌. 大型工程结构模态参数识别技术[M]. 北京: 北京理工大学出版社, 2007.
[2]傅志方, 华宏星. 模态分析理论与应用[M]. 上海: 上海交通大学出版社, 2000.
[3]罗鹏飞, 张文明. 随机信号分析与处理[M]. 北京: 清华大学出版社, 2006.
[4]Peeters B, De Roeck G, et al. Stochastic subspace techniques applied to paremeter identification of civil engineering structures[C]. Lyon: Proceeding of New Advances in Modal Synthesis of Large Structures: Nonlinear, Damped and Nondeterministic Cases, 1995.
[5]Ibrahim S R. Efficient random decrement computation for Identification of Ambient[C]. Florida: Responses, Proceeding of 19th IMAC, 2001.
[6]Abdelgham M, Goursat M, et al. On-Line modal monitoring of aircraft structures under unknow excitation[J]. Mechanical Systems and Signal Processing, 1999, 13(6): 839-853.
[7]Guid D R, et al. Benchmark study on system identification through ambient vibration measurements[C]. San Antonio: 18th IMAC, 2000.
[8]Rune B, et al.Modal Identification from ambient responses using Frequency domain decomposition[C]. San Antonio: 18th IMAC, 2000.
[9]Bonato B, Ceraavolo R, Stefano A D. Use of cross-time-frequency estimators for structural identification in non-Stationary conditions and under unknowm excitation[J]. Journal of Sound and Vibration, 2000, 237(5): 775-791.
[10]王亮, 张妍, 周晓丽, 商霖, 朱辰, 蔡毅鹏. 基于ARMA-NExT和稳定图方法的飞行器工作模态指示研究[J]. 动力学与控制, 2016, 14(3): 258-262.
Operational Mode Identification of the Aircraft Based on ARMA-NExT
Wang Liang1, Cai Yi-peng1, Zhu Chen1, Liao Xuan-ping12, Zhu Xue-jun1
(1. China Academy of Launch Vehicle Technology, Beijing, 100076; 2. College of Aerospace Science and Engineering; National University of Defense Technology, Changsha, 410073)
Based on the telemetry data, the operational mode identification of the Aircraft is investigated under ambient excitation based on ARMA-NExT method. Firstly, the theory of the ARMA-NExT method is introduced. Secondly, the strategy decomposition and implementation are put forward. At last, two examples are studied, one is aim at the operational mode identification for a period of time, include model frequency, damping and shape, and the other is to derive the variation of the model frequency with time.
Mode identification; ARMA; NExT; Operational mode
V415
A
1004-7182(2017)01-0018-04
10.7654/j.issn.1004-7182.20170105
2015-11-10;
2015-12-20
国家重点实验室2015年开放课题(MCMS-0115G01);国防技术基础科研项目(JSZL2015203B002)
王 亮 (1985-),男,博士,高级工程师,主要研究方向为导弹载荷与环境设计

