声速测定实验中超声换能器的非线性行为

杨睿智,李熹辰，蔡昊君，杨胡江，肖井华

(北京邮电大学 理学院，北京 100876)

声速测定实验中超声换能器的非线性行为

杨睿智,李熹辰，蔡昊君，杨胡江，肖井华

(北京邮电大学 理学院，北京 100876)

在声速测定实验中，通过频谱分析、幅频特性曲线和相图，研究了发射和接收超声换能器在不同频率的驱动下从线性状态转变成非线性状态的过程，观察了超声换能器表现出的准周期态、倍频现象、磁滞和双稳态现象等丰富的动力学行为.

超声换能器；非线性；声速

声速测定实验是大学物理实验中的经典实验项目[1-2]，通常采用2个超声换能器来产生和接收超声波. 超声换能器的主要部件是压电陶瓷，压电陶瓷利用压电效应和逆压电效应[3]将电信号转换成超声波，也能将超声波转换成电信号. 压电效应应用非常广泛，比如表面分析、导航和无损检测等[4-6].

1 超声换能器的非线性行为

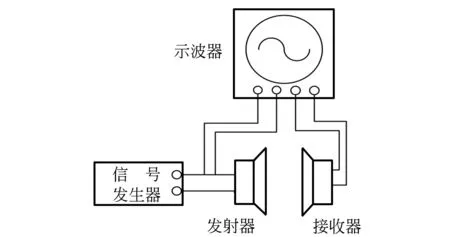
图1 声速测定实验的装置示意图

图1给出了声速测定实验的装置示意图[7-8]，包括示波器(Tektronix DPO3032)、信号发生器(SUING TFG1005)和2个超声换能器(发送器和接收器，其谐振频率为f=38.00 kHz). 发送器同时连接信号发生器和示波器，接收器的输出信号直接连接到示波器上. 通常，发送器能够将驱动的正弦信号(38.00 kHz)转换成同频率的超声波，当发送器和接收器之间的距离恰好是声波半波长的整数倍时，接收器的声压达到最大. 此时，接收信号幅度达到最大值，此位置称为驻波的节点. 测量相邻2个驻波节点的距离，可以计算出声波的波长λ. 由公式[2]v=λf，可以得到空气中的声速v.

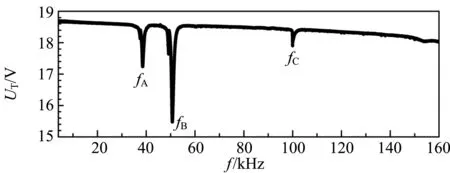
(a)发送器

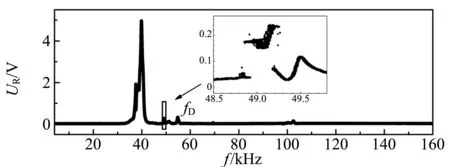
(b)接收器图2 发送器和接收器的幅频特性曲线

在实验中，改变驱动频率，发现换能器不只有1个谐振频率. 图2给出了发送器和接收器的幅频特性曲线. 图2中UT和UR分别是发送器和接收器上信号的峰峰值. 驱动信号是峰峰值20 V的正弦信号，信号频率可在0～160 kHz之间连续调节. 上述曲线是用数据采集卡和LabVIEW程序自动测量频率和信号幅度得到的.

从图2中可以看出，曲线上有4个共振峰(fA=38 kHz,fB=49 kHz,fC=100 kHz,fD=54 kHz). 由此可见，换能器在不同频率的驱动下必将表现出丰富的动力学行为，如共振频率移动[9]、信号波形畸变和磁滞现象[10-11]，甚至能够观察到倍频和混沌现象[12]. 这些非线性效应在超声的工业和测量应用方面[13]可能会带来相当广泛的影响，尤其是有害的影响. 因此，揭示这些现象的本质和探索更多的现象，如准周期和倍频现象，显得尤为重要.

由于实验现象非常丰富，本文主要讨论驱动频率在图2(a)中的fB附近. 在这个区域已经观察到了一系列非线性现象，如倍频现象、准周期态和磁滞现象等. 这些现象并非特例，而是这类换能器的共性.

声速测定实验中需要给发送器施加正弦波(38.00 kHz, 峰峰值20 V). 此时，发送器和接收器都工作在线性区，能够将电信号转换成同频率的超声波，也能将超声波转换成同频率的电信号. 因此，在接收器上能够收到3.6 V的正弦波信号，如图3(a)所示. 然而，当驱动频率为49.00 kHz(fB)时，接收器上的信号(下方的绿色波形)明显失去了稳定，在输入信号稳定不变的情况下，输出信号振幅明显变化，有不稳定的包络(220 mV)，如图3(b)所示. 同时，还能够听到发送器此时会发出频率很高的声音，这些声音的波形显示在图3(d)中. 继续增加驱动频率至49.39 kHz，接收信号出现稳定的波形，但已不是正弦波，而是类似倍频现象，在驱动信号变化1个周期内，接收信号2次达到极大值，如图3(c)所示.

(a)38.00 kHz

(b)49.00 kHz

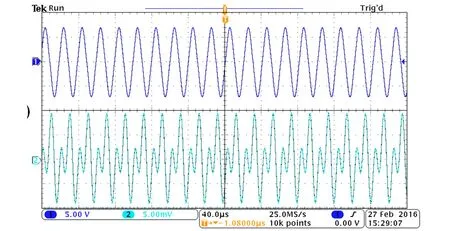
(c)49.39 kHz

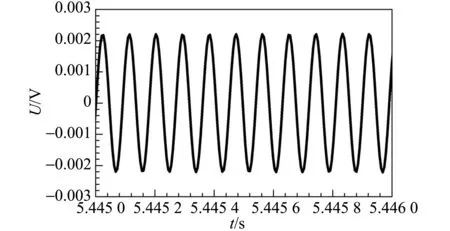
(d)用麦克接收的发送器发出声音的波形图3 不同驱动频率下示波器显示的发送器(上方的蓝色波形)和接收器(下方的绿色波形)上的电信号

2 实验结果分析

为了更好地理解换能器的这些非线性行为，用数据采集装置测量了输入和输出信号的幅频特性曲线，并仔细分析了这些信号的频谱. 数据采集装置包括数据采集卡(NI PCI-6110及其接线端子BNC-2110)、计算机及自编的LabVIEW程序. 通过这些手段，可以看到丰富的非线性动力学行为，如倍频现象、磁滞现象以及多态共存、准周期信号和新频率的产生.

2.1 频谱分析

从图3可以看出，发射信号变化不大，信息量很少，因此主要研究接收信号的频谱特性. 首先分析了图3(a)中的接收信号的频谱，见图4(a). 可以看出，图中除了少量噪声外，仅有单一频率信号(38.00 kHz)，这是简单的正弦波. 与此不同的是驱动频率为49.00 kHz时的接收信号[如图4(b)]，其频谱中除了驱动频率外，还含有很强的38.02 kHz信号，以及多个其他频率成分(59.98 kHz, 98.00 kHz). 与此同时，发送器发出的声音频谱也显示在图4(d)中，可看到简单的正弦波，频率为fs=11.05 kHz. 当驱动频率达到49.39 kHz时的接收信号[见图4(c)]，频谱中主要包括2个频率成分，49.39 kHz和98.78 kHz，且后一个频率刚好是前一个的2倍，与图3(c)中的倍频现象非常吻合.

(a)f=38.00 kHz

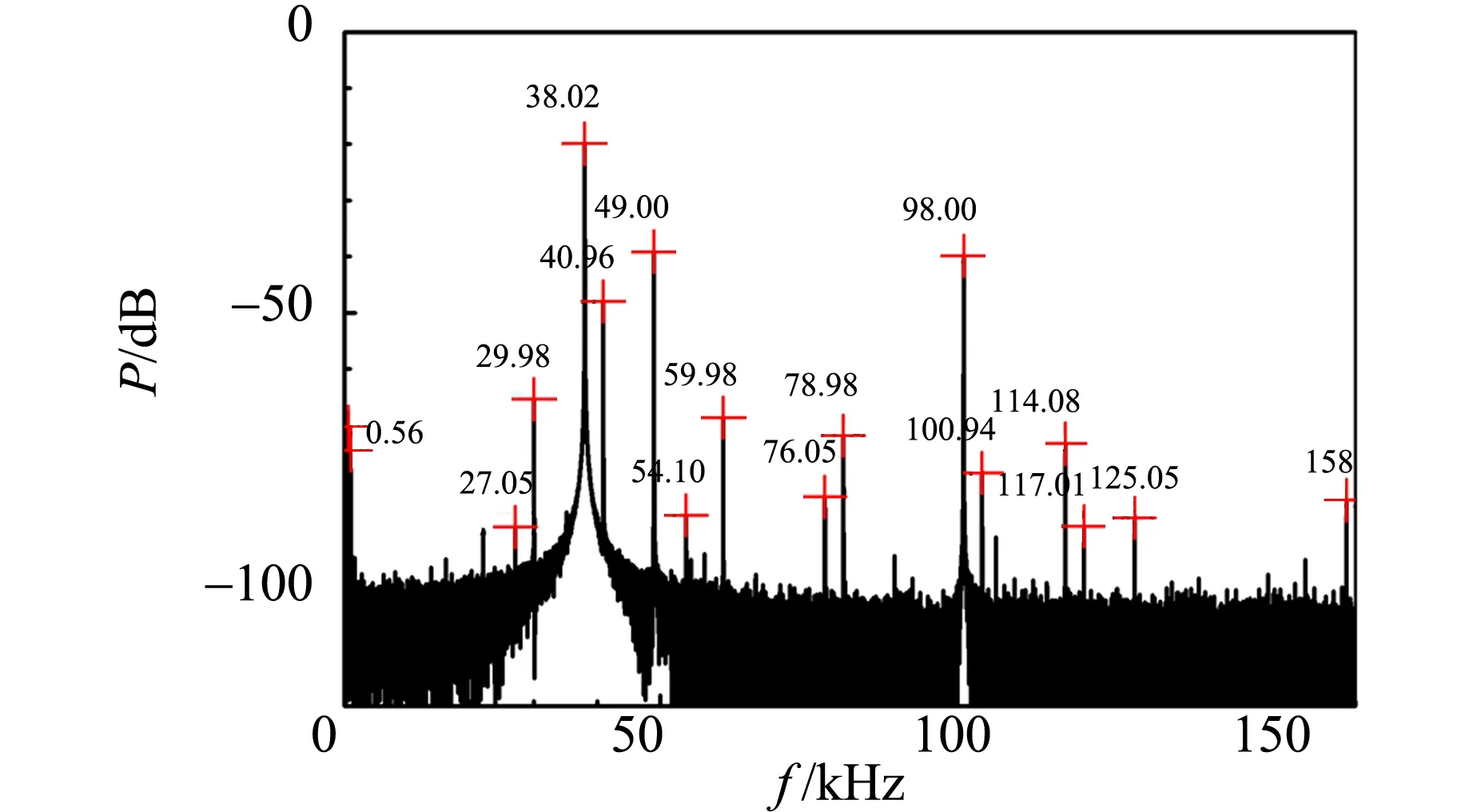
(b)f=49.00 kHz

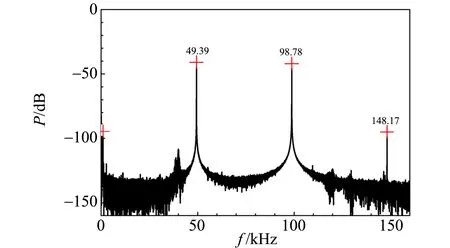
(c)f=49.39 kHz

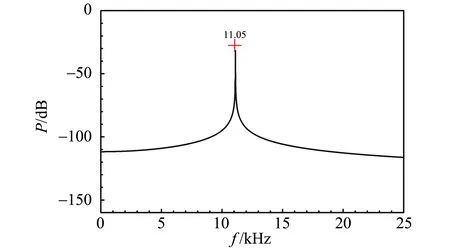
(d)发送器发出的声音频谱图4 图3中接收器上信号及声音的频谱图

分析图4(b)中各频率成分的关系，可以发现准周期信号的特征[14-15]. 这些信号都是驱动频率f1(49.00 kHz)和其他2个频率f2(40.96 kHz)和f3(38.02 kHz)的组合，fmnl=mf1+nf2+lf3，m，n和l都是整数. 如38.03 kHz就是f001，其他频率详见表1.

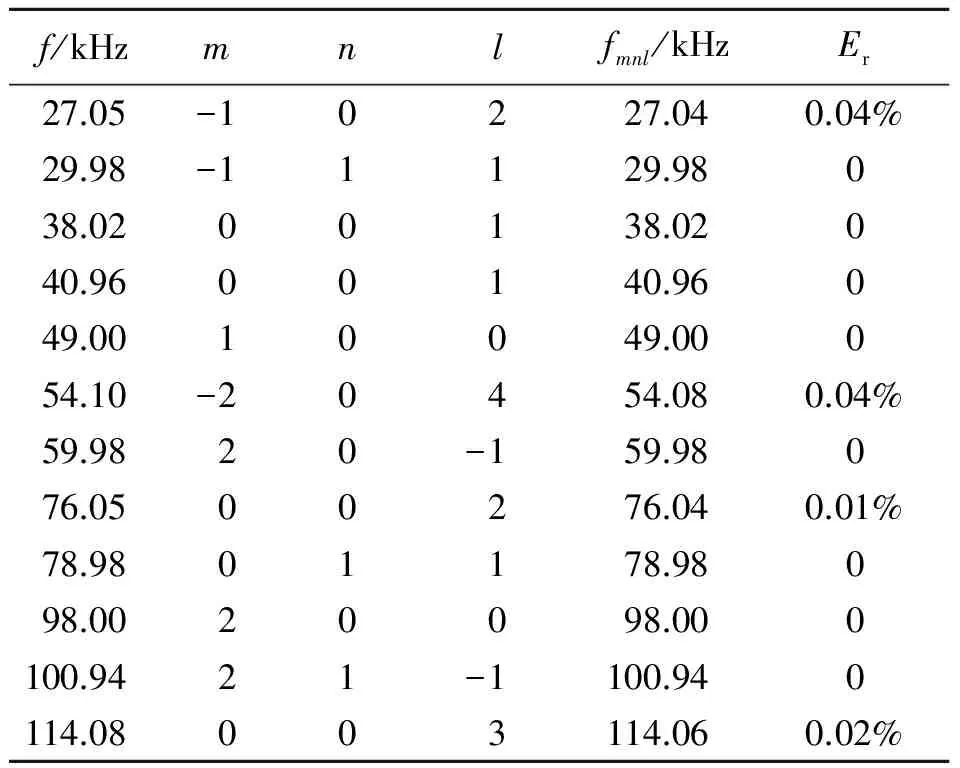
表1 图4(b)中各频率成分的关系

所有这些现象都说明，在频率fB附近，换能器有很强的非线性性质. 此时，在单一频率的驱动下，换能器能够产生多个频率成分，其中1个频率fs=f10-1=11.05 kHz在人耳能听到的范围内，这些频率最终混合成看到的准周期信号.

2.2 幅频特性分析

分岔过程是非线性领域重要的动力学现象，能够展现系统的特征和参量. 为了清晰地表现接收信号的分岔过程，预想通过fB附近(48.40～50.00 kHz)的幅频特性曲线来实现. 但是，在同一驱动频率下，接收信号并不稳定，因此不能直接测量其幅度，通过编程，采集此时的不稳定信号，并连续记录接收信号的极大值，将这些极大值都显示在幅频特性曲线上，如图5所示. 同时，改变驱动信号的电压，这些幅频特性曲线也都显示在图5中. 从图5可以看出，在48.50 kHz附近，接收信号为稳定信号，因此所有的极大值都几乎相等. 但在49.00 kHz附近，接收信号不稳定. 由于显示的区间较大，图3(c)中的倍频现象不明显，但在图6(b)中可清晰地看到49.39 kHz附近的2个峰值.

图5虚线连接的是不同电压下幅频特性曲线的峰值，不同驱动电压下的最大值不在同一频率，这一现象与P. A. Nicols的模拟工作吻合[16].

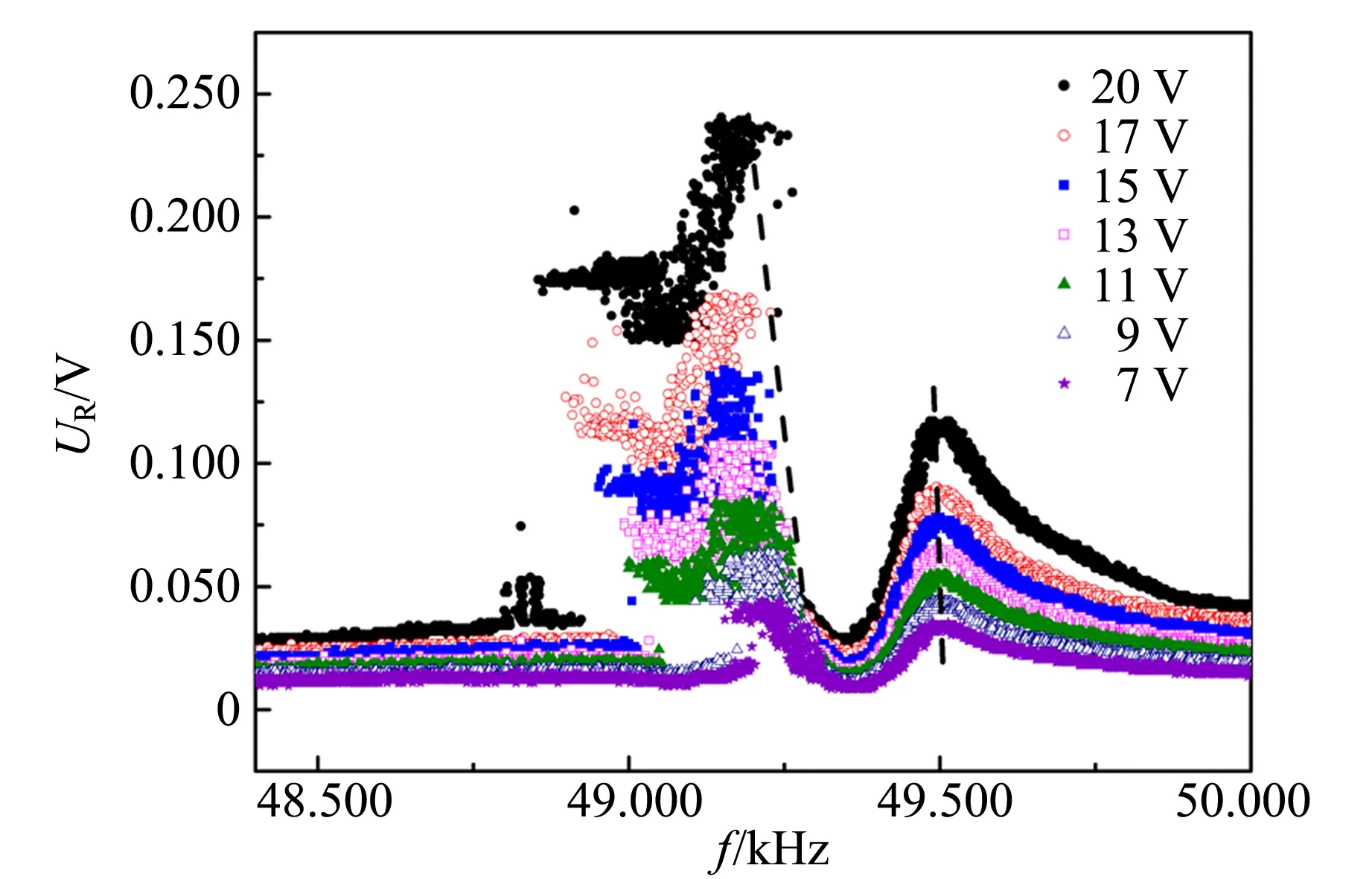
图5 不同驱动电压下的幅频特性曲线

2.3 磁滞现象

对于具有双稳态的系统来说，系统的最终状态与其初始状态有关. 一般认为，2种稳定状态之间的跳跃是由于1种状态的失稳. 为了更好地显示这种现象，重新采集了发送器和接收器的幅频特性曲线.

先将驱动频率设置为47.00 kHz，每0.1 s增大0.01 kHz，直至54.00 kHz，用同样的方式减小频率至47.00 kHz，实验结果如图6所示. 由于主要关心接收信号有倍频和磁滞现象的区域，因此图6(b)只显示了48.40～49.50 kHz范围内的信号. 从图6(a)中可以看出，频率增加和减小时，发送器的幅频特性曲线明显不同. 同样，从图6(b)中可以看出，频率逐渐减小时的接收信号不稳定的区间明显比频率增加时的范围大. 因此，频率在[48.63, 48.87] kHz内时，系统具有双稳态. 其实，频率在[48.63, 48.87] kHz内系统也具有双稳态、准周期态和倍频态双稳，这2种状态的波形图和相图如图7所示. 驱动频率同为49.13 kHz，图7(a)是驱动频率减小至49.13 kHz时的波形图τ=0.000 5 s，图7(c)是它的相图，可以明显看出，系统处于倍频状态. 图7(b)和(d)是驱动频率增大时的情况τ=0.000 1 s，系统处于准周期态.

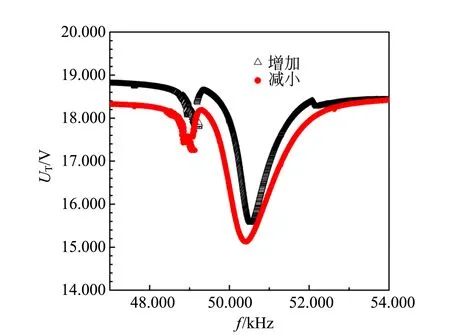
(a)发送器

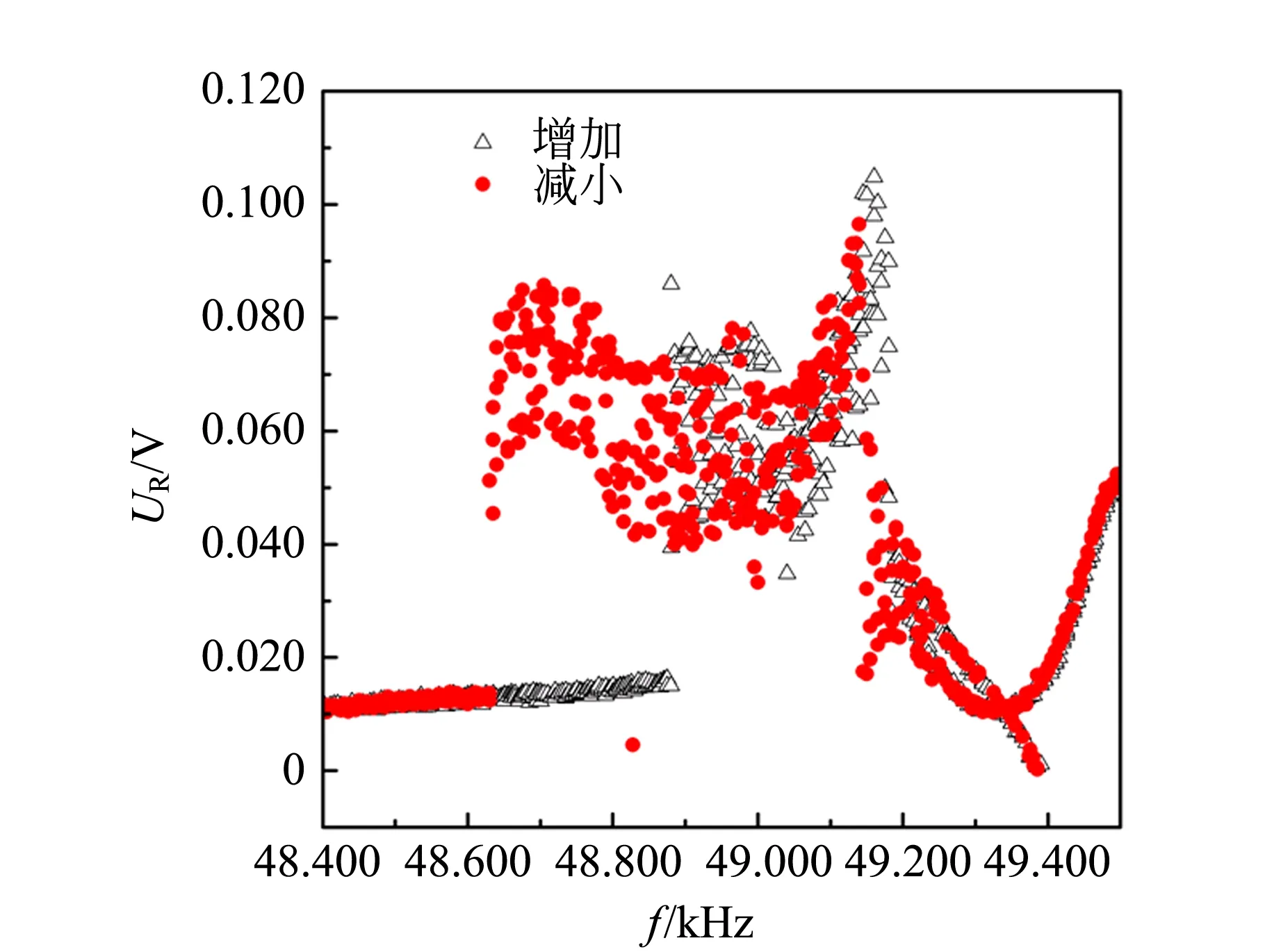
(b)接收器 图6 发送和接收换能器非线性区域的幅频特性曲线和磁滞现象

(a)τ=0.000 5 s时的波形图

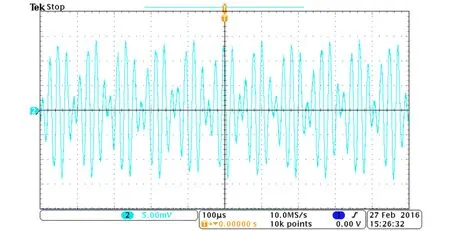
(b)τ=0.000 1 s时的波形图

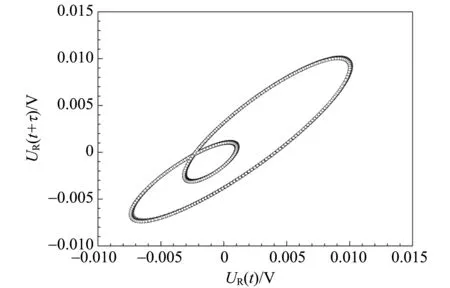
(c)τ=0.000 5 s时的相图

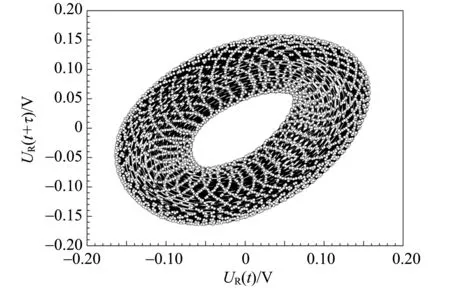
(d)τ=0.000 1 s时的相图图7 准周期和倍频双稳态的波形图和相图

3 结束语

用大学物理实验中常见的器件超声换能器，在幅频特性曲线、频谱分析和相图的帮助下，研究了换能器从线性状态转变到非线性状态的过程. 在此过程中观察到了丰富的非线性动力学行为，如准周期态、倍频态、磁滞和双态共存现象. 本文利用面向广大工科学生开设的大学物理实验装置，从偶然发现的接收信号不稳定现象出发，引导学生逐步深入研究探索，并最终揭示其物理机制，将创新教育融入课堂教学.

[1] Bohn D A. Environmental effects on the speed of sound [J]. J. Audio Eng. Soc.， 2012, 36(4):223-231.

[2] Yang Hujiang, Zhao Xiaohong, Wang Xin, et al. An undergraduate experiment for the measurement of the speed of sound in air: phenomena and discussion[J]. Eur. J. Phys., 2012,33(5):1197-1206.

[3] 田玉仙，李绍蓉，陈丹，等. 驻波法之声压极小值测声速研究[J]. 物理实验，2014,34(8):38-41.

[4] 赵西梅，李向亭，周红，等. 超声波声速测量的拓展实验[J]. 物理实验，2014,34(12):33-35.

[5] Gautschi G. Piezoelectric sensorics: force, strain, pressure, acceleration and acoustic emission sensors, materials and amplifiers [J]. Sensor Review, 2002,22(4):363-364.

[6] Thaisiam W, Laithong T, Meekhun S, et al. Echosonography with proximity sensors [J]. European Journal of Physics, 2013,34(2):415-420.

[7] Boser B E, Przybyla R J, Horsley D A, et al. Ultrasonic transducers for navigation [J]. Proceedings of Meetings on Acoustics, 2013,19(5):3499.

[8] Demirli R, Saniie J. Model-based estimation of ultrasonic echoes part II: nondestructive evaluation applications [J]. IEEE Transactions on Ultrasonics Ferroelectrics & Frequency Control, 2001,48(3):803-811.

[9] Aurelle N, Guyomar D, Richard C, et al. Nonlinear behavior of an ultrasonic transducer [J]. Ultrasonics, 1996,34(2/5):187-191.

[10] Neiss S, Goldschmidtboeing F, Kroener M, et al. Analytical model for nonlinear piezoelectric energy harvesting devices [J]. Smart Materials & Structures, 2014,23(10):105031.

[11] Gael S, Hiroki K, Daniel G, et al. Simulation of a Duffing oscillator for broad band piezoelectric energy harvesting [J]. Smart Materials & Structures, 2011,20(7):75022-75038.

[12] Mathieson A, Cardoni A, Cerisol N, et al. Understanding nonlinear vibration behaviours in high-power ultrasonic surgical devices [J]. Proceedings of the Royal Society A Mathematical Physical & Engineering Sciences, 2015,471(2176):20140906.

[13] Emmanuel P. Papadakis Ultrasonic instruments and devices: reference for modern instrumentation, techniques, and technology [M]. New York: Academic Press, 1999:752.

[14] Ding W X, Huang W, Wang X D, et al. Quasiperiodic transition to chaos in a plasma [J]. Physical Review Letters, 1993,70(70):170-173.

[15] Romeiras F J, Bondeson A, Ott E, et al. Quasiperiodically forced dynamical systems with strange nonchaotic attractors [J]. Physica D: Nonlinear Phenomena, 1987,26(1/3):277-294.

[16] Alavarez N P, Marco A B A, Buiochi F, et al. Nonlinear iterative model for langevin ultrasonic rransducers [J]. International Congress & Exposition on Noise Control Engineering, 2010(10):1394-1403.

[责任编辑：任德香]

Nonlinear behaviors of the ultrasonic transducers inthe sound speed measurement experiment

YANG Rui-zhi, LI Xi-chen, CAI Hao-jun, YANG Hu-jiang, XIAO Jing-hua

(School of Science, Beijing University of Posts and Telecommunications, Beijing 100876, China)

In the sound speed measurement experiment, by analyzing the spectrum, the amplitude-frequency characteristic curve and the phase diagram, the transition process from linear state into a nonlinear state was studied when the ultrasonic transmitter and receiver were driven by different frequencies. Rich dynamic behaviors of the ultrasonic transducer were observed, such as quasi-periodic state, frequency doubling phenomena, hysteresis and bistable phenomenon.

ultrasonic transducer; nonlinearity; sound speed

2016-05-31；修改日期：2016-08-09

北京邮电大学大学生创新训练项目；国家自然科学基金项目(No.s61377067，No.11375033)

杨睿智(1994-)，男，山东东营人，北京邮电大学理学院2013级本科生.

指导教师：杨胡江(1976-)，男，四川乐山人，北京邮电大学理学院副教授，博士，从事物理实验教学.

O421.1;O415.5

A

1005-4642(2017)04-0006-05

“第9届全国高等学校物理实验教学研讨会”论文