基于生物地理学算法的稀疏平面阵列优化

栾晓明，姚玉征

(哈尔滨工程大学 信息与通信工程学院，黑龙江 哈尔滨 150001)

基于生物地理学算法的稀疏平面阵列优化

栾晓明，姚玉征

(哈尔滨工程大学 信息与通信工程学院，黑龙江 哈尔滨 150001)

天线阵列的相对旁瓣电平和阵元位置为非线性关系。对于非线性关系求最优值问题，用其他优化算法较难求解，而研究采用智能算法求解是一条值得探索的可行路径。提出了一种混合智能算法——改进生物地理学算法，即对生物地理学算法的迁移算子和变异算子进行改进，以提高种群的进化速率，进而优化对称和非对称稀疏平面阵列。仿真结果表明，与以往的算法相比，该算法提高了优化速率，降低阵列的相对旁瓣电平；阵元在阵列孔径内非对称分布比对称分布，所获得的旁瓣电平更低。

生物地理学算法；稀疏阵列；旁瓣电平；平面阵列

0 引言

面阵比线阵提供更多的参数来对阵列进行控制优化，在工程实现中更多的用面阵来对天线信号进行发射(接收)。对于复杂形状的大型平面相控阵天线来说，目标函数的最优化问题或约束条件具有多参数、非线性、不可微或不连续等特点[1-2]。1994年，Haupt采用遗传算法(Genetic Algorithm，GA)优化稀疏阵列，获得比较低的相对旁瓣电平值，且得到稀疏平面阵列的优化结果，一直以来都是该类问题研究的经典参考[3]。黄伟采用FFT算法对平面阵列进行优化，得到比以往文献更低的峰值旁瓣电平；但在优化过程中，不能较好地获得全局最优解，即易于陷入局部最优解[4]。

对不同的基准函数，生物地理学算法(Biogeography Based Optimization，BBO)已被证明了有良好的收敛特性[5]。很多学者对BBO进行了进一步的研究，并与其他的智能算法进行混合，得到了一些性能更好的混合算法[6-14]。Singh等人首次将BBO算法运用于阵列天线的优化综合中，获得良好性能的稀疏阵列天线，但由于BBO算法的编码用的是实数编码，只能对阵列的激励幅度进行优化，在特定方向上形成零陷，达到降低旁瓣电平并提高天线的性能的目的[15-16]。由于只有实数编码，限制了阵元的稀疏。本文对BBO中的迁移算子和变异算子进行改进，得到一种改进的生物地理学算法(Modified Biogeography-Based Optimization，MBBO)，进而优化稀疏平面阵列,并构造相对旁瓣电平的适应度函数，阵元位置作为优化变量，来降低稀疏阵列的旁瓣电平。

1 生物地理学算法概述

生物地理学是研究生物物种自然分布机制的科学，其生物地理学优化算法是由Simon[6]于2008年提出的一种新型全局优化算法，并模拟生物地理学相互独立的栖息地之间生物物种的迁移、变异及其消亡等规律而设计的群智能优化算法。该算法主要通过模拟生物群体在岛屿之间的迁移，实现岛屿之间信息的共享与交流，从而获得问题的最优解。

2 阵列的最优化模型

稀疏平面阵列与稀疏直线阵列相似，即在平面阵列中，从等间距栅格上按照一定比例删除一些数目的阵元来获得稀疏平面阵。假设将T个阵元放置在栅格间距为dx=dy=d,总栅格数为M×N的矩形平面阵内，来获得一个稀疏的平面阵列天线。

假设稀疏面阵的稀布率为：

(1)

若由矩形栅格组成的平面阵列，其主波束指向阵列中心法线的方向，即θ0=90°，则平面阵列的方向图函数可以表示为：

(2)

式中，k=2π/λ，其中λ为波长；方向参数u和v分别表示为u=sinθcosφ，v=sinθsinφ；俯仰角θ和方位角φ的取值范围分别为θ∈[0,π/2]，φ∈[0,2π]；则u和v的取值范围分别为u∈[-1,1]，v∈[-1,1]。Imn为第(m，n)个阵元的激励电流幅度，而且其取值范围为0≤m≤M-1，0≤n≤N-1。如果第(m，n)阵元被稀疏，则Imn=0，否则Imn=1。

与稀疏优化直线阵列相似，在计算PSLL的过程中需要排除阵列的主瓣区域；然后将最优化问题转换为一个组合优化问题来求解，通过列举所有可能存在的阵列结构形式，来在阵列空间中搜寻具有最优PSLL性能的稀疏面阵，以此获得问题的最优解。

3 改进生物地理学算法分析

本文中MBBO算法的进化过程主要有3个步骤：

① 初始化。本文随机的产生N个栖息地的适应度指数变量(Suitability Index Variables， SIV)，一个栖息地供一个种群生存，每个栖息地包含有M个SIV，对应M维变量。所有栖息地的SIV组成的矩阵为X=[X1;X2;…;XN]，其中向量Xi=[xi1,xi2,…,xiM]。

② 改进迁移算子。BBO算法是一种模仿物种在地理上分布与迁移特性的寻优算法，并设计了个体的移动算子，使得不同个体间可以共享信息。每个个体都有一组基于当前物种数目的迁入速率(λ)和迁出速率(μ)，用来控制个体间信息的移动速率。λ和μ关于物种数量p的线性函数为：

新时代基层统战工作创新发展研究——基于以重庆市为重点的调查………………………………………………… 许道权（6·76）

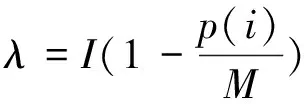
(3)

(4)

式中，M为栖息地容纳生物种类最大数量，p(i)是栖息地i的种群数量。通常考虑最大迁入率和最大迁出率相等的情形，即I=E。

BBO算法的主要算子是迁移算子，其充分利用种群间的信息，提高解的质量，使得算法的开发能力增强。但该算子只是对优良解的SIV和劣质解的SIV进行简单替换，容易引起种群的多样性单一，陷入局部最优解。在算法的进化过程中，优秀个体进化的几率很小，影响算法的收敛速度。因此对迁移算子进行改进，来提高进化效率，获得更好的父代个体。改进的迁移算子其对应方程为：

(5)

式中，Hbest(SIV)为最优解向量；Hi(SIV)，i={1,2,…,M}表示第i个解的向量，M为种群大小；Hq(SIV)、Hk(SIV)为2个互不相同的解向量。rrand为随机数且rrand∈[0,1]；α为实数即α∈[0,1]。

③ 改进的变异算子。自适应变异操作根据每一代群体中个体适应度值的情况动态调整变异概率。当个体适应度值趋于相同时，增大变异概率，以增加种群的多样性；当个体适应度值相差较大时，减小变异概率，以便保存优良个体，加快收敛速度。当栖息地个数为s，并假设栖息地有s种的物种，那么栖息地中具有s种物种数量的概率为Ps。栖息地内物种发生变异现象的概率与其存在的物种数量概率Ps成反比，则每个栖息地的变异算子对应的方程如下：

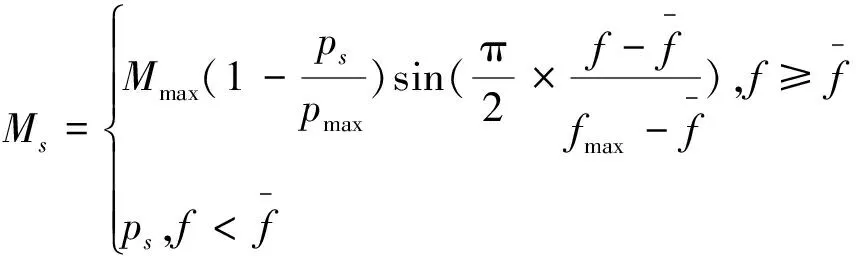
(6)

式中，fmax为每代群体中最大适应度值；f为每代群体平均适应度值；f为参与进行变异个体的适应度值；Mmax为最大变异率；Ps=arg(max(Ps))，s=1,2,…,n。其中Ps的表达式为：

(7)

变异算子根据变异概率的大小来随机挑选变异的栖息地，因此变异概率越大，则栖息地越易发生突变，反之变异概率越小的栖息地越不易发生突变。

4 仿真分析

通常，稀疏优化平面阵列包括2种情况：第一种情况是将孔径分为4个象限，只对第一象限的阵元位置进行稀疏优化，接着将优化后得到的阵元位置通过y轴对称到第二象限，最后将第一二象限的阵元关于x轴映射到第三四象限，得到对称稀疏优化的平面阵列；第二种情况为阵元在阵列孔径内随机优化稀疏的非对称平面阵列。利用智能算法对平面阵列的阵元进行稀疏优化时，首先依据稀布率来确定阵元数目，并随机生成一个稀疏面阵；然后采用智能算法对其进行多次迭代寻优，获得稀疏优化的平面阵列，以保证具有良好的阵列天线性能。

本节主要讨论将MBBO算法应用于优化稀疏平面阵列中，对平面阵列中的阵元位置进行优化，来达到降低旁瓣电平的目的。

4.1 稀疏对称平面阵列

文献[3]通过采用GA来对平面阵列进行稀疏优化综合，将阵元分布在均匀规则的矩形栅格(dx=dy=λ/2)上。在文献[3]中，利用GA对阵元数目为108，即稀布率为54%；孔径为9.5λ×4.5λ的矩形栅格平面阵列进行稀疏优化；在φ=0°平面内PSLL=-20.17 dB，φ=90°平面内PSLL=-19.76 dB的稀疏平面阵列方向图，即文献[3]的图9所示；阵元的位置分布参考文献[3]的图7所示。在相同的初始条件下，将本文的MBBO算法应用于已知阵元数目，即稀布率一定且孔径大小确定的条件下，以阵元优化分布在均匀矩形栅格上来达到稀疏面阵的目的。

为验证MBBO算法的有效性和准确性，设置与文献相同的初设条件，通过仿真试验得到阵列方向图的PSLL=-20.51 dB；其中在φ=0°平面时，PSLL=-20.64 dB；当在φ=90°平面时，PSLL=-21.02 dB。其中，圈为该位置的阵元被删除；黑点表示该位置存在阵元。

分析图1～图3可知，采用MBBO算法对平面阵列进行稀疏优化，旁瓣电平得到降低；与文献[3]相比，本文在φ=0°平面时旁瓣电平比其降低了0.47 dB；而在φ=90°平面时旁瓣电平比其降低了1.26 dB。阵元在阵列孔径内更加地集中在阵列孔径的中心位置，这也说明，平面阵列的方向图与阵列孔径中心布置的阵元数目有直接的关系；进一步验证了在线阵中所提出的观点，即阵列孔径的中心位置固定一定的阵元数目可以进一步降低旁瓣电平，同时减少了优化所需时间。

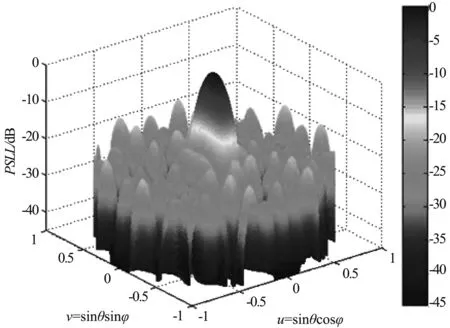
图1 优化后的对称稀疏平面阵列的方向图

图2 对称稀疏面阵方向图的切面图

图3 稀疏后对称面阵阵元分布(白为0，黑为1)

4.2 稀疏非对称平面阵列

文献[4]采用FFT算法对平面阵列的阵元在阵列孔径内非对称分布的稀疏优化综合；将阵元在均匀规则的矩形栅格(dx=dy=λ/2)内，通过FFT随机地优化来布置阵元。从文献[4]的仿真中可知，利用FFT算法对阵元数目为108，即稀布率为54%；孔径为9.5λ×4.5λ的平面阵列进行非对称稀疏优化设计时，可以获得PSLL=-19.69 dB；在φ=0°平面时，PSLL=-20.85 dB；在φ=90°平面时，PSLL=-21.29 dB，参考文献[4]的图4所示的稀疏平面阵列方向图；阵元的位置参考文献[4]中的图4.9(a)所示。

利用MBBO算法在相同的初始条件下，对平面阵列进行非对称稀疏优化，得阵列方向图的PSLL=-19.87 dB；其中，在φ=0°平面时，PSLL=-20.13 dB；当在φ=90°平面时，PSLL=-22.48 dB。其中，圈为该位置的阵元被删除,黑点表示该位置存在阵元。

通过对稀疏非对称平面阵列的仿真来得到阵列方向图及阵元位置分布情况。由图4和图5可得，当对平面阵列进行阵元位置在阵列孔径内非对称稀疏时，旁瓣电平得到一定的降低。与文献[4]中的图4.9(b)相比，本文的MBBO算法优化所得的非对称稀疏平面阵列的旁瓣电平比其降低0.18 dB；但在φ=0°平面上的旁瓣电平有所升高，大约升高0.72 dB；在φ=90°平面内的旁瓣电平值降低了1.19 dB。从图6中可知，阵元也是主要集中于阵列孔径的中心位置。与文献[4]的图4.9(a)相比，孔径中心有几个阵元被稀释，导致在某个方向上的旁瓣电平发生恶化，这也说明，阵列孔径中心的阵元数目对阵列的旁瓣电平有重要的影响。

图4 优化后的非对称稀疏平面阵列的方向图

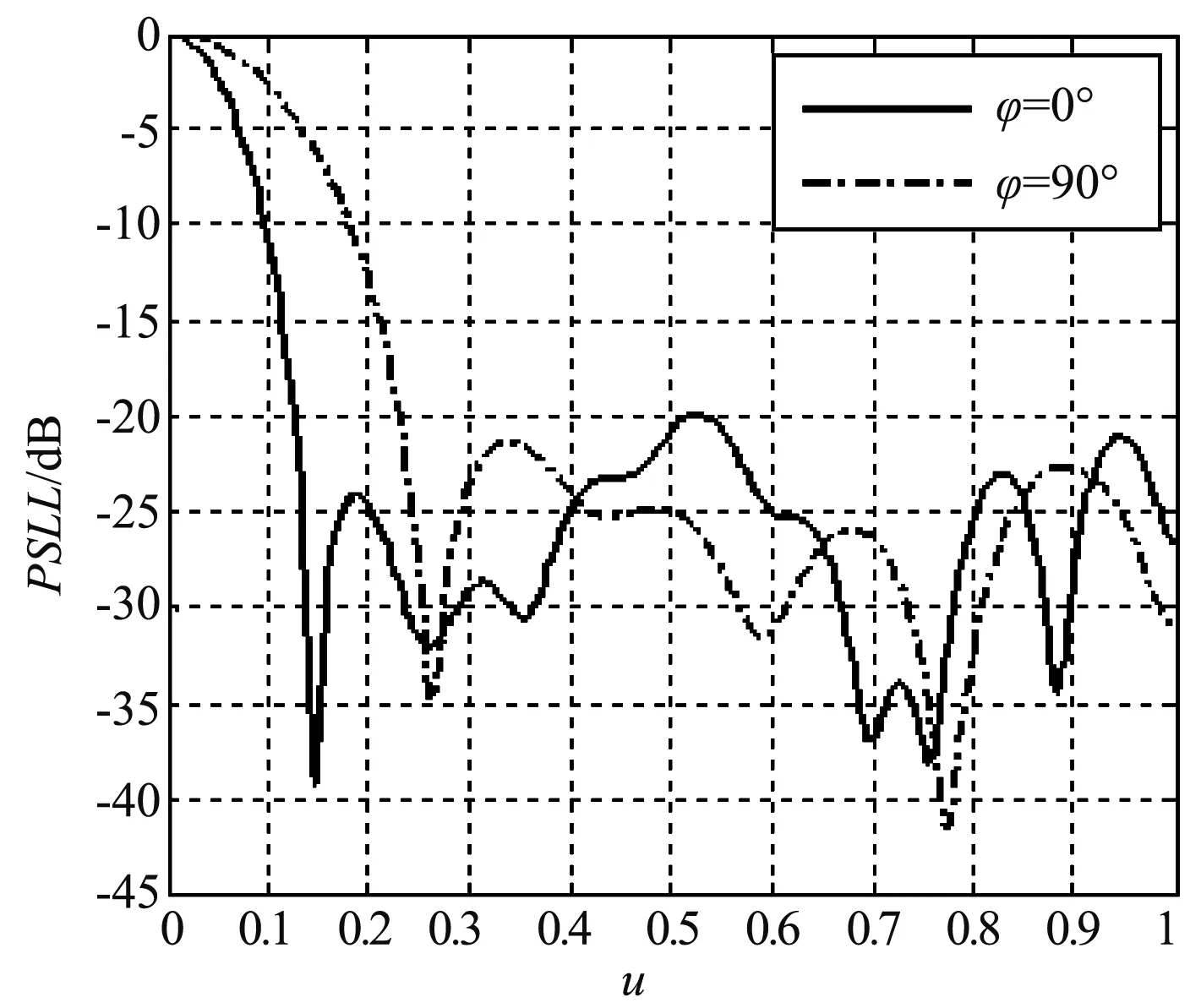
图5 非对称稀疏面阵方向图的切面图

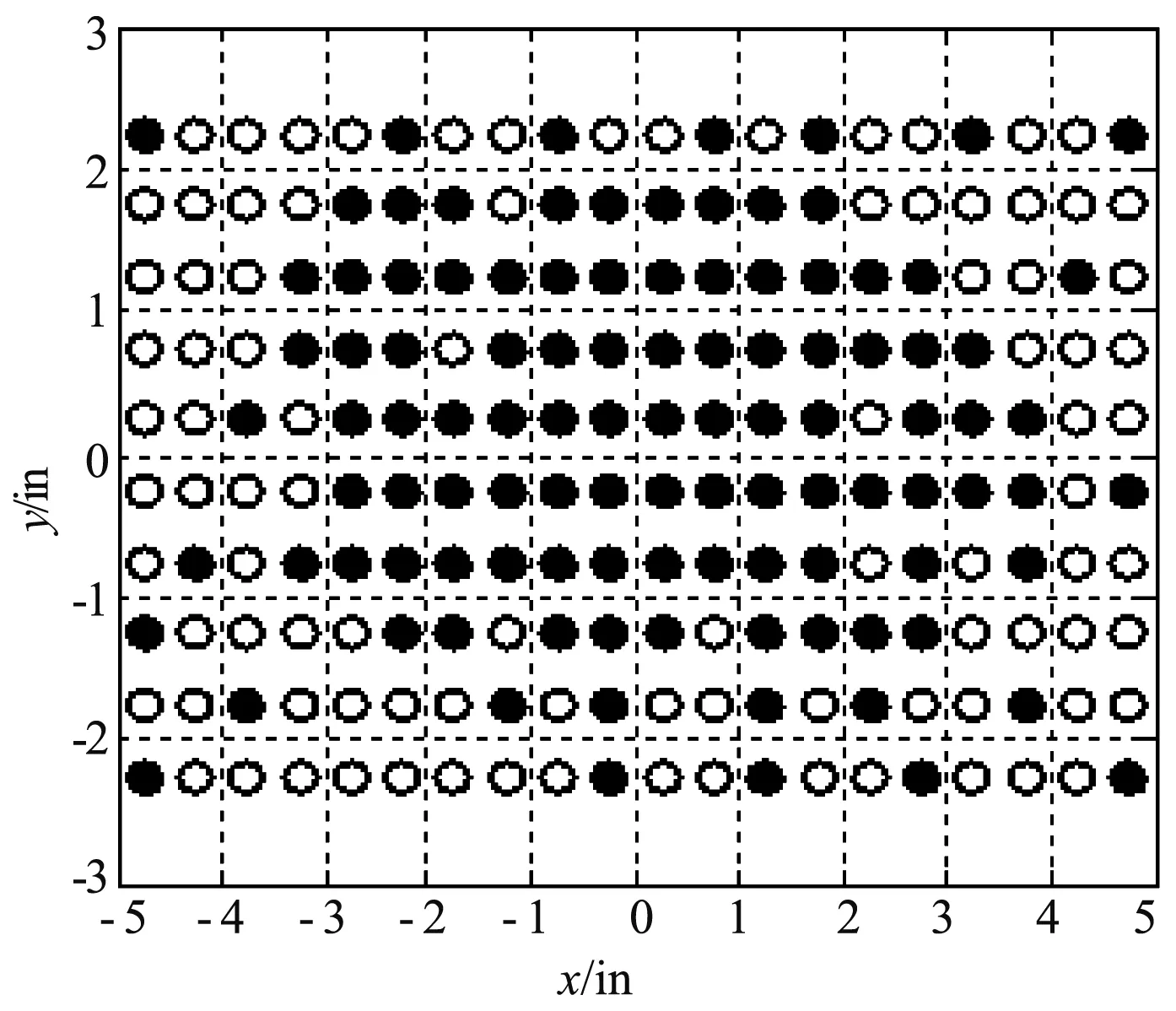
图6 稀疏后非对称面阵阵元分布(白为0，黑为1)

5 结束语

本文对BBO算法进行改进，得到MBBO算法，进而采用该算法优化稀疏平面阵列，并与GA和FFT算法行对比。通过仿真可知，MBBO算法优化稀疏平面阵列所得的旁瓣电平比GA和FFT算法所得旁瓣电平改善了0～2 dB，且非对称阵列比对称阵列具有更低的旁瓣电平。证明了采用MBBO算法优化稀疏平面阵列时，该算法具有良好的有效性和稳定性，阵元在阵列孔径内分布。本文的探讨丰富了MBBO算法在平面阵列综合中的应用，对中小型平面阵列的优化稀疏设计提供了有价值的参考。在优化阵列时，尚未考虑相邻两阵元间的互耦，进一步亟待解决研究的问题是考虑阵元间的互耦问题。

[1] Keizer W P M N.Synthesis of Thinned Planar Circular and Square Arrays Using Density Tapering [J].IEEE Transactions on Antennas and Propagation，2014，62(4)：1555-1563.

[2] Cheng Y F，Shao W，Zhang S J，et al.An Improved Multi-objective Genetic Algorithm for Large Planar Array Thinning [J].IEEE Transactions on Magnetics，2016，52(3):1-1.

[3] Haupt R L.Thinned Arrays Using Genetic Algorithms [J].IEEE Transactions on Antennas and Propagation，1994，42(7)：993-999.

[4] 黄 伟.稀布阵列天线的阵元分布优化设计研究[D].成都：电子科技大学，2012.

[5] Simon D.Biogeography-based Optimization [J].IEEE Transactions on Evolutionary Computation，2008，12(6)：702 -713.

[6] 鲁宇明，王彦超，刘嘉瑞，等.一种改进的生物地理学优化算法[J].计算机工程与应用，2016，52(17)：146-151.

[7] Ma H，Simon D，Fei M.Statistical Mechanics Approximation of Biogeography-based Optimization [J].Evolutionary Computation，2016，24(3)：427-458.

[8] Chai W C，Dong H B，He et al.A Biogeography-based Optimization Algorithm with Multiple Migrations [C]∥15th International Conference on Computer & Information Science，2016：1-8.

[9] Chen X，Lui G H，Du W L，et al.Biogeography-based Optimization with Covariance Matrix Based Migration [J].Applied Soft Computing，2016，45：71-85.

[10]Goudos S K，Siakavara K，Sahalos J N.A Comparative Study of Different Biogeography-based Optimization Migration Models Performance on Antenna Array Thinning Problems [C]∥International Conference on High Performance Computing & Simulation，2016：270-277.

[11]徐以坤，余 洋，米增强，等.基于微分进化的混合生物地理学约束优化算法[J].计算机工程与设计，2015，36(7)：1927-1931,1937.

[12]Cheng G，Lv C，Yan S，et al.A Novel Hybrid Optimization Algorithm Combined with BBO and PSO [C]∥2016 Chinese Control & Decision Conference，2016：1198-1202.

[13]Ren Z W，Zhu Q G.Hybrid Algorithm Based on Biogeography-based Optimization and Differential Evolution for Global Optimization [C]∥9th IEEE Conference on Industrial Electronics & Applications，2014：754-758.

[14]Singh U，Kumar H，Kamal T S.Design of Yagi-Uda Antenna Using Biogeography-based Optimization [J].IEEE Transactions on Antennas and Propagation，2010，58(10)：3375-3379.

[15]Singn U，Kumar H，Kamal T S.Linear Array Synthesis Using Biogeography-based Optimization [J].Progress in Electromagnetics Research M，2010，11：25-36.

[16]Singh U，Kamal T S.Design of Non-uniform Circular Antenna Arrays Using Biogeography-based Optimization [J].IET Microwaves，Antennas and Propagation，2011，5(11)：1365-1370.

Optimization of Thinned Plane Arrays Based on Biogeography-based Optimization Algorithm

LUAN Xiao-ming，YAO Yu-zheng

(College of Information and Communication Engineering，Harbin Engineering University，Harbin Heilongjiang 150001，China)

The relation between the relative side-lobe level of the antenna array and the position of the element is non-linear.It is usually difficult to solve the optimal value problem of nonlinear relation with other optimization algorithms，and it is a feasible way to explore the solution using the intelligent algorithm.In order to improve the rate of population evolution and optimize symmetric and asymmetric thinned planar arrays，a hybrid intelligent algorithm，or Modified Biogeography Based Optimization (MBBO) algorithm is proposed，and the migration and mutation operators are improved in the algorithm.Simulation results show that compared with the previous algorithms，the proposed algorithm improves the optimization rate and reduces the relative side-lobe level of the array.The obtained side-lobe level is lower in the case of asymmetric distribution of the element in the aperture of the array than in the case of symmetry distribution.

Biogeography-Based Optimization (BBO)；thinned arrays；side-lobe level；plane arrays

10.3969/j.issn.1003-3114.2017.03.08

栾晓明，姚玉征.基于生物地理学算法的稀疏平面阵列优化[J].无线电通信技术,2017,43(3)：34-37,67.

[LUANXiaoming，YAOYuzheng.OptimizationofThinnedPlaneArraysBasedonBiogeography-basedOptimizationAlgorithm[J].RadioCommunicationsTechnology，2017,43(3):34-37,67.]

2017-01-19

栾晓明(1963—)，男，教授，主要研究方向：宽带系统的信号检测、处理与识别。姚玉征(1989—),男，硕士研究生，主要研究方向：阵列天线、优化算法。

TN820.1

A

1003-3114(2017)03-34-4