一种基于改进Lloyd-Max的信道估计算法

谷双春，张润生

(1.装备工程技术研究实验室，河北 石家庄 050081；2.中国电子科技集团公司第五十四研究所，河北 石家庄 050081)

一种基于改进Lloyd-Max的信道估计算法

谷双春1，2，张润生1，2

(1.装备工程技术研究实验室，河北 石家庄 050081；2.中国电子科技集团公司第五十四研究所，河北 石家庄 050081)

针对基于Lloyd-Max的平衰落信道估计算法估计精度低且无法适用于高阶QAM调制的问题，提出了基于改进Lloyd-Max的信道估计算法。该算法结合信源的具体调制样式，对Lloyd-Max算法的聚类过程施加星座图结构约束，从而避免了聚类后星座图结构畸形的问题，提高了信道参数估计精度。仿真试验表明，该算法相比于Lloyd-Max算法在较低信噪比下具有更高的信道参数估计精度，在调制阶数较高时，这种优势更加明显。

星座图；信道估计；Lloyd-Max；平衰落

0 引言

当前无线通信是进行信息交换的重要手段之一，其通信质量对日常工作、生活有很大的影响[1]。在无线通信中信道传输特性的未知性是制约无线通信质量提升的主要因素[2]。通过无线信道的估计技术提升无线通信质量是目前无线通信技术中研究的重点问题之一[3-5]。

无线信道分为平衰落信道和选择性衰落信道。城市移动通信信道、对流层散射信道、短波电离层反射信道是典型的选择性衰落信道[6-7]；卫星通信、微波接力通信等通信信道在大多数情况下可以近似为平衰落信道[8-10]。本文仅针对平衰落准静态信道估计问题展开研究。文献[11]针对平衰落准静态信道，提出了基于Lloyd-Max算法的信道衰落系数估计算法，该算法等价于机器学习中的kmeans聚类算法[12]，实现了对平衰落准静态信道的高精度估计；文献[13]针对Lloyd-Max算法运算量较大的问题，提出了基于高阶统计量的平衰落准静态信道的估计算法，该算法借鉴通信侦察[14]中MPSK信号的幅度和相偏的估计技术，实现了MPSK在平衰落准静态信道中的衰落系数的估计，以牺牲一定的估计精度为代价，实现了低运算量的信道估计。文献[15]指出基于Lloyd-Max的信道衰落系数估计算法仅能适用于MPSK等恒包络调制信号，而不适用于诸如QAM等非恒包络调制信号，针对该问题将16QAM分解为4个QPSK，开发了多级Lloyd-Max算法，从而实现了非恒包络调制信号的信道估计[16]。

文献[15-16]中的Lloyd-Max类信道估计算法利用接收信号星座点的聚集特性，通过聚类实现信道估计。深入分析该类算法可知，其没有利用通信信号的特定星座图结构这一先验信息，导致在低信噪比条件下算法难以收敛。针对该问题，本文利用接收信号的星座图结构约束Lloyd-Max算法的聚类过程，提出了基于改进Lloyd-Max的信道估计算法(MLloyd-Max)，实现了平衰落信道的高精度估计，并可适用于高阶QAM调制信号的信道估计。

1 平衰落信道模型

平衰落准静态信道一般为单径模型，用一个复衰落系数描述，其信道模型如式(1)所示[11]：

yk=h·rk+nk,k=1,…,L。

(1)

该模型为码元速率抽样模型，假设系统已经完成载波同步和定时抽样。式中，yk为第k个接收符号，rk为信源发送的第k个符号，nk为第k个码元时刻的噪声，其为零均值加性高斯白噪声(AWGN)，接收符号个数为L，h为平衰落信道的衰落系数。因此平衰落准静态信道的信道估计问题就可转化为信道衰落系数的估计。

2 基于Lloyd-Max的信道估计算法

② 对于接收符号数据集合中的每个数据点yk，取与其距离最近的Cm作为其聚类中心Ck，实现对数据集合Y的聚类；

(1)

(2)

式中，Nm为以Cm作为聚类中心的接收符号的个数，Cn为yn的聚类中心。

通过以上步骤可以将数据聚为M类，当算法收敛后，满足：

可得信道衰落系数h的估计值为：

(3)

3 基于改进的Lloyd-Max算法的信道估计算法

分析第1节基于Lloyd-Max算法的信道估计算法可知，该算法完全通过对接收数据符号的聚类来估计信道衰落系数。其初始聚类中心点集合满足给定调制样式星座图的结构约束，而随着聚类过程不断迭代，各个聚类中心会发生变化，聚类中心构成的结构与标准的星座结构发生畸变，最终影响信道衰落系数的估计精度。这里通过对聚类过程加入星座图结构约束，提出基于改进的Lloyd-Max算法的信道估计算法，以提高衰落系数的估计精度。该算法的步骤如下：

② 定义目标函数J，设定h的初值为h0:

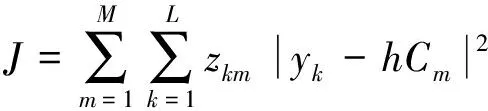
(4)

式中，对于一个给定的衰落系数h，有zkm=1表示第k个接收符号属于第m个聚类中心，即

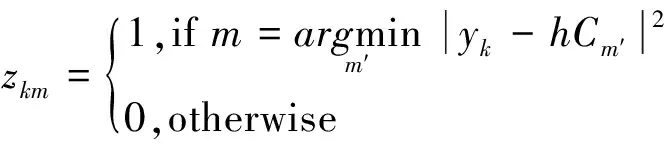
(5)

③ 因此可以通过式(5)确定集合Z：

④ 集合Z确定之后，代入式(4)，通过以衰落系数h为变量对目标函数J取最小化，可得h的估计值为：

(6)

通过以上步骤可得信道衰落系数h的估计值。分析以上过程可以发现，改进的Lloyd-Max算法每次更新聚类中心都是通过衰落系数对初始聚类中心进行缩放，保持了每次聚类中心的星座图结构，从而保证衰落系数的估计精度。

4 非恒包络调制的信道估计问题分析

第2节和第3节中算法过程的阐述都是基于恒包络MPSK信号，本节讨论非恒包络调制信号，如QAM调制的平衰落系数的估计问题。

基于Lloyd-Max聚类算法与机器学习中的kmeans算法等价，而kmeans算法一个很大的不足就是其容易收敛到局部最优点的问题，对于恒包络调制信号，聚类收敛过程简单，这种收敛到局部最优点的问题并不明显。而对于非恒包络调制信号，其收敛到局部最优点的问题尤为突出。在信噪比较低且存在衰落系数的相偏带来星座图旋转的情况下，该问题尤为明显。文献[15]针对该问题提出了基于多级Lloyd-Max聚类算法的非恒包络调制信号的信道估计算法，在一定程度上解决了Lloyd-Max聚类算法收敛到局部最优点的问题。Lloyd-Max聚类算法收敛到局部最优点的问题很多时候都体现为收敛后聚类中心点集形状与标准星座图形状有较大差异，从而造成信道估计精度的降低。本文第3节提出的基于改进的Lloyd-Max的信道估计算法，通过约束每次聚类中心的星座结构，大大降低了算法陷入局部最优点的概率，并且具有适应非恒包络调制信号的能力。由于定量的理论分析较为复杂，对于该问题这里仅给出定性的讨论，对其在信号为非恒包络调制情况下的性能，在第5节的仿真试验部分进行试验性分析。

5 仿真试验

5.1 试验1

本试验仿真分析信源调制方式为QPSK、8PSK时，本文算法的信道估计性能。比对算法为Lloyd-Max算法[11]、HOS算法[13]、本文的MLloyd-Max算法和LS估计下界[13]。试验仿真设置与文献[13]一致。

图1和图2给出了源信号为QPSK和8PSK调制时，平衰落信道衰落系数估计的均方误差(MMSE)随信噪比的变化情况。由图中可见，随着信噪比的升高，3种算法的MMSE都不断减小，且Lloyd-Max算法和本文的MLloyd-Max算法都收敛与LS估计下界。信号调制样式为QPSK时，在信噪比低于5dB时，本文算法的性能明显优于Lloyd-Max算法和HOS算法的估计性能。信号调制样式为8PSK时，在信噪比低于11dB时，本文算法的性能明显优于Lloyd-Max算法和HOS算法。

图1 QPSK平衰落信道估计均方误差

图2 8PSK平衰落信道估计均方误差

5.2 试验2

本试验仿真分析信源调制方式为16QAM时，本文算法的信道估计性能。比对算法为SL-LM算法[15]、ML-LM算法[15]、本文的MLloyd-Max算法和LS估计下界[13]。试验仿真设置与文献[15]一致。

图3给出了不同信噪比下，SL-LM算法、ML-LM算法和本文的MLloyd-Max算法平衰落信道衰落系数估计的均方误差估计(MMSE)。同时给出了LS估计的克拉美罗下界。可以看出3种算法中SL-LM算法性能最差，随着信噪比的增加，该算法的估计性能并不能随之提升。ML-LM算法和本文提出的MLloyd-Max算法的性能都随着信噪比增加而提升。在信噪比低于6dB时，本文MLloyd-Max算法性能要略低于ML-LM算法，而信噪比高于6dB时，本文算法性能优于ML-LM算法，并在信噪比高于16dB时，本文算法的性能收敛于LS下界。信噪比高于16dB时，达到同样MMSE本文算法所需信噪比较ML-LM算法低3dB。

图3 16QAM平衰落信道估计均方误差

6 结束语

现有基于Lloyd-Max的平衰落信道估计算法，使用聚类技术对接收星座图的缩放和旋转，来实现平衰落信道的信道参数估计，但该算法对聚类后的星座点的结构形状没有约束，这样可能会造成星座图收敛为一个畸形的结构，造成信道参数估计的较大误差，并且基于Lloyd-Max的信道估对于阶数高于4的QAM信号，聚类无法收敛到真实的星座图。

针对该问题，结合信源的具体调制样式，对Lloyd-Max算法的聚类过程施加约束，从而避免了聚类后星座图结构畸形的问题，提高了信道参数估计精度。试验结果表明对于QPSK调制，在信噪比低于5dB时，本文算法的性能明显优于Lloyd-Max算法和HOS算法的估计性能；对于8PSK调制，在信噪比低于11dB时，算法的性能明显优于Lloyd-Max算法和HOS算法；对于16QAM调制，在信噪比低于6dB时，算法性能要低于ML-LM算法，而信噪比高于6dB时，优于ML-LM算法，并在信噪比高于16dB时，本文算法的性能收敛于LS下界。

[1]JohnGP，MasoudS.DigitialCommunications(Fifthedition) [M].NewYork：MacGraw-HillCompanies，Inc.，2009.

[2]TongL，XuG，KailathT.BlindChannelIdentificationandEqualizationUsingSecond-orderStatistics：aTime-domainApproach[J].IEEETransactionsonInformationTheory，1994，40(2)：340-349.

[3]CrozierSN，FalconerD.LeastSumofSquaredErrors(LSSE)ChannelEstimation[J].IEEProceedings-F，1991，138(4)：371-378.

[4] 李一杰，周新力，宋斌斌.OFDM系统中基于DFT的信道估计方法[J].无线电工程,2014,44(4):73-76.

[5]LamareRC，SampaionetoR.BlindAdaptiveMIMOReceiversforSpace-timeBlock-codedDS-CDMASystemsinMultipathChannelsUsingtheConstantModulusCriterion[J].IEEETransactionsonCommunications，2010，58(1)：21-27.

[6] 江 漫，王晓亚.一种变步长短波信道盲均衡算法[J].无线电工程,2013,43(2)：38-41.

[7]LiuH，XuG，TongL，etal.RecentDevelopmentsinBlindChannelEqualization：fromCyclostationaritytoSubspaces[J].SignalProcessing，1996，50(1/2)：83-99.

[8]KangW，ChampagneB.Subspace-basedBlindChannelEstimation：GeneralizationandPerformanceAnalysis[J].IEEETransactionsonSignalProcessing，2005,53(3)：1151-1162.

[9] 孙志刚,张 晶.地空测控链路OFDM信道估计[J].无线电工程，2013,43(4)：37-39.

[10]ChatterheeS，FernandoWAC.BlindEstimationofChannelandModulationSchemeinAdaptiveModulationSchemesforOFDM-CDMABased4GSystems[J].IEEETransactionsonConsumerElectronics，2004，50(4):1065-1075.

[11]DizdarO，YilmazAO.BlindChannelEstimationBasedontheLloyd-MaxAlgorithminNarrowbandFadingChannelsandPartial-bandJamming[J].IEEETransactionsonCommunications，2012,60(7):1986-1995.

[12]PerterF.MachineLearning：TheArtandScienceofAlgorithmsthatMakeSenseofData[M].UnitedKingdom：CambridgeUniversityPress，2012.

[13]李啸天，雷 菁， 刘 伟，等.平坦慢衰落信道下基于HOS的PSK调制盲信道估计[J].通信学报，2015，36(5)：140-147.

[14]郑 辉.通信中的盲信号处理理论与技术[M].北京:国防工业出版社,2013.

[15]LiXiaotian，LiJing，LiuWei，etal.BlindChannelEstimationBasedonMultilevelLloyd-MaxIterationforNoncanstantModulusConstellations[J].HindawiJournalofAppliedMathematics，2014(7):1-7.

[16]LloydS.LeastSquaresQuantizationinPCM[J].IEEETransactionsonInformationTheory,1982，28(2)：129-137.

A New Channel Estimation Method Based on Improved Lloyd-Max

GU Shuang-chun1，2，ZHANG Run-sheng1，2

(1.Equipment Engineering Technology Research Laboratory，Shijiazhuang Hebei 050081，China； 2.The 54th Research Institute of CETC，Shijiazhuang Hebei 050081，China)

The existing channel estimation algorithm based on Lloyd-Max has low accuracy and can not deal with high order QAM signal.To solve the problem，the paper proposes an algorithm based on improved Lloyd-Max.Given the modulation pattern，the algorithm imposes a constellation structure constraint on the cluster process of the Lloyd-Max algorithm，which avoids the deformity of the constellation result from the clustering，so it can increase the estimation accuracy of the fading coefficient.The simulation results indicate that the proposed method has higher accuracy than Lloyd-Max under low SNR，which is more evident when the modulation order is high.

constellation；channel estimation；Lloyd-Max；flat fading

10.3969/j.issn.1003-3114.2017.03.14

谷双春，张润生.一种基于改进Lloyd-Max的信道估计算法[J].无线电通信技术,2017,43(3)：56-59.

[GU Shuangchun，ZHANG Runsheng.A New Channel Estimation Method Based on Improved Lloyd-Max [J].Radio Communications Technology，2017,43(3):56-59.]

2017-01-08

谷双春( 1973—)，男，高级工程师，主要研究方向：通信对抗总体技术。张润生 ( 1984—)，男，工程师/博士，通信与信息系统专业，主要研究方向：通信信号处理。

TP391.4

A

1003-3114(2017)03-56-4