基于频响函数虚部奇异值熵的混凝土内部缺陷检测

袁 野，黄晓寒，王仲刚，张 彧

(后勤工程学院 军事土木工程系，重庆 401311)

基于频响函数虚部奇异值熵的混凝土内部缺陷检测

袁 野，黄晓寒，王仲刚，张 彧

(后勤工程学院 军事土木工程系，重庆 401311)

根据相干函数和力锤激励的有效频段来确定频响函数的研究频段，再将频响函数虚部与信息熵理论相结合，计算频响函数虚部构造的Hankel矩阵的奇异值熵，最后通过概率法计算出异常情况的判断值来实现对混凝土内部缺陷的检测。在此基础上提出了一种简单实用的混凝土缺陷成像的定性分析方法，首先利用各扫射射线的奇异谱熵值将试件分为最有可能产生缺陷与最不可能产生缺陷的区域，再计算各缺陷单元格的投影函数值，非缺陷单元格的投影函数值置0，最后用各单元格的投影函数值的等高线来反应混凝土内部情况，并通过试验验证了该方法的有效性。

奇异值熵；频响函数；相干函数；缺陷

工程结构发生损伤时会改变结构的动力特性和动力响应，因此可以根据结构的动力特性和动力响应的改变检测出结构中存在的损伤。其中基于结构的频率、振型等模态参数的改变进行损伤检测的方法得到了广泛的应用，但这些方法属于间接测试方法，其存在由于模态提取误差等因素而降低检测精度的问题，同时存在模态参数受噪声影响较大等问题。为了克服模态参数法的这些缺点，基于振动响应测试的结构损伤检测的频响函数法受到了研究人员的关注[1]。杨彦芳[2]等提出了以频响函数作为损伤识别的基本参量，利用主元分析和多元控制图来识别网架结构损伤的方法。高海洋，郭杏林等[3]仅利用损伤后的板结构频率响应函数虚部，建立二维板结构的损伤定位指标。方剑青，矫桂琼[4]用神经网络BP算法直接对所测结构的频响函数进行分析，用来识别结构的状态。频响函数法在实际应用中具有所使用的传感器及设备较少，测试方便[5], 不需要专门的激振设备[6]等优点；频响函数的虚部更是具有良好的损伤敏感性和抗噪能力[3]。

SHANNON借鉴热力学熵的概念，结合数理统计理论提出了能够用来量化信号的复杂程度的信息熵。当结构出现损伤时，其振动状态的复杂性会发生相应的变化，因此可用反映振动状态复杂程度的熵来评价结构当前的状态[7]。谢中凯等[8]基于近似熵理论，利用自由振动信号对钢筋混凝土梁结构进行了损伤识别。刘国华等[9]基于改进的传递熵理论，对混凝土简支梁进行了损伤识别。

因此笔者提出了一种利用频响函数虚部建立Hankel矩阵，通过计算奇异值熵值来对混凝土内部缺陷进行检测的方法，并在此基础上提出了一种定性分析缺陷的方法。

1 频响函数的理论分析

频响函数不仅包含了信号的幅值、频率和相位的信息，而且还可直接获取，所以频响函数作为判断结构损伤的指标是比较好的。对于单输入单输出的线性系统，其频响函数定义为输出y(t)的傅里叶变换与输入x(t)的傅里叶变换之比，即:

(1)

然而在实际测量中，为消除响应噪声信号的干扰，频响函数通过响应和激励间的自谱实现，表达式为:

(2)

式中：Syy(ω)为响应的功率谱密度;Sxx(ω)为激励的功率谱密度。

2 相干函数频段的选取

图1所示为考虑噪声输入的单输入与单输出系统。

图1 考虑噪声输入的单输入/单输出系统

图1中p(t)与q(t)分别表示真实输入与输出，输入和输出的测量噪声分别为n1(t)和n2(t)，则实际输入和输出的测量值为x(t)=p(t)+n1(t)和y(t)=q(t)+n2(t)。假设噪声n1(t)和n2(t)之间互不相干且噪声与输入输出之间互不相关。

激励与响应的谱相干函数定义为：

(3)

在有噪声的情况下，信号自谱、源信号自谱和噪声自谱的关系为：

(4)

Syy(ω)=Sqq(ω)+Sn2n2(ω)(5)

Sxy(ω)=Spq(ω)(6)

式中：Sxx(ω)为输入端信号自谱;Syy(ω)为输出端信号自谱;Spp(ω)为输入端源信号自谱;Sqq(ω)为输出端源信号自谱;Sn1n1(ω)为输入端噪声信号自谱;Sn2n2(ω)为输出端噪声信号自谱。Sxy(ω)为输入与输出信号自谱;Spq(ω)为输入与输出源信号自谱。

相干函数化为：

(7)

相干函数反映了各频率的信噪比，源信号在某频段的信噪比越大，这个频段的相干函数也越大。因此相干函数在频域上反应了2个信号的相关程度，根据其幅值可以估计出源信号所在的频段[10]。选取信噪比高的频段进行频响函数的分析有利于得到更准确的结果。

图2 力锤敲击产生的脉冲激励及其频谱图

3 激励频段的选取

力锤锤击时，传递给结构的冲击力近乎为半正弦形，如图2(a)所示，其频谱如图2(b)所示。fc为截止频率，fc以下的频段为有效激励频段，fc与脉冲宽度τc有一定的关系[11]：

(8)

综合相干函数与锤击激励得到的各自有效频段，试验采用03 500 Hz频段上的频响函数虚部进行分析。

4 Hankel矩阵奇异谱熵

对测量得到的输入输出数据进行频响分析，提取出上述研究频段内的频响函数虚部的数据，将该数据组成m×n阶的Hankel矩阵：

(9)

式中：m+n-1=N，m≥n。再对H矩阵进行奇异值分解，得到奇异值X0，令s=min(m,n)。奇异值熵定义为：

(10)

pi=δi(∑si=1δi)

(11)

式中：δi为第i个奇异值;pi为第i个奇异值在整个奇异值序列中所占的比重。

当结构发生损伤时，奇异值熵也会发生相应的变化，损伤位置处的奇异值熵较无损伤位置处的奇异值熵大，因而可以用其来表征结构的状态和损伤情况[7]。

5 概率法

对于波速的判断，南京水利科学研究院的罗骐先提出了概率法，概率法认为随机误差引起的混凝土的质量波动是符合正态分布的[12]。将波速按大小顺序进行排列x1≥x2≥…≥xs，然后对数据进行筛选，将位于后面明显较小的数据视为可疑数据，再将这些可疑数据中最大的一个与排在其前面的数据组成一组新数据，对该组数据求其平均值mx和标准差Sx，并按下式求出异常情况的判断值xn>X0：

(12)

式中：λ为根据规范JGJ106-2003《建筑桩基检测技术规范》查得的系数。

得到异常数据判断临界值后，将该值与可疑数据的最大值xn进行比较，若xnX0，则表示xn是正常值，则需对前n+1个数据进行上述的计算和判断。基于此方法，笔者对计算得到的奇异谱熵数据进行类似的处理，根据找到的异常值来判断混凝土内部的缺陷。

6 定性分析方法

在桩基检测中，可以利用声阴影重叠法在初定缺陷区域内仔细判定缺陷的确切位置、范围和性质[13]。类似于声阴影重叠法，在2个方向进行检测，利用奇异谱熵值分别划出阴影区，则2个阴影区内边界线交叉重叠所围成的区域，即为缺陷的范围。为了量化阴影区，首先将试件截面离散成若干网格化单元，然后将射线所经过的单元都赋予该条射线计算得到的奇异谱熵值，最后将网格中的奇异谱熵值进行叠加即为该单元格的投影函数值。

以一个二维模型示意图(见图3)来说明，模型中央设一正方形缺陷，在2个方向进行检测，通过奇异谱熵值初判得到2个阴影区。对于经过缺陷区域的某单元格，奇异谱熵值较大，阴影重叠越多，则穿越其途经缺陷区域的射线越多，进而该单元投影函数值越大。由图可知，则奇异谱熵值：A>B>C，由此判断单元格A最有可能处于缺陷区，这与实际情况相符。

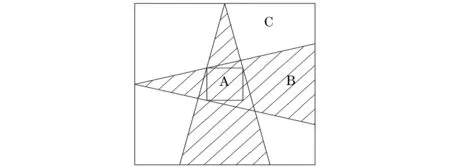
图3 缺陷定性分析的二维模型示意

7 方形混凝土柱缺陷检测

图4 试件图片

设计并制作了规格(长X宽X高)为800 mm×800 mm×150 mm的素混凝土柱试件，该缺陷试件内部缺陷尺寸(长X宽X高)为160 mm×160 mm×150 mm，如图4所示。试验的仪器设备为DH5960超高速动态信号采集仪、KDL力锤和带磁座的加速度传感器。

7.1 模型Ⅰ

采用一发一收对测方式采集信号(均采用同一传感器接收信号)，设置8对测点，其中第4、5测试点是经过缺陷的情况，在每一测点敲击6次，测点布置如图5所示，试验模型Ⅰ如图6所示。

利用测得的输入与输出数据进行频响函数虚部奇异值熵的计算，计算结果如表1所示。

表1中数据按概率法进行计算与判断，最终计算出来的临界值X0=3.930 4。将其与表中数据进行对比发现，在4-4中只有一组数据小于临界值，5-5中的所有数据均大于临界值，故判断4-4与5-5测试条件下为经过缺陷的情况，与实际结果相吻合。

图5 模型Ⅰ测点布置

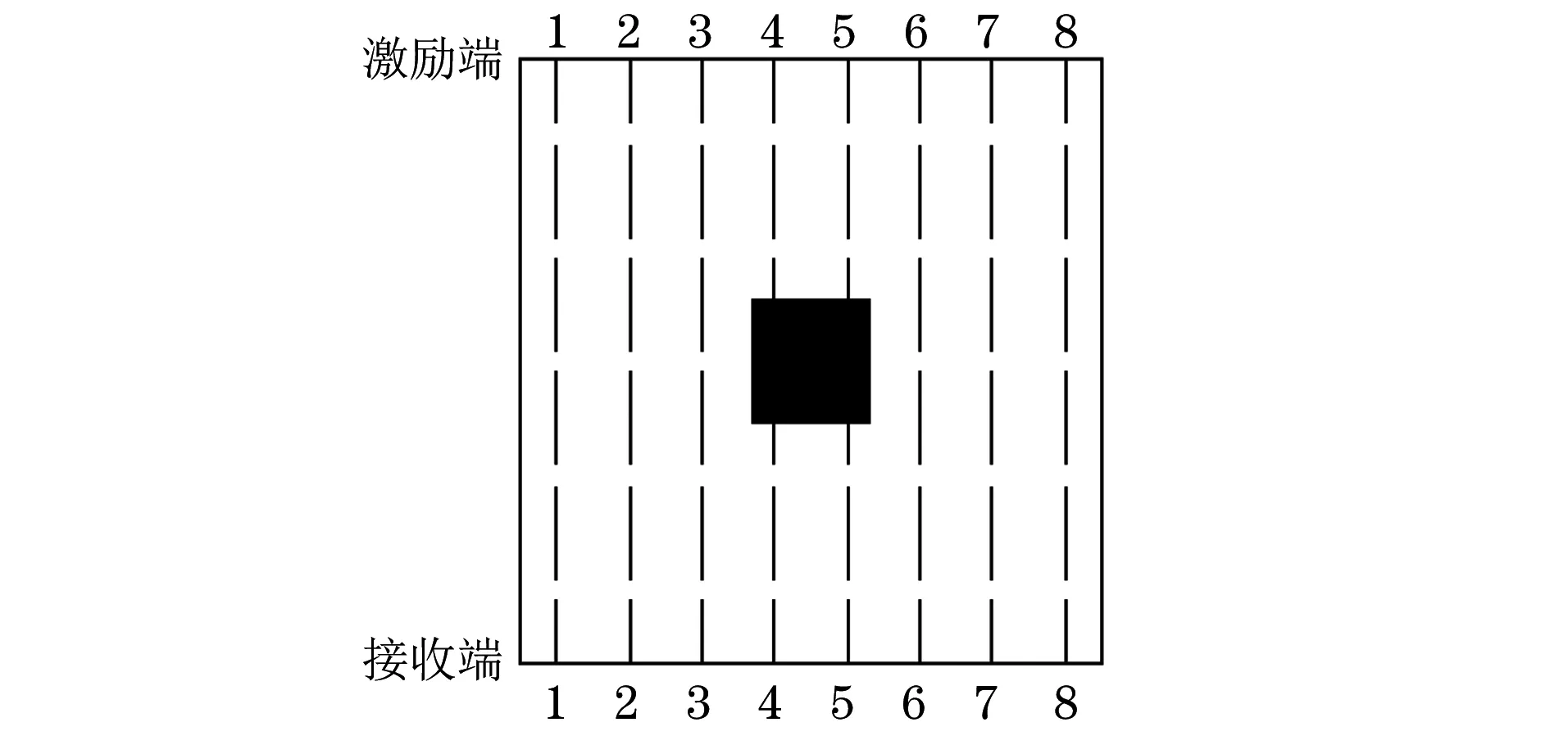
图6 试验模型Ⅰ示意

7.2 模型Ⅱ

采用一发多收方式采集信号，设置8个采集点，在激发点敲击6次，测点布置如图7所示，试验模型Ⅱ如图8所示。

图7 模型Ⅱ测点布置

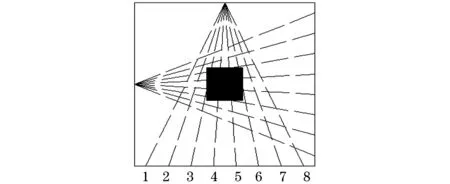
图8 试验模型Ⅱ示意

利用测得的输入与输出数据进行频响函数虚部奇异值熵的计算，结果见表2(限于篇幅，表中只给出其中一侧的计算结果)。

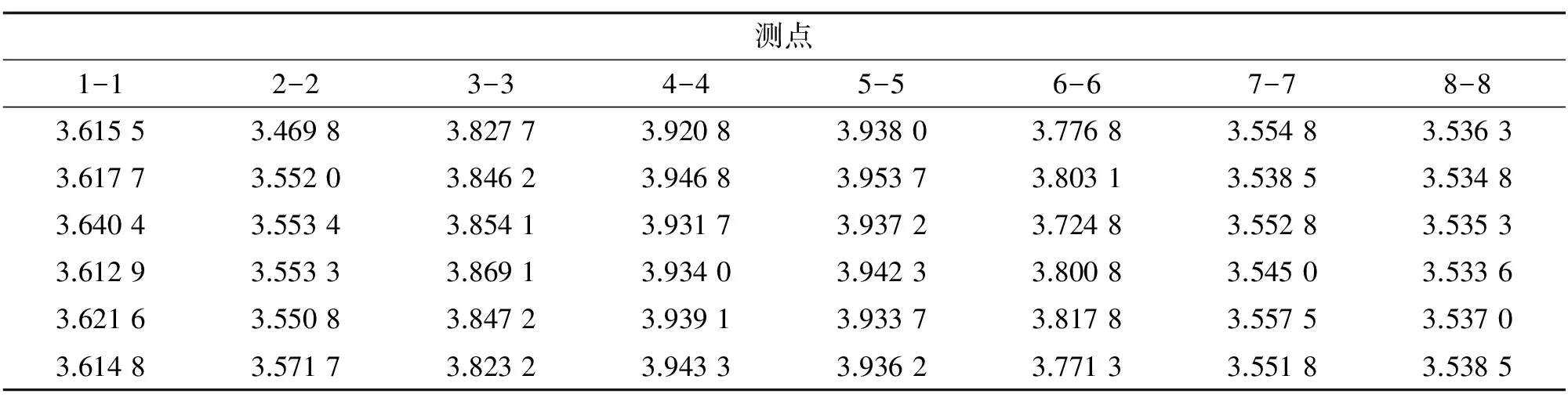
表1 模型Ⅰ试验的奇异值熵计算结果

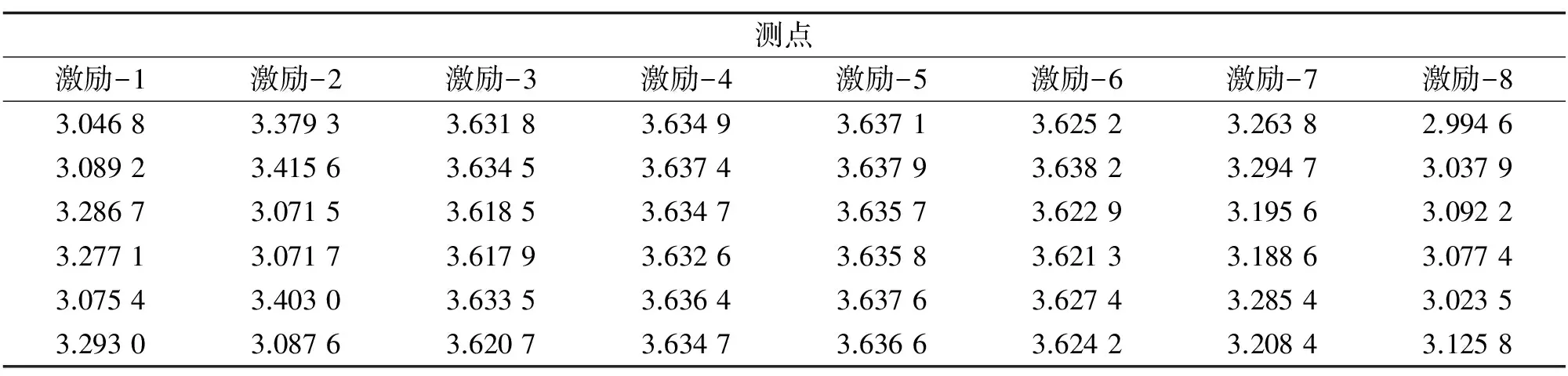
表2 模型Ⅱ试验的奇异值熵计算结果

对表2中数据按概率法进行计算与判断，最终计算出来的临界值X0=3.546 2。将其与表中数据进行对比发现，可以初判激励-3与激励-6围成的阴影区为可疑缺陷区域，再通过另一个方向的测试，得到阴影重叠区即为最有可能产生缺陷的区域，计算重叠区域中网格的叠加投影函数值(奇异谱熵值)，其余网格中的投影函数值置0，做等高线图，如图9所示。

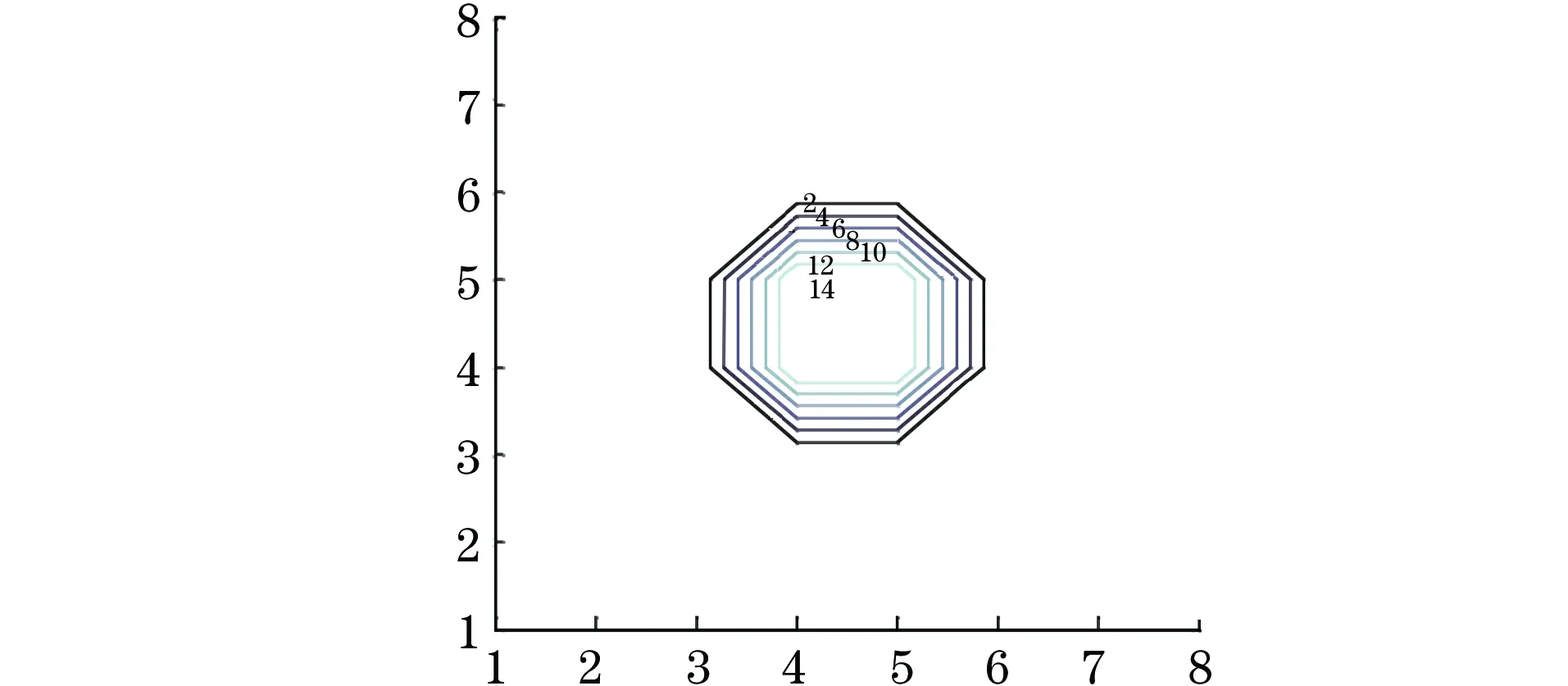
图9 试验模型Ⅱ的奇异值熵等高线图

通过上述步骤，可以重建试件的截面图像，笔者提出的定性分析方法能正确地反映出缺陷的位置，同时也能大致反映出缺陷的区域范围，将定性分析方法与定量反演计算相结合，可以减少误判，提高缺陷识别的准确性和可靠性。

8 结论

通过构建合适频段上的频响函数虚部Hankel矩阵，并对该矩阵进行奇异值分解，计算奇异值熵，最后用概率法对缺陷进行判别。通过奇异谱熵值的计算，再结合提出的定性分析方法，能够对缺陷的位置和范围进行比较准确的估计，可以作为定量反演的辅助判别。所提方法简单直观、产生的误差较小、辨识度较高，而且适用于低信噪比的情况;同时也不需要结构损伤前的数据作为参考，更利于实际工程的应用。

[1] CARDEN E P, FANNING P. Vibration based condition monitoring:a review[J].Structural Monitoring,2004,3(4):355-377.

[2] 杨彦芳，宋玉普. 基于主元分析和频响函数的网架结构损伤识别方法[J]. 工程力学，2007，24(9):105-110.

[3] 高海洋，郭杏林，吴明勇.基于频响函数虚部的板结构损伤检测方法研究[J].振动与冲击，2012,31(12):86-91.

[4] 方剑青,矫桂琼. 基于频响函数的结构状态识别神经网络方法[J]. 振动、测试与诊断, 2007,27(1):45-47.

[5] WANG Z,LIN R M,LIM M K. Structural damage detection using measured FRF data[J]. Computer Methods in Applied Mechanics and Engineering,1997,147:187-197.

[6] YAM L H,LEUNG T P,LI D B, et al. Use of ambient response measurements to determine dynamic characteristics of slender structures[J]. Engineering Structures,1996,18(3):145-150.

[7] 李睿,于德介,曾威. 一种基于奇异谱熵和脉冲响应的结构损伤诊断方法[J]. 振动工程学报,2006,19(3):331-335.

[8] 谢中凯,刘国华. 近似熵在混凝土结构损伤识别中的应用[J]. 浙江大学学报(工学版),2013,47(3):456-463.

[9] 刘国华,谢中凯. 一种用于检测梁结构损伤的改进传递熵[J]. 振动工程学报,2014,27(1):136-144.

[10] 钱济国. 频响函数测量的脉冲激励法[J]. 振动、测试与诊断,1994,14(2):32-39.

[11] 吴佳晔. 土木工程检测与测试[M]. 北京:高等教育出版社,2015.

[12] 罗骐先.桩基工程检测手册[M].北京:人民交通出版社，2003:181-258.

[13] 吴慧敏.结构混凝土现场检测新技术——混凝土非破损检测[M].长沙：湖南大学出版社，1998:161-164.

The Detection of Internal Defects of Concrete Based on the Imaginary Part of the Frequency Response Function and Singular Value Entropy

YUAN Ye, HUANG Xiao-han, WANG Zhong-gang, ZHANG Yu

(Department of Civil Engineering, Logistic Engineering University, Chongqing 401311, China)

Based on the coherence function and effective frequency band of hammer excitation,the frequency band of the frequency response function was determined. Then the imaginary part of frequency-response function and the information entropy theory were combined to calculate the singular value entropy of Hankel-matrix which was constructured by the imaginary part of the frequency-response function. Finally， probabilistic method was used to calculate the abnormal condition and examine the internal defects of concrete. Based on these, the paper offers a simple and practical method of qualitative analysis to image the concrete defect. Firstly, the specimen was divided into two zones to differ in degree of defect.Then the projection function value of the defect cell was calculated and the non-defect cell was set to zero.Lastly, the inside situation of concrete was reacted by the contour of the projection function,and the test was performed to assess availability of the method.

Singular value entropy; Frequency response function; Coherence function; Defect

2016-09-10

袁 野(1992-),男，硕士研究生，主要从事军事特种结构检测及加固。

袁 野, E-mail: 39523046@qq.com。

10.11973/wsjc201704004

TG115.28

A

1000-6656(2017)04-0017-05