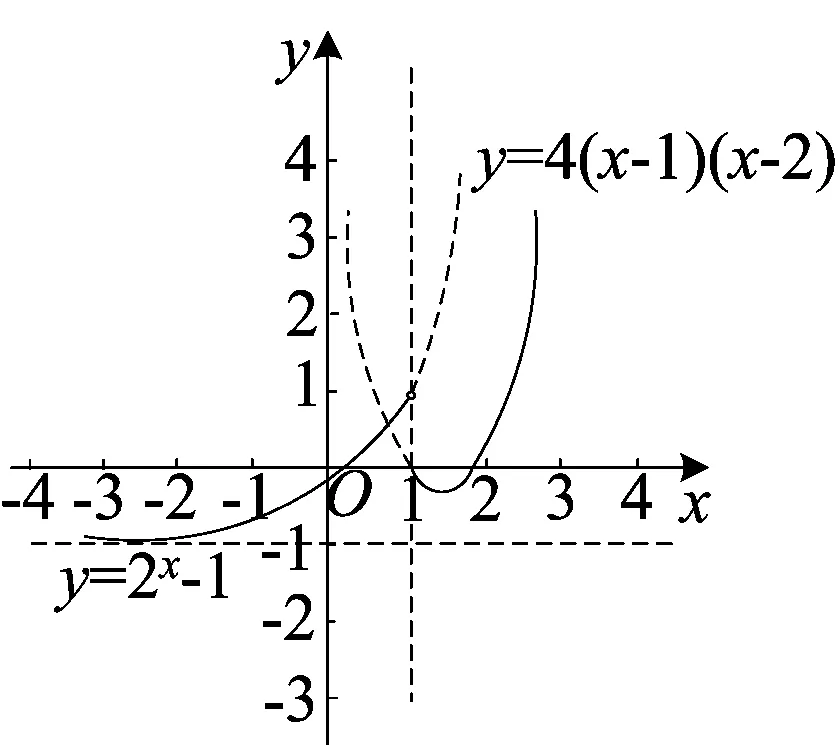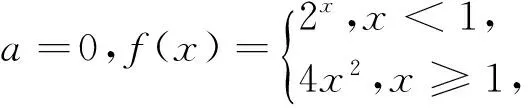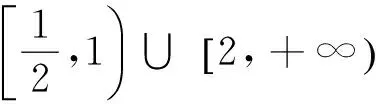含参变量的分段函数的零点问题的特值分析法
罗志强 (邮编:246000)
安徽省安庆市第一中学
含参变量的分段函数的零点问题的特值分析法
罗志强 (邮编:246000)
安徽省安庆市第一中学
近几年高考数学试题出现带参变量的分段函数的零点问题,题型新颖,思维灵活,中等难度,内容丰富,切入点多.本文就图象解法,通过例题来介绍自己的一点探索,期望对大家有所启发.
例1 (2015湖南理)已知
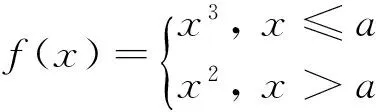
分析 本题函数f(x)的图象是由函数y=x3和y=x2两个函数组合而成的,直线x=a把这两个函数图象分成两个部分,函数f(x)在直线x=a的左半部分是y=x3,右半部分是y=x2.由于a是变化的,故函数f(x)的图象也不断发生变化,为了方便分析,对a取特殊值进行讨论.
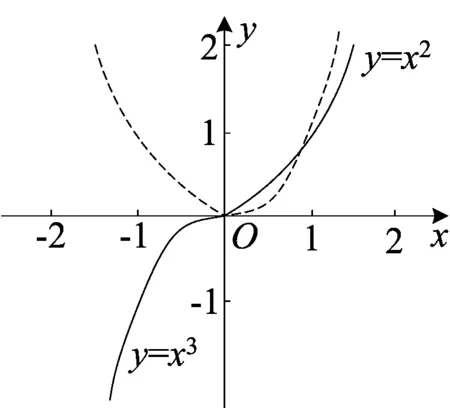
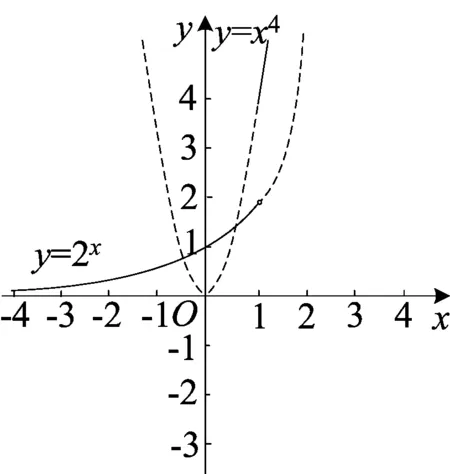
图1

图2
(1)取a=0,如图1.函数f(x)在(-∞,+∞)上是增函数,由题意,是否存在实数b,使方程f(x)=b有两个不等的实数解,故当a=0时不符合题意.又函数f(x)右半部分是y=x2,函数y=x2的图象是抛物线,对称轴是x=0,结合图1知,当a<0时,符合题意.
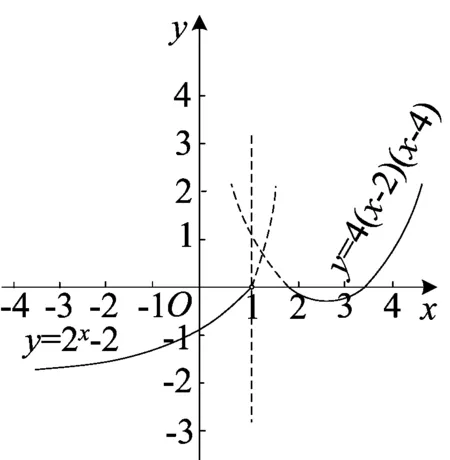
(2)取a=1,如图2. 函数f(x)在(-∞,+∞)上是增函数,从而g(x)也是(-∞,+∞)内的增函数不符合题意.又当a∈(0,1)时,有a2>a3成立,由图象2可知,当a∈(0,1)时,函数f(x)在(-∞,+∞)上是增函数,符合题意.又当a∈(1.+∞)时,有a2 分析 本题函数f(x)的图象是由函数y=2x-a和y=4(x-a)(x-2a)两个函数组合而成的,分段函数的变量取值范围不变,解析式中含有参变量.其中函数y=2x-a的图形是指数函数图形的上下平移,函数y=4(x-a)(x-2a)的零点是a和2a,符合题意的是f(x)恰有两个零点,对a进行讨论.问题是函数y=2x-a是否有零点,且函数y=4(x-a)(x-2a)的零点是否在分段的范围内(x≥1).问题看起来很复杂,若取特殊值来研究就简单了. 图3 图4 图5 结合图3知,当a<0时函数y=2x-a的图象是指数函数图象的向上平移,图象与x轴无交点,且函数y=4(x-a)(x-2a)的零点不是在分段(x≥1)的范围内,故f(x)无零点.所以a≤0不符合题意. (2)取a=1,f(x)= (3)取a=2, 当1 两道试题各有特点,例1分段函数中的变量的取值范围含有参变量,函数解析式中不含参变量,例2则相反,分段函数的取值范围确定,函数解析式中含有参变量.两个函数的图象随参变量取值的变化,函数的图象也在变,千姿百态,丰富多彩,给大家留有变幻想象的空间.虽然图象不确定,但变化有规律.如何思考?怎么切入?我认为图形图象是抓手,从特殊值或极端情况切入,思路简单,机智应变.这两道题有多种解法,都没有图象法简洁明朗,直奔主题.这两道高考试题起点低,落点高,考查常规常法与基础知识基本技能,数形结合,考点多,入口宽.符合高考命题多考想、少考算的命题思维,是难得的函数图象创新题. 2017-01-10)