用GeoGebra探究一类“果圆”问题的轨迹

张新全 邓珍珍 代超群 (邮编：230601)

合肥师范学院数学与统计学院

教 学参 考

用GeoGebra探究一类“果圆”问题的轨迹

张新全 邓珍珍 代超群 (邮编：230601)

合肥师范学院数学与统计学院

将一个绳套套在两个定点上，拉紧并旋转一周可得到一个椭圆，若将绳套套在多个定点上拉紧并旋转，得到的轨迹是什么，有何规律？利用GeoGebra研究发现：当三个定点组成一个边长为2c的等边三角形时，周长为2a+2c的绳套绕成的图形由六段椭圆弧组成，其中三个椭圆弧的长轴为2a，三个椭圆弧的长轴为2a-2c，当绳套绕n个定点旋转时，绕成的图形由2n段椭圆弧组成，进一步得出若干结论.当某个定点变化时，轨迹也发生变化.当绳套的长度变化时，轨迹也发生变化.

椭圆；GeoGebra；“果圆”；轨迹

1 研究背景

在小学和初中学习圆时，老师演示圆的轨迹形成过程，往往把一条线的一端固定在黑板上，另一端系在粉笔上，拉紧线后，粉笔在黑板上旋转一周，即可画出一个圆.在高中学习椭圆时，老师在演示椭圆形成过程时，也往往把一条线的两端固定在黑板上，用粉笔把线拉紧，在黑板上旋转一周，即可画出一个椭圆.现在，我们可以用GeoGebra软件，十分方便地在电脑上演示上述圆与椭圆的形成过程.受此启发，我们把一条线换成一个封闭的线即绳套，然后套在一个固定点上，环绕旋转一周就画出一个圆，而把此封闭的曲线套在两个固定点上，环绕旋转一周就可画出一个椭圆.进一步，如果用一根绳套绕三个固定点旋转会得出什么结果，绕四个定点旋转又会得到什么结果?一直到n个定点呢？借助GeoGebra软件，我们可以画出各种情况下的轨迹，当n≥3时，轨迹不再是椭圆，而是一些椭圆弧组成的封闭曲线，这种曲线我们称之为“果圆” .约定：绳套是指柔软而无弹性的封闭细线.

2 研究思路和内容

2.1 研究思路

由于一个定点和两个定点的情况比较简单，这里我们主要研究三个或三个以上定点的情形.先研究三个定点构成一个等边三角形的情形，将绳套套在等边三角形上，环绕一周得出的轨迹及方程，然后借助GeoGebra，改变三角形的形状，研究轨迹的变化规律.最后再将三角形拓展成凸四边形，凸五边形，凸n边形的情形，再观察轨迹的变化，得出结论.研究方法主要采用实验法和论证法，其中实验法是用GeoGebra软件绘制各种情况下的轨迹.

2.2 研究过程

(1)三个定点构成正三角形

设等边三角形ABC的边长为2c，绳套的周长为2a+2c，其中a>2c>0，将绳套旋转后得到的轨迹分别为椭圆弧A1A2、A2C1、C1C2、C2B1、B1B2、B2A1，利用GeoGebra软件画出各段椭圆弧，如图1.

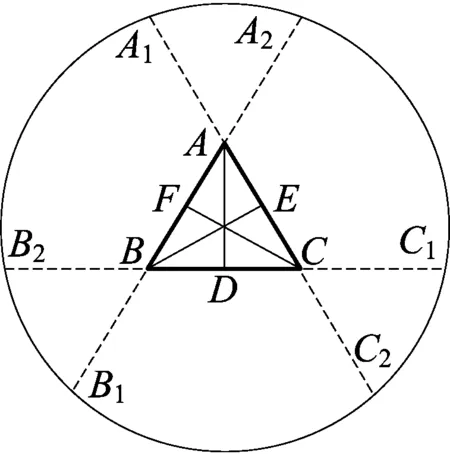
图1

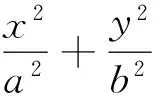
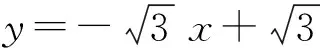
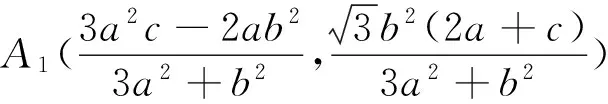
同理，点A2为

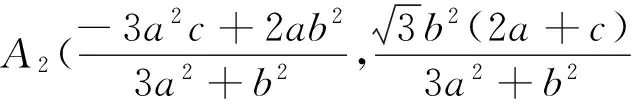
椭圆弧A1A2的方程为

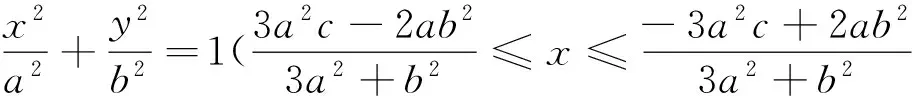
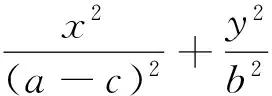
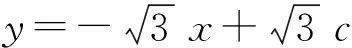
同理可得，点B1为

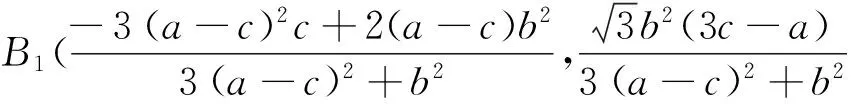
故椭圆弧B1C2的方程为

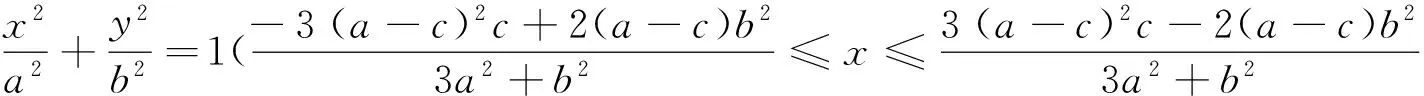
先将坐标原点D平移至正△ABC的中心O，再以O为中心逆时针旋转120°，经过这两次坐标变换，即可由椭圆弧A1A2的方程得到椭圆弧B1B2的方程，在此基础上，再以O为中心逆时针旋转120°，即可由椭圆弧B1B2的方程得到椭圆弧C1C2的方程.(在此不再逐一推导)

将坐标原点D平移至正△ABC的中心O，再以O为中心逆时针旋转120°，经过这两次坐标变换，即可由椭圆弧B1C2的方程得到椭圆弧A2C1的方程，在此基础上，再以O为中心逆时针旋转120°，即可由椭圆弧B1B2的方程得到椭圆弧A1B2的方程.(在此不再逐一推导)

(2)当正△ABC中顶点A沿BC边上的高AD方向运动时“果圆”的变化情况

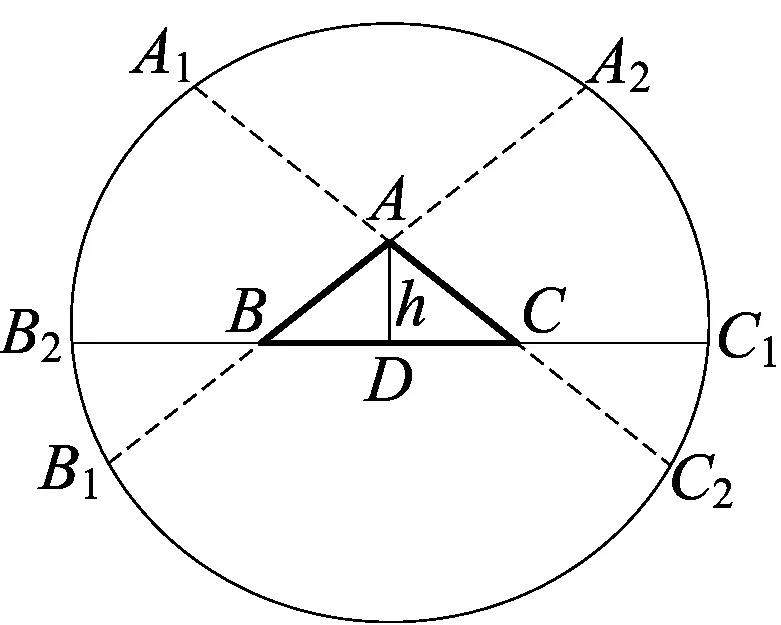
图2

如图2，设AD的长度为h，当h变化时，我们研究这六段弧的变化情况.

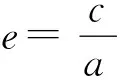
椭圆弧B1C2的长轴为：

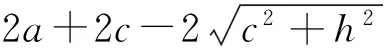
椭圆弧B1B2的长轴为

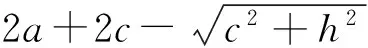
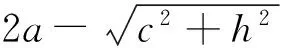
椭圆弧C1C2的长轴为

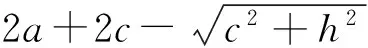
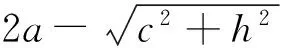
综上所述，当A点沿AD方向向下运动时，椭圆弧B1B2、A2C1、C1C2、A1B2的长轴均增大，离心率均减小，椭圆弧均变圆，弧长均变短，椭圆弧A1A2的长轴、焦距、离心率均不变，弧长变长，椭圆弧B1C2的长轴变长、焦距不变，离心率变小，而弧长变长，当A点移动到D点与B点C点在同一直线上时，椭圆弧B1B2、A2C1、C1C2、A1B2的弧长均变为0，A1A2弧与B1C2弧连成一个完整的椭圆.

(3)三个定点构成任意三角形

当三个定点构成任意三角形时，将绳套套在三角形上，环绕一周得出的轨迹仍是由六段椭圆弧构成的封闭曲线即“果圆”，利用GeoGebra画出轨迹如图3.

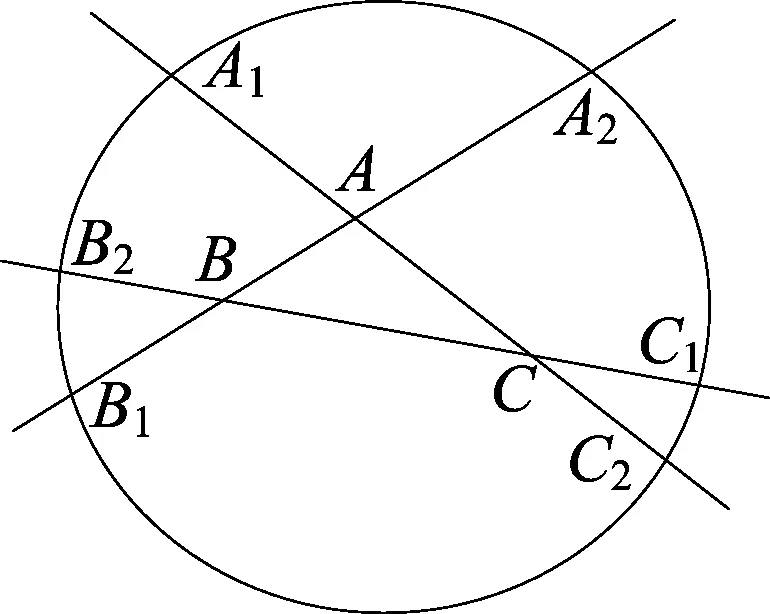
图3

设△ABC的三边长分别为BC=a,CA=b,AB=c,周长p=a+b+c,绳套的长为l,且l>p.

椭圆弧A1A2是以B、C为焦点，以l-a为长轴且夹在射线AA1与射线AA2之间的那段椭圆弧.

椭圆弧B1C2是以B、C为焦点，以l-b-c为长轴且夹在射线AB1与射线AC2之间的那段椭圆弧.

椭圆弧B1B2是以A、C为焦点，以l-b为长轴且夹在射线BB1与射线BB2之间的那段椭圆弧.

椭圆弧A2C1是以A、C为焦点，以l-a-c为长轴且夹在射线BA2与射线BC1之间的那段椭圆弧.

椭圆弧C1C2是以A、B为焦点，以l-c为长轴且夹在射线CC1与射线CC2之间的那段椭圆弧.

椭圆弧A1B2是以A、B为焦点，以l-a-b为长轴且夹在射线CA1与射线CB2之间的那段椭圆弧.

理论上，即便对于不共线的任意三点，如图2的情形，我们仍然能够建立上述六段椭圆弧的方程，但是由于参数过多，建立起来的方程极其复杂，形式也不美观，应用价值不大，我们在此就不再给出它们的方程.用GeoGebra直接作出它们的轨迹，同样是描述轨迹的一种重要方式，且直观生动，易于推广.

利用GeoGebra的动画和动态的功能，当A、B、C三点在平面上随机移动时，就会发现“果圆”的形状也在相应改变；当A、B、C三点不动、让绳套的长度连续变化时，也会发现“果圆”的形状同样在相应改变；当A、B、C三点在平面上随机移动、绳套的长度连续变化时，就会发现“果圆”的形状也在相应改变.

通过GeoGebra的动态演示，我们也会发现：当三点共线时，“果圆”变成一个完整的椭圆.

(4)四个点构成凸四边形

如图4，如果四点A、B、C、D构成凹四边形时，绳套始终不能套到点D，这样问题就转化为已经解决的用绳套套三角形的问题，所以我们只研究四点构成凸四边形的情形.对于其他多边形也是如此，凹进去的点总是套不到，所以我们只要研究凸多边形即可.

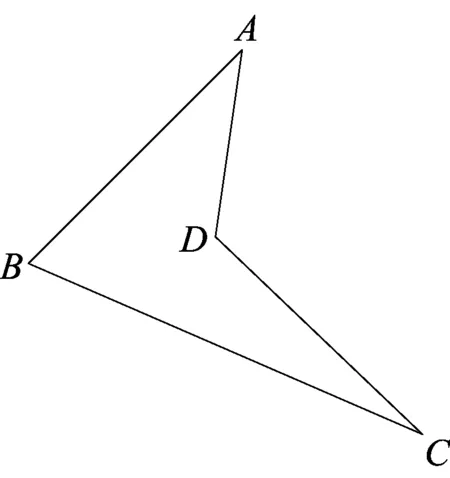
图4

对于任意四边形的情形，问题变得更为复杂，经反复实验，我们发现其复杂性在于：对于有些四边形，只能套住3个点或4个点两种情形，而对于另外一些四边形，却能套住2个点、3个点或4个点三种情形.要想建立所套出轨迹的一般方程，几乎是不可能的.但是用GeoGebra却能十分方便地探究其轨迹，并且能够作出任意给定四边形所能套出的动态轨迹.

下面图5就是用给定长度绳套来套四边形ABCD所得到的“果圆”，它是由8段椭圆弧组成.当改变绳套的长度或四边形的形状时，“果圆”的形状也在相应地变动，请演示GeoGebra文件，感受这种动态变化过程.

注意 由于图形中隐藏的点、线太多，在GeoGebra文件中调整绳套线长度或四边形的形状时务必微调.

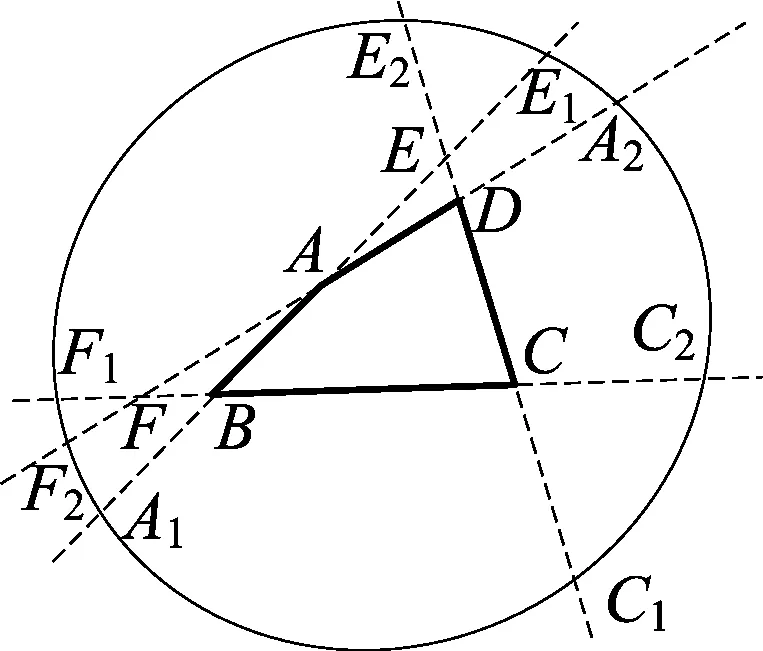
图5

设四边形ABCD的四边长分别记为AB=a,BC=b,CD=c,DA=d. 其周长记为p=a+b+c+d,绳套的周长为l(l>p).下面对图5中的8段椭圆弧予以说明.

同时约定：l>a+b+c+AE+DE且l>b+c+d+AF+BF,否则椭圆弧E1E2与F1F2就会落在有限区域△ADE和△ABF内.

椭圆弧E1E2是以B、C为焦点，以l-b为长轴且夹在射线EE1与射线EE2之间的那段椭圆弧.

椭圆弧E2F1是以B、D为焦点，以l-b-c为长轴且夹在射线FF1与射线EE2之间的那段椭圆弧.

椭圆弧F1F2是以C、D为焦点，以l-c为长轴且夹在射线FF1与射线FF2之间的那段椭圆弧.

椭圆弧F2A1是以A、C为焦点，以l-c-d为长轴且夹在射线FF2与射线BA1之间的那段椭圆弧.

椭圆弧A1C1是以B、C为焦点，以l-c-d-a为长轴且夹在射线BA1与射线CC1之间的那段椭圆弧.

椭圆弧C1C2是以A、D为焦点，以l-a-d为长轴且夹在射线CC1与射线CC2之间的那段椭圆弧.

椭圆弧C2A2是以C、D为焦点，以l-a-b-d为长轴且夹在射线CC2与射线DA2之间的那段椭圆弧.

椭圆弧A2E1是以A、C为焦点，以l-a-b为长轴且夹在射线EE1与射线DA2之间的那段椭圆弧.

(5)n个点构成凸n边形

利用几何画板进行深入探究，我们得出以下一般结论：

在凸n边形A1A2…An中，记A1A2=a1,A2A3=a2,A3A4=a3,…,AnA1=an，其周长为p，绳套的长度为l.

①用绳套套此n边形，得到的轨迹是一个由2n段椭圆弧构成的“果圆”；

②凸n边形A1A2…An的n条边所在直线把平面恰好划分出2n个无限区域；

③当l充分大(或l远大于p)时，“果圆”的各段椭圆弧恰好落在上述2n个无限区域；

④若凸n边形A1A2…An的n条边所在直线没有任何2条是平行的，且l充分大(或l远大于p)，则“果圆”的各段椭圆弧恰好两两成对地落于对角形的无限区域内(共n对)，这成对的椭圆弧具有相同的焦点但长轴长不同，其上的点套住的n边形顶点数之和为n+2.(如，图5中区域A1BFF2与区域A2DEE2就是位于对角形的一对无限区域，其他类似)

(6)空间推广

在(5)中，把“n个点构成凸n边形”改为“n条平行线构成凸n直棱柱面”，“绳套”改换成“带面”，类似地，也可得到相应的结论，此处不一一赘述.

约定：“带面”就是柔软而没有弹性的圆柱面.“带面”的周长大于凸n直棱柱面的周长，否则套不上去.

用“带面”去套凸n直棱柱面得到的轨迹是由2n片椭圆弧面构成的曲面，它也是柱面，我们不妨称之为“果圆柱面”.

3 进一步研究的展望

本研究得出的结论主要利用GeoGebra实验探究得到的，某些关键结论还缺少严格的演绎证明，这是我们后续要做的研究.

本研究提出的“果圆”与“果圆柱面”是否还有其他的一些深层次性质，也是进一步研究的课题.

我们认为，“果圆”与“果圆柱面”在工业设计中肯定有用，比如产品可以设计成这种形状等，它们在生产、生活和科学研究中的其他用途，也值得我们去探索和挖掘.

1 陶维林. 几何画板实用范例教程(第3版)[M]. 北京：清华大学出版社，2013：183-187

2 刘胜利. 几何画板课件制作教程(第3版)[M]. 北京：科学出版社有限责任公司，2016:95-105

3 郑观宝. 一道中考压轴题的实验探究与推广[J]. 中学数学教学，2016(5)：58-61

4 刘秀梅. 用几何画板辅助数学分析教学的策略研究[J] . 数学教育学报，2008(4)：97-101

5 周洪. 主题数学动画的几何画板制作与设计 [J]. 数学通报，2015(12)：45-48

6 左晓明，田艳丽，贠超 . 基于GeoGebra的数学教学全过程优化研究[J] . 数学教育学报，2010(01)：99-102

合肥师范学院2016年重点课题(项目编号：2016JCJY07)，合肥师范学院2017年研究生创新基金项目(项目编号：2017YJS11)

2017-02-06)