圆形磁耦合截面构建的新型时栅位移传感器*

王阳阳,陈锡侯,索龙博,汤其富(重庆理工大学机械检测技术与装备教育部工程研究中心,重庆 400054)



圆形磁耦合截面构建的新型时栅位移传感器*

王阳阳,陈锡侯*,索龙博,汤其富
(重庆理工大学机械检测技术与装备教育部工程研究中心,重庆 400054)

现有磁场式时栅位移传感器暴露出机械加工齿槽等分性差和线圈绕制参数一致性差,导致耦合磁场形成的电信号质量较差的问题。针对以上问题,提出了一种以圆形截面铁磁材料替代传统类矩形截面铁磁材料构建耦合磁场形式的传感器设计方法,该方法采用标准件作为基本阵列导磁单元,并以定制的精密线圈绕组设计一种新型的变磁阻式时栅位移传感器。文中首先利用有限元软件ANSYS Maxwell对理论模型的可行性进行了仿真验证,然后通过精度实验获取了误差范围在±1.3″内的误差曲线,仿真与样机实验验证了新型传感器设计方案的可行性。该方法的应用规避了传统的线切割开槽绕线的机械加工形式,可以在有效提高电信号质量的同时大大提高了时栅的生产效率,有利于时栅位移传感器产品化进程的推进。

时栅位移传感器;变磁阻;圆形截面;磁场耦合

在现代工业中,传感器作为测量基本部件被广泛应用于位移量测量和精密定位中;其要实现的高精度位移测量是精密加工、数控系统、直线伺服电机、计量测量以及国防军工等众多工业应用领域中的一项非常重要的技术[1-2]。其中,应用比较广泛的诸如:光电编码器、磁栅、容栅等多采用基于空间精密刻划的机械制造工艺实现产品的精度保障[3-5]。以国内外应用最广的德国海德汉光栅编码器为例,其精度在±5″至±0.4″范围的产品,线数通常为9 000线～180 000线,精度的实现很大程度上依赖刻划精度和水平。鉴于我国机械加工水平较低的事实,以及在精密刻划工艺方面存在严重的技术短板,国产高精度光栅的研制实现较难,为规避这一技术难题,一种基于“时间量测量空间量”思想[6-8]的新型位移传感器——时栅位移传感器被研究试制。通过时栅研发团队十几年的技术积累,在多项国家自然基金项目的支持下,时栅位移传感器实现了从无到有,从“粗”到“精”的变化。然而,随着时栅位移传感器产品化进程的不断推进,各合作单位相继对时栅的高速度、高精度测量提出了需求。在文献[9-11]中对时栅位移传感器分别开展了相关研究,通过归纳发现作为其基础研究对象的传感器均存在着:整周开槽等分性差和线圈绕制困难及参数一致性差的问题;传感器定、转子之间的耦合面积为类长方形,由此形成的信号波形为三角波的形式,而非希望的正弦波形式,影响了对传感器位移量的精确解析的问题。因此,如何解决上述制约时栅位移传感器产品化的关键问题,是当前时栅产品研发团队面临的一项重要考验。本文拟通过构建一种圆形的磁耦合截面来解决信号波形正弦性差的问题,通过采用标准件滚针作为基本磁导单元,一方面可以确保各个磁导单元的一致性,另一方面也可以构建出正弦性较好的信号波形,提高传感器位移解算精度;装配式的结构也可以解决线切割等加工工艺下加工效率较低等问题。

1 原理及模型

1.1 测量原理

为了建立起时间量测量与空间量测量的关系,文献[6]对时栅位移传感器的测量原理进行了进一步的阐述。通过引入一个相对匀速运动的坐标系将位移量可以分别从时间和空间两个角度进行描述,实现了将一个坐标系上的空间位移测量转换为另一个坐标系上的时间测量,即使得时钟脉冲具备了空间的意义,如式(1),进而通过后续参数设计可实现时栅位移传感器的测量模型。

(1)

式中:Px为离散化的位移;Pt为离散化的时间脉冲;Va为总时间脉冲下平均速度。

磁场式时栅位移传感器,通过构建一个时间正交与空间正交的磁场,利用“电—磁—电”的转换过程将磁场变化转换成电信号量与位移的映射关系来实现测量。假设两相激励源在传感器感生出的有效磁通量分别为φ1和φ2,为了实现磁通量在时间和空间上的正交,构建磁通量的函数形式如式(2)所示:

(2)

上式根据法拉第定律,经过求导运算,对产生的感应电动势可以表述为:

(3)

式中:令k=-Aω,对式(3)中的两路信号进行叠加,获得的电信号量与位移量的关系可表述为式(4)的形式:

E(t,x)=ksin(ωt)·sin(ηx)+kcos(ωt)·cos(ηx)

(4)

式中:ω为磁场的速度;Η为位移量变化速度;K为常数。

工作过程中,传感器将被测位移调制到一个如式(4)形式的正弦信号的相位,如式(5)所示。然后,进一步对该正弦信号按照如图1所示的方法进行解析,得到被测位移量。

E(t,x)=kcos(ωt-ηx)

(5)

为了获取式(7)中的位移量信息,在时空坐标转换的思想基础下,以一组以时间为变量的信号Sr作为参考信号,将E(t,x)与之做比较大大简化处理流程。传感器的信号先后经过:低通滤波、放大处理、过零比较、模数转换等处理过程,获取输出的方波信号SO。位移量发生改变时,SO和Sr信号发生相对变化,以二者的上升沿/下降沿时刻为检测对象,两者上升沿/下降沿到来时刻的时间差Δt便于被测位移对应。被测位移量与时间差Δt之间的关系可表示为式(6)的形式:

x=(n+Δt/T)·xO

(6)

式中:T为参考信号Sr的周期,n为方波信号So在测量范围内变化的周期数,xo为周期T对应的位移量。

1.2 物理模型和数学模型

传统的磁场式时栅位移传感器其结构形式如图2(a)所示。机械结构上其主要由定、转子及按特定方式绕制的线圈绕组所构成;制造工艺方面其主要采用线切割电腐蚀等分开槽的形式进行加工。由于,线切割机电腐蚀加工存在着诸如:加工效率低、机械等分性差、表面成型质量差等工艺弊端[12-13]。因而,本文提出了一种基于标准滚针均匀排列方法所构建的新型时栅位移传感器,其结构形式如图2(b)所示。

图2 两种磁场式时栅模型示意图

标准滚针构建的磁场式时栅,在机械结构方面采用加工一致性好、精度等级高的标准滚柱滚针替代传统齿槽加工;选用定制的精密线圈绕组代替粗糙的手动绕线工艺;借鉴磁阻式旋转变压器的工作机理[14-15],通过信号叠加的方法将已经构建的两路关于时间变量t和空间变量x的拍频驻波合成所需电行波信号。在图2(b)中,为底层定子上的空间正交的线圈绕组分别施加两相正交的正余弦交流激励信号,进而构成空间和时间上的双重正交。通过转子位置的变化,在定、转子之间产生一个随激励信号变化的空间磁场。随着转子位置的变化定子上感应线圈中磁通量变化形式发生相应改变。在对应的感应线圈中将感生出两个相同频率的时间正交信号,对两路信号进行叠加合成出包含着转子位置信息和时间信息量的电行波信号,再通过图1所示解析方法实现位移测量。在文献[16]和文献[17]中分别对时栅的波动方程和行波产生进行了清晰的阐述,其公式如式(7)所示。

(7)

当给两相激励线圈分别通入sin(ωt)和cos(ωt)两路正交信号时,对两路信号进行叠加处理,在图2所示的定子感应线圈中,合成总的感应电动势输出信号将产生式(8)所示:

E=Ki·sin(ωt-pθ)

(8)

式(7)和式(8)中:N1,N2为激励和感应线圈匝数;Λ为气隙磁导;P为传感器对极数;θ为角位移量。

1.3 磁耦合面积分析

本文中提出的磁场式时栅,其定转子在相对运动过程中,在同一投影平面内二者之间的滚针截面耦合变化如图3所示,通过数学推导可以将其耦合面积S耦合,进行如式(9)的表述,在式中最后耦合面积的影响因素主要由夹角α决定。

(9)

图3 同一投影平面定转子耦合示意

传统的磁场式时栅位移传感器和标准滚针为实现载体的圆耦合面积型时栅其安装形式如图2所示,在圆周运动过程中,定、转子单元间磁场的面积耦合变化表现为图4(a)的形式。

图4 耦合面积耦合示意及其变化波形曲线

图7 模型仿真输出信号曲线

为了更加直观的获取两种形式耦合面积变化的对比,假定传统磁场式时栅位移传感器耦合面为边长是4 mm的正方形,而本文设计的标准滚针截面直径也为4 mm,则通过等间隔计算不同位置下定、转子磁场耦合的面积,可以得出其面积变化如图4(b)所示。由式(6)可知,传感器定、转子间耦合面积变化理想上为正弦形式。然而,传统的磁场式传感器相应的耦合面积变化呈三角波形式,与正弦形式有一定差距,而新型传感器相应的耦合面积变化与正弦形式相近。另外,在实际的传感器设计过程中,对于相同的对极数要求,与这种采用标准滚针阵列的新型时栅相比,传统磁场式时栅定转子其齿槽需要加工更小才能达到对极数要求。因此,由气隙磁导公式可以知道耦合面积的大小决定了磁场强度的强弱,本文提出的新型传感器结构在理论上其电行波信号强度更好。另一方面,由于标准件滚针的加工一致性等工艺因素其工作截面相较于类矩形开槽加工的耦合截面一致性更好,对于原始精度的保证更具优势。

1.4 仿真模型

为了进一步验证所构建的时栅位移传感器模型的正确性,采用三维设计软件Unigraphics NX和有限元分析软件ANSYS Maxwell对传感器模型进行仿真实验。通过导入Unigraphics NX所建立的三维立体模型,对其进行诸如:求解类型设置、材料属性定义、激励设置、绕组方向设定、网格划分、施加边界条件等一系列设置。仿真模型YZ平面视图如图5所示,主要由定、转子、作为定转子组件的标准滚针、感应线圈及两相时空正交的激励线圈所组成。其中,定转子的滚针齿数比例为4∶5,且分别在圆周上等间隔布置;感应线圈采用逐齿反向绕制,激励线圈则构建空间正交的布置方式,如图6所示。该仿真模型中,定转子的滚针半径皆为1 mm,齿数安装4∶5的形式在同一直径尺寸均匀分布,滚针长度为3 mm。

图5 仿真模型示意图

图6 定转子绕组形式

1.5 仿真验证与分析

在仿真设置中,通过为传感器施加一相信号幅值为5 V、频率为400 Hz的正弦激励,获取系列感应信号曲线,如图7(a)所示,在图7(b)中给出了单相激励作用下电压幅值变化曲线,其与图4(c)的变化趋势一致,通过与文献[11]中场式时栅感应信号幅值变化曲线的对比,显示其正弦特性更好。在图7(a)中,输出的感应信号幅值变化区间在±150 mV之间,幅值变化形式如图7所示,可见其正弦性与理论分析结果比较接近。另外,在为传感器施加正交的两相激励后,感应信号输出一系列幅值相近,相位随位移变化的曲线,如图7(c)所示。理论上,感应信号输出的曲线相位应与设置的转子角位移呈线性关系。从图7(d)中相位变化Δθ,通过比对发现其变化比较均匀,说明其与转子角位移间的线性关系较好。另外,通过傅里叶分析对图2(a)中的传统场式时栅感应电压与图7(b)中的感应信号进行傅里叶分解,获取图8所示的结果,两种传感器中的三次误差成分尤为明显,分别占其基波幅值的8.6%和17.5%。其中,各奇次谐波成分的对比中,采用圆形截面积的新型时栅其抑制奇次谐波的效果更为明显,可以有效提高传感器原始信号的质量。

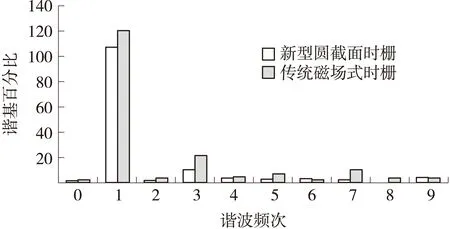
图8 两种不同制式时栅FFT频谱分析

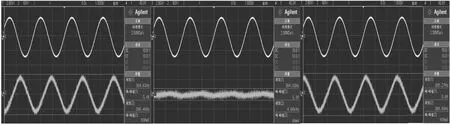
图10 3种不同时刻驻波信号波形

2 实验验证

2.1 传感器结构

根据仿真实验设计的原理样机如图9(a)所示,其中,定、转子按照4∶5的齿数比例均匀布置滚针排列,滚针数量分别为72和90,其余参数见表1。在定子层上为滚针嵌套定制的两相正交激励绕组及感应绕组,线圈绕组的方向及连接由PCB串接板实现。

表1 传感器参数

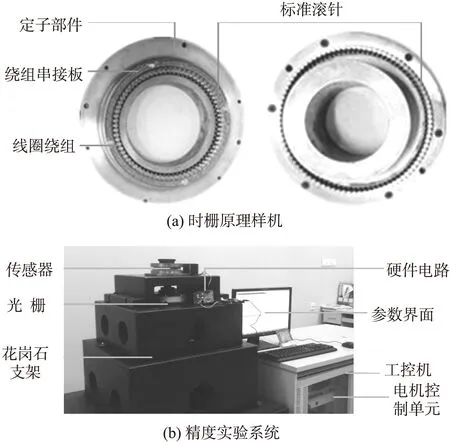
图9 精度标定实验系统

2.2 驻波与行波信号测试

传感器的驻波形成实验根据标准件构建的新型时栅传感器原理,利用两路驻波合成一路行波的方法得到所需的测量信号。通过为激励线圈施加单相激励信号,同时转动转子并用示波器抓取感应信号的变化情况,如图10所示,其中,上端的黄色信号波形曲线为输入的参考激励信号,绿色曲线为实际感应出的驻波信号。伴随着转子的运动,在一个对极内,感应信号的幅值变化由正的最大变为零,再变到负的最大,其变化规律符合驻波的变化情况。

行波信号的验证实验是在驻波实验的基础上进行的,为获取最终测量所需的行波信号,需要为传感器定子激励线圈施加两路相位相差90°的激励信号。用示波器观察行波信号的变化情况,随着转子的转动行波信号的变化情况,由图11所示,黄色曲线为A相激励信号,绿色曲线为不同时刻的感应行波信号。由图11可以看出在不同时刻,随着子的转动,行波信号在时间轴上进行移动,相位发生变化。

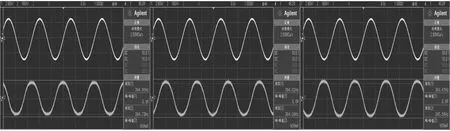
图11 3种不同时刻信号波形

图12 采样误差数据曲线

2.3 精度实验

精度验证实验在图9(b)所示的实验台系统上进行,该实验系统主要包括:作为测量基准的光栅、硬件电路、测试软件参数设置模块、工业计算机、电机及控制系统等。在精度实验过程中,电机控制单元控制直驱电机带动同轴安装的光栅和待测传感器的转子同步运动,硬件电路将光栅和被测传感器的测量数据同步采集,并发送至计算机中进行记录和处理。

实验系统中采用标称精度为±1″的德国海德汉RON886型光栅作为测量母仪,先后对新型传感器开展整周(0°～360°)范围的一系列动态实验。传感器的原始测量误差如12(a)所示,其误差具有周期重复性,单个周期误差如图12(b)所示。通过将传感器的测量误差在软件中进行修正,最终新型传感器的测量精度在整周测量范围内可以达到±1.3″以内。

3 结论

本文提出了一种基于圆磁耦合截面构建传感的方法,并采用了常用的标准件滚针作为基本陈列元件。另外,文中对新型的时栅角位移传感器的测量原理进行了阐述,并开展了模型建立、仿真工作及精度验证实验。通过仿真实验、波形验证实验及精度实验对该传感器设计参数进行了验证,通过对整周范围内信号变化的周期的分析,其符合磁场式时栅的输出特性。通过误差修正技术,误差成分中含有的一次和二次谐波成分可以有效的进行抑制,减少椭圆和偏心引起的测量误差。

应用标准件滚针所构建的圆形磁耦合面基本阵元的新型时栅位移传感器,较开槽绕线工艺加工的磁场式时栅位移传感器在对极一致性、等分性、信号正弦性、谐波成分减少等方面皆有所提高。同时,因其摒弃了线切割加工开槽和人工绕线的工艺,使得传感器的加工效率大大提高,进而降低了传感器的制造成本,为时栅位移传感器的产品化提供了一个新的设计思路。

[1] Aschenbrenner B,Zagar B G. Planar High-Frequency Contactless Inductive Position Sensor[C]//IEEE International Instrumentation and Measurement Technology Conference. 2013:614-619.

[2] 武亮,陈锡候,王阳阳,等. 磁导调制型时栅位移传感器测量方法研究[J]. 传感技术学报,2014,27(8):1043-1048.

[3] Wu S T,Chen J Y,Wu S H. A Rotary Encoder With an Eccentrically Mounted Ring Magnet[J]. IEEE Transactions on Instrumentation and Measurement,2014,63(8):1907-1915.

[4] 李晓天. 机械刻划光栅刻线误差及其修正方法研究[D]. 中国科学院研究生院(长春光学精密机械与物理研究所),2013.

[5] Gao W,Kim S W,Bosse H,et al. Measurement Technologies for Precision Positioning[J]. CIRP Annals-Manufacturing Technology,2015,64(2):773-796.

[6] 彭东林. 时栅位移传感器与新型机床动态检测系统[M]. 北京:科学出版社,2009.

[7] 陈锡侯. 新型时栅位移传感器研究[D]. 重庆:重庆大学,2007.

[8] 彭东林,练俊君,陈锡候,等. 基于时间序列的时栅转台误差修正研究[J]. 重庆理工大学学报(自然科学版),2015,29(1):96-100.

[9] 汤其富,彭东林,武亮,等. 时栅角位移传感器中的多普勒效应影响及其抑制方法研究[J]. 仪器仪表学报,2014,35(3):620-626.

[10] 高忠华,陈锡侯,陈鸿雁. 寄生式时栅传感器自标定方法研究[J]. 仪器仪表学报,2015,36(5):975-981.

[11] 张天恒,李志明,杨继森. 基于参数辨识的时栅转台在线自动标定系统[J]. 传感技术学报,2016,29(3):462-466.

[12] 李丹,张春华. 多轴联动功能的电火花线切割机床方案设计与实现[J]. 航空制造技术,2014(16):38-41.

[13] 胡选利,唐永杰. 线切割机电极丝动态稳定性的主动控制研究[J]. 振动工程学报,1995(1):815-815.

[14] 邢敬娓. 新型磁阻式旋转变压器相关问题研究[D]. 哈尔滨:哈尔滨工业大学,2007.

[15] 强曼君. 磁阻式多极旋转变压器的误差分析[J]. 微特电机,2000,28(1):9-12.

[16] 彭东林,陈锡侯,朱革,等. 时栅的波动方程分析与行波形成新方法[J]. 机械工程学报,2006,42(11):39-43.

[17] 杨伟. 时栅的波动方程分析与行波形成新方法的研究与实验[D]. 重庆:重庆大学,2006.

王阳阳(1986-),男,吉林农安人,重庆理工大学精密仪器及机械专业硕士研究生,主要研究方向为智能仪器设计及精密测量技术,why_go@163.com;

陈锡侯(1975-)男,福建漳州人教授,先后于2004年、2007年获得重庆大学硕士学位和博士学位,现为重庆理工大学教授,主要研究方向为精密测量与智能传感器,cxh0458@163.com;

索龙博(1988-),男,陕西宝鸡人,硕士研究生,主要研究方向为计算机辅助测试技术与仪器,546393674@qq.com。

A Novel Time-Grating Displacement Sensor Based on the Circular Magnetic Coupling Cross Section*

WANG Yangyang,CHEN Xihou*,SUO Longbo,TANG Qifu
(Engineering Research Center of Mechanical Testing Technology and Equipment,Ministry of Education, Chongqing University of Technology,Chongqing 400054,China)

There exist some problems on the current magnetic-field time-grating displacement sensor,such as the unequal interval of tooth and slot,the inconsistent parameters of coils and the poor quality of electrical signals formed by the coupling magnetic field. To solve the above problems,a new method to design sensor is presented that it uses the ferromagnetic material with a circular cross section to replace the traditional ferromagnetic material with rectangular section to build the coupling magnetic field. The method adapts the standard parts as the basic array permeability units,supplemented by customized precision winding to design a new variable reluctance time grating displacement sensor. Firstly,the feasibility simulation of the theoretical model is verified by the finite element software ANSYS Maxwell. Then,the error curve of error range within±1.3 arc-sec is obtained by the precision experiment. The simulation and practical experiments verify the feasibility of new sensors. The application of this method evade the mechanical processing form of slotting by traditional linear cutting and wiring,greatly improve the quality of output signal and production efficiency,at the same time is good to promoting the transition progress of the time grating sensor.

time-grating;circular cross section;variable reluctance;coupling magnetic field

项目来源:国家自然科学基金项目(51605062,51675071);重庆市研究生科研创新项目(CYS15218);重庆市教委科学技术研究项目(KJ1600940)

2016-09-21 修改日期:2016-11-28

TP216

A

1004-1699(2017)04-0512-07

C:7230

10.3969/j.issn.1004-1699.2017.04.005