基于边缘电场传感器的大范围位移测量方法
王文霞,王文廉*(1.中北大学仪器科学与动态测试教育部重点实验室,太原 030051;2.中北大学电子测试技术重点实验室,太原 030051)
基于边缘电场传感器的大范围位移测量方法
王文霞1,2,王文廉1,2*
(1.中北大学仪器科学与动态测试教育部重点实验室,太原 030051;2.中北大学电子测试技术重点实验室,太原 030051)
主要研究基于边缘电场传感器的位移测量方法,由于在测量位移时交叉指型传感器互导电容的变化具有周期性,因而可以实现大范围的位移测量。运用Ansoft Maxwell有限元仿真软件对边缘电场传感器的二维半波长模型进行了仿真分析,仿真结果表明当传感器工作区间内有物体移动时,会改变传感器的电场分布,使传感器互导电容发生周期变化。设计了一个简单的、低成本的调理电路,可以将电容变化转化为电压输出信号,得到边缘电场传感器输出电压与电容的关系。对电极尺寸为35 mm×30 mm×0.02 mm的边缘电场传感器进行了测量实验,实验结果与仿真结果吻合较好。
边缘电场传感器;有限元;互导电容;调理电路
TP212边缘电场传感器FEF(Fringing Electric Field Sensors)通过测量电容值获得所需物理量,如介电常数、含水量、粘度、液位、位移等。边缘电场传感器属于电容传感器,相当于将平行板电容器的两极板展开置于同一平面内,在两极板平面的上方构成工作区间。与传统的平行板电容式传感器相比,边缘电场传感器的电力线分布呈散射状,电场能集中在电极附近,同时也具有单边穿透、信号强度可调以及层析成像等优点,被广泛用于物体物理特性的非接触测量[1]。
FEF传感器一直是国内外学者研究的热点,对边缘电场传感器的研究主要集中在传感器的设计、参数估计算法的实现,测量系统的设计与应用等方面。德国雷斯顿工业大学设计了用于快速多相流体成像的FEF传感器测量系统,将交流电容测量电路与介电常数转电压电路结合,使用对数放大器解调交流电容来测量电路输出,得到了电压输出与介电常数之间的关系[2]。爱尔兰列墨瑞克通过在FEF传感器电极上涂二氧化钛涂层来测量传感器表面的压力,使用CMOS振荡电路将传感器电极间的电容值转换为振荡频率变化,再利用PLL电路将振荡频率变化转变为直流电压变化进行测量,建立了传感器输出电压与压力的关系[3]。泰国玛哈沙拉堪府大学使用信号发生器产生驱动信号并用调理电路缓冲,使用力科LT354数字示波器测量调理电路输出电压,设计了边缘电场传感器测量系统,并结合边缘电场传感器对水中糖分含量进行了测试,建立了调理电路输出电压和水中糖分的关系[4]。太原理工大学窦银科等人设计了基于叉指传感器的冰层厚度测量系统,系统以飞卡尔MC9S12x为处理运算的核心,外部提供正弦驱动信号,实验有效[5]。然而,边缘电场传感器在位移测量方面的研究少之又少,台湾国立云林科技大学选择同心环型边缘电场传感器为研究对象,对一个目标的短距离变化进行了测量,调理电路将传感器微小位移转换成电压输出,测量精度高达亚微米级别[6]。目前,国内外还没有学者将边缘电场传感器用来进行大范围位移测量方面的研究。
本文在分析边缘电场传感器测量位移基本原理的基础上,得到了传感器互导电容值与位移的关系。运用Ansoft Maxwell有限元仿真软件对其二维半波长模型进行了仿真分析,设计并制作了一个调理电路,可以将传感器互导电容转换成电压输出信号,得到了输出电压与电容之间的关系。通过实验数据和仿真数据的对比,进一步验证了边缘电场传感器可用于大范围位移测量。
1 边缘电场传感器位移测量原理
本文选择交叉指型电极结构的边缘电场传感器为研究对象,交叉指型传感器由驱动电极和感应电极组成,两电极交叉分布,同行电极间的距离相等,能够改善电场分布,增大电容值。当在传感器的驱动电极上施加一定频率的电压信号VD时,则在感应电极上产生感应电压VS,通过测量电压VS并结合传感器的等效电路模型,可以求出驱动电极和感应电极之间的互导电容值。当被测金属目标进入传感器的工作区间后,由于被测金属目标在金属电极间电场中的位置不同,穿过电力线的疏密程度不同,因而引起电容量的变化不同,虽然电容量的这种变化与位置变化之间具有一定的非线性,但可通过选取线性工作区域和非线性矫正来减小[7-9]。根据电容值的变化规律,以及传感器空间结构周期分布的特点,通过对调理电路的电压输出幅值进行检波就可以得到物体移动的距离。边缘电场传感器位移测量原理如图1所示。其中,驱动电极D和感应电极S的长均为L,宽为a,两电极相距为b。被测目标W长为a,与传感器间距为d。x1和x2分别为目标物体在X方向移动时与两电极覆盖的横向位移。
将交叉指传感器的半波长物理模型简化后可以得到其等效电路模型,如图2所示。

图1 边缘电场传感器位移测量原理图

图2 交叉指传感器半波长等效电路模型
图2中,VD为传感器驱动电压,VS为传感器感应电压,C12和G12分别是传感器两极间的电容值和电导值,C10和G10分别为传感器驱动电极与被测物体间的电容值和电导值,C20和G20分别为传感器感应电极与被测物体间的电容值和电导值。则传感器的互导电容值为
(1)
(2)
(3)
而
x1+x2+b=a
(4)
(5)
式中:ε为工作区间的总介电常数。当目标物体W由右至左做单方向移动时,互导电容值C总随着x1的变化而变化。由于边缘电场传感器的空间结构分布具有周期性,所以目标物体在边缘电场传感器工作区间移动时,引起传感器互导电容的变化具有周期性,使得边缘电场传感器能够应用于大范围位移测量。
2 有限元传感器仿真

图3 不同位置下边缘电场传感器电场分布图
在Ansoft Maxwell中建立边缘电场传感器的二维半波长模型,设驱动电极与感应电极的电极长均为35 mm,厚度为0.02 mm,材料属性设置为aluminium,两电极相距2 mm。被测物体长35 mm,厚9 mm,材料属性为tin,与传感器的垂直距离为0.042 mm。分别将驱动电极、感应电极和被测物体命名为D、S、W。将驱动电极的电压设置为1 V,感应电极的电压设置为0 V。模型的左右边界设置为even,即偶对称,表示电极在x轴上是无限周期分布的,模型的上下边界设置为气球边界条件Ballon,可以减小内存和CPU等计算资源的开销。仿真中收敛误差设置为1%。目标物体在电极系统工作区间内单方向移动时,以2 mm位单位间隔,仿真范围为36 mm,仿真其电场分布情况,并求解不同位置下电极系统的互导电容值[10-11]。
图3(a)为边缘电场传感器本身的电场分布图,此时的互导电容值为12.65 pF;图3(b)是当目标物体移动到感应电极正上方时的电场分布图,此时目标物体基本不影响传感器的电场分布,其互导电容为19.607 pF;图3(c)是当目标物体移动到传感器工作区间的正上方位置时的电场分布,此时互导电容值最大,为1779.2 pF;图3(d)为目标物体移动到驱动电极正上方时的电场分布,此时互导电容值与图3(b)相差较小,为17.445 pF。
将不同位置下传感器的互导电容值绘制成图,其变化规律如图4所示。
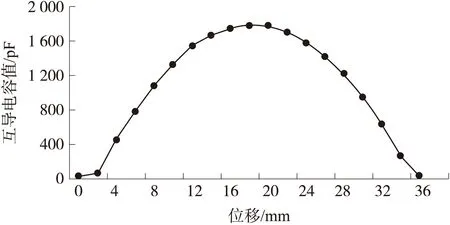
图4 传感器互导电容值随位移变化曲线图(仿真)
由图4可以看出,目标物体移动到两电极的中间位置时,互导电容值最大,目标物体位于电极两侧时,互导电容值近似对称,此变化规律符合式(5)的推导。故物体在传感器工作区间内移动时,互导电容值呈周期变化。
3 传感器调理电路设计
传感器调理电路由脉冲信号发生器,两组平行的电容电压转换器和一个仪表放大器组成,如图5所示。脉冲发生器LM555输出一个10 kHz的方波信号,用于激励传感器。传感器的核心由双并联电容-电压转换器构成[12],这两组电容电压转换器由参考电容C3,检测边缘电容C4,双套整流器和两组过滤器构成,其后是一个仪表放大器INA122,其电压输出用来确定边缘电容C4的变化量,进而探测物体位移量。
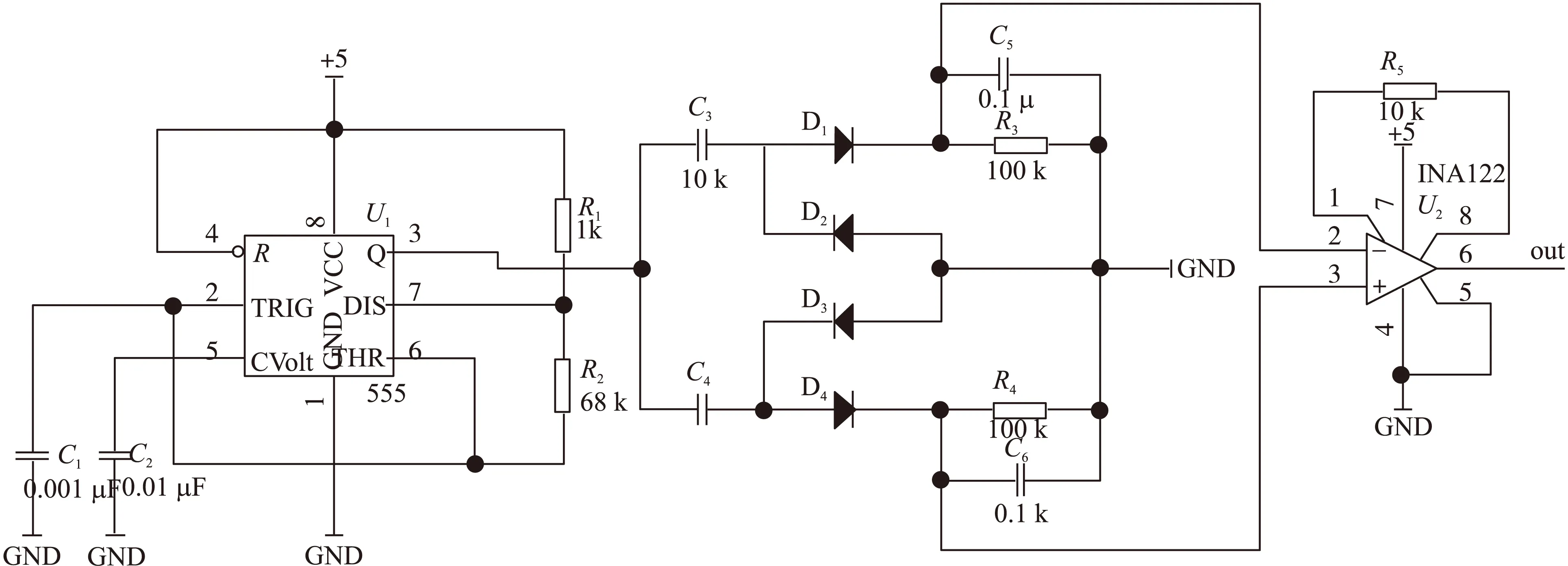
图5 调理电路原理图

图6 调理电路实物图
脉冲发生器LM555产生一个稳定的方波信号对两个电容进行充放电,通过整流器和滤波器后,输出的两个AC电压就被转换成了DC电压,这两个DC电压相比较后得到一个电压差值,而这个电压差值对应于边缘电容的感应值。当目标物体在边缘电场传感器的工作区间移动时,传感器互导电容就会发生变化,相应的输出电压,且输出电压与传感器互导电容成正比,即
UO=K(C4-C3)
(6)
为了验证调理电路的可行性,用其对不同的电容进行测量,得到输出电压与电容的关系如图7所示。

图7 调理电路输出电压与电容值的关系图
由图7可以看出,调理电路输出电压与电容的关系近似为正比,且其关系式为
y=0.064 7x-0.853 3
(7)
4 实验及结果分析
用铝箔纸设计了边缘电场传感器的一个半波长模型,驱动电极和感应电极的长均为35 mm,宽为30 mm,厚度为0.02 mm,两电极相距2 mm,被测目标选用35 mm×30 mm×9 mm的量块,测量实验如图8所示。实验时,使其在边缘电场传感器上方做单方向移动,测量的总范围为36 mm,以2 mm为单位间隔,用电容表记录不同位置下边缘电场传感器的互导电容值。将得到的实验数据绘制成表,如图9所示。

图8 测量实验图

图9 传感器互导电容值随位移变化曲线图(实验)

图10 传感器互导电容值随位移变化曲线图(仿真修)
由于仿真结果针对的是边缘电场传感器的二维半波长模型,无法与实验结果进行直观的比较,所以需要将图4所示的数据进行处理。设二维仿真的互导电容值为C1,三维仿真的互导电容值为C2,则有
(8)
即
C2=0.03C1
(9)
经处理后得到了如图10所示的曲线。由图9和图10对比可以看出,由于传感器表面不平整、传感器与被测物体中间有空隙以及测量误差等原因导致实验结果与仿真结果存在一定的误差,这可以通过采用薄膜制作工艺,改进测量手段,提高测量精确度等得到很大改善,总体而言,实验结果与仿真结果吻合较好。由于本文的研究对象为边缘电场传感器的一个半波长模型,而边缘电场传感器空间结构呈周期分布,所以边缘电场传感器在测量位移时得到的输出与位移的关系是由若干个上述图线组成的,具有很强的规律性与周期性,能够实现大范围位移的测量。
6 结论
边缘电场传感器在位移测量方面有广阔的应用前景。运用Ansoft Maxwell有限元仿真软件对边缘电场传感器的二维半波长模型进行了仿真分析。通过边缘电场传感器对金属目标进行的测量实验,得到的实验结果与仿真结果吻合较好,进一步表明边缘电场传感器能够实现大范围位移的测量。以上工作为实现大范围位移的动态测量提供了良好的基础。
[1] 黄云志,单开. 边缘电场传感器测量系统的设计与实验[J]. 电子测量与仪器学报,2012(2):161-165.
[2] 黄云志,郑亮,汪蓓蓓. 多波长边缘电场传感器介电测量系统的研究[J]. 电子测量与仪器学报,2015(6):853-859.
[3] Arshak K,Arshak A,Morris D,et al. A Wireless Pressure Measurement System Based on TiO2Interdigitated Sensors[J]. 2005:12-15.
[4] Angkawisittpan N,Manasri T. Determination of Sugar Content in Sugar Solutions Using Interdigital Capacitor Sensor[J]. Measurement Science Review,2012,12(1):8-13.
[5] Chang X M,Dou Y,Zhuo D,et al. Research on Sensor of Ice Layer Thickness Based on Effect of Fringe Electric Field[C]//International Conference on Computing,Measurement,Control and Sensor Network. IEEE,2012:417-420.
[6] Wang D C,Chou J C,Wang S M,et al. Application of a Fringe Capacitive Sensor to Small-Distance Measurement[J]. Japanese Journal of Applied Physics,2003,42(9A):5816-5820.
[7] 郑志敏,丁天怀. 用于非金属目标非接触位置检测的单片式电容传感器[J]. 清华大学学报(自然科学版),2003(2):172-174.
[8] 向莉,董永贵. 同面散射场电容传感器的电极结构与敏感特性[J]. 清华大学学报(自然科学版),2004(11):1471-1474.
[9] 黄云志,崔昊旻. 边缘电场传感器建模及逆问题研究[J]. 科技通报,2010(5):708-711.
[10] 张慧凤,黄云志. 边缘电场传感器设计与参数估计算法的研究[D]. 2012:9-14.
[11] 刘国强,赵凌志,蒋继娅. Ansoft工程电磁场有限元分析[M]. 北京:北京电子工业出版社,2005:159-170.
[12] 张丽霞,杨忠华,孙金花,等. 一种电容式传感器信号调理电路的设计[J]. 物探装备,2007(2):79-82.
[13] 黄云志,张慧凤,汪蓓蓓. 多波长边缘电场传感器参数估计算法的研究[J]. 传感技术学报,2013,26(1):63-66.

王文霞(1992-),女,山西朔州人,硕士,研究方向为动态测试与智能仪器,wangwenxia127818@163.com;

王文廉(1978-),男,四川乐至人,电子科技大学博士,现任中北大学副教授、研究生导师。主要从事半导体功率器件、智能仪器等的研究,已发表包括SCI收录论文在内的多篇高质量学术论文,wangwenlian@nuc.edu.cn。
A Large Scale Displacement Measurement Method Based on Fringing Electric Field Sensors
WANG Wenxia1,2,WANG Wenlian1,2*
(1.Key Laboratory of Instrumental Science and Dynamic Measurement(North University of China)Ministry of Education,Taiyuan 030051,China;2.Key Laboratory for Electronic Measurement and Technology(North University of China)Taiyuan 030051,China)
This paper is focused on a displacement measuring method based on Fringing Electric Field Sensors,which can realize a wide range of displacement measurement because of the periodicity in changes of the mutual capacitance of the interdigitated structure in displacement measurement.The two dimensional model of the Fringing Electric Field Sensors was simulated and analyzed by Ansoft Maxwell. The results show that when the target is moving in the working range of the sensor,the distribution of the Fringing Electric Field Sensors will change,resulting in periodic variation in mutual capacitance. A simple and low cost conditioning circuit is designed,which can convert the capacitance to voltage output signal,and then the relationship between the output voltage and the capacitance of the sensor is obtained. Experiments were carried out on the Fringing Electric Field Sensors with the electrode size of 35×30×0.02mm3,and the results were in good agreement with the simulation results.
fringing electric field sensors;finite element;mutual capacitance;conditioning circuit
2016-09-29 修改日期:2016-11-22
TP212
A
1004-1699(2017)04-0506-06
C:7230
10.3969/j.issn.1004-1699.2017.04.004

