基于元胞自动机的激进型驾驶行为换道模型

丁深圳，杨晓芳，王百里

(上海理工大学 交通工程系，上海 200093)

基于元胞自动机的激进型驾驶行为换道模型

丁深圳，杨晓芳，王百里

(上海理工大学 交通工程系，上海 200093)

为研究实际高速路激进型驾驶行为对交通流的影响，对NGSIM中80号州际公路(I80)数据进行分析。通过对数据中车头间距、车辆换道等参数的分析，提出了针对激进型驾驶行为的换道模型。运用元胞自动机，在单车道VDR模型和双车道STCA模型基础之上采用动态换道概率并建立了ISTCA模型。通过对不同道路密度条件下换道行为进行模拟仿真，并与STCA模型进行对比分析。仿真分析表明，在一定密度范围内，ISTCA模型能有效提高道路的通行能力。

交通工程；激进型驾驶行为；元胞自动机；换道模型；双车道

驾驶员的驾驶行为研究作为一个复杂的过程，近年来受到学者们的广泛关注。基于元胞自动机的驾驶行为研究主要分为跟驰行为和换道行为两部分。其中，具有代表性的有Nagel和Schreckenberg提出的NaSch模型[1]和Wolf等人提出的STCA换道模型[2]。NaSch模型为单车道跟驰模型，属于可描述道路交通流基本特征的最小化模型。基于NaSch模型，人们提出了诸多改进模型。例如，为体现亚稳态和回滞现象所提出的TT(Takayasu-Takayasu)模型、Benjamin，Johnson和Hui(BJH)模型以及Barlovic等人提出了依赖于速度的随机慢化模型[3-5]。然而在实际交通中，换道超车现象普遍存在，为模拟更加切合实际的交通，Wolf等人提出了双车道元胞自动机模型(Symmetric Two-lane Cellular Automata，STCA)，该模型把车辆分为快车和慢车两类，从对称性和非对称性换道两个方面进行研究发现，非对称性换道模型更有利于保障快车速度收益[2]。魏丽英等人[6]从换道模型进行研究，结合强制换道模型及自由换道模型，提出了一种综合换道模型，研究了交叉口进口道不同密度下换道率的变化。贾斌等人[7]针对双车道情况下快车激进型驾驶员的换道行为进行研究，提出了改进的STCA模型，研究发现，乒乓换道行为的发生主要原因为快车受到前车的阻挡。Xia Wan等[8]对高速路合流区车辆的横向移动对换道行为的影响研究，提出了横向因素影响下的加减速模型。为研究多车道驾驶员驾驶行为习惯，郑亮[9]在线性稳定理论基础之上考虑了横向摩擦建立模型并获得交通流稳定性条件。钱勇生等[10-11]致力于运用元胞自动机对事故下高速路交通流进行研究，模拟出符合实际事故下的交通流状态。

本文结合实际数据观测分析，针对车辆速度、车辆间距对换道的影响加以考虑，研究激进驾驶员驾驶行为，在STCA模型基础之上对换道规则进行了改进，提出符合实际的元胞自动机换道模型。

1 实际数据分析

为研究激进型换道行为，本文对美国联邦公路局NGSIM(Next Generation Simulation)数据中加州爱莫利维尔市的洲际公路——I 80路段进行分析。道路行驶过程中，当前车道车头间距无法满足需求时，驾驶员会采取换道行为，如图1(b)所示。相邻车间距小于临界间隙的情况下，为保障行车安全，驾驶员一般采取跟驰。但对于激进型驾驶员而言，为达到或保障速度收益，即使前车间距小于临界间隙，只要相对速度等条件满足，驾驶员也会采取换道行为，如图1(a)所示。对于激进型驾驶员，为保障速度收益最大化，即使当前车道车头间距较大，驾驶员也会采取换道行为，如图1(a)中箭头2处所示。

图1 时空轨迹图

如图2(a)所示，与临道前车相对速度较大时，即使与前车车辆间距较小，为达到速度收益，激进型驾驶员采取换道行为。而对于一般型驾驶行为，通常情况如图2(b)所示，在间距较大的情况下采取换道行为。

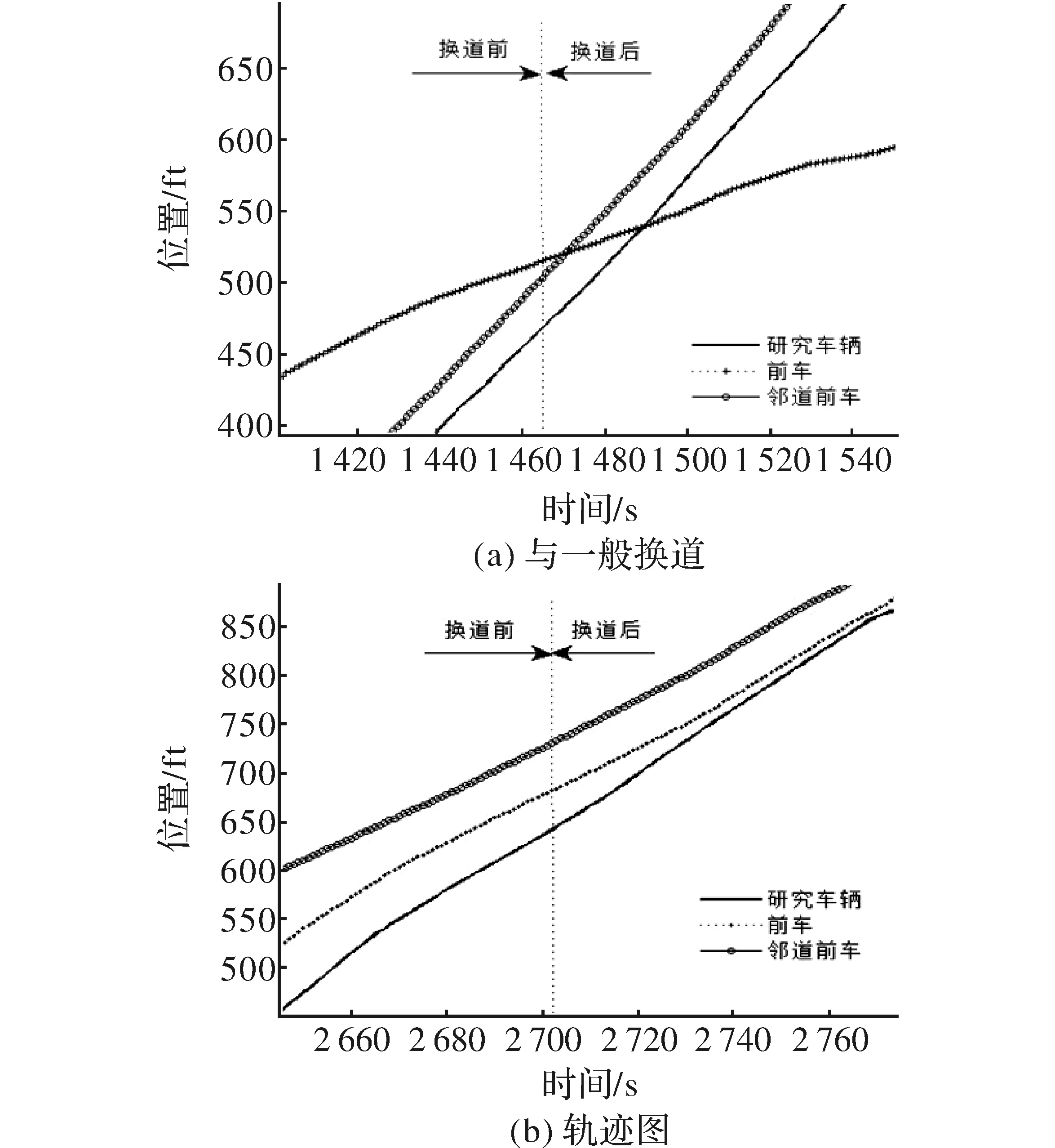
图2 激进型换道

通过对数据中不同车辆间车头间距变化统计分析发现，车辆换道时与前车和后车的车辆间隙大于平均可接受间隙，并且平均可接受间隙大于平均车辆跟驰间隙，如表1所示。

表1 前后车间隙数据统计

另外，根据实际数据统计分析得出，采样研究数据中，换道总次数2 925次。其中，小于可接受间隙的换道次数为491次，占换道总数的16.8%，如表2所示。

表2 换道间隙分析

为进一步研究道路交通中激进型驾驶行为和换道概率对交通流的影响，建立交通模型是必要的。

2 模型

在对道路交通驾驶行为研究过程中，驾驶员换道行为影响因素复杂，传统上从数学模型出发对驾驶行为进行研究，结果理论性较强。元胞自动机具有时间离散、空间离散、分布离散等特性，能较为详尽地描述了道路车辆集结、回滞、消散等交通流现象，在近年来的研究中得到青睐。

为研究道路驾驶员驾驶行为特性，本文采用元胞自动机建模、仿真。根据实际数据分析中所描述的换道行为在元胞自动机中表述如下：

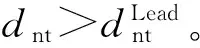
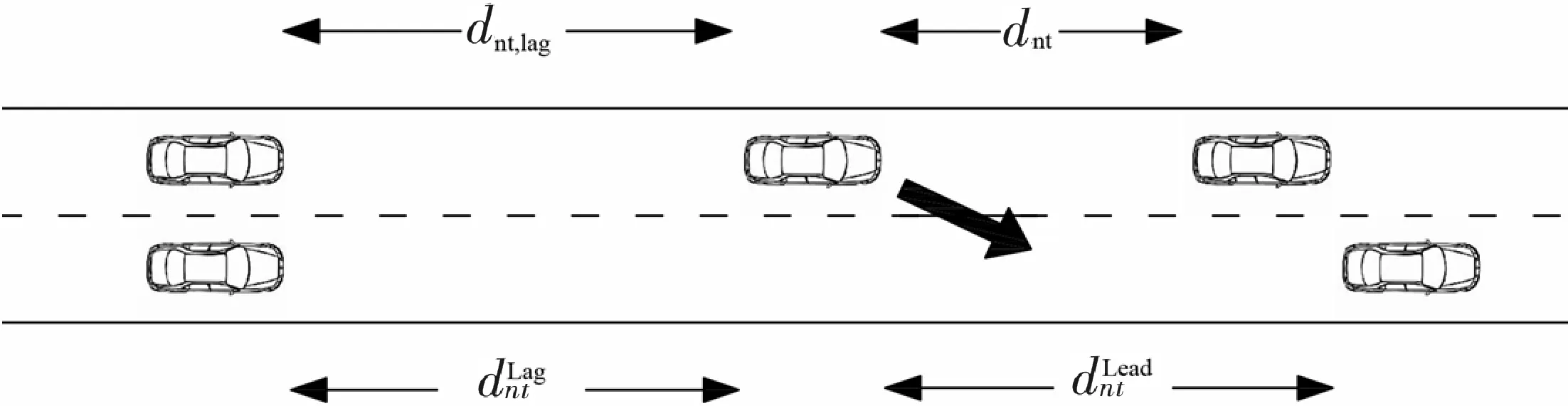
图3 一般驾驶员换道

图4 激进型驾驶员换道

通过对换道间隙分析过程中发现，16.8%的车辆换道小于可接受间隙，图4所示的换道比例为33.9%。然而，以往元胞自动机模型的换道规则设置中，未对该换道现象加以考虑。另外，在实际数据中，如表2所示，驾驶员会在相邻车辆间间距远大于可接受间隙时采取换道措施，以往元胞自动机交通流模型中，仅从前车间距无法满足当前车辆的角度考虑。以上两个问题显然与实际现象有出入。

根据上述分析结果，本文针对不同驾驶行为类型将驾驶员分为两类：一类是倾向于依靠超车、换道以追求速度收益的激进型驾驶员，另一类是倾向于减速、跟驰以保持安全状态的保守型驾驶员。

换道模型研究拆分为两个部分：车辆跟驰和车辆换道。

2.1 跟驰规则

NaSch模型能通过简单的规则设置模拟车辆跟驰状态。但交通流中亚稳态和回滞现象无法表现。为更好模拟符合实际的交通流运行状态，跟驰规则采用随机慢化率随速度变化而改变的VDR(Velocity Dependent Randomization)模型。模型将路段拆分为长度为l的元胞。元胞有被车辆占用或非占用两个状态。每辆车车速为0,1,2,…，vmax。vmax为最大车速。从时间t→t+1过程中，模型按照以下规则演化：

第1步 确定随机慢化率

第2步 加速

vn(t+1)→(vmax,vnt+1)；

第3步 减速，vn(t+1)→min(vnt,dnt)；

第4步 随机慢化，以概率p，vn(t+1)→max(vnt1,0)；

第5步 位置更新，xn(t+1)→xnt+vnt。

其中，vnt，xnt分别指n车的速度和位置；dnt为n车与前车的元胞个数；p为随机概率。

2.2 换道规则

以往元胞自动机换道模型中(以STCA模型为例)，一方面，换道条件仅从相邻车辆间间距出发考虑，对车辆间速度变化，尤其是相对速度变化，没有加以考虑；另一方面，采用固定值的换道概率不符合实际过程中道路交通。本文换道规则以STCA模型为基础进行改良提出了ISTCA(Improved Symmetric Two-lane Cellular Automata)模型。

STCA模型中，换道规则如下

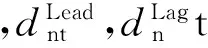
考虑到激进型驾驶行为之后，对STCA模型的换道规则进行改进，增加针对激进型驾驶员的换道规则。改进后换道模型如下

或

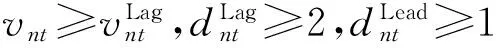
为描述不同类型驾驶员及道路条件下换道概率，模型换道概率设置如式(1)和式(2)所示。

(1)

(2)

其中，CLead/CLag为临道前车/后车换道因子；γlead为临道前车速度影响因子，γlead=1；γlag为临道后车速度影响因子，γlag=1.2；Pnt为车辆n在t时刻激进型驾驶员换道概率。

通过以上换道规则可以看出，对于激进驾驶员而言，当驾驶员产生换道意图，目标车道前车速度与该车速度差加上当前车头间距，如果满足换道所需间距，驾驶员将以概率换道。

3 仿真分析

在仿真过程中主要参数设置如下：车辆慢化率p=0.1，以激进型为代表的快车最大速度vmax1=5，一般驾驶类型的慢车最大速度vmax2=3，快车比例R=0.3，仿真步长simulation_steps=100，道路长度road_length=100(100个元胞)。

3.1 不同模型条件下流量-密度对比

根据以上参数，分别对NaSch模型、STCA模型和ISTCA模型进行仿真运行。得到图5所示流量—密度图。

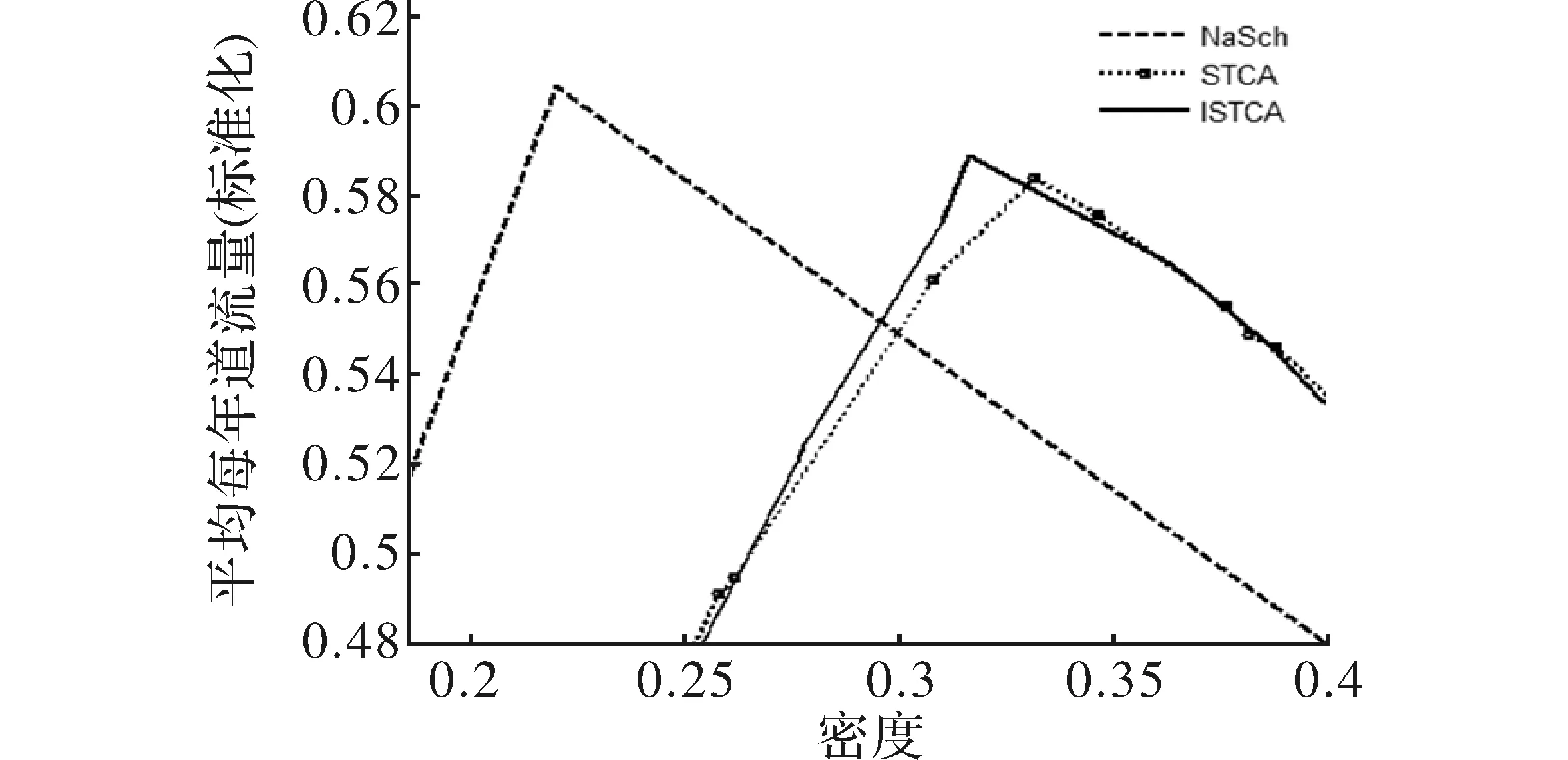
图5 快车比例R=0.3时NaSch、STCA和ISTCA模型流量-密度图

如图5所示，NaSch模型在密度约为0.22时达到最大通行能力，而STCA模型和ISTCA模型分别在密度为0.32和0.34时达到最大通行能力。其原因主要在于，NaSch模型为单车道，与双车道相比，可选取空间局限于本车道，而STCA模型和ISTCA模型中，车辆空间选择性较大，在道路密度增加到一定程度的时候，可以通过换道来获得速度收益。

3.2 换道规则对通行能力的影响

图6为ρ=0.32时STCA模型和ISTCA模型一条车道的时空图。图7给出了不同密度条件下STCA模型和ISTCA模型换道次数。结合图5中流量-密度变化关系所示，在ρ=0.32时，ISTCA模型流量明显大于STCA模型。其原因在于，ρ=0.32时，车辆行车空间受到限制，出现拥挤状态。此时，STCA模型通过相邻车车间距判断换道条件，当条件不符合时，车辆选择跟驰，如图6(a)所示。ISTCA模型通过对车辆间相对速度、车辆间距等条件进行判断，采用灵活的换道概率，在安全范围内，采取相对频繁换道保障速度收益，如图7所示。在当前车道发生拥堵时，能根据道路条件，有效采取换道行为，保障自身速度收益的同时，加快了拥挤消散。因此，该密度条件下ISTCA模型道路拥堵发生频率较小，道路拥堵持续时间相对减少，如图6(b)所示。

STCA模型和ISTCA模型特点对比：

(1)当密度较小时，车辆拥有足够车辆空间自由行驶，换道行为很少发生，STCA模型与ISTCA模型流量基本相同；

图6 STCA模型与ISTCA模型时空图

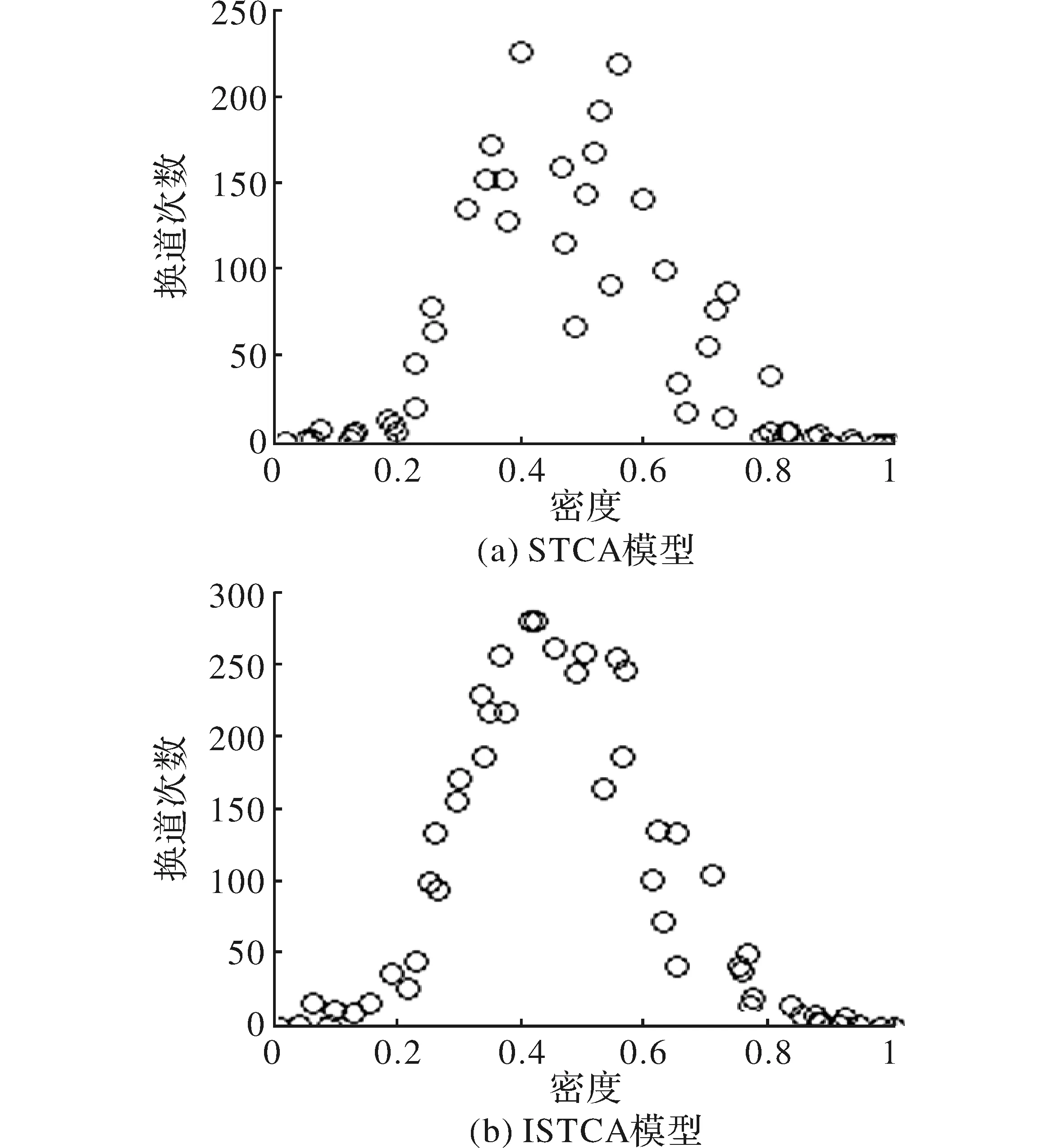
图7 不同密度条件下换道次数

(2)当密度达到一定程度(0.27～0.35)时，随着车辆的增加，车辆行驶自由度受限，换道行为频繁发生，STCA模型从临车间间距状态判断换道行为，而ISTCA模型采用灵活的换道行为，能有效提高驾驶员速度收益。在该范围内，ISTCA模型通行能力大于STCA模型；另外，ISTCA模型换道的灵活性设置保证通行能力的增长速率，与STCA模型相比，能在相对较低的密度下边达到最大通行能力；

(3)随着密度的增大(>0.4)，道路条件逐渐恶化，车辆换道条件受限，换道次数逐渐减小，STCA模型与ISTCA模型流量回到相近的状态。

4 结束语

本文根据实际道路交通数据对驾驶员换道特性进行分析，研究了驾驶员换道条件的选取，考虑驾驶员的激进驾驶行为后基于元胞自动机建立ISTCA模型。模型仿真结果表明，在自由流和拥挤流情况下，STCA和ISTCA两种模型通行能力基本相同；在由自由流向拥挤流过渡区间内，采用动态换道概率后，激进型驾驶员能通过灵活换道行为，得到速度收益，一定程度上提高了道路通行能力，得到的结果更符合实际驾驶行为。

但是，在实际应用中，车辆换道受到临车加速度的影响，尤其是临道后车的加速度。本文中ISTCA模型没有具体研究。如何确定其相应关系使之更符合实际驾驶行为，仍需要进一步研究。

[1] Nagel K, Schreckenberg M. A cellular automaton model for freeway traffic[J]. Journal de Physique I, 1992, 2(12): 2221-2229.

[2] Chowdhury D, Wolf D E, Schreckenberg M. Particle hopping models for two-lane traffic with two kinds of vehicles: Effects of lane-changing rules[J]. Physica A: Statistical Mechanics and its Applications, 1997, 235(3): 417-439.

[3] Takayasu M, Takayasu H. 1/f Noise in a traffic model[J]. Fractals, 1993, 1(4): 860-866.

[4] Benjamin S C, Johnson N F, Hui P M. Cellular automata models of traffic flow along a highway containing a junction[J].[5]Journal of Physics A: Mathematical and General, 1996, 29(12): 3119-3127.

[5] Barlovic R, Santen L, Schadschneider A, et al. Metastable states in cellular automata for traffic flow[J]. The European Physical Journal B-Condensed Matter and Complex Systems, 1998, 5(3): 793-800.

[6] 魏丽英,王志龙,吴荣华. 交叉口进口道换道行为研究及建模[J]. 物理学报, 2014, 63(4): 44501-044501.

[7] Li X G, Jia B, Gao Z Y, et al. A realistic two-lane cellular automata traffic model considering aggressive lane-changing behavior of fast vehicle[J]. Physica A: Statistical Mechanics and its Applications, 2006, 367(2): 479-486.

[8] Wan X, Jin P J, Yang F, et al. Modeling vehicle interactions during merge in congested weaving section of freeway ramp[J]. Transportation Research Record: Journal of the Transportation Research Board, 2014, 2421(1): 82-92.

[9] 郑亮. 多向刺激条件下的驾驶行为建模及其仿真研究[D]. 天津：天津大学, 2013.

[10] 钱勇生,曾俊伟,杜加伟,等.考虑意外事件对交通流影响的元胞自动机交通流模型[J]. 物理学报, 2011, 60(6): 103-112.

[11] 赵康嘉,陈淑燕. 基于元胞自动机的交通事件交通流仿真模型[J]. 公路交通科技,2014, 31(3): 133-138.

[12] Lighthill M, Whitham G. On kinematic waves: II. A theory of traffic flow on long crowded roads[J]. Proceedings of the Royal Society of London:Series A, Mathematical and Physical Sciences,1955,229(1178): 317-345.

[13] 杨小宝.考虑实施过程的车辆换道模型及其应用[J]. 物理学报,2009, 58(2): 836-842.

[14] 王崇伦,李振龙,陈阳舟,等.考虑换道约束空间的车辆换道模型研究[J].公路交通科技, 2012, 29(1):1002-0268.

[15] Duret A,Ahn S,Buisson C. Passing rates to measure relaxation and impact of lane-changing in queue[J]. Computer Aided Engineering and Infrastructure Engineering, 2011, 26(4):285-297.

Aggressive Driving Behavior Lane-changing Model Research Based on Cellular Automata

DING Shenzhen, YANG Xiaofang, WANG Baili

(Department of Transportation Engineering,University of Shanghai for Science and Technology,Shanghai 200093, China)

In order to research the effect of aggressive driving behavior on highway traffic flow , analysis the realistic data from NGSIM I80(Interstate 80). Come up with an aggressive driving behavior model by the analysis of Space Headway, Lane-changes and other parameters from the data. Modeling ISTCAmodel with dynamic lane-changing probability based on single lane model VDR and two lanes model STCA through cellular automata. The driving behavior in different density is analyzed compare with STCA model. As analysis of simulation delays, with a certain amount of density, ISTCA model can improved capacity effectively.

traffic engineering；aggressive driving behavior；cellular automata；lane-changing model；two lane

2016- 04- 26

国家自然科学基金(51308409；51008196)；上海市浦江人才计划(15PJC075)

丁深圳(1992-)，男，硕士研究生。研究方向：交通工程。

10.16180/j.cnki.issn1007-7820.2017.04.012

U491；TP391.9

A

1007-7820(2017)04-048-04