S波段负阻振荡器的设计

陈营营，马 伟

(西安空间无线电技术研究所 神舟学院，陕西 西安 710000)

S波段负阻振荡器的设计

陈营营，马 伟

(西安空间无线电技术研究所 神舟学院，陕西 西安 710000)

振荡器是通信系统中的关键器件，其性能对整个系统有着重要影响。文中介绍了利用负阻原理设计2.425GHz振荡器的方法。根据负阻原理，使用Agilent公司的ADS软件，采用S参数仿真和谐波分析方法，对振器振荡器进行了仿真设计。根据仿真结果加工了振荡器，并用频谱仪对其进行测量和分析。测得相位噪声为-122 dBc/Hz@100 kHz，谐波抑制为23.6 dB，达到了预期目标。

振荡器；负阻；谐波平衡；相位噪声；谐波抑制

振荡器是频率源的关键部件，其性能对整个频率源的性能有着重要影响[1-2]。 随着通信和微波技术的发展，对频率源的性能要求也越来越高。因此，设计性能优良的振荡器必要的。由于振荡器的非线性特性，振荡器的设计难以找到较精确的模型来分析，从而加大了振荡器的设计难度。本文根据负阻原理，利用谐波平衡法设计振荡器，并对振荡器的输出频谱、非线性噪声进行了分析。

1 负阻原理

微波振荡器是通过谐振电路与微波半导体器件的相互作用，将直流功率转换成射频功率的装置。按工作原理可分为反馈式振荡器与负阻式振荡器两大类[3]。负阻振荡器，主要由确定频率的无源正阻谐振电路(耗能部分)和有源负阻电路(供能部分)构成。单端口负阻振荡器的工作原理如图1所示。图中，ZL=RL+XL是负载阻抗(R代表电阻，X代表电抗)。RL对应耗能部分，即RL>0。Zin=Rin+Xin是有源电路的输入阻抗，对应供能部分。

根据基尔霍夫(Kirchhoff)电压定律

(Zin+ZL)I=0

(1)

振荡器在谐振频率点附近存在有限非零电流I，那么有Zin+ZL=0。将此方程的实部和虚部分开，则可以得到振荡条件

Rin+RL=0

(2)

Xin+XL=0

(3)

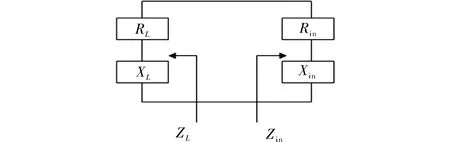
图1 负阻振荡器原理框图

由于RL>0，故RIN<0。考虑到有源器件的非线性特性，根据工程经验，为取得振荡器的最大功率输出，通常取Rin=-3RL，式(3)决定了谐振频率[4]。

2 电路结构

2.1 直流偏置网络

偏置网络用于设置晶体管的静态工作点，静态工作点的选择对振荡器的输出功率和相位噪声有着重要影响[5]。根据0 dBm的输出功率要求以及应尽可能降低相噪，确定直流工作点为IC=18 mA，VCE=4.5 V。

双极晶体管的偏置网络有无源网络和有源网络两大类型。为达到小型化的目的，选用无源偏置网络[6]。根据选定的静态工作点，通过计算并借助ADS软件的优化，最终得到直流偏置网络如图2所示。其中，R1和R2为基极分压电阻，R3为集电极电阻，R4为射极反馈电阻。IC=18.5 mA，VCE=4.6 V。结合工程实际中的标准电阻值，确定4个电阻的阻值分别为R1=3 900 Ω，R2=3 300 Ω，R3=100 Ω，R4=300 Ω。

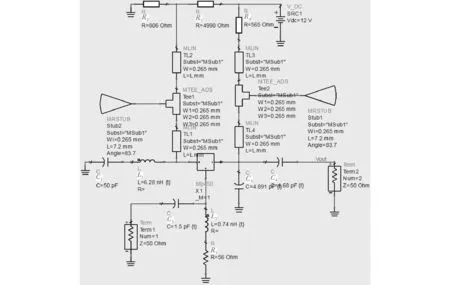
图2 直流偏置网络图

2.2 负阻电路结构

双极晶体管BJT一般采用共基极和共发射极组态[7]，在频率较低处选用共基极组态，当频率达到射频高端时，选用共发射极组态更容易实现稳定的振荡。本文2.425 GHz单频腔体谐振器的设计采用共基极的电路形式，电路结构如图3所示。

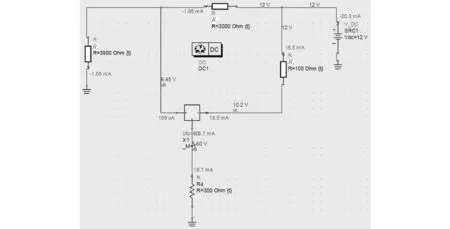
图3 电路整体结构

C1为基极接地电容。射极电容C2为加载电容，谐振器通过C2加载到负阻电路。C2决定了负阻电路和谐振器之间的耦合度。C2越小，耦合度越小，谐振器的负载Q值越高，相噪越好，但是输出功率降低，并且振荡器在某些情况下难以起振。L1为基极正反馈电感，它决定了负阻的形成。射极电感L2作为射频隔离使射极电路呈高阻抗，以保证大部分的能量通过C2被传送到谐振器而不是被R1消耗[8]。集电极电容C5可以将直流通量接地，还具有输出匹配的作用，C4为输出电容。扇形微带线具有隔离射频通路防止射频信号进入直流通路的作用[9]。

3 振荡器的仿真设计3.1 小信号仿真

当电路处于不稳定状态，即K<1时，电路可能产生振荡[10]。可以通过“Stabfact”控件来测量K值。根据实际经验，当mag(S(1,1))>1.2时，电路不稳定。通过调整射频电路中各分立器件的值，使电路满足以上要求。测得Stabfact=-0.863<1，mag(S(1,1))=13.9，说明1端口产生较大能量反射。此时，通过“Zin”控件测得电路的输入输出阻抗

Zin=(-53.508+j6.581)ΩZout=(-48.344-j10.379)Ε

输入输出端均产生较大负阻，但输入输出阻抗的虚部不为零且有较大差距，说明输入输出端口的匹配状况并不好。经过调整C2，C4，C5以及L2，对电路进行优化，得到较理想的结果，如图5所示。

图4 优化后的的参数

由图4可知，在谐振频率附近，稳定性系数为0.144， mag(S(1,1))=686，输入输出阻抗

Zin=(-50.127-j0.072)Ω,Zout=(-50.471-j0.209)Ω

输入输出端都能产生较大负阻且虚部接近为0，说明电路达到了较好的匹配状态。

3.2 大信号仿真

3.2.1 瞬时仿真

瞬时仿真的结果是振荡器的瞬时输出，即在某个时间段的输出波形，从输出波形可以判断出振荡器是否能产生波形以及输出波的振幅。对波形进行傅里叶分析，可以得到这段波形的频谱图，从而得到振荡器的大概的振荡频率[11]。

图5 瞬时仿真输出波形及其频谱分析

在电路中添加“Transient”仿真控件，去掉“Term1”，换成谐振器，去掉“Term2”，在输出端口接50 Ω电阻作为输出负载，对电路进行瞬时仿真。瞬时仿真结果如图5所示。从图5(a)可以看出，振荡器输出波形的上下边缘较为整齐，输出电压较稳定； 通过对m1、m2两点间的波形进行傅里叶分析得到图5(b)，振荡频率约为2.238 GHz。

虽然瞬时仿真可以得到振荡器的输出波形和振荡频率，但是振荡器的相位噪声很难从瞬时仿真中看出。

3.2.2 谐波平衡仿真分析

谐波平衡(Homnic Balance，HB)法是研究非线性电路的非线性特性和系统失真的仿真分析法。在谐波平衡仿真器中，非线性系统用时域描述，线性系统用频域描述，然后将时域和频域通过傅立叶分析结合起来[12]。它将电路状态变量近似写出傅立叶级数展开的形式，通常展开项必须取的足够大，以保证高次谐波对于模拟结果的影响可以忽略不计。

对振荡器而言，采用谐波平衡分析的目的就是进行大信号的非线性模拟。通过它可以模拟振荡器电路的噪声分析，确定谐波成分及谐波功率[13]。经过优化调谐，最终得到仿真结果如图6所示。

由仿真结果可知，基波频率为2.447 GHz，基波输出功率为7.928 dBm，最大谐波输出功率为-13.817 dBm，谐波抑制约为21.7 dBc，达到了设计要求。调频噪声为-154.254 dBc/Hz@10 kHz；相位噪声为-155.425 dBc/Hz@10 kHz。

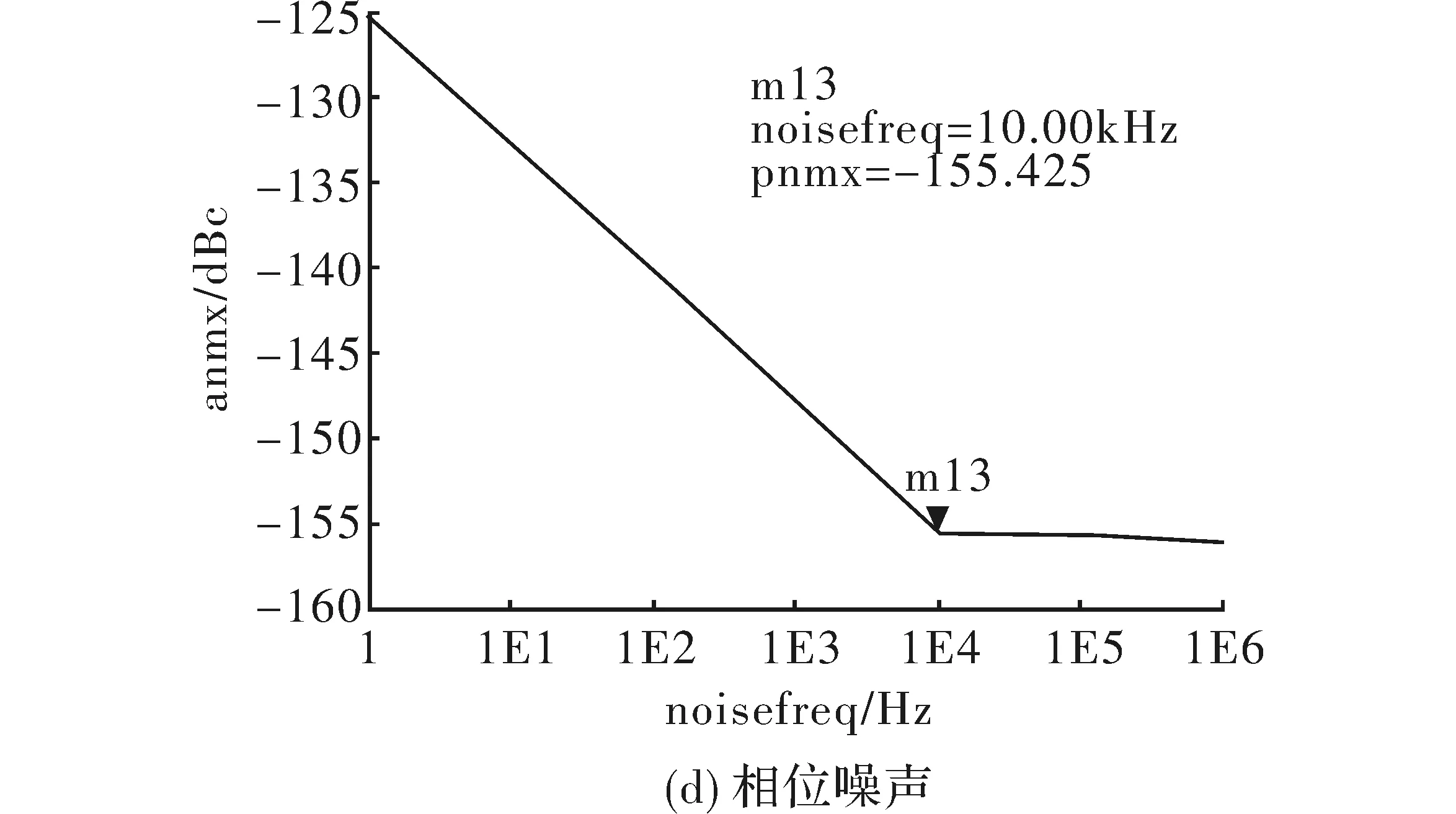
图6 谐波平衡仿真结果

由于电感比电容有更高的电阻性损耗[14]，所以在此类电路中通常避免使用电感。电路对电感值变化较敏感，实际应用中的分立电感值难以满足电路需求，所以本文用微带线代替电感。分立器件之间的联接也用微带线，而微带线具有阻抗变换的作用，微带线的引入必然会改变原输入输出端的阻抗值，所以，在借助计算机仿真设计时要考虑到这一点。

引入微带线的过程，虽然理论上非常简单，但由于多处用到微带线，电路中的变量较多，且考虑到实际加工对微带线加工长度的规定，变量的变化范围应符合要求，加上电路比较敏感，其仿真过程较为复杂。

4 实物加工及测量结果

实物加工采用罗杰斯4350基板，由中国电子科技集团公司第56研究所加工。用Agilent E3649A频谱仪进行相位噪声、谐波频率及输出功率的测量，测量结果如图7和图8所示。

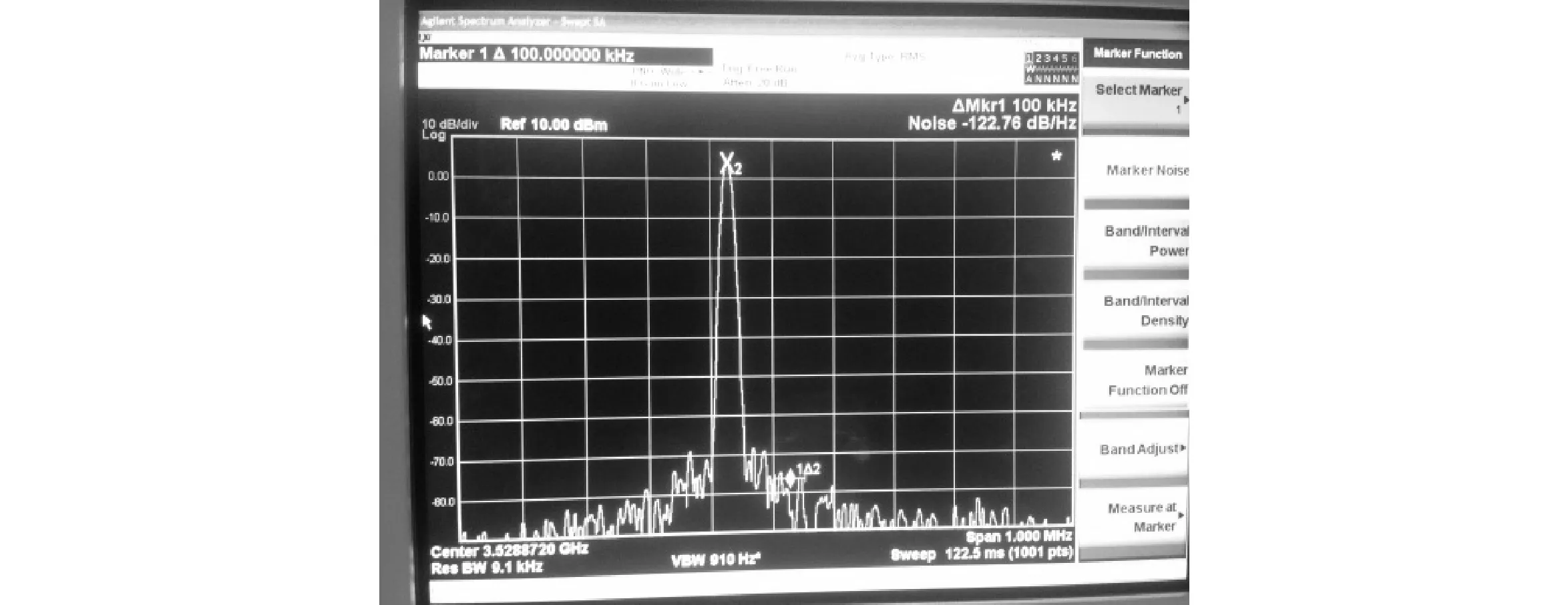
图7 相位噪声的测量

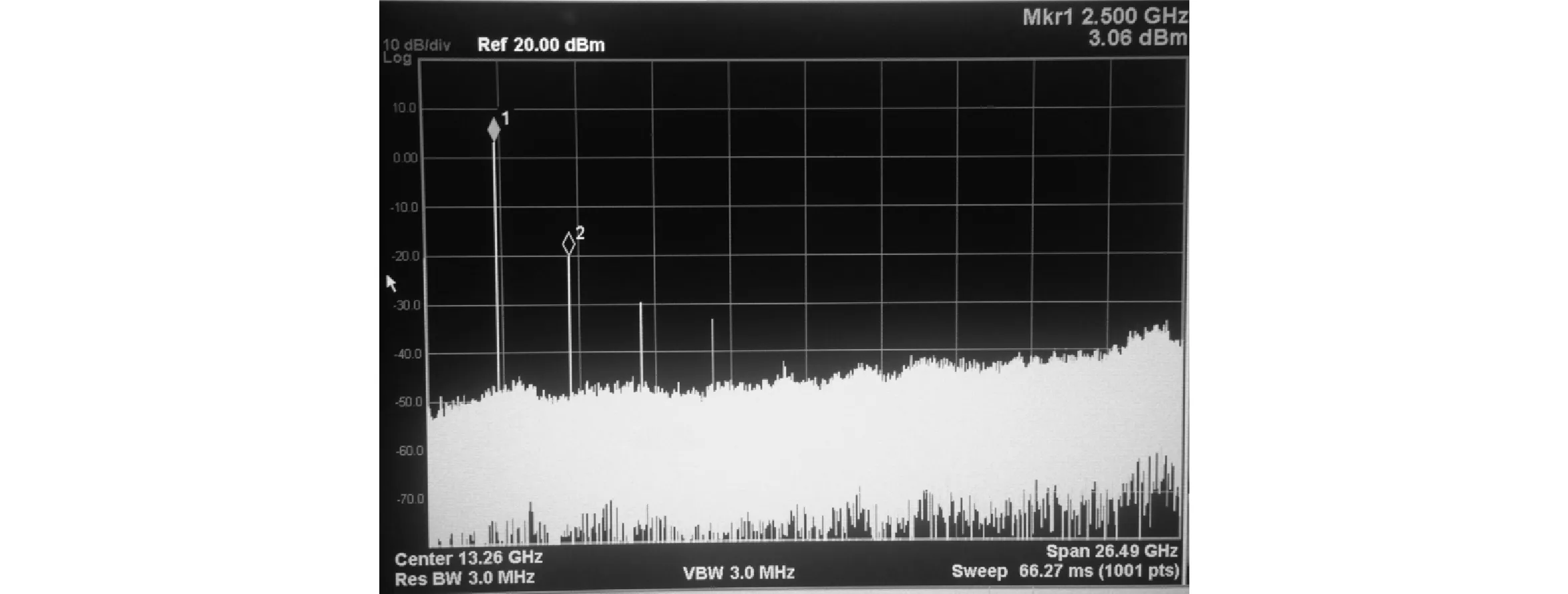
图8 谐波功率的测量

ADS原理图仿真是在完全理想的状态下进行的计算，没有考虑到各种干扰因素和加工精度，实物加工的测量结果与仿真结果有一定的差距。

实测振荡器的中心频率为2.498 GHz，略高于设计要求的频率2.425 GHz，这与谐振器的加工精度有关。所用谐振器的频带特别窄，其谐振频率决定了振荡器的振荡频率。仿真所用谐振器的S2P文件是从厂家官网下载的数据，其中心频率为2.425 GHz，低于实际使用的谐振器频率。

本振荡器没有加锁相环，振荡频率会发生抖动[15]，难以测量偏离中心频率10 kHz处的相位噪声，所以只测量了100 kHz处的相位噪声，测量结果为-122 dBc/Hz@100 kHz。基波功率为3.06 dBm，二次谐波的功率为-20 dBm，谐波抑制达23.6 dB，达到了设计要求。

5 结束语

振荡器是通信系统中的关键器件，其性能对整个系统有着重要的影响。因为振荡器利用了有源器件的非线性特性，其仿真模型的选择尤为重要。振荡器工作时有源器件处于不稳定状态，所以振荡器是非常敏感的。设计出较稳定的电路结构是必要的，在仿真时应考虑到各极之间的电磁干扰，还要将实际加工中引入的寄生参量等效到电路中去，这需要一定的工程积累。

[1] John C,Grebenkemper,和新阳,雷颖蓓.本振相位噪声及其对接收机性能的影响[J].空间电子技术,2009(1):4-13.

[2] 张旭.相位噪声对测控通信系统数传性能的影响[J].空间电子技术,2014(1):55-58.

[3] 王子宇.射频电路设计-理论与应用[M].北京:电子工业出版社,2002.

[4] 唐学锋.低相位噪声宽带LC压控振荡器设计[J].电子技术应用,2015(11):54-57.

[5] 王颖,马伟.8.5GHz双极型晶体管振荡器的设计[J].空间电子技术,2008(4):64-66,97.

[6] 陈君涛.基于SFCR新型介质的X波段压控振荡器的研究[C].西安:全国微波毫米波会议论文集,2009.

[7] 张海挺.4GHz低相噪微波介质振荡器的设计与研究[D].南京:南京邮电大学,2012.

[8] 王红梅,温艳兵,王毅刚.C波段高稳定陶瓷谐振振荡器的设计[J].电子设计工程,2011,22(3):101-103.

[9] 王培培,田立卿,刘德喜.一种L波段陶瓷振荡器的设计[J].遥测遥控,2012(4):46-49.

[10] 蒋泽民,闫述.低相噪4.9GHz微带振荡器[J].无线通信技术,2015(4):55-59.

[11] 李鹏亮,马伟.Ka波段单片压控振荡器的设计[J].现代电子技术,2014(13):77-80.

[12] 崔本亮.负阻元件的设计与应用实验[J].电子世界,2014(16):462-463.

[13] 李彪,潘安,李家强,等.S波段简易压控振荡器的设计与实现[J].现代雷达,2015(4):65-68,72.

[14] 周文骏,张雪峰,陈建新.具有深度二次谐波抑制的低相位噪声射频振荡器[J].南京理工大学学报,2015(4):477-482.

[15] 庄绪德.C波段DRO的设计[J].电子与封装,2015(9):33-35.

Design of S Band Negative Resistance Oscillator

CHEN Yingying , MA Wei

(Shenzhou Collage,CAST-Xi’an Institute of Space Radio Technology,Xi’an 710000,China)

This paper introduced the method of designing a 2.425 GHz oscillator by the principle of negative resistance. Based on the principle, with the help of the ADS software of Agilent company, using theSparameter simulation and harmonic balance analysis method, we designed the oscillator. We processed the oscillator according to the simulation results, moreover, we measured and analyzed it with spectrum analyzer. Phase noise less than -122 dBc/Hz@100 kHz,harmonic suppression more than 23.6 dB.

oscillator;negative resistance;harmonic balance;phase noise;harmonic suppression

2016- 05- 07

陈营营(1989-)，女，硕士研究生。研究方向：空间微波技术。马伟(1960-)，男，研究员，硕士生导师。研究方向：卫星通信及应用系统。

10.16180/j.cnki.issn1007-7820.2017.04.003

TN751

A

1007-7820(2017)04-011-05