初中数学问题解决的双向翻译策略
☉浙江杭州市清泰实验学校 张娟萍
初中数学问题解决的双向翻译策略
☉浙江杭州市清泰实验学校 张娟萍
数学问题解决是数学教与学的重要组成部分.目前,有大量关于解题技巧和题目类型方面的研究.但是还有很多学生虽能听懂老师讲的例题,但自己解决问题时无从下手,或者同种类型的可以解,变换一下条件就不会了;也有学生对公式、定理滚瓜烂熟,就是不知道什么时候用哪一个.学生更需要问题解决策略的通法指导.
其实,数学问题解决的实质就是一个双向翻译的过程.翻译,通俗地讲就是把一种语言文字(源语言)的意义用另一种语言文字(目标语言)表达出来,包括理解、转换、表达三个环节.在这里,源语言就是指数学问题中的语言表述内容,目标语言则指数学语言.双向翻译,包含两个方面:首先是阅读源语言,理解分析其含义,将其信息转换成目标语言;通过数学语言的操作(建模、解模)得到数学结论;然后把数学结论,用一般人所能理解的非数学语言表述出来,从而对实际问题的解决进行解释.后面部分我们称之为“回译”,在回译时数学结论成了源语言,最后表述的非数学语言变成目标语言.数学问题解决的双向翻译,包含以下四个步骤:阅读—翻译—建模、解模—回译.
一、阅读题目的材料——审题过程
翻译必然是以阅读问题为起点的,之所以称为“阅读”,而不是“看”,是指有意识地进行观察,要“领会”材料的意义:把材料叙述的基本内容转化为条件和目标的形式,弄清已知条件是什么、这些条件之间有什么联系、有哪些隐含条件等,这就是审题过程.
1.理解题目信息的含义.
数学语言由文字语言、符号语言和图表语言构成,每一个运算、字符、图表、点等都具有特定的含义和功能,要咬文嚼字地理解数学材料中这些元素所代表的含义.比如,对于-7×3和(-7)×3,粗看这两个式子没有什么区别,只是写法不一样罢了,而当你“咬文嚼字”时,就会发现第二个式子比第一个式子多了一个“()”,进而分析两个式子的深层次涵义,由于括号是整体的意思,也就是说第二个式子的被乘数是(-7),第二个式子应该理解为“负7与3的积”,而第一个式子没有加括号,那么被乘数就是7,而前面的“-”又是怎么回事呢?通过思考进一步就会发现这里的“-”是表示“相反的”,那么第一个式子应该理解为“7与3的积的相反数”.这样,才算真正理解了两个式子的涵义.
一些数学的关键词如“有”“或”“和”“一定不”“不一定”“不多于”“增长了”“增长到”等,对正确理解材料信息起着很关键的作用.
再比如,标点符号“;”,语文中表示“并列”,用“且”“和”“同时”表示,在数学中表示两个条件并列常以“;”为标志.例如,浙教版七下P46课内练习2:甲、乙两人从相距36千米的两地匀速相向而行①.如果甲比乙先走2小时,那么他们在乙出发后经2.5小时相遇②;如果乙比甲先走2小时,那么他们在甲出发后经3小时相遇③.求甲、乙两人每小时各走多少千米.(以下简称“案例”)条件①后面是“.”,表示这个条件是大前提,②与③之间是“;”,表示两个并列的条件,这样应该由②与③得到两个并列的式子,并且都满足①.
另外,数学材料的语言组织常常有省略现象,所以数学阅读不像自然阅读一样流畅,有时需要将省略的字符进行还原或补充.而且,数学知识具有系统性,新的数学材料中常常包含很多下位知识有关的语言,阅读时,要提取出这些下位知识.
2.分析语句表达的结构.
要对句子结构包括句子主干、词与词的关系、句式进行分析.例如,“几个相同因数①的积的运算②,叫作乘方③”这一概念,首先可以分析出句子的主干部分是“积的运算叫作乘方”,“几个相同因数①”是“积”的限定性条件,这样就可以得出“满足因数相同①”这一要素的“积的运算②”才是乘方③运算,这样也有利于理解“积的运算”也就是“乘法运算”与“乘方运算”的关系,得出“乘方运算”是一种特殊的“乘法运算”的深层理解.
还要重视数学表示的特殊句式.数学材料中常见的复合句的句法结构有并列关系和嵌套关系.例如,在“直角三角形①三条边②的垂直平分线③的交点④是斜边的中点⑤”这句话中,“直角三角形①”修饰“三条边②”,二者共同修饰“垂直平分线③”,三者又共同修饰“交点④”,这几个概念构成三重嵌套关系.
数学表达还跟表述顺序有关,如“x与y的平方和”“x与y和的平方”这两个句子,构成的字母都是相同的,但字母的排列顺序不同,使得两个句子的意义完全不同.
3.标注题目条件的信息.
数学实际问题中相互关联的信息常常交错复杂地呈现,阅读时,要善于从大量的信息中,过滤掉干扰信息,提取有效信息.在有效信息下面划线标注,突出条件信息,并且在每个划线条件后面标记序号:一是有利于厘清条件结构;二是方便计条件个数.划线和标注序号后,在下一步操作(翻译)时,只要悉数对照序号①②③代表条件的信息,如果解题碰到挫折要重新回到原题时,只要重新审视这些序号所代表的信息即可,避免重复经历过滤干扰信息等阅读过程.
比如,浙教版七下P46课内练习2中:第一步:阅读题目,划线标出条件信息,并标注序号①②③.“甲、乙两人从相距36千米的两地匀速相向而行①.如果甲比乙先走2小时,那么他们在乙出发后经2.5小时相遇②;如果乙比甲先走2小时,那么他们在甲出发后经3小时相遇③.求甲、乙两人每小时各走多少千米.”
例如,“红红两天看完一本小说①,第一天看了全书的40%②,第二天比第一天多看了15页③,这本书共多少页?”
有学生没有用到“两天看完①”这个条件,导致问题无法解决、实际上很多学生,在识别出“两天看完①”和“第一天看了全书的40%②”时,就自动得出“第二天看了全书的60%”(标注‘②’),完成了数学翻译“引申”的任务.解决问题时,相当于条件是①‘②’③.
在完成全部操作后,仍旧无法解出问题时,要重新审视所有条件,将用到的条件序号划去,看还剩下什么序号标识条件没有运用,如这些条件也没法用上,则要考虑条件的翻译和变式,有时还需要挖掘隐含的条件将省略掉的内容补充完整,增补序号.
二、翻译标注的信息——数学化过程
这里的翻译,是指“双向翻译”的前面部分,就是将阅读时标注的条件信息翻译成数学语言的过程.
1.根据标注信息翻译成数学表述.
(1)积累关键性词语的数学表述.
很多学生采用直译的方式,“直接”按照文字描述的顺序逐字“翻译”,但直译并不一定能实现正确的数学化.比如,对于“m的2倍比n大1”,表示为“2m比n>1”.又如,“两个数互为相反数”,表示为“x=-y”.再比如,“用数学符号表示:负数①的奇数②次方③仍是负数④”,有学生先写出了奇数②的表示“2n+1”,再写出奇数次方③的表示“x2n+1”,然后写出负数①的表示“x<0”,尽管“负数”“奇数”“乘方”这些要素都表现出来了,但最终不能整体表示出来.反过来,解释“|x|=-x”的数学意义为:x的绝对值等于负x;解释“ab=1”的数学意义为:a乘以b等于1.
显然,“逐字翻译”,仅仅是将数学符号语言“读”出来了,并不一定能准确地翻译成数学语言,所以,需要目标语言对翻译的导引.平时要积累一些关键性词语与数学运算之间转译的表述.如:大于或超出(>)、不小于或至少(≥)、正数(>0)、非负数(≥0);再比如“多、少、增加、扩大、节约”等这些词对应着数学符号:+或-;题目中的“几倍、几分之几”常与数学符号×或÷相联系.
(2)引申条件信息的数学意义.
数学材料中的语言往往是抽象的、形式化的,所以,要对条件信息进一步引申.比如,“今年的总消费比去年减少10%”可引申为“今年的总消费是去年的90%”,翻译为:今年的总消费=去年的总消费×90%.
例如,多边形的概念:由线段①围成的封闭图形②叫作多边形.条件①“线段”解读为“不能是曲线”,条件②“封闭图形”解读为“不能有开口的图形”,那么多边形的要素就明确了.
再如,“x的平方与y的差的倒数”,“平方”“差”“倒数”都是名词,但在翻译时,必须将它们译成“运算”,将“平方”翻译成为乘方运算(自乘二次),将“差”翻译成减法,将倒数翻译成“求倒数”.
2.根据条件结构确定表达框架.
面对条件较为复杂的数学问题,根据条件的结构,首先从整体上确定表达的基本结构框架.比如,应用题:G20志愿者人数安排,甲组有40个志愿者,乙组有21个志愿者①,如果要使乙组人数比甲组人数的2倍还多1②,应从甲组调多少人到乙组?解这个题目的关键就在“乙组人数比甲组人数的2倍还多1②”这个条件上,“…的2倍还多1”写成:“2()+1”.所以,将题目的结构表达出来为:乙组人数=2(甲组人数)+1.
又如,“负数①的奇数②次方③仍是负数④”,根据结论“仍是负数④”可以确定题目的框架是“()<0”,再表示()内部即可.
3.根据条件信息确定结构内部.
(1)框架内部内容的表示.如:奇数②表示为“2n-1”(n为自然数);奇数次方③表示为“x2n-1”,再表示x是负数①:“x<0”,最后得出整体表示“若x<0,则x2n-1<0”,”.
再比如,“同号两数相加,取与加数相同的符号,并把绝对值相加.”结合例题(-3)+(-5)=-(3+5)=-8,与法则的每一部分进行同步翻译.第一部分“同号两数相加”,发现(-3)和(-5)同号,都是负数;第二部分,“取与加数相同的正负号”,所以取“-”;第三部分,“并把绝对值相加”,(3+5),其中,3是(-3)的绝对值,5是(-5)的绝对值.
(2)用未知元和已知量表示相关量.比如,上面的问题中,设从甲组调x人到乙组,则甲组人数:40-x;乙组人数:21+x.代入结构框架“乙组人数=2(甲组人数)+1”中,得到21+x=2(40-x)+1.
回到浙教版七下P46课内练习2中,第二步:将这些条件信息翻译成数学语言.设甲、乙每小时分别走x千米、y千米.将①甲、乙两人从相距36千米的两地匀速相向而行,②甲比乙先走2小时,那么他们在乙出发后经2.5小时相遇,翻译成数学语言,即4.5x+2.5y=36;将①甲、乙两人从相距36千米的两地匀速相向而行,③乙比甲先走2小时,那么他们在甲出发后经3小时相遇,翻译成数学语言,即3x+5y=36.
“;”表示“并列”,翻译成数学语言“{”.

翻译的过程,自然进入到第三步:使得该问题与方程组建立联系,问题转换为解方程组.
根据以上例子我们不难发现:数学问题是一句句有数量关联的语句构成的,只要我们善于将一字一句译成式子(方程、不等式、函数式、等式),问题就被简单地数学化了.
三、对照条件的模型——建模过程
上述翻译过程,源语言提供的信息与目标语言库中已有模型进行对照,找到匹配的模型,用数学语言表达出来,就是数学建模.首先,分析条件信息中源语言所对应的基本数学知识点,然后搜索该知识点对应的数学基本模型(假设),通过大脑进行识别和对照,确定模型.比如,水果店以每斤2元的价格购进某种水果若干斤,然后以每斤4元的价格出售①,每天可售出100斤②,经调查发现,这种水果每斤的售价每降低0.1元,每天可以多售出20斤③,水果店决定降价销售.销售这种水果要想每天盈利300元④,水果店需将每斤的售价降低多少元⑤?这是关于单价、数量和利润的问题,脑海中联想到模型:单(用变量表示)×量(用变量表示)=总,这就是这个题目整体表达的结构框架.然后,用未知量和已知量来表示相关的量,将内部条件结构表示出来,设每斤的售价降低x元,由①、⑤得单利润:4-2-x;由③得多售出量:0.1x· 20‘③’,由②、‘③’得到销售量:100+0.1x·20;由④得总利润为300元.于是得到:(4-2-x)×(100+0.1x·20)=300.这就建立了二次方程.
不同语言之所以可以转换,是因为:关于同一个知识点的基本模型,不同语言有相应的表征特征.如一次函数不同语言的表征特征如表1所示.
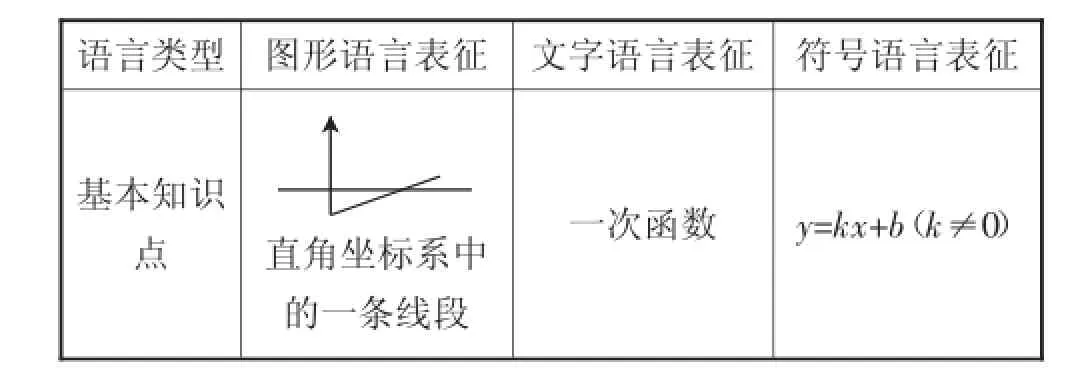
表1
所以,翻译的关键是找到源语言信息中所涉及的基本知识及其对应的基本模型.
文字表述的题目可以直接翻译成示意图.例如:“儿子游学今日回,妈妈早到校门口,儿子到后细端详,母子高兴把家还.”如果用纵轴y表示母亲与儿子行进中离家的距离,用横轴x表示母亲离家的时间,如图1,可以选择第几幅图像表达诗意?
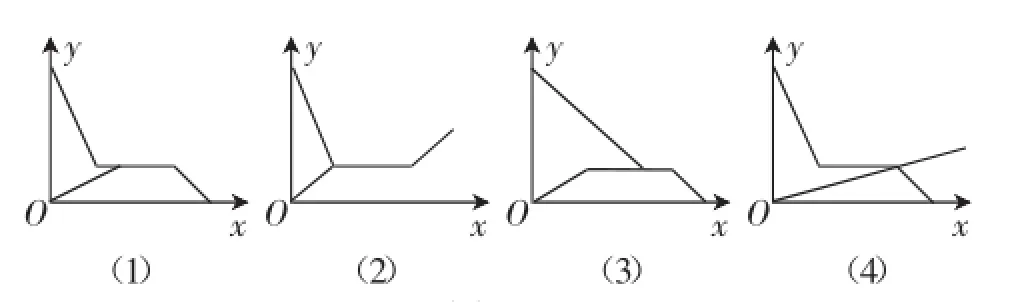
图1
反过来,根据图形,也可以表示相应的实际信息.
例如,根据图2,自编一则新的“龟兔赛跑”故事,并写出龟兔赛跑过程中的函数关系式.这是图像语言、文字语言和符号语言转换的典型例子.

图2
四、回译模型的结论——解释过程
列出模型后,还需解模,就是根据数学知识、技能,解出模型参数的结果.
把参数结果用一般人所能理解的非数学语言表述出来,“从理论分析转回现实语言”,从而对实际问题的解决进行解释.这就是回译,是“双向翻译”的后面部分.
回译首先是检验,将模型解得的参数结果代入实际情形进行比较,如果与实际情景吻合,则可以用这个结果来说明实际问题的结果,从而翻译成实际问题的语言并解释其实际含义.
浙教版七下P46课内练习2中的问题转换为解方程组后,根据方程组的解法规则,解得,从而进入第四步:回译.根据假设“甲、乙每小时分别走x千米、y千米”,把结果翻译成文字语言,即:甲、乙每小时分别走6千米、3.6千米.
如果模型参数的结果与实际情景不吻合,则要重新回到信息的阅读、翻译、建模、解模过程,称之为“迭代”,经过多次反复“迭代”,直至实际问题结果满意为止.
1.张岚.初中生数学学习中自然语言与符号语言的相关性及转化策略[D].陕西师范大学硕士学位论文,2008(5).
2.汤强.7~9年级学生数学符号语言的理解与表示[D].西南大学博士学位论文,2009(5).
3.王丽.预设“问题串”渐次推进新知生成——以“有理数乘法”第1课时教学为例[J].中学数学(下),2016(11).
4.严坤妹.浅谈培养和提高学生数学建模能力的对策[J].福建商业高等专科学校学报,2011(2).

