善用类比推理提升教学实效

陈国仙

摘 要：在小学数学课堂教与学的过程中，教师常感慨要新授的知识量太多，难以完成教学任务，而学生也难以达到学习目标。但在教学过程中，教师常发现很多知识的教学都存在“相似”的感觉，如果教师能将这些“似曾相识”的知识进行系统的梳理，运用类比推理进行教学，则能大大减轻学生学的压力，切实提高教师的教学效率。

关键词：小学数学；教与学；类比推理；方法；效果

一、运用类比推理巧记进率

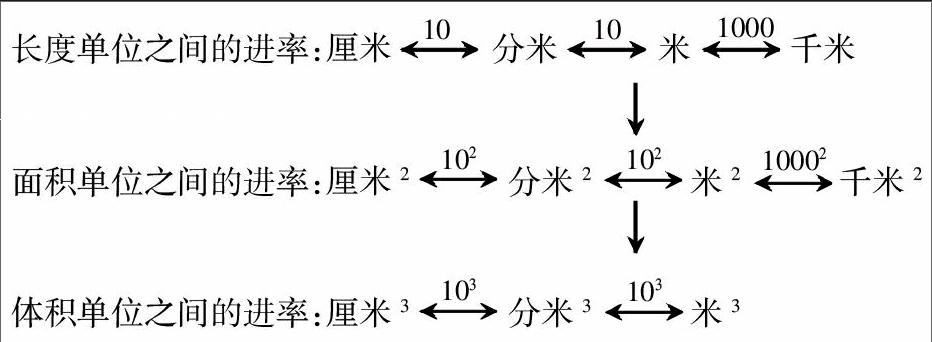
例如，在教学完体积单位间的进率之后，学生对长度单位、面积单位、体积单位的进率常常混淆。学生对相邻长度单位之间的进率是10记得比较牢，学了面积单位后，基本上还可以，但学完体积单位后，学生换算单位之间的进率，常将面积单位之间的进率当作体积单位之间的进率来用，以致出现：2.3米3=（230）分米3这样的错误。于是我在梳理知识时，引导学生从已学的知识进行推理：

发现：由长度单位变成带“平方”的面积单位或带“立方”的体积单位，其进率也跟着变成带“平方”或“立方”。这样，学生只要记住了长度相邻单位之间的进率，就能通过类推而巧妙记住面积或体积相邻单位之间的进率。由此，也就很容易由米与厘米之间的进率为100，而记住米2到厘米2的进率为1002，为学生顺利进行相关单位之间的换算扫清了障碍。

二、运用类比推理巧解方程

在教学解方程时，新教材根据等式的基本性质来解：等式的两边同时加上或减去，乘或除以一个（不为0）的数，达到移项的目的，来求得方程的根；旧教材则根据四则运算算式中各部分间的关系来求解。为提高学生解方程的正确率，在教学这两种题型的方程时，笔者尝试采用化繁为简的方法，引导学生运用类比的思想，将同一种数学方法迁移到不同的数学问题之中，充分发挥类比思维在解题教学中的作用。如，教学8.5÷x=17时，先引导学生举一个10以内的除法等式写在原式相对应的数字上进行类比：

原来解方程可以这么简单！学生顿悟，学生一贯很害怕的解方程得以迎刃而解。教学中要学会常态化利用低年级的知识进行类比，使高年级的数学问题降为中年级，甚至低年级的问题，从而使学生在解题时能做到得心应手。

三、运用类比推理巧学规律

以关于两个事物某些属性相同的判断为前提，推出两个事物的其他属性相同的结论的类比推理，在教学中具有重要的正迁移作用。在小学阶段，学生要相继学习“商不变的规律”“分数的基本性质”和“比的基本性质”。分数的基本性质是在学生学习过商不变规律、分数与除法的关系后进行教学的。在除法里，被除数和除数同时乘或者除以一个相同的数（0除外），商不变。而分数和除式又有千丝万缕的关系，分子相当于被除数，分母相当于除数，除号相当于分数线，这样就可以很容易推出分数的基本性质，进而促使学生的数学思维实现了从感性走向理性的一次飞跃。

四、运用类比推理巧获解法

如，一堆木材，呈梯形堆砌，最上面是4根，最下面是9根，每上一层少一根，共6层，这堆木材共有多少根？多数学生的解法是采用“4+5+……+9=39”来求得木材根数，这种“土”方法学生比较好理解，但是如果数据较大时计算起来就显得繁琐。是否有更简洁的计算方法呢？

有，可以利用等差数列求和的方法：（首项+尾项）×项数÷2，但是要将这么抽象的公式教给学生，肯定得花不少时间与精力。这时我引导学生观察这堆木材的横截面像什么——梯形，那么是否其根数计算方法与梯形的相关公式有关系呢？这样，让学生通过类推与验证，导出可套用梯形的面積公式：

梯形的面积=（上底+下底）×高÷2

木材根数=（上底根数+下底根数）×层数÷2=（4+9）×6÷2=39（根）

此时，我再继续深化教学：“有一堆木材，呈三角形堆砌，最上面是1根，最下面是7根，每上一层少一根，共7层，这堆木材共有多少根？”有了上面知识的积累与铺垫，学生很容易理解这堆木材虽呈“三角形”堆砌，实则是“上底为1、下底为7、高为7的梯形”，解法自然水到渠成：（1+7）×7÷2=28（根）。

类比推理在小学数学教学中发挥着重要作用，通过强化对学生类比推理能力的培养，也定会让课堂绽放异彩。

参考文献：

[1]金李会.类比法在小学数学教学中的运用[J].新课程研究（基础教育），2011（3）：35-36.

[2]黎光兰.试论小学数学教学中的类比推理[J].科海故事博览（科教创新），2013（3）：17-18.

编辑 王团兰