基于迭代算法的水泥水化动力学多元方法研究

胡 超, 刘东泽, 韩 丁, 逄焕平

(1.合肥工业大学 汽车与交通工程学院,安徽 合肥 230009; 2.中铁城市规划院有限公司,安徽 芜湖 241000)

基于迭代算法的水泥水化动力学多元方法研究

胡 超1, 刘东泽2, 韩 丁1, 逄焕平1

(1.合肥工业大学 汽车与交通工程学院,安徽 合肥 230009; 2.中铁城市规划院有限公司,安徽 芜湖 241000)

为合理确定水化动力学分析的参数和实现研究手段多样化,文章提出一种参数识别迭代算法,并探讨了获取水化热数据的数值试验和替代水化热法的背散射电子(back-scattered electron，BSE)图像识别。针对Krstulovic水化动力学模型,通过迭代算法得出各水化阶段的控制时间,为参数识别提供有效的数据区间;使用COMSOL软件建立与绝热温升试验工况一致的数值仿真试验,并将获得的水化温度曲线和最大水化放热量与试验数据进行了比较;识别不同水化时期水泥浆体BSE图像中水化产物的面积比,作为水化程度来确定水泥水化指数函数方程,并与试验数据对比来评价该方程的预估精度。依据迭代算法获取了合理的水化动力学参数,其生成的水化速率曲线与试验数据具有较好的吻合度;水泥水化数值仿真试验可以用来预测绝热情况下水泥混凝土的温度变化,能替代绝热温升试验;依据BSE图像中水化产物面积比获得的水化指数函数与试验数据的吻合度较好,能替代传统水化热法进行水化动力学分析。

水化动力学;水化方程参数;迭代算法;数值仿真;背散射图像识别

水泥基材料是重要的工程建筑材料,由于其组分的多样性和水化活性不同,导致水化反应机理的研究变得极其复杂。水化动力学从动态角度研究了水泥水化的整个过程,并能够得到水化程度及水化速率等参数的变化情况,可用来量化描述水泥水化的特征。基于水化产物同心层统一均衡生长理论,文献[1]使用单球形水泥颗粒描述单一组分C3S的水化动力学；文献[2]进一步提出水泥水化反应的动力学模型,并把水化反应分成结晶成核与晶体生长(NG)、相边界反应(I)和扩散反应(D)3个基本阶段；文献[3-4]提出一种识别Krstulovic动力学模型各阶段[2]的方法,发现当胶凝材料处于NG或I阶段时,混凝土强度随之明显增长,当水化反应进入D阶段时,混凝土强度增长幅度减小。

温度会影响水泥的水化过程。文献[5]利用ABAQUS软件模拟了混凝土结构的温度场分布,并利用绝热温升曲线确定了混凝土等效龄期水化度曲线,最终得到温度和龄期对水泥水化放热过程的双重影响。

图像分析法能区分不同成分区域,文献[6]采用图像分析法得到水泥浆的泛霜面积,进而评价试件表面泛霜程度。背散射电子(back-scattered electron，BSE)图像法能描述水泥基材料特性,已成功应用于水泥水化研究。为研究水泥水化时微观特征的变化,文献[7]利用BSE图像分析得到了不同水化程度时水泥浆体各组分特征的变化。

目前Krstulovic水化方程的参数识别缺少各阶段作用时间的划分依据,需要的试验数据多采用等温量热法获取,而BSE法还未能直接用于水化动力学研究。本文使用一种新的识别算法来合理划分Krstulovic水化方程各基本阶段的控制时间,探讨了采用水化热仿真试验替代真实等温量热试验的可行性,并研究了直接采用水泥浆体BSE图像进行水化动力学分析的方法。

1 识别水化动力学参数的算法

利用水化程度试验数据能获取水化动力学模型的参数,本文提出一种获取Krstulovic水化动力学模型各阶段控制时间的迭代方法,可为参数识别提供有效的数据区间。

1.1 水化动力学模型

Krstulovic水化动力学模型将水泥基材料的水化反应划分为3个基本方程,动力学方程分别见(1)～(3)式。水化反应一般采用NG—I—D或NG—D 2种不同的历程,在不同的水化阶段分别由反应最慢的水化动力学方程控制。

在结晶成核与晶体生长(NG)阶段,有

(1)

在相边界反应(I)阶段,有

(2)

在扩散反应(D)阶段,有

(3)

其中,kNG、kI、kD分别为3个阶段的反应速率常数;n为反应级数,代表几何晶体生长,取值范围为1～3。

水化速率是水泥水化的主要特征之一,分别将(1)～(3)式对时间求导,可得到水化速率微分方程组[3]如下：

(4)

(5)

(6)

1.2 参数识别迭代算法

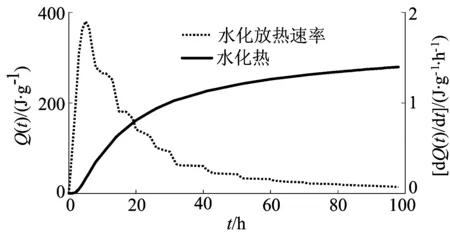
(1) 第1次迭代时,假定NG和I阶段的结束时间分别为t1和t2,t1

(2) 分别将t1之前和t1与t2之间的水化程度数据作为NG和I阶段的有效数据区间,通过(1)式和(2)式识别参数n、kNG和kI,进而得到NG和I阶段控制下的水化程度曲线αNG(t)和αI(t)。

(3) 对比曲线αNG(t)和试验数据曲线α(t),得到2条曲线的分叉点,将其对应的水化时间作为NG阶段控制的初定结束时间t1a。

(4) 对比曲线αI(t)与α(t),如果两者在t1a之后吻合程度较差,说明I阶段不存在,直接利用t1之后的数据得到kD;如果两者在t1a之后存在吻合段,说明I阶段存在,将曲线αI(t)和α(t)的分离点所对应的水化时间作为I阶段的初定结束时间t2a。利用(3)式由t2之后的试验数据得到kD。

(5) 若I阶段不存在,则将参数n、kNG和kD分别代入(4)式和(6)式中,按反应最慢的过程控制水化反应的原则,得到NG阶段结束时间t1b。若比较t1a和t1b,两者误差较小或者继续迭代对t1b没有影响,则认为该次迭代得到的t1b为NG阶段的结束时间,n、kNG和kD即为最终的动力学参数;否则利用t1b替代t1,按照步骤(1)～步骤(4)重新进行下一次迭代。

(6) 若I阶段存在,则将参数n、kNG、kI和kD分别代入(4)～(6)式中,同理得到NG和I阶段的结束时间t1b和t2b。若t1a和t1b、t2a和t2b间的误差均较小或者继续迭代对t1a和t1b没有影响,则认为该次迭代得到t1b和t2b分别为NG和I阶段的结束时间,n、kNG、kI和kD即为最终的动力学参数;否则利用t1b和t2b分别替代t1和t2,按照步骤(1)～(4)重新进行下一次迭代。

(7) 将最终得到的动力学参数分别代入(4)～(6)式中得到Krstulovic模型预测的水化速率,与水泥水化速率试验数据进行对比验证参数的合理性。

2 基于水化热法的水化动力学

水化热法是研究水化程度的常用试验,本文使用水化热试验数据验证迭代算法的合理性,并对使用数值仿真替代常规水化热试验的可行性进行探讨。

2.1 基于迭代算法的参数识别

根据水泥基材料的水化放热量Q(t),由(7)式和(8)式[3]可求得最大放热量Qmax和水化程度α(t)。采用文献[3]中某硅酸盐水泥(简称CEM I)水化热热量的试验数据,识别得到(7)式中的3个参数分别为:

Qmax=338.5 J/g,t0=2.439 h，t50=22.09 h。

最大放热量的识别曲线如图1所示。

图1 最大放热量的识别曲线

得到最大放热量Qmax后,根据(8)式可得到水化程度,水化程度-时间曲线如图2所示。

图2 水化程度-时间曲线

(7)

(8)

其中,α(t)、Q(t)分别为t时刻的水化程度和水化放热量;t50为放热量达到Qmax的1/2时所需要的时间;t0为诱导期结束时间。

对(1)式两边同时取对数得到：

(9)

假定初始时t1=10、t2=20 h,采用图2中前10 h的α-t数据获得参数n=1.635、kNG=0.043 3,NG阶段参数的拟合结果如图3所示。将该参数代入(1)式得到NG阶段的水化程度曲线αNG(t),与α(t)进行对比,如图4所示,得到2条曲线的分离点所对应的时间t1a=14.8 h。

图3 NG阶段参数拟合图

图4 NG、I阶段水化程度与试验数据的对比

采用图2中t1与t2之间的α-t数据获得参数kI=0.012 1,将kI代入(2)式得到I阶段的水化程度曲线αI(t),与图2中试验数据曲线α(t)进行对比,两者存在吻合曲线段,见图4,说明I阶段存在,且曲线αI(t)与水化程度曲线α(t)的分离点所对应的时间t2a为21.5 h。采用图2中t2后面的α-t数据获得kD=0.002 5。

将参数n、kNG、kI和kD分别代入(4)～(6)式可得到水化速率预测曲线,如图5所示。NG与I和I与D水化阶段曲线交点对应的水化程度分别为0.12和0.33,在图2中其相应的时间t1b和t2b分别为6.5 h和12.5 h,与t1a和t2a相差较大,因此需要进行下一次迭代,并将t1和t2分别替换为6.5 h和12.5 h。文中共进行4次迭代,结果见表1所列,由第4次迭代结果发现t1b和t2b趋于稳定,因此将此次迭代得到的计算结果作为CEM I水泥的各动力学参数值。

图5 3个阶段的预测水化速率

迭代次数t1at1bt2at2bnkNGkIkD114 86 521 512 81 6350 04330 01210 0025212 97 817 712 01 6990 04600 01190 0028311 77 916 911 61 7340 04710 01180 0026411 77 916 311 51 7340 04710 01170 0026

将(8)式对时间求导得到(10)式,该式表明水化速率与水化放热速率呈线性关系。将CEM I水泥的水化放热速率数据dQ(t)/dt代入(10)式[3]转化为水化速率试验数据dα(t)/dt,如图6所示。

(10)

将识别的CEM I水泥各动力学参数值分别代入(4)～(6)式,按照反应最慢的过程控制水化反应的原则,将各阶段水化方程曲线交点对应的时间作为控制方程发生转变的分界点,得到使用识别参数的Krstulovic动力学模型对水化速率的计算结果,如图6中模拟速率曲线所示。比较模拟速率曲线和水化速率试验数据曲线,两者吻合较好,表明本文提出的参数识别算法具有合理性。

图6 Krstulovic模型模拟的水化速率与试验数据的对比

2.2 水泥水化热数值仿真

2.2.1 模型及参数设置

文献[8]中混凝土绝热温升试验是在绝热条件下,测定混凝土胶凝材料在水化过程中的温度变化值。依照试验工况,本文利用有限元软件建立1个φ6×12 cm的圆柱形水泥混凝土试件模型。模型四周设置为绝热条件,模型内部设置为均匀热源。

水泥混凝土组成见表2所列,其比热容值为文献[9]中建议值920 J/(kg·℃-1),水泥的各参数值见表3所列[10],将各参数值和(11)式与(12)式一起输入COMSOL软件中进行仿真计算。根据硅酸盐水泥的组分,单位质量水泥水化放热速率随时间的变化关系[10]可描述为：

(11)

其中,Hu为最大水化放热量;Cc为胶凝材料的容重;Tr为参考温度;Tc为水泥浆体温度;E为活化能,反映水泥水化的温度敏感性;R为通用气体常数;τ为水化时间参数;α(te)为龄期te时刻的水化程度,计算方法[11]为：

(12)

其中,β为水化形状参数;αu为最终水化程度;r为水灰比。

表2 水泥混凝土的组成

表3 TYPE I水泥的各项热力学参数

2.2.2 模拟结果验证

绝热情况下水泥水化的温度试验数据[9]和COMSOL水化热模型的仿真结果对比如图7所示,可以看出两者基本一致,因此水化数值仿真试验可以替代文献[8]中的水泥混凝土绝热试验用来预测绝热情况下水泥混凝土的温度变化。

图7 模拟与试验温度对比

文献[8]中水化放热量的计算公式为:

(13)

其中,Qn为n天龄期水泥水化热;θn为n天绝热温升;CK为混凝土质量与混凝土比热的乘积;W为混凝土试件的水泥用量。

由图7中模拟温度曲线得到水化100 h(即n=4.17 d)对应的θ4.17=42 ℃,随着水化进行,最大温升θmax可达到45 ℃左右。假定水泥混凝土的体积为V,由水泥混凝土比热容值和表2中的数据,可得:

CK=(341+1 104+756+126.2)920V=

2 141 024V,W=341V。

再由(13)式计算得到最大放热量Qmax约为300 J/g。

表3给出了TYPE I水泥完全水化最大放热量Hu为477 J/g,依据试验工况按(12)式得出最终水化程度αu为0.676,因此实际最大水化放热量应为Huαu=322.5 J/g,与通过数值仿真获取的

Qmax较为接近,表明数值仿真得到的放热量曲线具有合理性。数值仿真得出的水化放热速率与放热量曲线如图8所示。

图8 数值仿真得出的水化放热速率与放热量

水泥水化热模型的绝热温升仿真结果能转化为图8中的水化放热量和水化放热速率曲线,可替代水化热法测得的试验数据进行水化动力学分析。

3 基于图像处理的水化动力学

目前水化动力学分析多采用水化热法的试验数据,而BSE图像常用于定量统计物相体积分数[12],本文对BSE图像用于水泥水化动力学分析的可行性进行研究,方法是使用不同水化时期水泥浆体BSE图像中水化产物的面积比来代替水化热数据。

3.1 水泥水化BSE图像处理

BSE图像中物相的灰度与其背散射系数η有关,η越大则此物相在图像中较亮,BSE图像中从暗到亮依次为孔及裂缝、水化硅酸钙(C-S-H)凝胶、氢氧化钙及未水化水泥熟料[12]。文献[13]中某硅酸盐水泥(简称CEM II)在水化4、8、16 h时的BSE图像如图9所示。计算水化产物像素点个数和图像总像素点个数的比值,作为水化产物的面积比。

图9 CEM II水泥不同水化时期的BSE图像

将图像中各物相按亮度分为裂缝及孔、水化产物和未水化水泥熟料3个部分,并分别处理为黑色、灰色和白色,2个灰度阀值分别取为65和160,阀值选取的原则是使得处理后的图像与原始图像保持各组分形状轮廓的一致性。图9中的3张图像处理结果如图10所示,其总像素点个数、水化产物像素点个数和水化产物面积比等结果见表4所列。

图10 CEM II水泥水化BSE图像的数值化处理图

项 目图10a图10b图10c水化时间/h4816尺寸375×374373×371374×369总像素点数140250138383138004水化产物像素点数405724457649884水化产物面积比0 28930 32210 3615

3.2 基于面积比的水化动力学参数识别

水化程度随时间的变化情况可用指数函数较好地描述[11],将表4中的面积比作为水化程度,确定水泥水化的指数函数为α=0.75exp(-8/t)。将该函数曲线与文献[13]中其他时刻(1、7、28 d)的水化程度数据进行比较,结果如图11所示,可见通过BSE图像识别法得到的水泥水化曲线可用来预估水化程度。因此,以BSE图像的水化产物面积比代替传统的水化热法进行水化动力学分析具有可行性。采用上述水泥水化指数函数曲线,依据参数识别迭代算法得到CEM II水泥的各动力学参数,见表5所列。

图11 由数值处理结果拟合的水化程度曲线

参数nkNGkIkD数值1 7560 05490 00890 0014

4 结 论

(1) 本文提出的参数识别迭代算法能较好地划分Krstulovic水化动力学模型各阶段的作用时间,可用来选择各水化阶段的合理数据区间,使用识别参数值得到的模拟水化速率曲线与水化速率的试验数据能较好地吻合,表明该迭代算法具有合理性。

(2) 水泥水化热数值仿真试验能替代绝热温升试验,用来预测绝热情况下水泥混凝土的温度变化,并能转化为水化动力学分析所需的水化热和水化速率数据。

(3) 将水泥浆体BSE图像按亮度分为裂缝及孔、水化产物和未水化水泥熟料3个部分,通过识别不同水化时期水泥浆体BSE图像中水化产物的面积比,并近似作为水化程度,进而得到水化程度指数函数曲线,可代替水化热法进行水化动力学分析。

[1] KONDO R，UEDA S.Kinetics and mechanisms of the hydration of cements [C]//Proceedings of the Fifth International Congress on the Chemistry of Cement.Tokyo：[s.n.]，1968：203-255.

[2] KRSTULOVIC′ R，DABIC′ P.A conceptual model of the cement hydration process [J].Cement and Concrete Research，2000，30(5)：693-698.

[3] 阎培渝,郑峰.水泥基材料的水化动力学模型[J].硅酸盐学报，2006，34(5)：555-559.

[4] 阎培渝,崔强.养护制度对高强混凝土强度发展规律的影响[J].硅酸盐学报，2015，43(2)：133-137.

[5] 钱宏亮，覃锋，范峰，等.台山核电站反应堆筏基混凝土考虑施工过程的温度场模拟分析[J].建筑结构学报，2014，35(8)：134-141.

[6] 贺素仁，詹炳根，周安，等.粉煤灰对硬化水泥浆泛霜的抑制作用[J].合肥工业大学学报(自然科学版)，2012，35(1)：99-102.

[7] GAO Y,DE SCHUTTER G，YE G.A microscopic study on ternary blended cement based composites [J].Construction and Building Materials，2013，46(8)：28-38.

[8] 南京水利科学研究院，中国水利水电科学研究院.水工混凝土试验规程：DL/T 5150—2001 [S].北京：中国电力出版社，2002：66-68.

[9] MORLEY P D，ROYLES R.Response of the bond in reinforced concrete to high temperatures [J].Magazine of Concrete Research，1983，35(123)：67-74.

[10] SCHINDLER A K，FOLLIARD K J.Heat of hydration models for cementitious materials [J].ACI Materials Journal，2005，102(1):24-33.

[11] PANE I，HANSEN W.Concrete hydration and mechanical properties under nonisothermal conditions [J].ACI Materials Journal，2002，99(6)：534-422.

[12] 王培铭，丰曙霞，刘贤萍.背散射电子图像分析在水泥基材料微观结构研究中的应用[J].硅酸盐学报，2011，39(10)：1659-1665.

[13] GALLUCCI E，SCRIVENER K.Crystallisation of calcium hydroxide in early age model and ordinary cementitious systems [J].Cement and Concrete Research，2007，37(4)：492-501.

(责任编辑 张淑艳)

Multivariate methods for hydration kinetics research of cement using iterative algorithm

HU Chao1, LIU Dongze2, HAN Ding1, PANG Huanping1

(1.School of Automobile and Traffic Engineering， Hefei University of Technology， Hefei 230009， China; 2.China Railway Urban Planning and Design Institute Co., Ltd.， Wuhu 241000， China)

In order to determine accurate hydration kinetic parameters and diversify research methods of hydration kinetics， an iterative algorithm was put forward. A numerical model for getting hydration heat and back-scattered electron(BSE) image recognitions for replacing hydration heat method were studied individually. Dominant periods at different hydration processes of Krstulovic kinetic model， which were given by the iterative algorithm， can provide effective data ranges for parameters identifications. A numerical model， which applied the same working conditions of standard adiabatic calorimeter test， was established by COMSOL software. The hydration temperature curve and maximum hydration heat calculated by results of the model were compared with experimental data respectively. Area ratios of hydration products in BSE images at different hydration time were considered as hydration degrees to get an exponential function of cement hydration， whose precision was verified by test data. Reasonable hydration kinetic parameters were obtained by the iterative algorithm. Hydration rate curve， which was created by kinetic parameters， coincides with experimental data. The numerical model of cement hydration can predict temperature variation of cement concrete under adiabatic condition and replace the standard adiabatic calorimeter test. The exponential function of cement hydration， which was obtained by area ratios of hydration products， fits well with experimental data and can be used to analyze hydration kinetics instead of conventional hydration heat method.

hydration kinetics; hydration equation parameter; iterative algorithm; numerical simulation; back-scattered electron(BSE) image recognition

2015-11-05；

2016-12-26

国家自然科学基金资助项目(51008109;51408173);安徽省住房城乡建设科学技术计划资助项目(2013YF-01)

胡 超(1993-),男，安徽颍上人,合肥工业大学硕士生; 韩 丁(1982-),男，安徽肥东人,博士,合肥工业大学副教授,硕士生导师.

10.3969/j.issn.1003-5060.2017.03.019

TQ172.11

A

1003-5060(2017)03-0390-07