基于切比雪夫有理逼近和矩阵自适应降阶的活化计算方法

张彬航，郝丽娟，葛 鹏，宋 婧，何 鹏

(1.中国科学院核能安全技术研究所，中国科学院中子输运理论与辐射安全重点实验室，安徽 合肥 230031；2.中国科学技术大学，安徽 合肥 230027)

基于切比雪夫有理逼近和矩阵自适应降阶的活化计算方法

张彬航1，2，郝丽娟1，葛 鹏1，宋 婧1，何 鹏1

(1.中国科学院核能安全技术研究所，中国科学院中子输运理论与辐射安全重点实验室，安徽 合肥 230031；2.中国科学技术大学，安徽 合肥 230027)

在核反应堆运行过程中，产生的大量中子对结构材料、回路中的腐蚀产物有很强的活化作用，从而对工作人员在运行、检修、退役等多个环节造成辐射危害。因此高精度、高效率的活化计算在反应堆设计和安全分析研究中有着重要的作用。切比雪夫有理逼近方法(Chebyshev rational approximation method，CRAM) 相比于传统的活化计算方法，不需要单独处理短寿命核素，具有计算速度快、精度高、步长包容性好的优点。本文基于超级蒙卡核模拟软件系统SuperMC，采用切比雪夫有理逼近方法，并发展了基于深度优先搜索的活化链动态构建方法和大规模矩阵自适应降阶方法，进行了活化计算的初步研究。通过选用IAEA-ACB(International Atomic Energy Agency-Activation Calculation Benchmark)国际基准例题及压水堆燃料包壳材料例题，初步验证了该活化计算方法的正确性，且测试结果表明，本文发展的大规模矩阵自适应降阶方法能够有效的提高活化系数矩阵的求解效率。

活化计算；切比雪夫有理逼近方法；SuperMC；活化链

反应堆在运行过程中，堆芯内部产生的大量中子会对结构部件、回路中的腐蚀产物有很强的活化作用，所形成的放射性活化产物是反应堆运行及检修人员职业照射的主要来源。因此，精确计算活化问题对于反应堆的安全分析、辐射防护和退役方案的制订具有重要意义。

活化计算主要关心的是材料内的轻核素和中等质量核素受中子辐照后引起的放射性情况。在实际活化计算中，通常涉及的核素种类及反应类型繁多，核素间的转换关系复杂，同时会产生大量的短寿命核素，给活化计算带来困难。目前活化计算方法大致分为解析方法和数值计算方法两类[1,2]。解析方法是将复杂的核素系统转换为一系列的线性子链进行求解，计算速度慢，同时需要引入截断误差。数值计算方法主要包含常微分方程差分解法和矩阵指数法。常微分方程组差分解法对时间步长包容性差，矩阵指数法需要对短寿命核素进行特殊处理，影响计算精度。近年来发展的切比雪夫有理逼近方法(Chebyshev rational approxima-tion method，CRAM)[3]，作为一种新的矩阵指数法，具有计算速度快，精度高、步长包容性好等特点，且不需要单独处理短寿命核素。

本文基于超级蒙卡核模拟软件系统SuperMC(Super Monte Carlo Simulation Program for Nuclear and Radiation Process)[4-6]，采用切比雪夫有理逼近方法，进行了活化计算的研究。SuperMC是FDS团队自主研发的通用、智能、精准的核系统设计与安全评价软件，可用于反应堆的设计与分析[7-11]，辐照屏蔽分析[12-16]等领域。SuperMC目前已通过2000多个国际基准模型与实验的校验[17-20]。

1 活化方程与CRAM方法

(1)

式中，φ(t)表示t时刻的中子通量密度，λi表示核素i的衰变常数，σi,k表示核素i生成核素k单群截面，bj,i表示核素j生成核素i的分支比，yi,j,k表示核素j发生k反应生成核素i的产额。从而问题简化为关于单一变量t的一阶线性微分方程，描述了核反应系统中核素随时间的变化规律。

若定义矩阵元：

(2)

则可将一阶线性微分方程组转换为矩阵形式并得到其指数解的形式如下：

(3)

n(t)=eAtn(0)

(4)

式中，n(t)表示t时刻所有核素密度组成的向量，n(0)表示t=0时刻的初始值，A为系数矩阵。

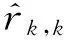
(5)

(6)

式中，I为单位矩阵，k为展开阶数，通过求解线性方程组(6)得到t时刻核核子密度。

2 活化计算中的关键问题研究

在活化计算中，首先建立活化计算的物理模型，包括活化计算涉及的核素、活化反应链及反应率等；其次，采用切比雪夫有理逼近方法对物理模型进行数值求解；最后，根据数值求解得到的核子密度进行活化物理量的计算，包括：活度、余热、接触剂量、衰变光子谱等。本文针对活化计算中活化链构建方式、求解效率等关键问题开展了研究。

2.1 基于深度优先搜索的活化链动态构建方法

在建立活化计算的物理模型时，由于初始材料核素信息通常不包括活化产物的核素信息，因此需要充分考虑材料中核素在中子辐照过程中产生的新核素。FISPACT[21]、ORIGEN等计算程序中采取预先定义的中子活化链进行活化产物添加，但往往覆盖的核素不够全面，扩展性较差。

由于活化涉及的核素种类繁多且变化复杂，需要寻求一种既能覆盖所有核素反应路径又能根据实际问题自动搜索活化产物的算法。本文基于深度优先搜索算法，发展了活化链动态构建方法。从核素的中子反应信息和衰变信息出发，基于深度优先搜索算法跟踪初始核素及其子核的所有反应路径，获得当前问题的解空间，同时在搜索过程中引入截断条件(反应截面、重复核素等)来避免无效搜索，提高搜索效率。当约束条件判断当前反应链终止时，则搜索返回上级子核素开始下一条反应链的搜索，因此在搜索过程就形成了树状结构，如图1所示，从而完成系统内所有核素的添加和活化反应链的动态构建。该方法能够根据初始计算条件自动搜索活化产物并构建活化链，具有扩展性强、精度高的特点。

图1 活化链动态构建示意图Fig.1 Schematic diagram of dynamic construction of activation chain

2.2 大规模矩阵自适应降阶方法

在利用切比雪夫有理逼近方法对活化方程进行数值求解时，大量的短寿命核素会导致系数矩阵规模大，刚性强，直接影响数值求解的效率和精度。考虑到实际的辐照中子能谱，活化链中的部分活化反应可能不会发生，从而对应的活化产物产额为零。这些产额为零的核素会增加系数矩阵的规模，使得求解效率和精度降低。本文发展了大规模矩阵自适应降阶方法，有效降低了系数矩阵的规模和刚性，提高活化计算的求解效率。

在活化计算中，系数矩阵A如图2所示，对角线矩阵元代表核素的总反应消失率，同时对于A中的任意一行，除去对角线矩阵元以外，其余矩阵元分别代表其他行核素生成该核素的反应率。在确定系统内核素与各矩阵元对应关系的条件下，本方法依次对A中的每一个核素的总反应产生率进行判断，若该核素的总产生率为零，则认为该核素对于系统中其他核素的生成没有贡献。同时对该核素进行标记，并将该核素对其他核素的产生反应率置为零。若标记核素的总个数为n，则由该方法处理后得到的系数矩阵规模由原先的m阶降低为(m-n)阶，从而降低了矩阵规模，提高了活化计算的求解效率。

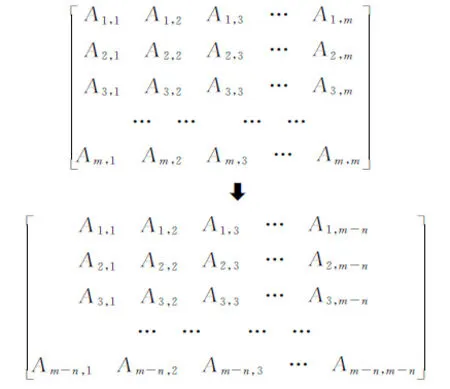
图2 大规模矩阵自适应降阶方法示意图

Fig.2 Schematic diagram of the mass matrix adaptive order reduction method

3 测试与验证

为了验证所发展的活化计算方法的正确性，本文选用IAEA-ACB国际基准例题[22]以及压水堆包壳材料例题[23]进行了测试，选取FISPACT-II作为参考程序。

3.1 IAEA-ACB国际基准例题

IAEA-ACB国际基准例题旨在验证活化计算程序的四个方面：(1)正确读取活化数据库的能力；(2)在多步长的计算中，活化程序的计算结果与基准值偏差不超过5%；(3)正确处理轻质量核素(H、He等)；(4)正确处理数据库中的同质异能核素。该国际基准例题包括Fe和Cr两个子例题，覆盖了常见的中子活化反应和衰变反应类型。根据初始条件，Fe的质量为1kg，Cr的核子密度为1.0E+20cm-3，辐照时间均为一年，中子通量谱参见文献[22]。本文的活化计算结果与基准值的相对误差参见图3和图4。

图3 Fe的活化产物核子密度相对误差Fig.3 The relative difference of activation of Fe calculation results

图4 Cr的活化产物核子密度相对误差Fig.4 The relative difference of activation of Cr calculation results

从图3和图4可知，由活化链动态构建方法得到的核素种类与基准值列出的核素种类一致。对于Fe和Cr两个子例题，经大规模矩阵自适应降阶方法处理后的矩阵求解效率相对于处理前的矩阵求解效率分别提高了1.82倍和2.11倍。同时本文在同质异能核素(52mMn、58mMn、44mSc、45mSc)、轻质量核素(1H、2H、3H等)、中等质量核素(Fe、Cr、Mn、Ni等)等活化计算中常见核素的计算结果与基准值的相对误差均低于0.5%，验证了本文发展的大规模矩阵自适应降阶方法的精确性。59Co和59Ni的计算结果与基准值相对偏差较大，分别为0.75%和0.71%，但中子活化过程中这两种核素的密度非常小，与初始核素密度相差1015～1018，对于实际工程中的影响非常小。总体来看，本文的计算结果与基准值的相对偏差远低于基准例题中要求的5%，满足基准例题中对活化计算程序的精度要求。

3.2 压水堆燃料包壳材料例题

压水堆燃料包壳材料是反应堆的重要材料之一，其材料的活化水平直接影响到燃料包壳的寿命与堆芯安全设计。本文以压水堆燃料包壳材料锆合金N18为例，首先通过蒙卡输运计算得到燃料包壳的中子通量分布，然后开展N18材料的活化计算分析与验证。N18材料初始元素组成如表1所示，辐照方案参见文献[23]。

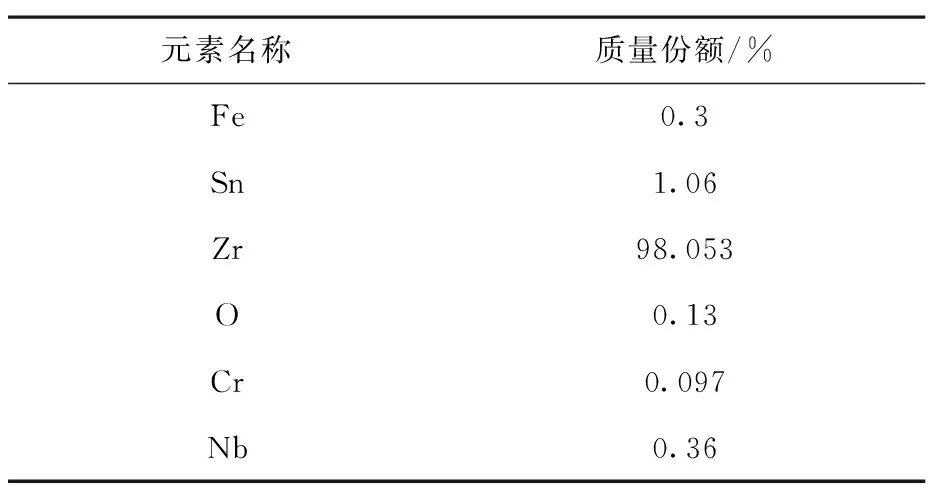
表1 新型锆合金N18的元素组成Table 1 The composition of new zirconium alloy N18

图5给出了本文和FISPACT-II分别计算包壳材料在停堆后12个冷却时段的活度分布，其计算结果随时间的衰减趋势完全一致。同时经大规模矩阵自适应降阶方法处理后的矩阵求解效率相对于处理前的矩阵求解效率提高了1.56倍。在停堆初期，包壳材料的活度约为1015Bq。在停堆后的一个月内，包壳材料的活度衰减缓慢，未出现量级变化，在此期间，包壳材料的活度主要受到核素89mY(T1/2=1.56e×10-1s)和89Zr(T1/2=2.82×105s)的影响。在停堆一个月至104年内，包壳材料的活度依次受到核素117mSn(T1/2=1.17×106s)、119mSn(T1/2=2.53×107s)和117mSn(T1/2=1.17×109s)的影响而出现量级衰减。停堆104年后，包壳材料的活度衰减程度趋于平缓。由图6可知，本文的计算结果在12个冷却时段与FISPACT-II的相对偏差均低于0.04%，验证了本文发展的活化计算方法的正确性。

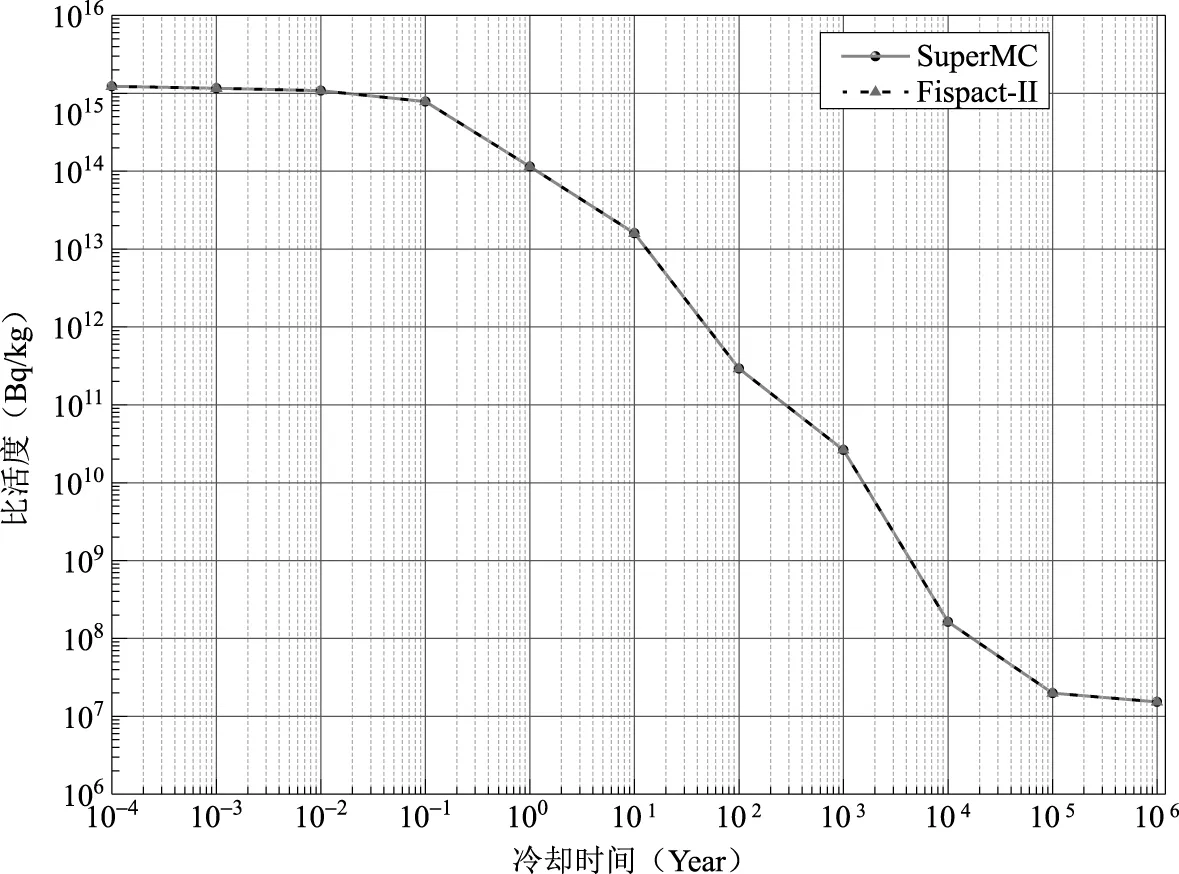
图5 新型锆合金N18活度计算结果Fig.5 The activity results of new zirconium alloy N18

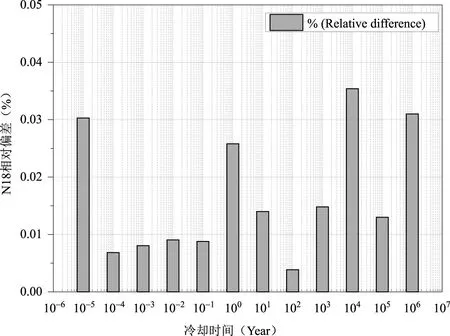
图6 新型锆合金N18活度计算结果相对误差Fig.6 The relative difference of new zirconium alloy N18 calculation results

4 结语

本文基于超级蒙卡核模拟软件系统SuperMC，采用切比雪夫有理逼近方法，进行了活化计算的研究，并对活化链构建等关键问题的处理方法进行了优化，发展了基于深度优先搜索的活化链动态构建方法和大规模矩阵自适应降阶方法。通过对IAEA-ACB国际基准例题及压水堆燃料包壳材料例题验证，初步证明了本文所实现活化计算方法的有效性与正确性，并且测试结果表明，本文发展的大规模矩阵自适应降阶方法能够有效提高矩阵的求解效率。本文活化计算方法的更多验证与应用研究将在后续工作中开展。

致谢

本文开展研究工作中，得到了FDS团队其他成员的大力帮助和支持，在此深表感谢！

[1] Cetnar J.General solution of Baterman equations for nuclear transmutations[J].Annals of nuclear Energy，2006，33：640-645.DOI：10.1016/j.anucene.2006.02.004.

[2] Croff A G.A user’s manual for ORIGEN2 computer code[R].Oak Ridge National Laboratory，1980.DOI：10.2172/5285077.

[3] Pusa M，Leppanen J.Computing the matrix exponential in burnup calculations[J].Nuclear science and engineering，2010，164(2)：140-150.

[4] Wu Y，Song J，Zheng H，et al.CAD-based Monte Carlo program for integrated simulation of nuclear system SuperMC[J].Annals of Nuclear Energy，2015，82(1)：161-168.DOI：10.1016/j.anucene.2014.08.058.

[5] Wu Y，FDS Team.CAD-Based Interface Programs for Fusion Neutron Transport Simulation.Fusion Engineering and Design，2009，84(7-11)：1987-1992.DOI：10.1016/j.fusengdes.2008.12.041.

[6] Y.Li，L.Lu，A.Ding，H.Hu，Q.Zeng，S.Zheng，Wu Y.Benchmarking of MCAM4.0 with the ITER 3D Model.Fusion Engineering and Design，2007，82：2861-2866.DOI：10.1016/ j.fusengdes.2007.02.022.

[7] Wu Y，FDS Team.Conceptual Design Activities of FDS Series Fusion Power Plants in China.Fusion Engineering and Design，2006，81(23-24)：2713-2718.DOI：10.1016/j.fusengdes.2006.07.068.

[8] L.Qiu，Wu Y，B.Xiao，Q.Xu，Q.Huang，B.Wu，Y.Chen，W.Xu，Y.Chen，X.Liu.A Low Aspect Ratio Tokamak Transmutation System.Nuclear Fusion，2000，40：629-633.DOI：10.1088/0029-5515/40/3Y/325.

[9] Wu Y，J.Jiang，M.Wang，M.Jin，FDS Team.A Fusion-Driven Subcritical System Concept Based on Viable Technologies.Nuclear Fusion，2011，51(10)：103036.1-7.DOI：10.1088/0029-5515/ 51/10/103036.

[10] Wu Y，FDS Team.Conceptual Design and Testing Strategy of a Dual Functional Lithium-Lead Test Blanket Module in ITER and EAST.Nuclear Fusion，2007，47(11)：1533-1539.DOI：10.7538/yzk.2015.49.S0.0007.

[11] Wu Y，FDS Team.Fusion-Based Hydrogen Production Reactor and Its Material Selection.Journal of Nuclear Materials，2009，386-388：122-126.DOI：10.1016/j.jnucmat.2008.12.075.

[12] Wu Y，FDS Team.Design Status and Development Strategy of China Liquid Lithium-Lead Blankets and Related Material Technology，2007，367-370：1410-1415.DOI：10.1016/j.jnucmat.2007.04-031.

[13] Wu Y，J.Qian，J.Yu.The Fusion-Driven Hybrid System and Its Material Selection.Journal of Nuclear Materials，2002，307-311：1629-1636.DOI：10.1016/S0022-3115(02)01272-2.

[14] Q.Huang，Wu Y，J.Li，et al.Status and Strategy of Fusion Materials Development in China.Journal of Nuclear Materials，2009，386-388：400-404.DOI：10.1016/j.jnucmat.2008.12.158.

[15] Q.Huang，J.Li，Y.Chen.Study of Irradiation Effects in China Low Activation Martensitic Steel CLAM.Journal of Nuclear Materials，2004，329：268-272.DOI：10.1016/j.jnucmat.2001.04.056.

[16] Y.Li，Q.Huang，Wu Y，T.Nagasaka，T. Muroga. Mechanical Properties and Microstructures of China Low Activation Martensitic Steel Compared with JLF-1.Journal of Nuclear Materials，2007，367-370：117-121.DOI：10.1016/j.jnucmat.2007.03.012.

[17] Wu Y，FDS Team.Design Analysis of the China Dual-Functional Lithium Lead (DFLL) Test Blanket Module in ITER.Fusion Engineering andDesign，2007，82：1893-1903.DOI：10.1016/j.fusengdes.2007.08.012.

[18] Wu Y，Xie Z，Fischer U.A discrete ordinates nodal method for one-dimensional neutron transport calculation in curvilinear geometries[J].Nuclear Science and Engineering，1999，133(3)：350-357.DOI：10.1016/j.anucene.2013.10.018.

[19] Wu Y，Zheng S，Zhu X，Wang W，et al.Conceptual Design of the Fusion-Driven Subcritical System FDS-I[J].Fusion Engineering and Design，2006，81 (Part B)：1305-1311.DOI：10.1016/j.fusengdes.2005.10.015.

[20] Wu Y，FDS Team.Conceptual design of the china fusion power plant FDS-II[J].Fusion Engineering and Design，2008，83(1)：1683-1689.DOI：10.1016/j.fusengdes.2008.06.048.

[21] Jean-Christphe C.Sublet，et al.The FISPACT-II User Manual[R].Culham Centre Fusion Energy，UK，2014.

[22] E.T.Cheng，et al.Report on the second international activation calculation benchmark comparison study[R].Austria，1994.

[23] Han Wenjing.Numerical Study and Preliminary Application of Activation Method Based on CRAM [D].North China Electric Power University，2015.

Researchand Verification of Activation Calculations Basedon Chebyshev Rational Approximation Method

ZHANG Bin-hang1，2，HAO Li-juan1，GE Peng1，SONG Jing1，PENG He1

(1.Institute of Nuclear Energy Safety Technology，Key Laboratory of Neutronics and Radiation Safety，
Chinese Academy of Sciences，Hefei of Anhui Prov.230031，China，2.University of Science & Technology of China，Hefei of Anhui Prov.230027，China)

A large number of neutrons are produced in nuclear reactor operation.These neutrons cause strong activation on structural materials and corrosion products，which is main radiation source on persons working on operation，maintenance and decommission.It is essential to develop activation calculation with high precision and high efficiency for the reactor design and safety analysis.Compared with the traditional activation calculation algorithm，Chebyshev rational approximation method has the advantages of computing efficiency，high precision，longtime step calculation and no need to deal with short-lived nuclides separately.In this paper，based on SuperMC，Cheyshev rational approximation method was adopted to study activation calculation，and dynamic construction method of activation chain and adaptive order reduction on massive matrix method were developed.Benchmark cases of IAEA-Activation Calculation Benchmark and PWR-Cladding Materials Case were used to validate the method.The calculation results have good agreements with reference values，which demonstrated the correctness of the activation calculation method of this work.In addition，the reduction on massive matrix method can effectively improve the efficiency of the matrix calculation.

Activation; Chebyshev rational approximation method; SuperMC; Activation chain;

2016-12-06

国家自然科学基金(11305203)、国家磁约束核聚变能发展研究专项(2014GB1120001)、中国科学院国防科技创新基金项目(CXJJ-16Q 231、CXJJ-15M037)，产业化基金

张彬航(1989—)，男，湖北荆州人，博士研究生，主要从事活化计算方法及程序研发工作

何 鹏：peng.he@fds.org.cn

TL329.2

A

0258-0918(2017)01-0065-08