基于GA的Tokamak聚变堆芯参数优化方法研究

孙 林，陈德鸿，王明煌，蒋洁琼

(1. 中国科学院核能安全技术研究所，中子输运理论与辐射安全重点实验室，安徽合肥230031；2.合肥工业大学电子科学与应用物理学院，安徽合肥230009)

基于GA的Tokamak聚变堆芯参数优化方法研究

孙 林1，2，陈德鸿1，王明煌1，蒋洁琼1

(1. 中国科学院核能安全技术研究所，中子输运理论与辐射安全重点实验室，安徽合肥230031；2.合肥工业大学电子科学与应用物理学院，安徽合肥230009)

托卡马克(Tokamak)聚变堆芯参数优化设计是聚变及聚变驱动次临界堆设计的重要步骤之一。本文发展了基于遗传算法(GA)的堆芯参数优化方法并与中国科学院核能安全技术研究所·FDS团队研发的系统程序SYSCODE堆芯物理模块相耦合，对堆芯参数进行优化。通过优化指定的聚变堆芯设计参数(如几何尺寸、等离子体电流、环向磁场等)，并满足给定的约束条件，使得单个或多个目标达到全局“最优”，对于堆芯设计具有一定参考价值。

Tokamak聚变堆芯；遗传算法；优化

中国科学院核能安全技术研究所·FDS团队开发了聚变反应堆设计参数优化与经济性分析软件SYSCODE[1-3]，用于聚变堆以及聚变裂变混合堆电站的经济性评估和系统分析，其主要计算功能包括聚变堆芯物理参数计算、聚变堆(及混合堆)工程参数计算、聚变堆(及混合堆)电站经济参数计算等，并提供参数优化、灵敏性分析模块用于设计参数的优化和分析[4-5]。

Tokamak聚变堆芯设计首先从简单的零维模型入手，即不考虑各物理量的空间分布和时间演变，也不考虑许多重要的物理过程，旨在获得体积平均和量级概念上的初步设计参数，为进一步详细设计指明方向和提供依据。

零维聚变堆芯参数主要有几何参数大半径R、小半径a、拉长比κ和三角变形δ，以及等离子体电流IP、环向磁场BT、归一化比压βN及Greenwald密度份额等[6-8]。不考虑各参数在磁面上的分布和随时间的演化，优化堆芯参数，在满足一定的条件下(如安全因子q值，βN的Troyon极限等)，实现堆芯性能“最佳”(如较高的聚变功率和较长的能量约束时间)是进行堆芯设计时需要考虑的重要方面[9-10]。

目前，求解聚变堆芯“最佳”性能及对应的设计参数有两种方法，一种是将研究的设计参数在变化区间内按一定步长全面正交组合，求取每一种组合对应的性能指标值，建立庞大的数据库，再利用约束条件进行筛选，如美国的ASC系统模型就是采用这种方法[11]。这种寻优方法的缺点是：样本数庞大、样本离散度大，人们难以从纷繁的离散样本中做出正确的判断，且常遗漏部分优良解。另一种方法是根据性能指标与单个设计参数之间简单的关系曲线，判断相对“最佳”性能指标值及对应的设计参数值，但这种方法需要对每个设计参数进行多次尝试。显然，该方法耗时、费力，且未必能够找到“最佳”性能指标及对应的设计参数；并且，该方法只适应一定条件下单一性能指标的优化，忽略了各设计参数之间的交互作用，具有明显的局限性。

遗传算法(Genetic Algorithm，GA)是一种在复杂解空间进行有向随机搜索的方法，具有良好的全局搜索能力，不会陷入局部最优解的快速下降陷阱；搜索过程既不受优化函数的连续性约束，也没有优化函数导数必须存在的要求；采用一种自适应搜索技术，其选择、交叉、变异等运算都是以一种概率方式来进行， 从而增加了搜索过程的灵活性。而聚变堆芯物理参数的计算，涉及的参数关系复杂、非线性以及不定的参数优化需求，采用遗传算法能够很好满足这些要求。建立适应聚变堆芯参数优化的遗传算法，利用遗传算法超强的寻优能力，能够快速求解一定约束条件下优越堆芯性能指标及对应的设计参数。因此，相对传统的设计方法，利用遗传算法求取堆芯“最佳”性能指标，便于堆芯设计时做出更快速、准确的判断，对于指导设计安全、经济、可行的聚变堆芯具有重要意义。

1 SYSCODE聚变堆芯模型

稳态、自洽和零维的等离子体模型包括：平衡稳定性、粒子与能量平衡和电流驱动等计算模型[12-13]。基于该设计理念，建立SYSCODE系统程序堆芯模型的主要依据如下：

1.1 等离子体MHD稳定性条件

95%磁面上安全因子q95是反映磁流体稳定性的重要指标，与等离子体中心磁场BT(T)、等离子体电流IP(MA)关系密切，并最终影响等离子体大、小半径R、a以及拉长比κ、三角变形因子δ等参数的设计，具体关系如(1)式所示：

(1)

1.2 等离子体密度和βN值的限制条件

堆芯等离子体除氘氚气体外，还包含α粒子及少量杂质，假设nD=nT，由电中性条件，得到D-T粒子密度：

nDT=ne(1-Zimp×fimp)-2×nHe

(2)

ne为体积平均的电子密度(1020m-3)，Zimp为杂质平均电荷数，fimp为杂质份额，则等离子体中总粒子：

nTOT=ne-nHe-ne(Zimp-1)×fimp

(3)

电子密度线平均密度要求满足Greenwald极限：

(4)

fGW为Greenwald份额，密度、温度沿小半径分布近似为：

(5)

式中：αn，αT分别代表密度、温度剖面指数。则环向比压：

(6)

式中：Te为密度权重的体积平均温度。

归一化比压：

(7)

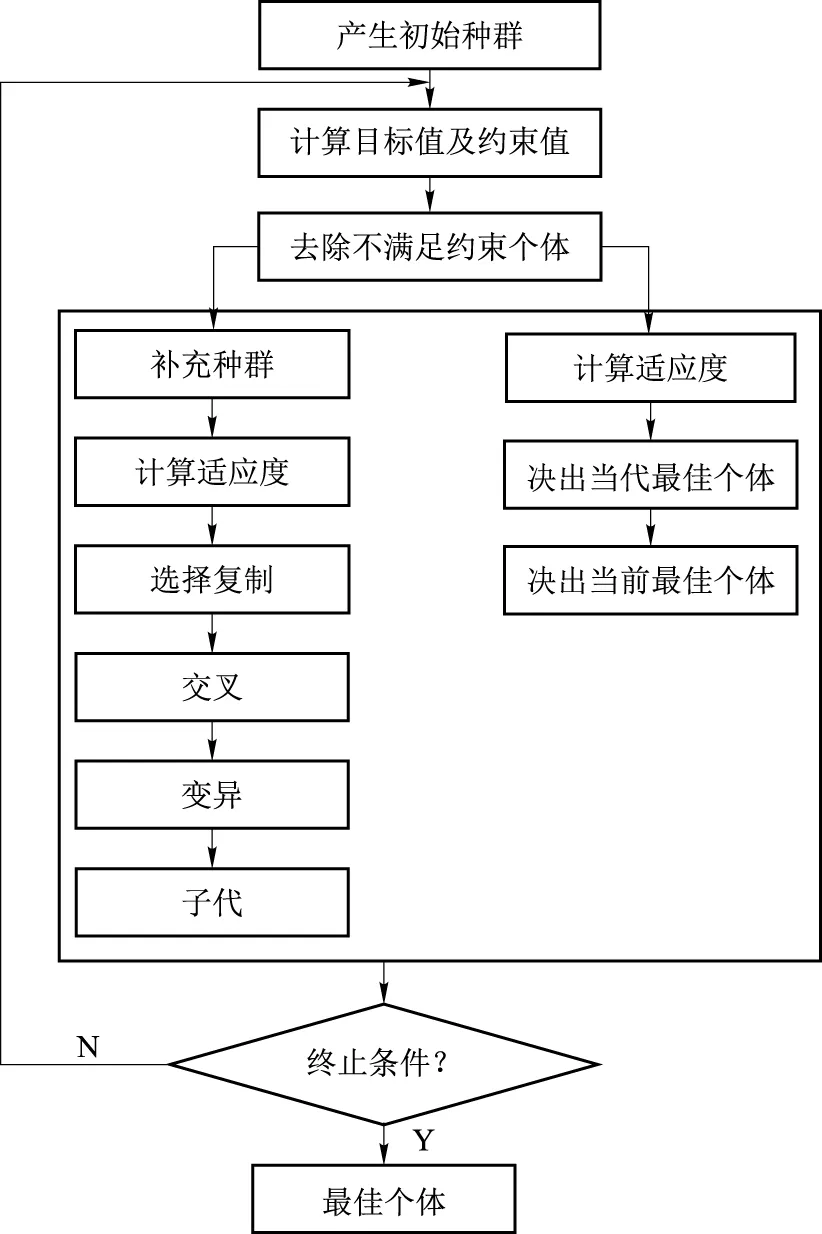
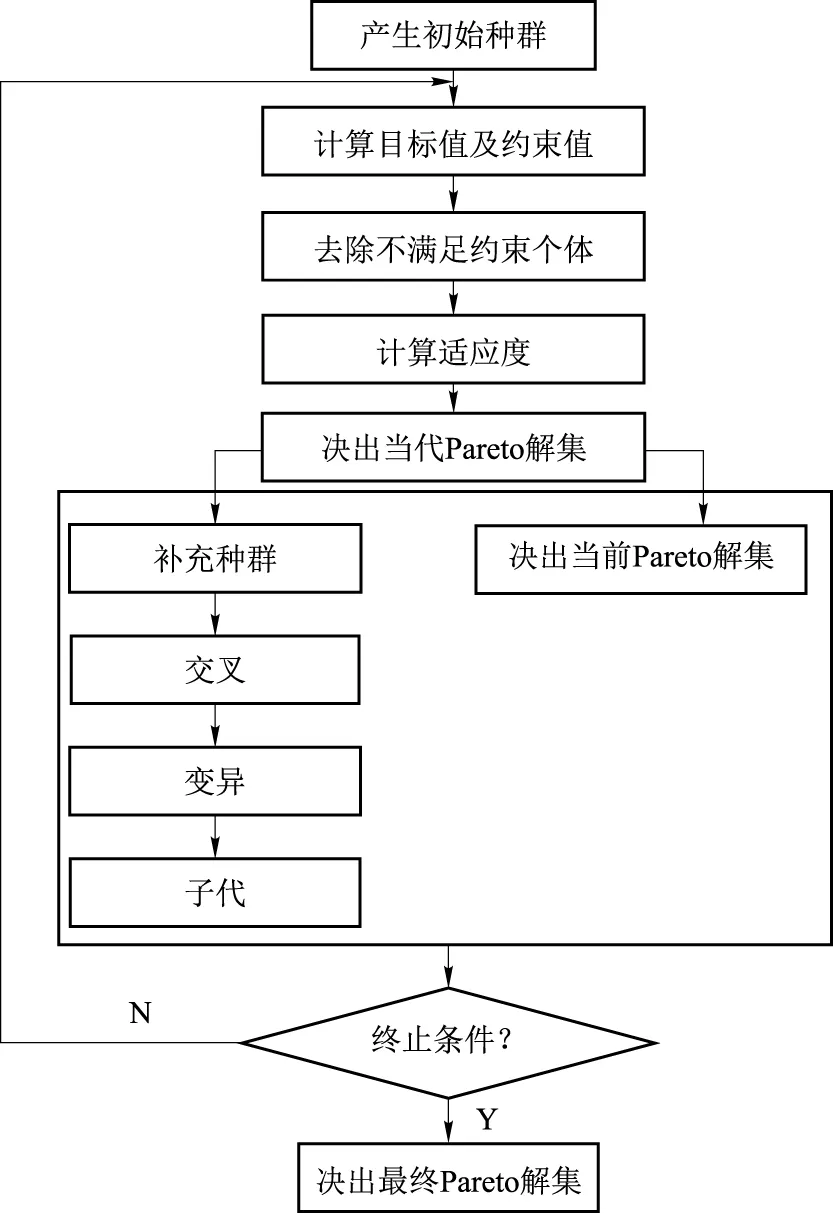
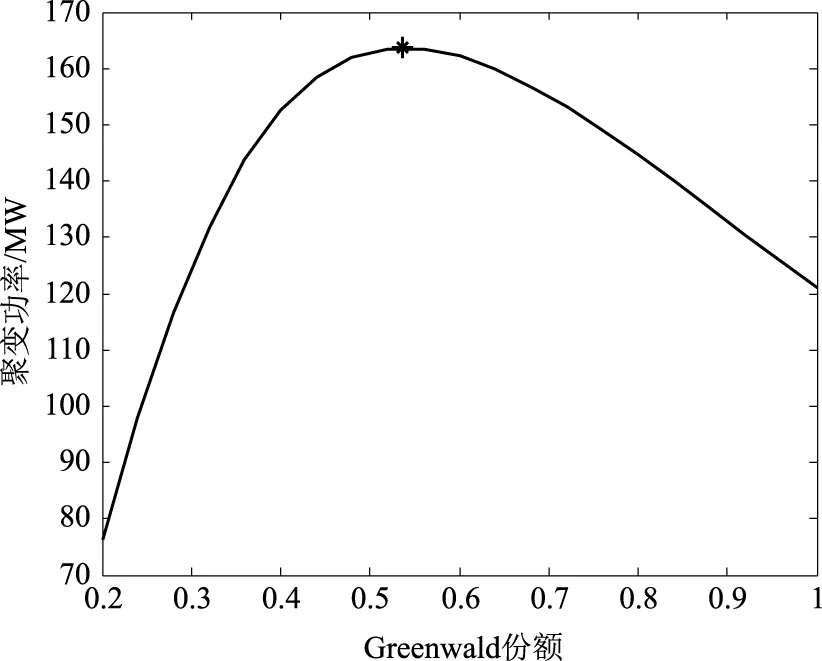
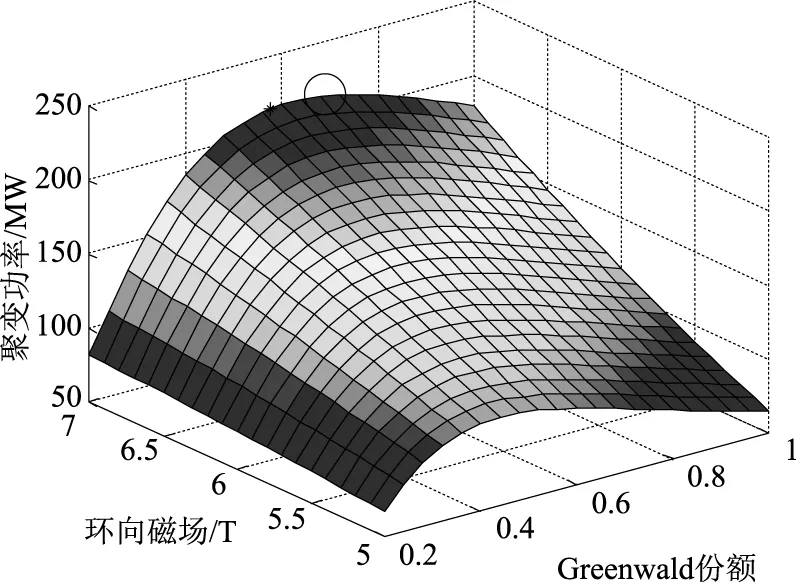
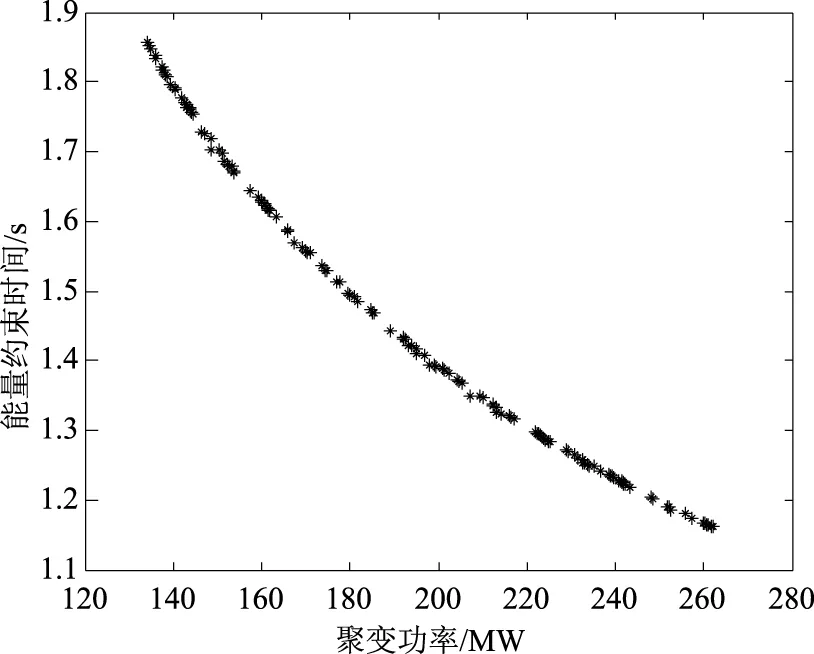
磁流体稳定性要求βN满足Troyon极限，一般地，βN

1.3 等离子体功率平衡

等离子体总能量：

(8)

聚变功率：

Pf=nDnT〈δv〉EDTV

(9)

式中：〈δv〉为氘氚聚变反应率，EDT为一次氘氚反应所释放的能量，V为等离子体体积。

α粒子功率：

(10)

辐射功率：

(11)

式中：Zeff为有效电荷数，c3=5.35×10-43，当系统稳定运行时，堆芯功率保持平衡，

Pα+PAUX=PLOSS+PRAD

(12)

式中：PAUX是辅助功率，用于驱动等离子体电流和加热等离子体；PLOSS是等离子体输运损失功率：

PLOSS=WTOT/τE

(13)

式中：能量约束时间采用ITER-98P(y，2)定标[15]：

(14)

2 遗传算法

遗传算法是一类借鉴生物界进化规律(适者生存，优胜劣汰遗传机制)演化而来的随机化搜索方法[16-17]，具有搜索灵活、求解快速和适应范围广等优点，已被人们广泛地应用于组合优化、机器学习、信号处理、自适应控制和人工生命等领域[18-19]。根据聚变堆芯物理实际特点及优化需求，建立适合的遗传优化模型，能够解决SYSCODE系统程序物理模型复杂的非线性、多变量、多目标优化问题，对于聚变堆芯优化设计具有重要参考作用。

2.1 单目标优化

单目标遗传算法用以寻求单个优化目标的最佳值(最大值、最小值或期望值)，同时满足一定的约束条件。一般地，可按图1来构造单目标优化的遗传算法。

需要指出的是：1) 当种群因去除不满足约束条件的个体规模减小时，需补充新个体，以保证种群规模，延续进化；2) 从未经补充的种群寻求当代最佳个体，最终的最佳个体即是从每代最佳个体中决出。

2.2 多目标优化

多目标优化的优化目标是具有k(k>1)个目标函数的集合，同时包含m个约束条件，目标函数和约束条件都是自变量的函数[20]。

y=f(x)=(f1(x)，f2(x)，…，fk(x))

Subject to：e(x)=(e1(x)，e2(x)，…，em(x))

Where：x=(x1，x2，…，xn)∈X

y=(y1，y2，…，yn)∈Y

(15)

多目标优化就是寻求满足所有约束条件e(x)并且使得f(x)最优的解。但是，对于多目标优化，通常最优解不止一个，而是一个最优解集即Pareto解集[21]。多目标遗传算法的目标是构造非支配集(non-dominated solutions)。

图1 单目标优化的流程图Fig.1 Flow chart of single objective optimization

并使非支配集不断逼近最优解集，最终达到最优。一般地，可按图2来构造多目标优化的遗传算法。

需要指出的是：1) 种群首先要去除不满足约束的个体，还需去除支配解，因此充新个体可以放在去除支配解后进行；2) 将每代的Pareto解保留在一独立单元，每增加一代，都去除支配解，保留并得到最终的非支配解。

图2 多目标优化的流程图Fig.2 Flow chart of multi-objective optimization

3 优化结果和分析

SYSCODE建立较为普适的聚变反应堆模型，文本采用FDS-I的堆芯设计参数作为参考例题，对所建立的优化模块的功能进行验证。FDS-I是中国科学院核能安全技术研究所·FDS团队设计的聚变驱动次临界堆，其主要堆芯物理参数分别为：大半径为4m、小半径为1m、Greenwald份额为0.75、三角变形为0.4、拉长比为1.78、归一化比压为3、等离子体电流为6.3MA，环向磁场为6.1T，能够实现150MW的聚变功率。

3.1 单目标优化

图3为单变量、单目标优化优化结果示意图。设计参数Greenwald份额的取值范围设为0.2～1，其他堆芯设计参数保持不变，优化目标为聚变功率的最大值。遗传算法的种群个数为100，运行代数为50代，交叉概率为0.6，变异概率为0.01，下面例题中算法本身参数取值与其相同。图中曲线为聚变功率随Greenwald份额的变化关系曲线，“*”表示优化求取的聚变功率最大值点(0.5229，163.5664MW)。

图3 FDS-I聚变功率随Greenwald份额变化关系曲线及最大值解Fig.3 Relationship curve of fusion power and Greenwald portion of FDS-I and maximum fusion power spot

与图3相同的是，图4中曲线也为聚变功率随Greenwald份额的变化关系曲线，但优化目标为聚变功率的150MW期望值，图中“*”表示优化求取的聚变功率150MW期望值点(0.7500，150.0301MW)。

图4 FDS-I聚变功率随Greenwald份额的变化关系曲线及期望值解Fig.4 Relationship curve of fusion power and Greenwald portion of FDS-I and expectant fusion power spot

图5为多变量、单目标优化优化结果示意图。设计参数Greenwald份额取值范围为0.2～1.0，环向磁场的取值范围5～7T，其他堆芯设计参数保持不变，优化目标为聚变功率的最大值。图5中，“*”(图中圆圈内)表示优化求取的聚变功率最大值点(0.5889，6.9785T，214.2170MW)，曲面为聚变功率随Greenwald份额和环向磁场的变化关系。

图5 FDS-I聚变功率随Greenwald份额和环向磁场的变化关系曲面及最大值解Fig.5 Relationship surface of fusion power between Greenwald portion and toroidal magnetic field of FDS-I and maximum fusion power spot

3.2 多目标优化

单(或多)变量、多目标优化，即是在一定范围内改变单(或多)设计参数的取值，求取多个(两个或以上)优化对象的相对最优值，实际上，由于多个优化对象在逼近目标时往往不同步(甚至反方向)，如一个优化对象在逼近目标值时，另一个优化对象可能正在远离其目标值，某个优化对象达到最优而别的对象却非最优，因此，多目标优化往往不存在所谓的最优解，只能得到所谓的帕累托解集；然而，得到的帕累托解集对于选择相对最优解具有指导意义。

图6 FDS-I聚变功率与能量约束时间帕累托解图Fig.6 Pareto figure of fusion power and energy confinement time of FDS-I

图6为多目标优化结果示意图。优化目标求取聚变功率的最大值和能量约束时间最长，设计参数环向磁场的取值范围5～7T，等离子体电流的取值范围5～7MA，其他堆芯设计参数保持不变。图6中，横坐标为聚变功率，纵坐标为能量约束时间。

3.3 结果分析

由图3可知，在其他设计参数取恰当值不变时，聚变功率与Greenwald份额并非成简单的单调关系，这是因为增加Greenwald份额(电子密度)虽然会提高反应率(有助于提高聚变功率)，但同时也会降低等离子体温度(降低聚变功率)；求取聚变功率最大值作为优化目标，寻优结果位于曲线的最高点，说明优化模块与堆芯物理模块耦合后能够很好地运行，且优化结果具有较高的精度。

如图4，将聚变功率150MW的期望值作为优化目标，寻优结果也具有较高的精度；需要指出的是，虽然根据图中曲线，应存在2个点与150MW聚变功率相对应，但优化模块所求取的最优解是唯一的，这种唯一的优化结果往往会导致其他最优解被遗漏，因此，对于优化目标与设计参数非单调的情况，应关注优化结果多样性的问题。

图5为聚变功率与Greenwald份额、等离子体电流两个设计参数之间的变化关系图。三维曲面图，不仅反映了设计目标与设计参数之间的关系，同时反映了两个设计参数之间的交互作用对设计目标的影响；表示优化结果的“*”处于曲面的最高点，也说明优化结果的可靠性。

图6为聚变功率、能量约束时间t两个优化目标的优化结果示意图。由于聚变功率、能量约束时间与等离子电流、环向磁场的变化趋势不一致，得不到所谓的最优解，只能得到如图6所示的Pareto解集。曲线上的每一个点“*”即表示一组解。基于Pareto解集，设计人员依据专家经验，综合考虑反应堆的可行性、可靠性、经济性等因素综合选取一组适合的解。

4 结束语

遗传优化算法具有良好的可操作性能、全局寻优性能，根据聚变及聚变驱动次临界堆系统程序SYSCODE聚变堆芯物理模块的实际特点，本文建立了与之相匹配的遗传优化算法模型并与之耦合。结果表明，两模块耦合后运行效果良好，且求解结果精确可靠，较好地解决了堆芯物理设计的参数选取问题。

但是，为了便于说明问题，文中所例举的优化实例，涉及的设计参数、优化目标较少，能够给出二维或三维图形。在堆芯物理实际设计过程中，涉及的参数、设计目标数量多且相互之间作用机理复杂。笔者通过验证，当多个设计参数和优化目标时，优化模型仍能够得到正确的优化解集；但是，优化结果为多维空间的多个离散点，难以用图的形式直观表现，也增加了选取适合的“最优解”的难度。

SYSCODE是一个从物理到工程再到经济学参数计算的系统程序。其在进行经济学计算和系统分析的过程中，工程计算和经济计算也需要优化模块提供参数优化功能。而工程计算和经济计算的模型和各个参数之间的影响关系更加复杂。如何将遗传优化算法应用到整个SYSCODE的物理、工程和经济模块，实现对整个反应堆乃至整个电站设计参数的优化是未来需要进一步开展的工作。

[1] Y. Wu， FDS Team.Conceptual design activities of Fusion-Driven Subcritical System FDS-I[J]. Fusion Engineering and Design，2006，81： 1305-1311.

[2] Y. Wu， FDS Team.Conceptual design activities of FDS series fusion power plants in China[J]. Fusion Engineering and Design，2006，81： 2713-2718.

[3] Y. Wu， FDS Team. Conceptual design of the China fusion power plant FDS-II[J]. Fusion Engineering and Design，2008，83(10-12)：1683-1689.

[4] 黄德所， 吴宜灿， 胡丽琴.基于最小化发电成本的聚变驱动次临界堆参数优化分析[J]. 核科学与工程， 2004， 24(4)： 356-365.

[5] 黄德所， 等. 聚变驱动次临界堆经济性分析[J]. 核科学与工程， 2004， 24(2)： 184-196.

[6] Y. Wu， J. Jiang， M. Wang， et al. A fusion-driven subcritical system concept based on viable technologies [J]. NUCLEAR FUSION， 2011(51)：1-7.

[7] 汪晖，陈德鸿，段文学，等. 基于常规托卡马克的多功能聚变工程实验堆堆芯初步设计与分析[J]. 核科学与工程.

[8] Y.Wu， FDS Team Conceptual Design and Testing Strategy of a Dual Functional Lithium-Lead Test Blanket Module in ITER and EAST[J]. Nuclear Fusion， 2007，47(11)：1533-1539.

[9] Chen YX， Wu YC.Conceptual study on high performance blanket in a spherical tokamak fusion-driven transmitter[J]. Fusion Engineering and Design， 2000，49-50：507-512.

[10] Yican Wu. Progress in Fusion-driven Hybrid System Studies in China[J]. Fusion Engineering and Design， 2002，63-64：73-80.

[11] Carlson. L， Tillack. M， Najmabadi. F. Development， Visualization， and Application of the ARIES Systems Code[J]. IEEE TRANSACTIONS ON PLASMA CIENCE. 2012，Vol. 40，No. 3：552-556.

[12] 吴宜灿，柯严，郑善良，等. 聚变驱动次临界堆概念设计研究[J]. 核科学与工程，Vol. 24，No. 1：72-80.

[13] 储德林，吴斌，吴宜灿，等. 聚变驱动次临界堆聚变堆芯参数设计与分析[J]. 核科学与工程，Vol. 24，No. 1：81-86.

[14] Jardin S C， Batke C G.，et al. Physics basis for a tokamak fusion power plant[J]. Fusion Engineering and design， 2000，48：281-298.

[15] R. Aymar， P. Barabaschi. Y， Shimomura. The ITER design[J]. Plasma Phys.Control.Fusion，2002，Vo1.44， No.5：519-565.

[16] 肖伟平，何宏. 基于遗传算法的数据挖掘方法及应用[J]. 湖南科技大学学报(自然科学版)，2009，24(3)：82-86.

[17] 张士杰.聚变电站经济学分析系统的研发与应用研究[D]. 中国科学院研究生院博士学位论文，2007：50-51.

[18] 马永杰，云文霞.遗传算法研究进展[J]. 计算机应用研究，2012，Vol.29,No.4：1201-1210.

[19] 黄冀卓，王湛，马人乐.一种新的求解约束多目标优化问题的遗传算法[J]. 计算机工程与应用，2006(23)：47-51.

[20] J F Aguilar Madeira， H Rodrigues， HeitorPina. Multi-objective optimization of structures topology by genetic algorithms[J]. Advances in Engineering Software，2005(36)：21-28.

[21] 谢涛，陈火旺，康立山.多目标优化的演化算法[J]. 计算机学报，2003，26(8)：998.

Study on the Method of Parameters Optimization for Tokamak Fusion Reactor Core Based on GA

SUN Lin1，2， CHEN De-hong1， WANG Ming-huang1， JIANG Jie-qiong1

(1. Key Laboratory of Neutronics and Radiation Safety， Institute of Nuclear Energy Safety Technology， Chinese Academy of Sciences， Hefei of Anhui Prov. 230031， China；2.School of Electronic Science and Applied Physics， Hefei University of Technology， Hefei of Anhui Prov. 230009， China)

It is an important step for fusion reactor and fusion-fission hybrid reactor to parameters optimization for Tokamak fusion reactor core. A parameter optimization procedure for fusion reactor core based on genetic algorithm(GA) was developed and coupled with reactor core physics model of SYSCODE which has been developed by FDS team， and is used for optimizing reactor core parameters. With adjusting the value of reactor core parameters such as geometric parameters， plasma current， toroidal magnetic field and so on， this optimization method can obtain global “optimum solution” about single or multiple objectives and which can provide reference value for design of fusion reactor core.

Tokamak fusion reactor core； Genetic algorithm； Optimization

2016-12-27

国家自然科学基金支持项目(11205194)，国家自然科学基金(11105174)，合肥工业大学校基金支持项目(2013HGXJ0194)

孙 林(1976—)，男，安徽人，博士后，现从事核能科学与工程方面研究

陈德鸿：dehong.chen@fds.org.cn

TL46

A 文章编号：0258-0918(2017)01-0073-07