线性微分约束可积充要条件的简捷证明

曹小杉 师俊平

(西安理工大学土木建筑工程学院工程力学系,西安710048)

线性微分约束可积充要条件的简捷证明

曹小杉1)师俊平

(西安理工大学土木建筑工程学院工程力学系,西安710048)

线性微分约束，也称Pfaf f约束是工程领域中常见的一种微分约束，其可积性是判断该约束是否为完整约束的准则.许多分析力学教材和研究非完整系统的教材都给出了 Pfaf f约束可积的充要条件但并未证明.本文给出了Pfaf f约束可积的充要条件的简捷证明方法，仅采用高等数学中所授场论部分的基本内容，供分析力学课程教学的教师和学习相关课程的学生参考.

Pfaf f约束,可积性,充分必要条件

前言

在分析力学理论中，研究完整系统和非完整系统常常采用完全不同的方法，尤其是有些动力学方程和原理仅仅适用于完整系统[1-2].那么，确定研究对象属于完整系统或非完整系统是首要环节.只要系统中存在非完整约束，则该系统就属于非完整系统.非完整约束，是指不可积分的微分约束.因此，判断微分约束的可积性在分析力学理论中具有十分重要的意义.

线性微分约束，也称Pfaf f约束，是工程中常见的一种微分约束，导弹追踪问题、纯滚动问题等都属于线性微分约束.凡是涉及到非完整系统动力学问题的教材中都给出了Pfaf f约束可积的充要条件，但是大多证明从略[1-3].即便追溯到1977年的文献，也仅仅是对 Pfaf f约束可积条件在特定条件下的充分性予以说明[4].2012年北京大学陈滨在所著《分析动力学》中详细地讨论了 Pfaf f约束的可积性定理[5].该著作对单个Pfaf f约束方程的可积性分两个变元、三个变元和多个变元进行了详细的讨论.针对两个变元、三个变元的情况，利用构造法，给出了积分曲面的形式，从而证明其定理的充要性.但对于多个变元的情况，也是略去了证明.与微分几何相关的数学书籍也针对Pfaf f方程进行讨论，其主要思路为先定义微分流形，引入切空间的概念，给出Frobenius定理，再进一步证明Pfaf f方程可积性的充要条件[6-8].

在分析力学教学过程中，首先讲授约束和约束类型，突然引入一个略去证明而数学形式较为复杂的定理，学生觉得难以理解.尽管在几个典型例题之后，学生能够靠记忆掌握求解该类问题的基本方法，但不符合力学类课程逻辑严密的特点.而微分几何教材中的证明方法，相关基础的概念非常庞杂，可能几个学时都无法介绍清楚，并不适合力学课程的教学，这或许也是力学类教材中该部分证明从略的原因.本文采用高等数学基本知识，直接给出多个变元条件下定理的必要性；而对于定理的充分性，基于前人已经严格证明的两个变元Pfaf f约束可积，利用数学归纳法，并引入一个简单定理，予以证明.这种Pfaf f约束可积的充要条件简捷证明方法，可供喜欢探究力学问题来龙去脉的学生参考.

1 Pfaf f约束可积的充要条件

设一个力学系统由n个质点构成，受到线性Pfaf f约束为

其中Ψi，A均是各质点位置的函数，˙ri表示的是第i个质点的速度.在直角坐标系中有

为了便于表示，将不再区分位形变量和时间变量，得到线性微分约束的统一形式.

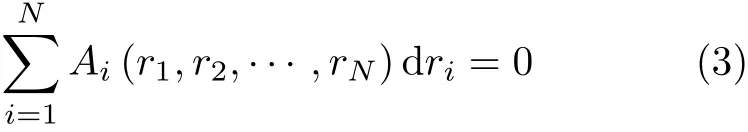
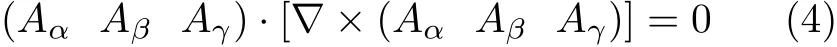
2 必要性证明

设方程(3)可积，则存在一个等效方程

其中U=U(r1,r2,…,rN)，为一个待求的连续可导函数.

由式(5)得到

如果式(3)和式(6)为等效方程，则

其中Φ=Φ(r1,r2,…,rN)，其倒数就是数学中的积分因子.

2.1 分量形式的证明

将式(7)代入式(4)，从而得到

从而命题的必要性得证.

2.2 场量形式的证明

对于U=U(r1,r2,…,rN)，任意取α,β,γ，如果仅选用α,β,γ对应的rα,rβ,rγ为变量，其余的ri并不参与到求偏导数的计算.可将U=U(r1,r2,…,rN)看作是BZ_85_1584_1354_1214_1254=BZ_85_1584_1354_1214_1254(rα,rβ,rγ),相对应的是一个三维坐标系的量，简化形式为

由场论的基本性质有[9]

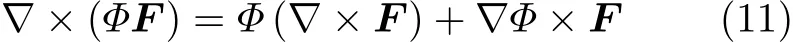
其中Φ是一个标量，而F是任意一个向量.进而，如果F是一个量的梯度，则有

这也就是通常所述的梯度场是无旋场[9].

将式(10)代入式(11)，并考虑性质(12)可以得到

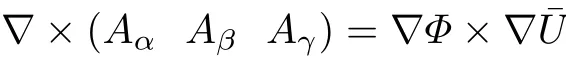
代入式(4)得到

显然，向量∇BZ_85_1584_1354_1214_1254与∇Φ×∇BZ_85_1584_1354_1214_1254垂直，且两个垂直向量的点积为零.从而命题的必要性得证.

3 充分性证明

采用数学归纳法，即需证明：

如果对于N-1的情况，由对于任意α,β,γ满足 (AαAβAγ)·[∇×(AαAβAγ)]=0，方程必然可积这个命题成立；那么对于N的情况，由对于任意α,β,γ满足 (AαAβAγ)·[∇×(AαAβAγ)]=0，方程也必然可积.

首先，如果对于式(4)中N=2时，式(4)自动满足，方程也必然可积[5].其可积性在很多教材中都有说明，此处不再赘述.

如果将Ai(r1,r2,…,rN)中rN看作是常数，函数自变量维数由N个降为N-1个，新函数为i(r1,r2,…,rN).

那么如果满足(AαAβAγ)·[∇×(AαAβAγ)] =0，那么也必然满足

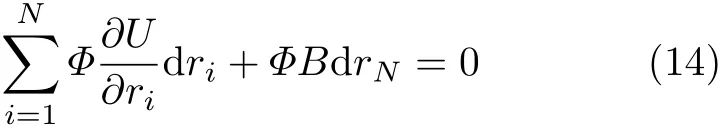
其中B=B(r1,r2,…,rN)为一待定函数，Φ=Φ(r1,r2,…,rN)，U=U(r1,r2,…,rN)，满足

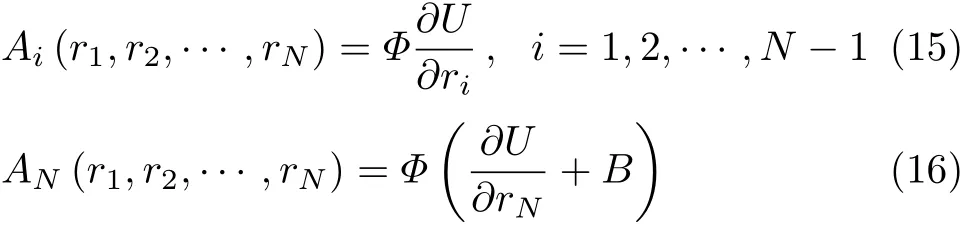
那么对于任意不同且不等于N的α,β

代入式(4)左半部分得到

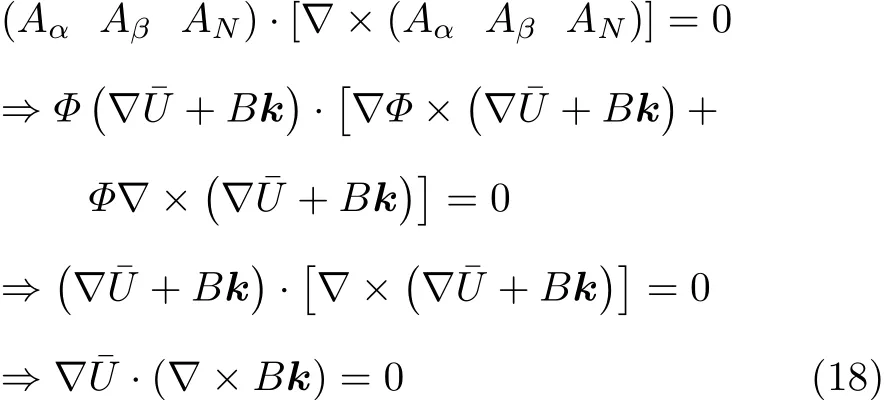
情况1：如果∇×Bk=0可得

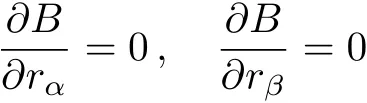
从而得到B与rα,rβ无关.同理可得B与ri,i=1,2,…,N-1无关.则令=(rN)=B/Φ，代入式(14)得到

则式(3)的等效式可由式(19)得到

式(20)可以积分为

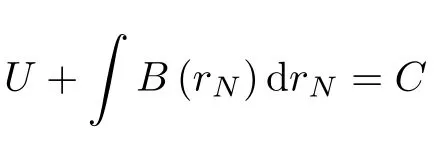
则式(3)可积.

情况2：如果∇×Bk/=0，可得∇·(∇×Bk)= 0

引理：对于两个函数u1(r1,r2,…,rN),u2(r1,r2,…,rN)中任意α,β，满足α,β/=N,那么u1可以表示为u1=F(u2,rN)

由该引理可得，函数B可以表示为U和rN的函数，那么式(14)可以简化并得出

显然方程(21)中仅含两个变量，由于含两个变量的线性微分约束必然可积，则该方程可积.

引理的证明：

对于两个函数u1(r1,r2,…,rN),u2(r1,r2,…,rN)，不失一般性，u1可以表示为

那么由链导法可得

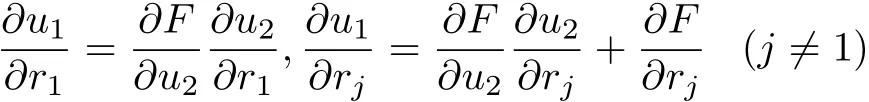
4 结论

本文中，Pfaf f约束可积充要条件的证明仅仅运用了高等数学中场论部分的基础知识，便于学生理解.相对而言，必要性证明更加简单.必要性的命题是：如果可积，那么式(4)成立.对应的逆否命题是：如果式(4)不成立，那么不可积.学生采用这个逆否命题就可以判断不可积的微分约束.教学中，建议可以给出必要性证明，但具体采用分量表示形式还是梯度表示形式，可由学生整体的高等数学基础决定.

1 梅凤翔.分析力学(上卷).北京：北京理工大学出版社，2013

2 叶敏，肖龙翔.分析力学.天津：天津大学出版社，2001

3 梅凤翔.非完整系统力学基础.北京：北京工业学院出版社, 1985

4 Rosenberg RM.Analytical Dynamics of Discrete Systems. New York：Pleum Press,1977

5 陈滨.分析动力学.北京：北京大学出版社，2012

6 威尔顿霍尔兹.数学物理中的微分形式.叶以同译.北京：北京大学出版社，1990

7 陈省身，陈维恒.微分几何讲义.北京：北京大学出版社，2001

8 梅向明，黄敬之.微分几何.北京：人民教育出版社，1981

9 埃伯哈德·蔡德勒等.数学指南——实用数学手册.李文林等译.北京：科学出版社，2012

(责任编辑：胡 漫)

O316

A

10.6052/1000-0879-16-092

2016-03-22收到第1稿，2016-03-30收到修改稿.

1)曹小杉,教授，博士生导师，主要研究方向为智能材料结构中的弹性波.E-mail：caoxsh@xaut.edu.cn

曹小杉,师俊平.线性微分约束可积充要条件的简捷证明.力学与实践,2017,39(1)：79-82

Cao Xiaoshan,Shi Junping.A simple method to prove the necessary and sufficient conditions of integrability for linear dif f erential constraints.Mechanics in Engineering,2017,39(1)：79-82