高分子溶液弹性失稳教学实验平台开发及应用1)

贾永霞 彭 杰

(清华大学航天航空学院工程力学系，北京100081)

高分子溶液弹性失稳教学实验平台开发及应用1)

贾永霞2)彭 杰

(清华大学航天航空学院工程力学系，北京100081)

在低雷诺数下，忽略惯性影响的黏弹性流体中存在的非线性应力可以引发湍流现象.在流体力学的教学过程中，为了让学生对此有直观认识，设计制作了黏弹性流体实验台.采用高速摄影的方法，对流体由弹性失稳而引起的流态变化过程进行观测.在教学实践中发现，该实验台操作简单，能够非常直观地对流体弹性引起的流动失稳过程进行显示.通过学生自己动手实践，极大地加深了对流体弹性效应引起的流动失稳过程的理解.

黏弹性流体，弹性失稳，流动显示

引言

在高雷诺数流动情况下，牛顿流体会发生失稳并最终发展为湍流.然而对于黏弹性流体，即便在流动雷诺数很低(如低流速、小尺度)的情况下，也会有流动失稳现象发生，此时流动呈现出不规则运动形态，相应的流动阻力显著增加，流动已表现出充分发展的湍流特征.前者源于高雷诺数下流场中较大的雷诺应力，也称为惯性湍流；而后者流动雷诺数较低，引起流动失稳的原因是黏弹性流体中高分子团拉伸所产生的弹性应力，故称为弹性湍流.换句话说，惯性湍流是由流体运动的基本控制方程，即Navier-Stokes方程的非线性特性引起，而弹性湍流则是由流体本构方程的非线性特性引起[1].

通常情况下，黏弹性流体的非线性力学性质主要表现为较大的外延黏性和韦森伯效应，其非线性程度可由韦森伯数Wi=V λ/L来表示，它反映了流体特征时间和弛豫时间之比，其中V是流动的特征速度、λ是黏弹性流体的弛豫时间、L为流动的特征尺度.Wi值越大，则流体的力学性质的非线性程度 (或黏弹性效应)也就越强.此时，即使流体运动的基本方程是线性的(如低雷诺数情况下流体运动的 Stokes方程)，流体的非线性力学特性也会引起流动失稳进而产生湍流[2].对于低雷诺数情形，黏弹性流体的弹性效应足够大时，即当参数Wi/Re=λν/L2较大时，流动可发生失稳并产生弹性湍流.这里Re=V L/ν是流动的雷诺数，ν为流体的运动学黏性系数.在本教学实验中将通过观测旋转平板间的黏弹性高分子溶液的流场结构，获得黏弹性高分子溶液在低雷诺数流动情况下的弹性流动失稳现象的直观认识，从而加深对流体弹性效应引起的流动失稳过程的理解.

式中，F为扰动变量，α为径向波数，m为整数，σ为扰动增长率.m=0表示轴对称扰动，描述径向嵌套涡结构；m/=0表示非轴对称扰动，对应于螺旋涡结构.因此，通过观察流场中出现的涡结构，即可对流动是否发生失稳以及失稳后的状态进行判断.在实验测试中，CCD阵列获取的图像中任何一个像素的光强变化可表示为[4]

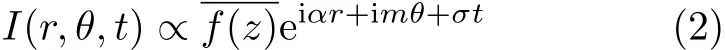
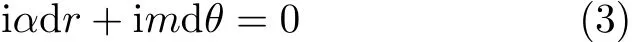
对方程(3)积分，可以得到

方程(4)给出二次流中涡结构的空间位置，它可以通过阿基米德螺旋线进行描述[5]，如图1所示，给出了径向波数α固定，周向波数m取值分别为0,1和2的情况.因此，在实验中可以通过观察流场中出现阿基米德螺旋线结构，对流动的失稳以及失稳后的状态进行直观判断.

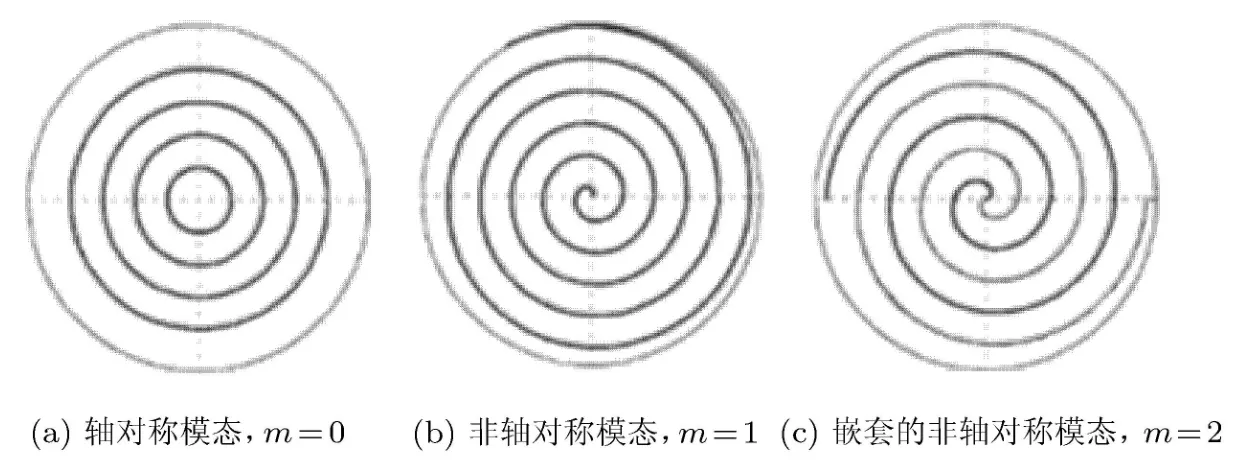
图1 由式(4)给出的阿基米德螺旋线的形式[4]

1 实验平台与装置

为了在实验中观察到黏弹性流体如图1所示的阿基米德螺旋线结构.我们设计并建造了图2所示教学演示实验装置.其中上圆盘与圆杯底面的半径分别是R=35mm和R1=40mm，两者间距为d=10mm.d/R=0.286.较大的弯曲程度促使剪切流失稳，在低剪切率下产生二次流.静止的圆杯底面与上圆盘同轴，同轴电机带动上圆盘旋转.圆杯侧壁和底面是透明的有机玻璃.填充的液体高度d=10mm，上板刚刚接触液体表面，特殊的遮盖以防止液体蒸发.在圆杯的下边放置一个45°的反射镜，采用CCD相机进行高速摄影，对圆杯内流体的流动结构演化情况进行拍摄.为了降低背景噪声，上圆盘的下底面涂黑.在实践中，根据实际情况，也可采用数码相机替代高速摄像机，对流场结构进行观测.

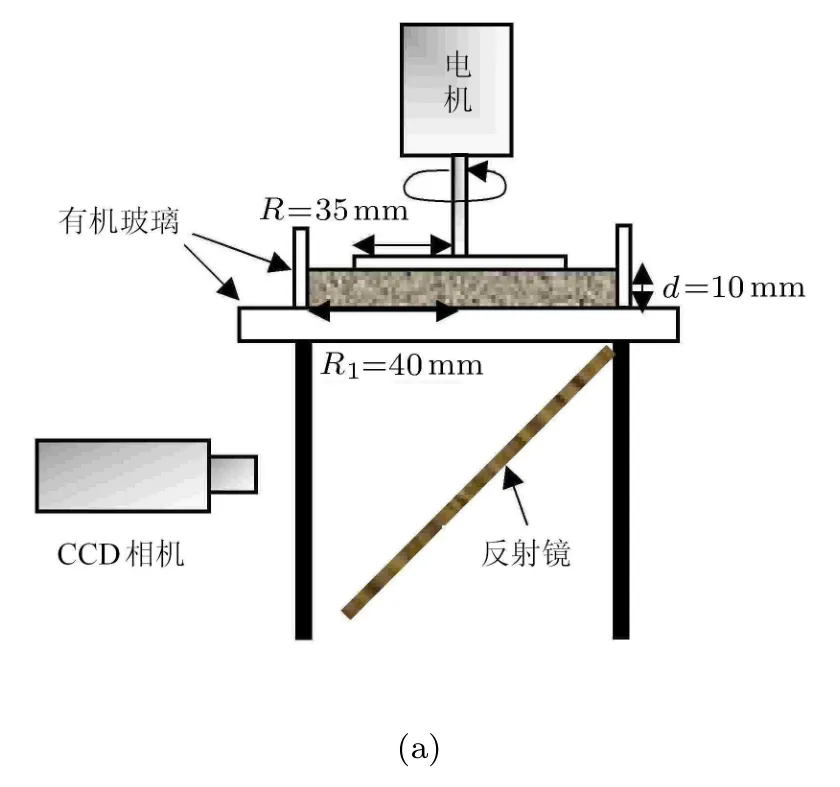
图2 实验装置简图及三维立体图

2 实验方案及测试方法

首先，本实验中黏弹性流体可通过在溶剂中添加聚丙烯酰胺获得.具体配比过程如下：

(1)在 25°C恒温情况下，采用 70%的蔗糖和1%的氯化钠水溶液作为溶剂.通过恒平NDJ-56型台式数显旋转黏度计可对其黏度进行测量，结果为ηs=0.23Pa·s.

(2)按重量计算添加聚丙烯酰胺，采用稀释的方法进行配比，使其质量分数约为8.0×10-5.所得黏弹性流体的表观黏度亦可通过黏度计进行测量，流体的弛豫时间λ则可以通过振动实验测试应力与剪切率之间的相位移进行估算，在本实验中其值约为λ=1.5s.

其次，为了能够通过CCD摄像机观察到流场结构，本实验采用的实验方法如下：

(1)在黏弹性溶液中播撒适当浓度的反光薄云母晶片示踪粒子，并且搅拌均匀.相比于染色液，云母晶片的优点在于流场中较小的幅值振荡便会影响云母晶片的运动方向，且不需要连续注入.

(2)在装置的周围使用激光片光照明，控制光源反射光量，采用高速相机拍摄高分子溶液中某一截面的流场信息，从而获得弹性失稳引起的流态转变过程的图像.

(3)改变上圆盘的旋转速率，采用高速CCD相机观察旋转剪切流动中的流动图像，获得不同剪切率下黏弹性流体的流动图像.

3 实验结果及讨论

在本实验中，采用了经典的流动显示技术.通过向黏弹性流体中添加各向异性云母晶片示踪粒子对流体运动轨迹进行追踪.在流动未发生失稳的情况下，反射光局部平均强度在空间均匀分布.然而，当流动发生失稳且流场中出现二次流结构时，反射光局部平均强度的空间分布将呈现不均匀性.此时，可以根据反射光强度在空间分布及其随时间的演化规律，推测流场中存在的二次结构及其演化规律.

图3 黏弹性流体在不同韦森伯数下的弹性失稳过程的流动图像(其中，云母片尺寸范围是100µm～150µm)

在实验过程中，我们选取了两种不同尺寸的云母晶片作为流动显示的示踪粒子.图3给出云母晶片尺寸范围是100µm～150µm时，黏弹性流体在不同韦森伯数和雷诺数下拍摄到的流动图像.从中可以看出，此时流场内的二次流动结果不明显.这说明，此时云母晶片尺寸较大，对流动的跟随性不够强，所以无法对流动结构进行很好的呈现.同样，在粒子图像测速技术(particle image velocimetry，PIV)中也存在类似问题.通常，在连续加速的流体中粒子的滞后速度Us可表示为[6]

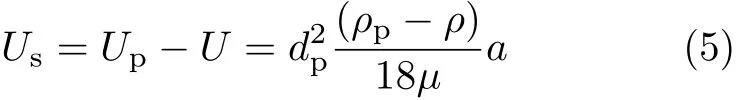
其中，Up为粒子的速度，ρ为流体的密度，ρp为示踪粒子的密度，dp为粒子的直径，µ为动力黏度，a为加速度.从式(5)可知，由于流体与示踪粒子间存在密度差，示踪粒子的直径应非常小以保证对流体运动的极好跟随性；另一方面，考虑到示踪粒子的光散射特性，粒子直径也不能太小.我们选择不同尺寸(20µm～50µm)范围的云母晶片，在图3所示相同工况下再次进行实验，结果如图4所示，从中可以明显观察到黏弹性溶液流动失稳过程的典型流动图像.其中图4(a)显示反射光局部平均强度呈现空间均匀分布，这表明流动是稳定的均匀剪切流；随韦森伯数和雷诺数的逐步增加，此时流场内的剪切速率随之增大，流动发生失稳，反射光局部平均强度空间分布不均匀，这表明流场中出现二次流空间结构，流动由均匀剪切流动转变为具有较大尺度的带状旋涡结构，如图4(b)所示，此时旋涡呈轴对称状态，这与图1(a)轴对称模态相应；随韦森伯数和雷诺数的进一步增大，轴对称涡结构再次发生失稳，并演化为图4(c)所示的非轴对称单一螺旋线状态，这与图1(b)所示非轴对称模态相对应.继续增大韦森伯数和雷诺数，Wi≥14时，流场呈现嵌套螺旋线状态，如图4(d)所示，这与图1(c)所示嵌套的非轴对称模态相对应.若继续增加韦森伯数和雷诺数，流动将进一步发生失稳，流场中出现不同尺度的流动结构，并最终发展为充分发展的非线性模态.此时观察到的流动图像呈现明显的不规则特性.

图4 黏弹性流体在不同韦森伯数下的弹性失稳过程的流动图像(其中，云母片尺寸范围是20µm～50µm)

牛顿流体中激发惯性湍流的速度与流体黏性成正比，而黏弹性流体的弛豫时间随着黏度的增加而成比例增加.弛豫时间尺度与系统的尺寸无关，如果实验平台参数d/R恒定，弹性湍流在某一个Wi数下产生.因此，通过选择更黏的黏弹性流体，即可在较低速度下激发弹性湍流.这里需要指出，仅改变上圆盘的旋转速率并不能改变参数Wi/Re=λν/L2，但通过配比不同百分比的蔗糖和氯化钠溶液，可以得到不同黏度的溶剂.通过改变聚丙烯酰胺的浓度，可以得到具有不同弛豫时间λ的黏弹性流体.

为了证明图4所示流动失稳过程是由流体弹性效应引起，在本实验中还进行了对比实验.图5给出了具有相同配比的蔗糖溶液(动力黏性系数相同)在未添加聚丙烯酰胺情况下的实验结果，其中各工况与图4所示工况一一对应.对比图4与图5可以发现，对于黏性流体，在本实验参数范围内，随韦森伯数和雷诺数的增加，反射光局部平均强度在空间上都呈均匀分布，这表明流动一直处于稳定的均匀剪切流状态，进一步也说明图4所示黏弹性流体的失稳主要是由于流体的弹性效应引起.

图5 黏性流体(未添加聚丙烯酰胺)的流动图像，与图(4)一一对应(其中，云母片尺寸范围是20µm～50µm)

4 结论与展望

搭建实验台并对黏弹性流体和黏性流体进行对比实验.通过流动可视化技术，对流场中的二次流结构进行观察，让学生对流体弹性效应引起流动失稳以及失稳以后的流场状态演化过程有了更为直观的认识.这有助于学生掌握黏弹性流体稳定性理论，进一步加深对非牛顿流体的流动特性及规律的认识.与此同时，本实验过程也为PIV测量黏弹性流体流场信息打下基础，未来可通过PIV测量，引导学生对弹性失稳的相关控制参数进行定量分析.

1 Shaqfeh ESG.Purely elastic instabilities in viscometric fl ows.Annual Review of Fluid Mechanics,1996,28(1)：129-185

2 Groisman A,Steinberg V.Elastic turbulence in a polymer solution fl ow.Nature,2000,405：53-55

5 Davis PJ.Spirals：From Theodorus to Chaos.Wellesley：A K Peters,1993

6 Ra ff el M,Willert CE,Wereley S,et al.Particle Image Velocimetry：a Practical Guide.Berlin：Springer,2013

(责任编辑：胡 漫)

O357.1，O353.5

A

10.6052/1000-0879-16-308

本文于2016-09-23收到.

1)清华大学实验室创新基金资助项目(53100200116).

2)贾永霞，博士，讲师，主要从事实验流体力学教学.E-mail：yongxiajia@tsinghua.edu.cn

贾永霞，彭杰.高分子溶液弹性失稳教学实验平台开发及应用.力学与实践,2017,39(1)：75-78

Jia Yongxia,Peng Jie.Experiment platform development of elastic instability in a polymer solution flow and teaching application.Mechanics in Engineering,2017,39(1)：75-78