模块度引导下的社区发现增量学习算法*

王宏杰，滕 飞+，李天瑞

1.西南交通大学 信息科学与技术学院，成都 611756

2.四川省云计算与智能技术高校重点实验室，成都 611756

模块度引导下的社区发现增量学习算法*

王宏杰1,2，滕 飞1,2+，李天瑞1,2

1.西南交通大学 信息科学与技术学院，成都 611756

2.四川省云计算与智能技术高校重点实验室，成都 611756

当前社区发现领域存在诸多静态社区划分算法，而其划分结果的不稳定性和较高的算法复杂度已经不能适应如今规模庞大，变化频繁的网络结构。为解决传统静态算法这一局限性，提出了一种利用模块度优化的增量学习算法，将网络结构的变化划分成边变化、点变化两种基本操作，在对“模块度最大化”的规则指导下实现网络结构的增量学习。实验表明，该算法在保证原有社区划分结果的前提下，可以将新变化的节点快速划分进已有社区，并使得模块度与静态算法重新计算模块度相近，节省了时间，保持了社区划分的实时性。

社区划分；增量学习；模块度

1 引言

近年来，随着Web应用的推广，对于其中包含的复杂网络结构也逐渐成为研究热点[1]。作为复杂网络结构的3个主要特征之一[2-4]，社区结构发现成为最受关注的研究方向，已在生物学、社会学和信息网络等领域得到了广泛应用。最早对于社区结构划分结果，人们往往以“内聚性强，外联性弱”等笼统直观感觉进行判断[5]，对社区划分结果并无统一评价标准。直到2004年，Newman提出了“模块度[6-9]”的概念，旨在将社区划分结果量化以便横向比较，人们才找到了一条社区划分的新途径。在模块度指导下，传统的社区划分问题被转化成单目标优化问题[10]，之后有不少领域内的研究者提出关于模块度的社区发现算法，例如Newman提出的基于模块度的簇聚类FN[11]方法，Blondel和Guillaume提出的FastUnfolding[12]方法，这些方法均达到了十分理想的分类效果。基于模块度的各类研究方兴未艾，然而随着现实中的网络结构越来越复杂，传统静态社区划分算法逐渐暴露出两方面的缺陷：一是划分效率低。FN算法复杂度达到O((m+n)n)，而FastUnfolding算法复杂度也达到O(kmn)，如果被应用到大规模网络结构中，很难保证社区划分的实时性。二是划分成本高。由于基于模块度的社区划分算法本质上属于优化算法，而优化算法的随机性使得每次算法执行之后的划分结果不一致，并且当前实时场景中的图结构变化越来越趋于局部性和碎片化[13-14]。例如社交网络中的好友关系[15-17]，每个人的朋友关系网一旦形成则很难发生大规模改变，而局部小圈子里好友增加，好友之间添加，删除联系的互动却是时常发生，此时若利用静态算法对社区重新划分则可能会对原有社区划分结果造成重大破坏，所有在原有划分结果上的研究与应用系统也会受到影响。因此未来研究的新趋势之一将会是网络结构的社区发现增量学习算法[18]。

本文在“模块度最大化”的划分指导原则下，提出一种新的社区发现增量学习算法。其核心思想是将社区的变化总结成4种常见基本操作，并与模块度相结合，针对每种变化设计了相应的增量学习过程。通过实验证明，这种基于模块度的增量学习算法有能力处理大规模社区数据，既能节省重新运用静态算法划分社区的时间，又能在不破坏大部分节点原有社区的基础上，使得新增节点的划分达到和静态算法相近的效果。

本文组织结构如下：第2章为相关工作；第3章介绍增量算法的具体实现流程；第4章给出了实验方案和实验结果；第5章为结束语。

2 相关工作

2.1 模块度

2002年Girvan和Newman联合提出了GN算法[19]。该算法每个执行流程都找到一条具有最大边介数的边，删除该条边后原图倾向于分成两个独立的联系不紧密的子网络，执行若干次该过程直到每个节点就是一个退化网络。这个过程中存在社区结构没有量化的缺陷，删除操作要到哪一步停止需要引入变量指导等问题。之后模块度被提出，作为网络结构中的一个性质，它能衡量一个图的划分是否合理[20-22]。目前模块度已成为社区划分领域一个非常重要的社区评价指标。对于一个社区而言，最理想的划分结果应是社区内部连接紧密，社区之间连接稀疏。当社区i≠j，用eij表示连接i、j两个社区的边数所占图中总边数比例的一半；当社区i=j，用eij表示社区i内部边所占图中总边数的比例。对于ai：

其中，C表示社区集合，则有模块度Q的表达式：

为了计算方便，现将式（2）变形：

其中，m是边总数；Ii是社区内部总边数；Di是社区内部节点总度数。

模块度所指代的实际物理含义指网络中连接社区结构内部顶点的边所占的比例与另一个随机网络中连接社区内部顶点的边所占比例的期望值相减得到的差值。这种差值越大，表明该划分下网络结构越优于随机划分，所得结果更有参考价值，更符合图社区要求。模块度介于0到1之间，划分结果大于0.4可以视为划分有意义。模块度是本文提出的增量算法的划分依据。

2.2 FastUnfolding算法

FastUnfolding算法是基于模块度的重要优化算法。设G为社会网络抽象出的图结构，V为G中点集，FastUnfolding算法提供一种划分方案将V划分为N个社区{C1,C2,…,Cn}，每个子集对应一个社区，最后使得图中。为使Q值最大，FastUnfolding算法将社区划分问题分层处理：第一层是原始图结构，之后每一层都是上一层找到最大Q值划分后合并相同社区节点产生的新图。在每层中，初始每个点都作为单独社区，之后对于每个点都考虑将其依次划分到与相邻点社区中所得到的Q值增益。Q值增益计算公式如下：

其中，ki,in是连接节点到目的社区中所有点的权重；ki是节点i的度数；Ic是社区内部边数；Dc是社区内部点总度数；m是图中总边数。在找到增益最大的邻居节点后，把归属社区改为邻居节点社区。把对图中所有节点完成划分操作当成一个阶段，迭代该阶段执行过程，直到没有一种新的划分会对图造成正向ΔQ，即完成一层的操作。图1为FastUnfolding算法流程实例图，每一层都要分为Q值优化和社区合并两个流程。

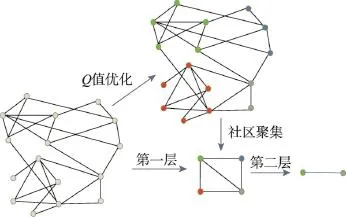
Fig.1 Procedure of FastUnfolding图1 FastUnfolding算法流程

该算法复杂度为O(kmn)，其中m为边数，n为点数，k为图划分的层级。FastUnfolding算法对于静态图有着很好的处理效果，时间耗费也随着层级的累积呈几何式下降，是目前算法复杂度最低的社区发现算法。但是FastUnfolding算法的缺陷在于由于每一层中的点归属划分操作次序随机，导致针对一个图进行多次划分后划分结果均不一致。实验表明，当图结构越复杂，点边数越多，划分结果差别越大。如此性质导致算法只能用于社区划分的一次性静态批量处理，而对于图的结构变化频繁的增量社区环境中，FastUnfolding为代表的基于Q值的社区划分算法便不适用，否则仅由于小部分局部变化的节点便对图结构进行重新划分，导致原有社区划分遭受破坏。因而本文提出一种只针对局部变化节点处理的增量式扩展算法，能有效地解决这个问题。

3 基于模块度的增量式扩展算法

当图结构发生变化时，增量式算法保证原图大部分节点从属社区不变，利用现有社区作为划分依据，从而只对变化部分涉及的节点进行重新划分。针对基于模块度划分的社区，包含以下已知信息：

（1）社区数目w以及社区集合C={C1,C2,…,Cw}；

（2）社区内部总边数集合I={Ic1,Ic2,…,Icw}；

（3）社区的节点总度数D={Dc1,Dc2,…,Dcw}；

（4）图的总边数m，总节点数n。

根据式（3）可得各个社区的Q值。在上述信息基础上，将社区变化划分为两类：一类是点的变化；一类是边的变化。当点变化时，该点的邻居点度数发生变化，I值、D值变化；当边变化时，该边连接两个点的度数发生变化，I值、D值变化。因此无论哪类变化，社区Q值总会发生改变。不同的是有的变化需要对某些点重新划分社区，有的变化则不需要。

3.1 边变化

（1）社区之间减少边或社区内部增加边

如图2，社区之间连边减少，社区内部连边增加（黑色虚线表示删除，蓝色虚线表示增加，图3类似表示），此种情况处理方法较为简单。由于社区划分目的是达到社区之间联系松散的状态，故此类变化对已有社区划分结果起正向巩固作用，不会影响划分结果，只需在更新m、I、D值后即可通过式（3）重新计算Q值。

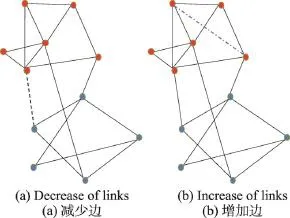
Fig.2 Decrease of links between communities and increase of links inside communities图2 社区之间边减少和社区内部边增加

（2）社区之间增加边或社区内部减少边

当社区内部减少边或社区之间增加边时社区结构变得松散，如图3、图4。由于边连接节点为社区边界节点，假设这些节点会发生社区归属变化，根据“模块度最大化”原则，将这些点分别改变社区后的模块度与保持在原有社区的模块度进行比较，比较结果作为改变依据，若Q值有增大则改变社区，若Q值减少则保持原有社区不变。

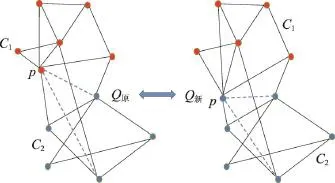
Fig.3 Increase of links between communities图3 社区之间增加边

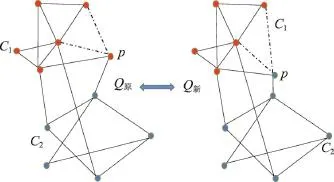
Fig.4 Decrease of links inside communities图4 社区内部减少边

算法1边变化处理算法

已知社区数目w，社区集合C，社区内部总边数集合I，社区内部总度数集合D，图的总边数m，总点数n，邻接矩阵A={aij}，增加边数据集Inc_Data={(ni,nj)}，考量节点为 p，Cneigh为p相邻社区。

3.2 点变化

删除点可以看作删除了跟一个点相关的所有边，本质上还是属于在社区中删除边，故具体方法可以参照3.1节中介绍。此节着重强调增加点这种情形。如图5，若增加点p与原图中t个社区有连接，则增量算法要求p依次加入到t个社区中，再分别计算加入后的模块度与原社区模块度的差值作为Q值增量，之后将p加入到Q值增量最大的社区中。

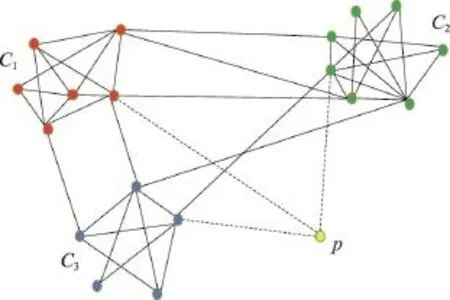
Fig.5 Increase of single vertex图5 社区增加单个点

算法2单个点变化处理算法

已知社区数目w，社区集合C，社区内部总边数集合I，社区内部总度数集合D，图的总边数m，总点数n，邻接矩阵A={aij}，增加边数据集Inc_Data={(ni,nj)}，考量节点为 p，Cneigh为p相邻社区。

若一次增加多个节点，如图6所示，可将新增点分为两类：一类节点与原社区有连接；二类节点没有连接。在处理此类问题时，需要先将所有与原社区有连接的点，运用上述增加点的方法加入到已有社团中，并更新原有社区的社团结构，更新之后的结果如图7和图8。

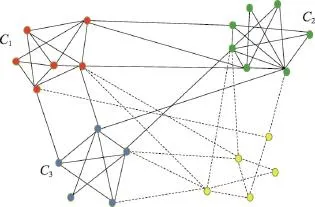
Fig.6 Increase of a group of vertexes图6 社区增加多个点

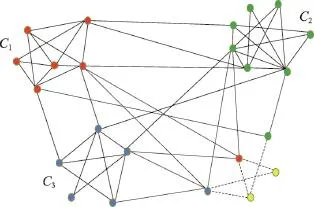
Fig.7 Communities of Class I vertexes detected图7 一类节点划分完成

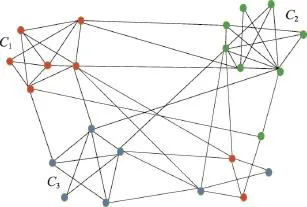
Fig.8 Communities of Class II vertexes detected图8 二类节点划分完成

算法3批量点变化处理算法

已知社区数目w，社区集合C，社区内部总边数集合I，社区内部总度数集合D，图的总边数m，总点数n，邻接矩阵A={aij}，增加边数据集Inc_Data={(ni,nj)}，考量节点为p，Cneigh为 p相邻社区。

4 实验结果及分析

本文的实验部分首先针对边变化和点变化分别进行增量式算法的验证，再将点变化和边变化汇总验证，验证的方向主要包括增量式算法和静态算法在时间和效果上的比较。首先用静态算法得到划分结果，之后为了保证原图的结构不发生大的变化，从原图抽出数据作为增量数据集，运行增量算法再与静态算法的划分结果比较，由此得到的结果可以较客观地反映增量算法的运行效果。

4.1 Facebook交友数据集

Facebook数据集包括4 039个点，88 234条边。在用FastUnfolding算法作出划分后，可得到14个社区，模块度为0.835。

4.1.1 边变化

表1、表2分别记录了在Facebook数据集中，增加社区之间边和删除社区内部边时，运用增量学习方法得到的划分结果。表中可以对比看到静态算法重新划分时间和效果。

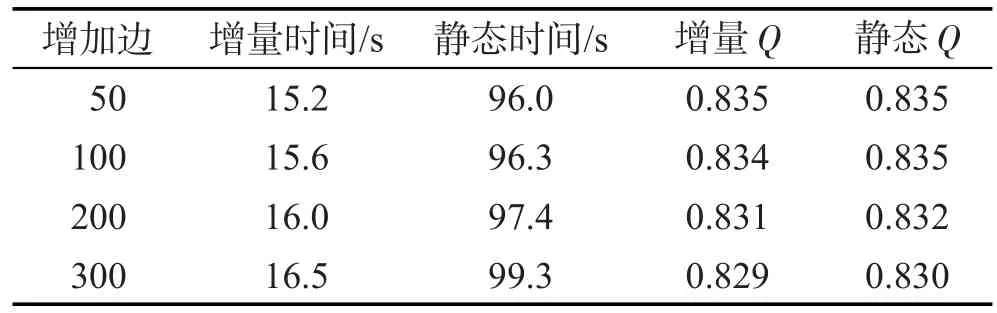
Table 1 Experiment of link changes(Increase)表1 边变化实验（增加边）

Table 2 Experiment of link changes(Decrease)表2 边变化实验（删除边）

4.1.2 点变化

表3记录了在随机抽取了1%～5%的节点后，将其作为增量数据点，加回到剩余图构成的社区中得到的增量算法的运行时间和结果，并与初始完整数据集静态算法的时间与结果进行比较。

Table 3 Experiment of vertex changes表3 点变化实验

4.1.3 综合变化

综合变化将点变化以及边变化汇总，在从原图抽取点再加回到剩余图这个过程中另加上边的变化，包括增加边、删除边。图9、图10显示了综合变化中，增量算法与静态算法的时间对比以及Q值误差的变化趋势。表4记录了Facebook数据集综合变化实验结果。

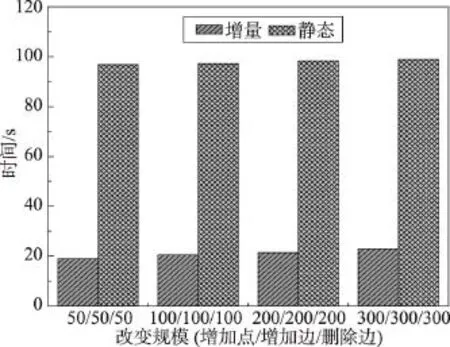
Fig.9 Contrast between time costs of synthetical changes图9 综合变化时间对比

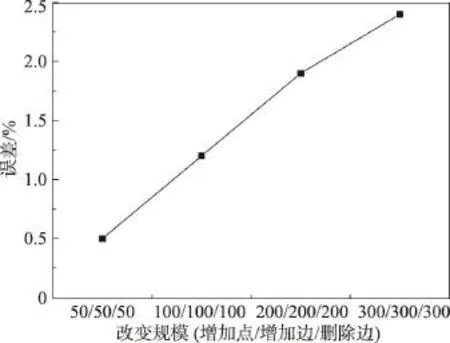
Fig.10 Contrast between error of synthetical changes图10 综合变化误差对比

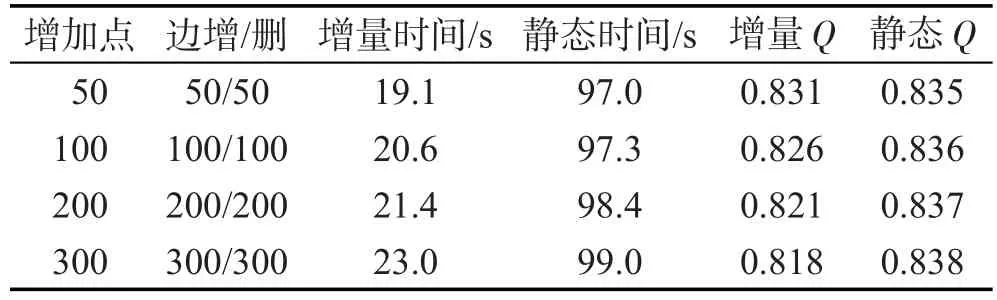
Table 4 Experiment of synthetical changes表4 综合变化实验

4.2 实验总结

通过Facebook数据集的实验可以说明增量算法的运行效果良好，算法依照的“模块度最大”原则能保证增量算法的划分方案可以达到与静态算法相近的效果，误差在5%之内；而在时间方面，增量算法耗时相较于静态算法也有3～4倍的减小。因而本文的增量算法既能满足提高划分效率要求，又能在不破坏原有社区划分的基础上使得增量点获得最好的划分归属，保证模块度最大，达到算法优化的目的。

5 结束语

为应对网络规模日益庞大的背景下传统静态社区划分算法不能很好地处理频繁小规模社区变化的社区归属问题，本文基于模块度的概念提出了一套处理社区4种基本变化的增量学习算法，在“模块度最大化”原则的指导下，变化节点划分进对整体网络模块度提升最大的社区里。实验证明，这种方法可以很好地应对较大规模数据集近1%～7%的动态变化，既提升了划分效率，又能保证模块度相差在可接受范围。然而本文算法尚存在一些不足，算法的学习过程是建立在社区数目不变的前提下，而实际情况中若社区的扩张达到一定规模，社区数量亦有可能随之变化。因此下一步的工作重点主要讨论在社区规模的持续增量而引起社区数量变化时如何设计合理有效的增量算法。

[1]Watts D J,Strogatz S H.Collective dynamics of“smallworld”networks[J].Nature,1998,393(6684):440-442.

[2]Newman M E J.The structure and function of complex networks[J].SIAM Review,2003,45(2):167-256.

[3]Bader D,Madduri K.SNAP,small-world network analysis and partitioning:an open-source parallel graph framework for the exploration of large-scale networks[C]//Proceedings of the 2008 IEEE International Symposium on Parallel and Distributed Processing,Miami,USA,Apr 14-18,2008.Piscataway,USA:IEEE,2008:1-12.

[4]Rosvall M,Bergstrom C T.An information-theoretic framework for resolving community structure in complex networks[J].Proceedings of the National Academy of Sciences of the United States ofAmerica,2007,104(18):7327-7331.

[5]Danon L,Díaz-Guilera A,Duch J,et al.Comparing community structure identification[J].Journal of Statistical Mechanics: Theory and Experiment,2005,9:P09008.

[6]Clauset A,Newman M E,Moore C.Finding community structure in very large networks[J].Physical Review E, 2004,70(6):066111.

[7]Newman M E J.Modularity and community structure in networks[J].Proceedings of the National Academy of Sciences of the United States of America,2006,103(23):8577-8582.

[8]Newman M E J,Girvan M.Finding and evaluating community structure in networks[J].Physical Review E,2004,69 (2):026113.

[9]Duch J,Arenas A.Community detection in complex networks using extremal optimization[J].Physical Review E,2005, 72(2):027104.

[10]Li Zhenping,Zhang Shihua,Wang Ruisheng,et al.Quantitative function for community detection[J].Physical Review E,2008,77(3):036109.

[11]Newman M E J.Fast algorithm for detecting community structure in networks[J].Physical Review E,2004,69(6): 066133.

[12]Blondel V D,Guillaume J L,Lambiotte R,et al.Fast unfolding of communities in large networks[J].Journal of Statistical Mechanics:Theory and Experiment,2008,10:P10008.

[13]Palla G,Derényi I,Farkas I,et al.Uncovering the overlapping community structure of complex networks in nature and society[J].Nature,2005,435(7043):814-818.

[14]Bu Zhan,Zhang Chengcui,Xia Zhengyou,et al.A fast parallel modularity optimization algorithm(FPMQA)for community detection in online social network[J].Knowledge-Based Systems,2013,50:246-259.

[15]Gong Maoguo,Zhang Lingjun,Ma Jingjing,et al.Community detection in dynamic social networks based on multiobjective immune algorithm[J].Journal of Computer Science and Technology,2012,27(3):455-467.

[16]Ahn Y Y,Bagrow J P,Lehmann S.Link communities reveal multiscale complexity in networks[J].Nature,2010,466 (7307):761-764.

[17]Yang J,Leskovec J.Defining and evaluating network communities based on ground-truth[J].Knowledge and Information Systems,2015,42(1):181-213.

[18]Polikar R,Upda L,Upda S S,et al.Learn++:an incremental learning algorithm for supervised neural networks[J].IEEE Transactions on Systems,Man,and Cybernetics:Part C Applications and Reviews,2001,31(4):497-508.

[19]Girvan M,Newman M E J.Community structure in social and biological networks[J].Proceedings of the National Academy of Sciences of the United States of America, 2002,99(12):7821-7826.

[20]Lin Youfang,Wang Tianyu,Tang Rui,et al.An effective model and algorithm for community detection in social networks[J].Journal of Computer Research and Development, 2012,49(2):337-345.

[21]Wang Li,Cheng Xueqi.Dynamic community in online social networks[J].Chinese Journal of Computers,2015,38 (2):219-237.

[22]Pinney J W,Westhead D R.Betweenness-based decomposition methods for social and biological networks[J].Interdisciplinary Statistics and Bioinformatics,2006:87-90.

附中文参考文献：

[20]林友芳,王天宇,唐锐,等.一种有效的社会网络社区发现模型和算法[J].计算机研究与发展，2012,49(2):337-345.

[21]王莉,程学旗.在线社会网络的动态社区发现及演化[J].计算机学报,2015,38(2):219-237.

WANG Hongjie was born in 1991.He is an M.S.candidate at School of Information Science and Technology, Southwest Jiaotong University.His research interests include cloud computing and community detection,etc.

王宏杰（1991—），男，西南交通大学信息科学与技术学院软件工程系硕士研究生，主要研究领域为云计算，社区发现等。

TENG Fei was born in 1984.She received the Ph.D.degree from Ecole Centrale Paris in 2011.Now she is a lecturer at Southwest Jiaotong University.Her research interests include cloud computing,distributed deployment and community detection,etc.

滕飞（1984—），女，2011年于法国巴黎中央理工大学获得计算机科学博士学位，现为西南交通大学讲师，主要研究领域为云计算，分布式调度，社区发现等。

LI Tianrui was born in 1969.He received the Ph.D.degree in data mining from Southwest Jiaotong University in 2002.Now he is a professor and Ph.D.supervisor at Southwest Jiaotong University,and the senior member of CCF. His research interests include cloud computing,data mining and artificial intelligence,etc.

李天瑞（1969—），男，福建莆田人，2002年于西南交通大学获得博士学位，现为西南交通大学软件工程系主任、教授、博士生导师，CCF高级会员，主要研究领域为云计算，数据挖掘，人工智能等。发表学术论文150余篇，主持过多项国家科学基金。

Incremental Learning Algorithm of Community Detection under Guidance of Modularity*

WANG Hongjie1,2,TENG Fei1,2+,LI Tianrui1,2
1.School of Information Science and Technology,Southwest Jiaotong University,Chengdu 611756,China
2.Key Lab of Cloud Computing and Intelligent Technology of Sichuan Province,Chengdu 611756,China
+Corresponding author:E-mail:fteng@swjtu.edu.cn

There are many static algorithms in the community detection fields but very few of them are able to fit into the current network circumstances where network sizes are getting larger and small-scale changes are getting more frequent.To deal with the limitation,this paper proposes an incremental learning algorithm of community detection based on modularity,which takes consideration of two basic kinds of community operations,edge changes and point changes,and the incremental learning process is carried out with guidance of the principle of modularity maximization.Experimental evaluation shows that the incremental learning algorithm is capable of partitioning new timely changed nodes into existed communities rapidly without any devastation to primitive divisions.Meanwhile,the result is proved to get close to that gained by static algorithm thus saving time and keeping real-time.

community detection;incremental learning;modularity

10.3778/j.issn.1673-9418.1603045

A

TP311

*The National Natural Science Foundation of China under Grant No.61573292(国家自然科学基金).

Received 2016-02,Accepted 2016-04.

CNKI网络优先出版:2016-04-19,http://www.cnki.net/kcms/detail/11.5602.TP.20160419.1143.004.html

WANG Hongjie,TENG Fei,LI Tianrui.Incremental learning algorithm of community detection under guidance of modularity.Journal of Frontiers of Computer Science and Technology,2017,11(4)：556-564.