二项分布与超几何分布的数学期望研究
北京101中学(100091)
方雯琪●
二项分布与超几何分布的数学期望研究
北京101中学(100091)
方雯琪●
二项分布、超几何分布是比较重要离散型分布,而它们之间不仅有联系,还有存在区别,二项分布与超几何分布的数学期望是反映随机变量的一种非常重要的数字特征.因此,作为学生,我们应熟练掌握二项分布数学期望以及超几何分布数学期望,并将之应用到实际生活中.本文就二项分布与超几何分布的数学期望进行研究.
二项分布;超几何分布;数学期望
在高中数学中,二项分布和超几何分布是两个非常重要的概率模型,这两个概率模型能够解决生活中的许多问题.在离散型随机变量分布中,二项分布、超几何分布是比较重要的分布,二项分布与超几何分布两者之间既存在联系又有所区别.随机变量的数学期望在概率论中占有非常重要的地位,它是反映随机变量的数字特征.因此,对于学习高中数学来说,熟练掌握二项分布、超几何分布的数学期望具有重要的意义.
一、二项分布与超几何分布
1.二项分布


随机变量X记为X~B(n,p),X服从二项分布,即在n为1时,X服从0~1的分布.
2.超几何分布
设某个产品有N件,在这些产品中正品有M件,采取不放回抽样的方式从中抽取n件产品,用Y来表示抽取的产品中正品的个数,则有m件正品的概率为:
随机变量Y记为Y~H(n,M,N),Y服从超几何分布
3.二项分布与超几何分布的关系

超几何分布的极限分布是二项分布,即


二、二项分布与超几何分布的数学期望
1.二项分布的数学期望

(1)定义法求解:

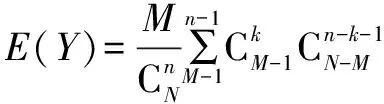
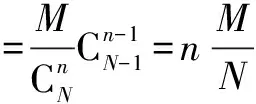
(2)利用性质求解:

2.超几何分布的数学期望
与二项分布的数学期望相比,超几何分布的数学期望也可以应用定义法和利用性质进行求解,但是定义法求解的数学期望比利用性质求解的数学期望更麻烦,然而超几何分布的数学期望与二项分布的数学期望相同.值得一提的是,随机变量和的数学期望与随机变量数学期望的和相等,但是这些随机变量并不一定是相互独立的.
例1 某种产品有80件,在这些产品中次品有8件,采取抽样的方式从中抽取4件产品,计算出在这4件产品中次品数的期望值.
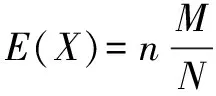
例2 一送客车载了20位乘客,从起点到终点之间有10个车站可以供乘客下车,但只有乘客下车才会在站点停车,乘客不下车就不停车.用X表示停车的次数,求E(X).
解Xi为第i站有人下车,i=1,2,…,10,X=X1+X2+…+X10,则E(X)值为多少.
乘客在第i站不下车的概率为(9/10),那么这20位乘客在第i站不下车的概率为(9/10)20,则乘客在第i站下车的概率为1-(9/10)20.
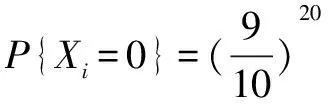


E(X)=E(X1+X2+…+X10)=E(X1)+E(x2)+…+E(X10)=10[1-(9/10)20]=8.8.
上述的求解方法是先将X分解,再利用随机变量和的数学期望与随机变量数学期望之和是相等的来求解,这种方法具有一定的实际意义且在某种程度上可以简化问题.

我们在学习二项分布、超几何分布时,通常会将二者混淆,而且在解决实际问题时,也不知该使用何种分布.然而二项分布数学期望与超几何分布数学期望是相同的,只需稍微修改一下超几何分布模型就可以将之变为二项分布.
[1]吴海军.超几何分布的期望与二项分布的期望相等[J].中学数学教学参考,2015,12:93.
[2]毛晓峰.关于几何分布的数学期望[J].数学教学研究,2015,10:56-57.
[3]黄太纯.二项分布及其应用[J].高中生学习(高二版),2012,12:32-34.
[4]洪奕迅.浅析高中数学中的二项分布与超几何分布[J].新课程学习(中),2013,03:66.
[5]燕建梁.超几何分布及其推广[J].太原师范学院学报(自然科学版),2013,01:21-23,31.
[6]杨华,黄殷.是超几何分布,还是二项分布[J].中小学数学(高中版),2011,Z2:49-51.
[7]翟明娟.概率统计中有关超几何分布的一个误解[J].统计与决策,2014,03:26-28.
[8]余锦银.二项分布的常见题型[J].高中生学习(高二版),2014,01:31-33.
G632
B
1008-0333(2017)07-0010-02

