求一个曲线方程的多种解法
江苏省启东市汇龙中学(226200)
张仁华●
求一个曲线方程的多种解法
江苏省启东市汇龙中学(226200)
张仁华●
本文以一个典型问题为例,从角、斜率、极坐标等五个不同的角度,分析求解曲线方程,运用联系、变化、发展的数学思想方法,分析总结求解曲线的极坐标方程和参数方程的方法.
曲线方程;普通方程;极坐标方程;参数方程
一般地,求解曲线方程的步骤是:
①建立适当的坐标系,设曲线上任一点M的坐标;
②写出适合条件的点M的集合;
③用坐标表示集合,列出方程;
④化简方程为最简形式;
⑤证明所得的方程是曲线的方程.
其中步骤②是个难点,它需要运用数学知识,利用联系、变化、发展的观点,观察并解决这个问题.
题目 过定点A(-2,0),作任意直线交y轴于B点,在直线上取一点P,使|BP|=|OB|,求点P的轨迹方程.
方法一 以角为参数,求出点P的参数方程,再将其化为普通方程.

解 如图,设轨迹上任意一点P(x,y),取∠DAP=θ,θ为参数,过P作PD⊥x轴于点D,过B作BC⊥PD于点C.
在Rt△AOB中,|OB|=|AO|tanθ,则
x=|OD|=|BC|=|BP|cosθ=|OB|cosθ=2tanθcosθ=asinθ.
y=|DP|=|OB|+|CP|=|OB|+|BP|sinθ= 2tanθ(1+sinθ).


因为x+2≠0,所以(x-2)y2+x2(2+x)=0,即x3+xy2+2x2-2y2=0.
所以点P轨迹的普通方程为x3+xy2+2x2-2y2=0.
方法二 以直线AB的斜率k为参数,列出方程,然后消去k,将其化为普通方程.
解 设P(x,y),直线AB的斜率k,则l:y=k(x+2),令x=0,得y=2k,则B(0,2k).
所以BP2=x2+(y-2k)2=OB2=(2k)2,所以x2+y2-4ky=0.

所以点P轨迹的普通方程为x3+xy2+2x2-2y2=0.
方法三 利用直线AB的参数方程,列出点P的参数方程,再将其化为普通方程.
想要灵活运用参数方程解题,首先必须理解参数的几何意义,尤其直线的点角式参数方程中参数的几何意义要深刻理解,否则就不能很好地运用.


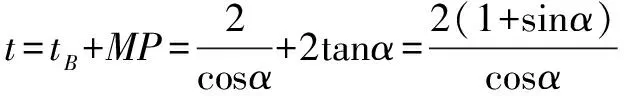

所以ycosα=2(1+sinα)sinα,即y2cos2α=4(1+sinα)2sin2α,

所以点P轨迹的普通方程为x3+xy2+2x2-2y2=0.
方法四 利用曲线的极坐标方程,先求出点P的极坐标方程,再将其化为普通方程.




所以2cos2θ=ρcosθ.
因为ρ=0,满足上式,所以2(x2-y2)=(x2+y2)x,
所以点P轨迹的普通方程为x3+xy2+2x2-2y2=0.
方法五 利用曲线的极坐标方程和三角形面积公式,列出点P的极坐标方程,再将其化为普通方程.


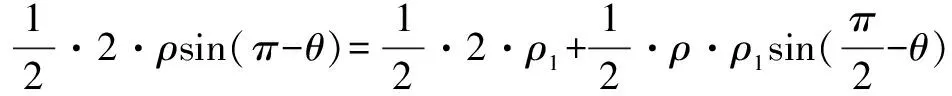

所以4y2=2(x2+y2)+(x2+y2)x,即x3+xy2+2x2-2y2=0.
所以点P轨迹的普通方程为x3+xy2+2x2-2y2=0.
评析 求极坐标方程,有时常用三角形面积列方程,化简求解.
总之,数学中的参数有一种活力,它能分散难点,化难为易,灵活运用参数是解题能力的一种提高,并能从中培养分析问题的能力.
通过上面这个题目的展示,我们可以体会到,对待问题要运用联系、变化、发展的观点分析问题,突破难点,使得思路变得简单统一.我们平时在指导数学学习和数学教学时,若能多分析、解剖数学内容和教学过程,清晰、辩证地讲解数学演绎的逻辑过程,就可以使学生在数学学习中避免失误,少走弯路.只有透彻明了地看待数学问题的思路,才能掌握好数学的思想和精神.
[1]单墫.普通高中课程实验教科书·数学2(必修)[M]. 第4版.南京:江苏教育出版社,2012.
[2]单墫.普通高中课程实验教科书·数学2-1(选修)[M]. 第3版.南京:江苏教育出版社,2012.
[3]单墫.普通高中课程实验教科书·数学4-4(选修)[M]. 第3版.南京:江苏教育出版社,2012.
G632
B
1008-0333(2017)07-0012-02

