细节决定成败——高三数学课堂之我见

安徽省无为县第二中学(238300)

安 英●

细节决定成败
——高三数学课堂之我见

安徽省无为县第二中学(238300)

安 英●

古人说：“行百里者半九十.”最近笔者由于工作关系频频走进一些学校高三课堂，高考专题复习都如火如荼.高三数学进入后期的关键阶段，尽管用时一般不过两三个月，但却是一轮复习的巩固、深化和提高，在一定程度上决定着高考的成败.所听课中有不少设计示例目标定位准确、教学流程清晰、内容可圈可点，让我印象深刻、备受启发；但笔者认为也存在一些问题，在此与各位同仁商榷，供即将走进高三的师生斟酌与思考.

一、 关注细节

细节决定成败.中国有句成语“千里之堤毁于蚁穴”，西方有句谚语“魔鬼在细节中，天使在细节中”， 一个细节的失误往往导致整个解题的失败.这就提醒和启示我们：教师在后期的复习中解题教学不能只重教法，更应在关注细节上给力，解决“会而不对，对而不全”、“会做但算错了”的问题.

本文就课堂上的例题，总结易错的细节问题大致有以下几种：

1.基本概念不清

解题时经常出现的问题是基本概念的理解不够透彻，所以错误百出.

2.基本运算错误

解数学题运算能力尤为重要，一个不起眼的错误细节可能会断了思维的方向，整个问题解决陷入了僵局，导致全盘瘫痪.比如，立体几何题中算错了一个线段的长度，原先运用勾股定理逆定理可推导出的一个直角三角形还原不了，原很容易可以找到的一条垂线找不到了，题目僵住了.学生的运算能力非一日之功，务必养成良好的运算习惯.

3.缺少分类情况

“分类讨论”是学生最易疏忽的一个细节.让学生清楚分类讨论的意义：在解决数学问题时，对于因为存在一些不确定因素无法解答或者结论不能给予统一表述的数学问题，我们往往将问题按某个标准划分为若干类或若干个局部问题来解决，通过正确的分类，能够克服思维的片面性，可以使复杂的问题得到清晰，完整，严密的解答.明白分类讨论的要求：正确应用分类讨论思想，是完整解题的基础.有些问题常常解到某步后，不能再以统一的思维继续下去了，也就是说后面的问题包含多种情况，务必分类讨论，最后把各种情况综合结论.同时应用分类讨论思想解决问题，必须保证分类科学，统一，不重复，不遗漏，在此基础上减少分类，简化分类讨论过程.

例2 过点(1,2)并且在两个坐标轴上的截距相等的直线有几条?

正确解答是一条为：x+y-3=0.另外一条截距为0经常易忘，此时直线过原点，即y=2x(与x轴和y轴的截距都为0).

4.隐含条件缺失

有些题条件不明晰，解题时必须小心挖掘使用这些隐含条件，否则解题就会受阻.

例3 若关于x的方程2cos2(+x)-sinx+a=0 有实根，求实数a的取值范围.

正确解法：原方程变形为：

本题若忽略函数定义域，如: - 1≤sinx≤1 的隐含条件的话，就前功尽弃了．

5.逻辑关系不清

解数学题要合情合理，一步步推导下去． 可学生解题时经常在一步到下一步中间出现可能连自己都觉察不出的漏洞，或者莫名其妙地附加了本来根本没有的条件． 这些都是逻辑关系不清的表现．

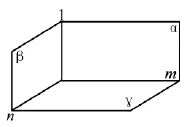
例4 证明: 三个两两垂直的平面的交线两两垂直．

正确解法:

证明设三个两两垂直的平面是α，β，γ，α∩β = l，γ∩β = n，γ ∩α = m． 在平面γ 内任取一点A( 不在l 上即可) ，过A 作AB⊥m于B，过A 作AC⊥n 于C，α⊥γ，所以AB⊥α．

l 在平面α内，所以，l⊥AB． 同理l⊥AC．

又AB，AC 在平面γ 内，且相交于点A，所以，l⊥γ．

因为m ，n 在γ 内，所以l⊥m，l⊥n．

同理可证m⊥n，所以，三个两两垂直的平面的交线两两垂直．

学生总是逻辑关系不清，容易犯用结论证明结论的错误，即先入为主地认为某两条线是垂直的是已知条件，显然在做无用功．

由于数学题千变万化，而学生解题能力千差万别，因而因细节造成的解题错误也就千情万种． 因此，我们要引导每一个学生关注解题细节，努力做到细节问题少惹祸、少犯错，完美解题得高分、拿满分．

G632

B

1008-0333(2017)07-0046-01