外转子永磁高速电机转子振动特性分析

卢南方，雷小叶，杨 立，张 宇

(1.贵州大学，贵阳 550025；2.贵州工业职业技术学院，贵阳 550025；3.贵州凯敏博机电科技有限公司，贵阳 550025)

外转子永磁高速电机转子振动特性分析

卢南方1，雷小叶2，杨 立1，张 宇3

(1.贵州大学，贵阳 550025；2.贵州工业职业技术学院，贵阳 550025；3.贵州凯敏博机电科技有限公司，贵阳 550025)

在外转子高速永磁电机转子设计中，为了提升电机转子高速旋转的稳定性，避免转子高速引起振动和发生扫膛，通过NX软件建立了转子几何模型，导入有限元分析软件进行自由模态分析，获得了电机转子的固有频率与振型图；并进行试验模态分析实测，与前者数据作比较，结果吻合，验证了动力学模型的正确性。通过施加轴承约束求解模态，估算了转子结构的合理转速。

外转子高速电机；振动；模态分析；模态试验

0 引 言

永磁无刷电机根据转子的位置不同，分为内转子与外转子电机。在相同体积和电参数条件下，外转子气隙直径较大，比内转子具有更大的输出扭矩和转动惯量[1]。又因较大的转动惯量，外转子电机飞轮滤波效应更加明显，使其力矩波动更小。根据其特殊结构，负载件可直接设计在转子上，实现与电机的一体化，结构更加紧凑，从而避免更多的机械损耗，降低了生产成本，被广泛应用于各类风机、泵类、机车、航模领域。

外转子电机的优点也是其设计的难点，气隙直径大，导致线速度大；转子结构是悬臂薄膜结构，随着转子工作频率提高，极易产生共振，发生摩碰现象，对轴承产生磨损，影响电机的稳定性，并造成安全隐患[2-3]。对电机转子振动特性分析是继电机电磁设计后的重要环节，是保障电机稳定运行、降低噪声的有效手段。

本文以某型24 V，10 000 r/min外转子高速永磁电机转子样机为例，通过ANSYS Workbench有限元软件对其进行模态分析；利用INV3020型数据采集仪进行数据采集，使用DASP10软件对采集的数据处理，进行试验验证分析, 验证有限元模型的准确性，在此基础上加入轴承约束预估转子稳定转速范围。

1 转子动力学建模及试验验证

对转子采用自由-自由边界条件的自由模态分析，得到的结构振动特性，即转子不受任何外界干扰的固有属性，是最理想也是最容易验证的数学模型。

通用的动力学数学模型：

当转子为自由振动并忽略阻尼，假设材料是线弹性材料，不包含非线性因素时，即[C]=0，F(t)=0，发生谐振动时，位移x=Usin(ωt)时，则方程：

式中：刚度系数矩阵K和质量矩阵M在确定几何尺寸与材料属性时即确定，进而固有频率ωi和振型φi可从上面的矩阵方程式里获得。

1.1 转子有限元模型的建立

外转子高速永磁无刷电机转子为悬臂梁结构，转子机壳卷制成薄壁圆柱状，烧结钕铁硼磁钢粘接在转子轭部内壁，可承受较大的离心力。其结构如图1所示。

图1 电机转子结构NX模型

从式(2)可知固有频率ωi和振型φi由材料的刚度和质量共同决定，在有限元仿真中，由杨氏模量、泊松比和质量密度来确定上述两个矩阵值。材料参数的选择是所建模型的准确性以及模态计算结果误差的主要来源，采用试验模态是检验模型参数选择正确与否的有效手段。通过查阅材料设计手册以及材料供应商提供的资料，所选各部件的材料及相关参数如表1所示。

表1 各部件材料属性

在ANSYS Workbench的模态分析中，系统默认组件间为绑定约束。转子轭部和磁钢几何形状规则，采用六面体划分，转子后盖采用四面体划分，轴采用混合单元划分。建立出来的有限元模型如图2所示，共202 645个节点，32 742个单元组成。

图2 转子有限元模型

1.2 自由模态分析

对转子进行12阶模态分析，分析表明前6阶固有频率接近零，振型在6个自由度窜动，为刚性模态，后6阶发生明显变形为振动模态。图3为提取的转子后6阶振动模态固有频率和振型。

由图3可知，1阶固有频率与2阶固有频率值极为相近，振型虽然未发生在同一个平面，但最大位置均发生在轴输出端，最小位置在转子轭部。3阶、4阶振型出现在转子轭部一端，开始出现薄膜模态。5阶、6阶最大振型发生在磁钢位置，并且固有频率两两相近。分析表明外转子结构除具备轴对称转子在模态分析中特征方程会出现重根现象外，在二阶振动模态后还会出现薄膜模态。得出的结论与文献[4]、文献[5]研究相符。

(a)1阶振型(955.6Hz)(b)2阶振型(956.7Hz)(c)3阶振型(1935.4Hz)(d)4阶振型(1939.3Hz)(e)5阶振型(4361.3Hz)(f)6阶振型(4364.9Hz)

图3 自由模态频率及振型云图

1.3 试验验证

为获得电机转子的实际振动特性来验证有限元动力学模型的正确性，采用INV3020型数据采集仪对样机进行转子在自由-自由状态下的模态敲击试验。自由-自由状态用橡胶绳悬吊模拟，试验现场如图4所示，试验装置由INV3020型数据采集仪、激励锤、加速度传感器、电机转子以及计算机组成。

图4 转子模态测试装置

图5显示试敲的能量激励为5 kHz,在确保力信号采样点数不少于20个同时，满足采样定理，采用频率定在20 kHz，变时倍数设为2。

激励锤沿转子轭部圆周敲击18个点,分3排，每排6个点，得到转子的各测点每阶固有频率和振型。图6为第1测取点频响函数幅值及相干图。

将采集到的数据导入模态分析模块,基于频响函数的基础上，通过时域法求解脉冲响应函数,然后采用特征系统实现算法(ERA)对18个测试点模态拟合[6]。根据稳态判定准则MAC在特征矩阵中判定模态值，生成了转子的试验固有频率和模态振型云图，如图7所示。

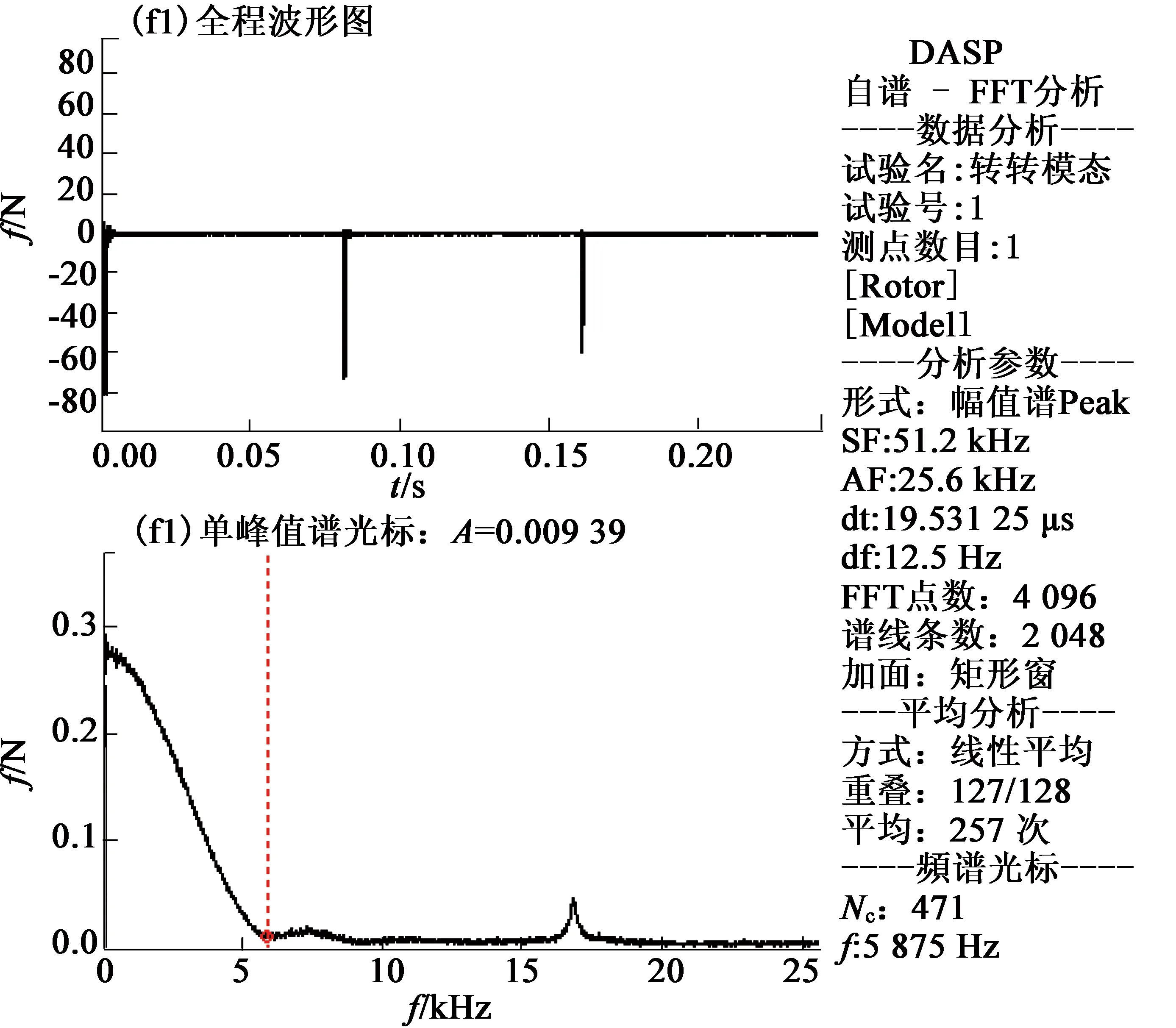
图5 力频信号自谱分析

图6 频响函数幅值及相干图

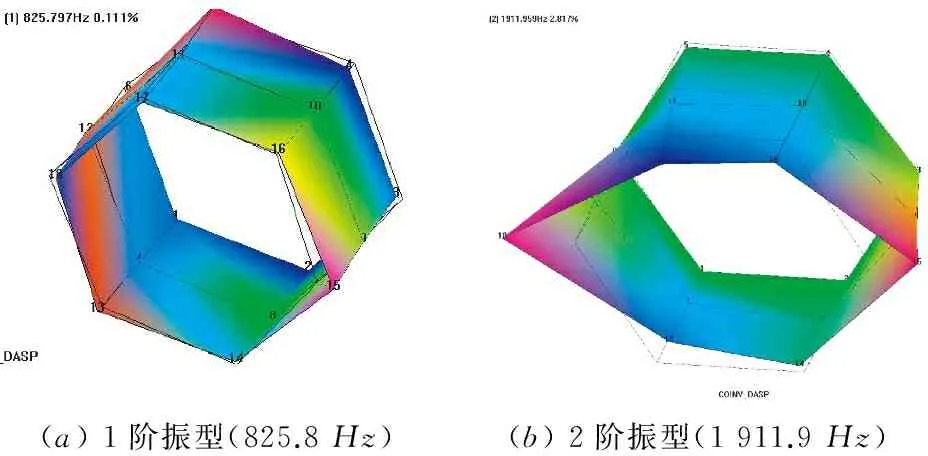
(a)1阶振型(825.8Hz)(b)2阶振型(1911.9Hz)

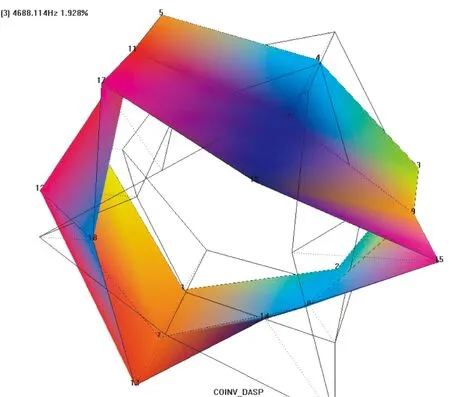
(c) 3阶振型(4 688.1 Hz)

试验模态振型的拟合为转子轭部18个点，转子轴因为体积过小，并未直接测取，在试验中1,2阶振型带来了较大的误差。比较图3、图7，在表2中列出了仿真与试验对比；由于模态出现重根，在试验中得到的振型两两重合，振型轨迹与仿真一致，试验数据和仿真基本吻合，验证了动力学模型的正确性。

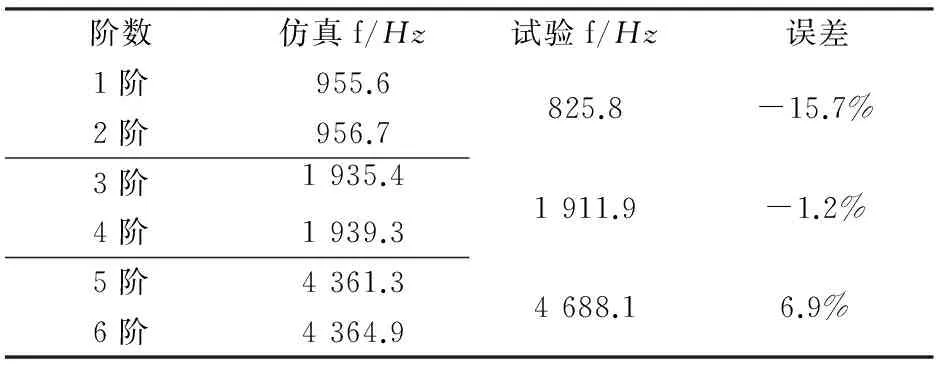
表2 计算模态与试验模态对比

2 约束模态分析

微特电机使用的轴承一般为高速滚动轴承，它的刚度系数为2×107～1×109N·m,阻尼很小，通常忽略不计[7]。固有频率随刚度的提高而增加，在轴肩位置施加轴承约束，取最小刚度系数模拟电机转子实际支撑情况，可得最低情况的振动特性。模型加入远端位移约束，约束轴向攒动与旋转，求取其前12阶模态，仿真结果如图8所示。

(a)1阶振型(0.03Hz)(b)2阶振型(310.0Hz)(c)3阶振型(616.0Hz)(d)4阶振型(619.5Hz)(e)5阶振型(1354.6Hz)(f)6阶振型(1355.1Hz)(g)7阶振型(1935.5Hz)(h)8阶振型(1939.3Hz)(i)9阶振型(3614.5Hz)(j)10阶振型(3614.8Hz)

(k)11阶振型(4361.3Hz)(l)12阶振型(4365Hz)

图8 约束模态频率及振型云图

对比图3与图8，加入约束后，固有频率降低，多出多个模态，该电机转子振型频率最小值相差3倍；图8(g)、图8(h)、图8(k)和图8(i)中的振型、固有频率与图3自由模态分析一致，可知加入轴承约束后薄膜模态并未消失。最小固有频率值为310Hz，在不考虑陀螺效应下对应一阶转速是18 600r/min，分析表明24V下电机单机工作运行不会发生共振，为刚性转子。

3 结 语

本文为外转子永磁高速电机转子设计提供了设计数据与流程参考，在工程生产中具有一定的借鉴意义，得出结论如下：

1)通过有限元分析软件ANSYSWorkbench对外转子永磁高速电机转子进行了自由模态分析，得到了模态特征与振动特性，并用试验模态进行了验证，得到了准确的动力学模型，可用于外转子振动特性研究。

2)计入最小刚度轴承约束对电机转子进行了模态分析，对两种边界条件的模态特征进行了对比，该结构约束下模态与自由模态振动频率最小值相差3倍，设计中应不小于这个倍数，可作为同类电机设计参考。

[1] 刘刚,张卫，陈强.基于ANSYS的航空电机转子振动分析[J].微特电机,2014,42(4):47-48.

[2] 王天煜,王凤翔，方程.高速电机转子临界转速计算与振动模态分析[J].辽宁工程技术大学学报:(自然科学版)2009,28(5):805-808.

[3] 谭建成.永磁无刷直流电机技术[M].北京:机械工业出版社,2011.

[4] 臧朝平,刘银超.轴对称结构的模态振型描述和模态确认[J].南京航空航天大学学报,2012，44(5):725-733.

[5] 董奇,郑津洋，胡八一.壳体中的轴对称模态和非轴对称模态[C]//压力容器——第七届全国压力容器学术会议论文集.北京：化学工业出版社，2009：459-461.

[6] 王正.转动机械的旋转子动力学设计[M].北京:清华大学出版社,2011.

[7] 催定宇,辛克贵,祁泉泉.扩展特征系统实现算法的模态参数识别特性研究[J].工程力学,2013，30(8):49-53.

Vibration Characteristics Analysis Rotor of Outer Rotor Permanent Magnet High-Speed Motors

LUNan-fang1,LEIXiao-ye2,YANGLi1,ZHANGYu3

(1.Guizhou University,Guiyang 550025,China;2.Guizhou Industry Polytechnic College,Guiyang 550025,China;3.Guizhou Creator Electronic Technology Co., Ltd.,Guiyang 550025,China)

In order to improve the rotating stability of motor rotor, avoid vibration and the rotor touch stator caused by high rotation of the rotor on the design of rotor in Outer rotor permanent magnet high-speed motor, professional dynamic finite element analysis software was used to solved simulation mode followed by the geometric model of the rotor established by NX software. The natural frequencies and mode shapes map of motor rotor were obtained, and it is found that numerical simulation is consistent with those datum that measured by modal analysis testing. The dynamic model was validated.By imposing bearing constraint to solve the model, the reasonable speed of rotor structure was estimated.

out rotor high-speed motor; vibration; modal analysis; modal testing

2016-10-11

贵州省科学技术基金项目(黔科合LH字[2014]7399)；贵州省科技合作计划项目(黔科合LH字[2015]7177)；面向智能领域的"技术众筹"研究生创新基地项目(贵大研CXJD[2015]003)

TM351

A

1004-7018(2017)03-0020-03

卢南方(1991-)，男，硕士研究生，研究方向为微特电机设计及其转子动力学。