汽车发电机定子建模及结构优化

贺岩松，张 浩，张全周

(1.机械传动国家重点实验室(重庆大学)，重庆 400044； 2.重庆大学，重庆 400044)

汽车发电机定子建模及结构优化

贺岩松1,2，张 浩2，张全周2

(1.机械传动国家重点实验室(重庆大学)，重庆 400044； 2.重庆大学，重庆 400044)

通过振动噪声台架测试，发现发电机在中低转速下的36阶次电磁噪声问题突出。因此，定子结构的准确建模及结构优化是电磁振动噪声分析和控制的基础。首先对汽车发电机的定子进行自由模态试验，得到模态参数。建立定子冲片的整体式铁心模型后，采用等效法对线圈进行简化并建立4组定子模型。利用ANSYS软件对所建立的模型进行模态仿真，对比试验结果确定了定子的建模方法。模态结果和噪声试验显示，36阶次电磁噪声是由定子的共振导致。对定子铁心模型进行结构优化，结果表明，定子的模态特性得到了有效的改善。

发电机定子；模态分析；模态试验；结构优化

0 引 言

汽车交流发电机的振动噪声严重影响整车的NVH性能，是各汽车厂家的研究热点。汽车交流发电机振动噪声主要包括机械振动噪声、电磁振动噪声、空气振动噪声三大类[1]。

对于机械振动噪声，目前都能通过精度和工艺的控制解决，且机械振动噪声所占比例很小[2]。空气振动噪声在采用不等节距叶片结构等措施得到有效控制[3]。电磁噪声是电磁径向力波与定子固有频率接近时，引起共振，使振动噪声增强[4]。定子的结构模态研究是电磁振动噪声控制的重要研究方向。

在对发电机定子结构研究时，定子的建模是结构分析前提和难点。针对上述问题，目前主要采用将硅钢片叠加的铁心和铜线缠绕的线圈进行简化处理。文献[5]在研究电机模态时将定子绕组等效为空心圆柱体,密度则按绕线与气隙的比例来确定，其有限元分析结果与敲击实验结果吻合较好。文献[6]在研究电动机定子模态时，利用ANSYS较准确地计算了定子的模态振型和固有频率。文献[7]采用多种有限元模型研究了异步电机定子的固有模态，并与试验结果做了比较，得到比较好的简化模型。文献[8]分析了绕组对电机定子冲片模态的影响。但是，对于汽车发电机定子的建模和结构优化设计的研究很少。

本文通过发电机振动噪声台架试验发现定子的共振产生了较大的峰值噪声，定子的建模和结构优化成了亟待解决的问题。针对对发电机定子结构的建模难点，利用等效法建立定子简化模型。对模态仿真和模态试验结果进行对比，验证了建模的准确性和可靠性。对定子进行了结构分析和优化设计，有效地提升了模态特性，为发电机的电磁振动噪声分析奠定了良好的基础。

1 发电机振动噪声试验

1.1 发电机振动噪声台架测试

发电机振动噪声台架试验在某知名汽车公司的发电机噪声测试实验室(按照国家标准搭建)完成[9]。该实验室主要包括半消声室、发电机驱动试验台、噪声数据采集分析系统。试验时，如图1所示，在发电机前、后、左、右和上方5个距发电机中心均为0.5 m处来布置传声器。

图1 汽车发电机噪声试验台架

目前汽车车发电机台架试验包含空载工况与负载工况，采用升速法测试发电机在两种工况下时2 000～15 000 r/min范围内的噪声数据。

1.2 发电机噪声结果分析

对试验数据进行处理可以得到该型发电机在空载工况和负载工况下的噪声声功率级-转速曲线，如图2所示(A计权网络下)。

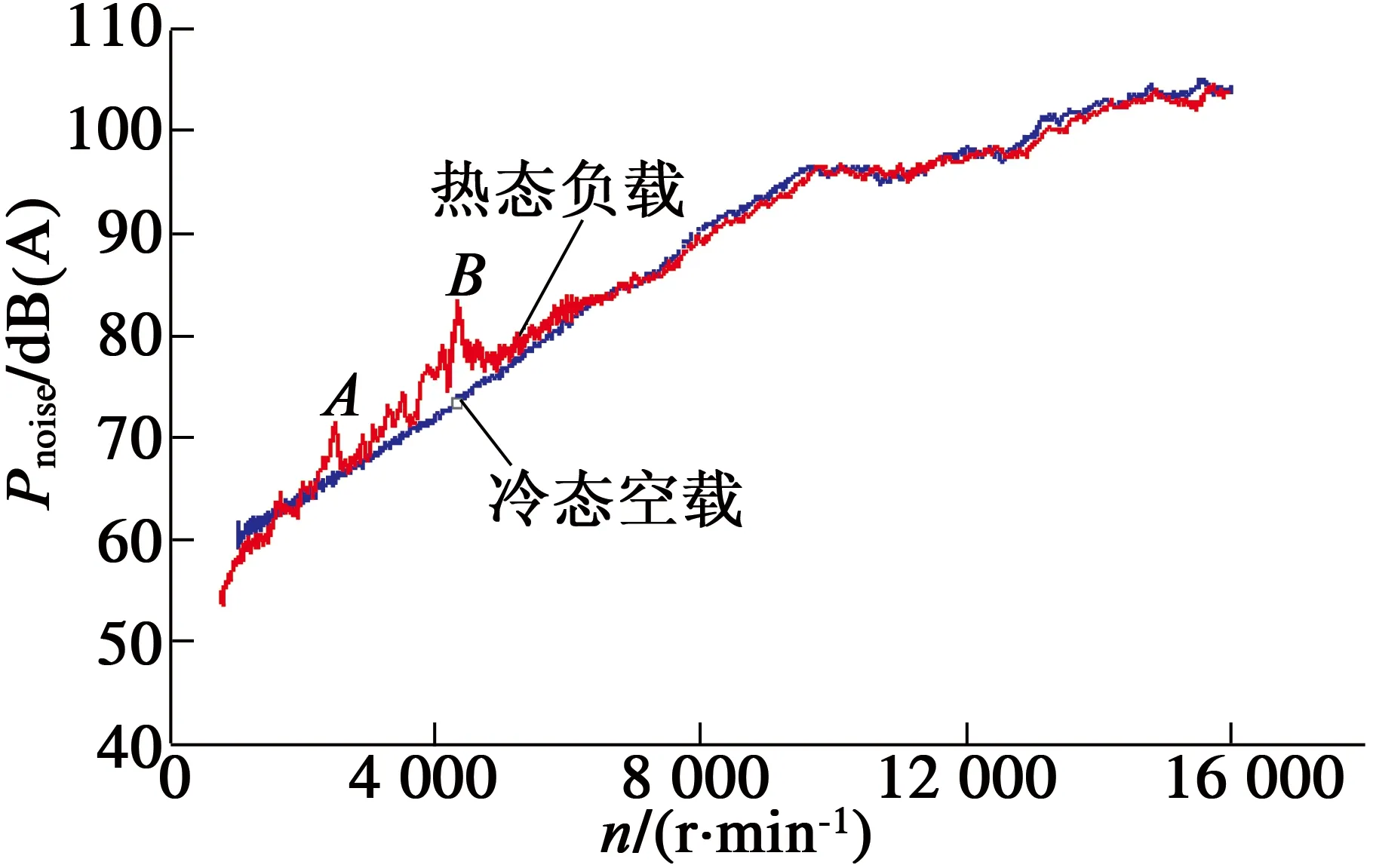
图2 空载和负载工况下的噪声声功率级-转速曲线

试验结果表明，两种工况下发电噪声声功率级均随转速增加而上升，但在中低转速(2 000～4 500 r/min)范围内，同转速下负载工况的声功率级高于空载工况的声功率，说明电磁噪声是中低转速下的主要成分。负载工况下，2 500 r/min(A点)和4 350 r/min(B点)处出现了两个明显的峰值，声功率级也达到了71.8 dB和83.5 dB。中低转速范围内，定子振动产生的电磁噪声严重影响发电机的NVH性能。

阶次分析可用于分析转速不稳定的旋转机械以避免频谱上的“频率混叠”[10]。对中低转速段(2 000～4 500 r/min)负载工况下的发电机噪声数据进行阶次分析，如图3所示。

汽车发电机的电磁噪声的频率可表示：

式中：i为谐波次数；n为转速。

在中低转速范围内，36阶次噪声为该发电机电磁噪声的主要成分。电磁噪声主要是定子振动所产生的，因此定子结构研究是电磁噪声控制的重点方向。

图3 发电机中低转速的噪声频谱图(截图)

2 发电机定子模态试验

试验时，采用足够软和长的绳(固有频率足够低)悬挂被测零部件来尽可能地模拟定子的自由状态。发电机定子悬挂图如图4所示。

图4 定子模态试验悬挂图

在定子上选取18个测点来模拟定子轮廓。采用力锤和加速度计来采集激励力信号和加速度信号，并进行频响函数估计,就可得到固有频率。计算机和LMS数据采集器如图5所示。

图5 计算机和数据采集器

在采用锤击法模态试验过程中，按照固定传感器和移动力锤的方式进行，依次敲击每个测试点，每个测点敲击3次进行平均，以减少随机误差[11]。试验利用LMS模态分析模块对试验数据进行处理后得到模态结果。定子的模态试验频率如表1所示，只分析3 000 Hz以内。定子的第一阶、二阶和三阶振型分别是椭圆、三角形和四边形振型。

表1 定子自由模态试验结果

3 发电机定子自由模态仿真

3.1 模态分析理论

模态分析是用来计算结构振动特性(一般是固有频率和振型)。无阻尼模态分析，具有n自由度的无阻尼振动系统的振动微分方程[12]：

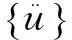
自由振动时，即f(t)=0时，有方程：

式(2)的解：

将式(3)左乘{φ}T得到：

3.2 发电机定子建模

汽车发电机定子是由硅钢片叠加的铁心和铜线缠绕的绕组组成，如图4所示。

建立准确的定子模型是定子结构分析的难点。考虑到铁心的结构形式，建模若采用多层模型叠加结构显得太过复杂。文献[5]和文献[6]验证了采用整体式模型来代替叠压式模型是可行的。因此，本文也采用整体式铁心模型。绕组在结构上具有很大的不规则性，难以按照实际结构来建模，可采用等效法来简化模型。文献[13]采用空心圆柱体来等效线圈时，需要结合模态试验与仿真计算来确定等效后的密度、弹性模量和泊松比,此过程在材料参数确定时有一定盲目性。为此，本文在直接使用设计时所用材料参数的基础上进行建模，建立的36槽铁心模型如图6所示。

图6 发电机定子铁心模型

线圈建模根据的铜线缠绕后的主体轮廓进行简化。在ANSYS中计算时，铁心和线圈为bond接触，因此线圈和铁心的接触面积需合理控制来保证模型的刚度和实际接近。本文根据线圈结构设置了4组对比模型，如图7所示。

图7 4种定子简化模型

3.3 发电机定子模态仿真

定子铁心的弹性模量和泊松比分别为1.95×1011Pa和0.26，线圈的弹性模量和泊松比分别为1.5×1010Pa和0.32。铁心和线圈的网格大小设置均为2 mm。在ANSYS中计算完成后，定子的四种模型的自由模态仿真频率表2所示。

表2 四种定子模型模态仿真频率

四种定子模型的的前三阶模态振型均为椭圆振型、三角形阵型和四边形振型，如图8所示。

图8 四种模型的模态振型图

4种定子模型的前三阶频率偏差(按Δ=[(f仿真-f试验)/f试验]×100%)计算如表3所示。

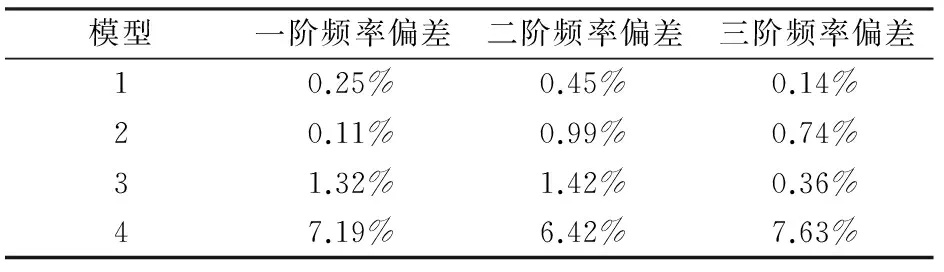
表3 模态仿真频率和试验频率偏差

结果显示，模型4的偏差超过5%，模型3前一、二阶频率的偏差较模型1和2差，效果均不好。虽模型1在一阶的偏差大于模型2，但在二、三阶频率时偏差明显小于模型2，且一阶频率偏差非常小，能较好地满足工程要求。因此，采用模型1的建模方法来建立定子模型是可行的。

按式(1)计算的峰值A,B处的36阶次噪声频率与定子的二、三阶频率如表4所示，两者非常接近，说明定子在1 500 Hz和2 610 Hz附近产生了共振，从而辐射了较大的电磁噪声。定子结构优化是发电机电磁噪声控制的重点研究方向。

表4 定子模态试验结果

4 发电机定子结构优化设计

发电机电磁振动噪声主要来源于定子固有频率和电磁力频率接近时的共振，因此定子结构优化设计使固有频率提升具有重要意义。线圈的结构和功能使得线圈改动难以实施，故可从铁心结构来进行优化。本文从增加定子铁心刚度的角度来进行优化，综合考虑电磁性能、加工制造等因素后，优化设计了如图9所示的铁心结构。

图9 改进后的定子铁心模型

将改进前后的铁心模型分别进行自由模态仿真计算，得到模态频率结果如表5所示。

表5 改进前后铁心模型模态频率

改进后定子铁心的频率提升较多，对于避免发电机定子的共振具有较好的效果。改进前后的铁心的模态振型如图10所示，二者无差别。

图10 改进前后铁心模态振型

加入线圈模型，对改进后的定子进行模态仿真计算(材料参数不变)。改进前后的定子固有频率如表6所示，模态频率有较好的提升效果。

表6 改进前后定子模态仿真频率

改进后的定子振型图如图11所示，与改进前的模态振型基本一致。改进后的定子在频率上提升明显，对避开定子共振，降低振动噪声具有重要意义。

图11 改进后定子的模态振型

5 结 语

本文通过发电机振动噪声试验，发现电磁振动噪声是中低转速下的主要成分。建立了4种定子等效模型。结合模态试验和模态仿真确定了最吻合实际的模型，确定了定子模型的建立方法，为电机的结构优化分析提供了基础。

模态试验和仿真显示，定子在固有频率附近发生共振，进而辐射出较大的36阶次电磁噪声。对铁心模型进行结构优化，定子的模态频率得到了明显提高，对避免定子共振有一定效果。由于条件限制，本文未能完成改进后的噪声测试。发电机定子的建模和结构优化对电磁振动噪声分析和控制奠定基础，具有有一定的参考价值。

[1] 舒波夫.电动机的噪声和振动[M].沈官秋,译.北京:机械工业出版社, 1980.

[2] 宋志环．永磁同步电动机电磁振动噪声源识别技术的研究[D].沈阳:沈阳工业大学,2010.

[3] 陈昕,王朝建,王海洋等．汽车发电机通风声噪阶次分析方法研究[J]．微特电机, 2013，41(10)：37-39.

[4] SENOUS M,LARSEN P,DING Peiran．Electromagnetics, structural harmonics and acoustics coupled simulation on the stator of an electric motor[J]．SAE International Journal of Passenger Cars-Merchanical Systems,2014,7(2):822-828.

[5] 代颖, 崔淑梅, 宋立伟.车用电机的有限元模态分析[J].中国电机工程学报,2011,31(9):100-104.

[6] 潘博, 孙京, 娄丽芬. 电机传动机构动力学建模、仿真与实验验证[J].振动与冲击, 2011, 30(5)：236-240.

[7] 何鹄环.永磁有刷直流电动机电磁振动与噪声的分析[D].上海:上海交通大学, 2012.

[8] 哈鲍晓华, 刘健, 倪有源等．汽车爪极发电机定子模态分析和固有频率计算[J]．汽车工程, 2011.33(12)：1088-1091.

[9] 辛阳,董大伟,闫兵,等．汽车用发电机NVH性能测试声学实验室设计及鉴定[J]．噪声与振动控制,2012,32(3):147-151.

[10] 汪伟, 杨通强．非稳态信号计算阶次分析中的重采样率研究[J]．振动、测试与诊断, 2009,29(3)：349-351.

[11] 梁君,赵登峰.模态分析方法综述[J].现代制造工程, 2006(8)：139-141.

[12] 李晓华. 基于锤击法的车用永磁同步电机的固有频率分析[J].上海电力学院学报，2013，29(5)：421-424.

[13] 单鹏, 马龙. 爪极发电机电磁力及定子振动特性分析[J].微电机，2014，47(3)：33-36.

Modeling and Structure Optimization of Vehicle Alternator Stator

HEYan-song1,2，ZHANGHao2，ZHANGQuan-zhou2

(1.State Key Laboratory of Mechanical Transmission(Chongqing University), Chongqing 400030,China;2.Chongqing University, Chongqing 400030,China)

Vibration and noise test was done in specifically designed lab，which shows 36 order electromagnetic noise is a significant component of the noise of vehicle generator at middle and low speed. While an accurate simulation model and modals is the prerequisite for electromagnetics, structural harmonics and acoustics coupled simulation. Modal characteristics was obtained from modal test based on a type of a stator of vehicle generator. the stator core structure were established according to size of stator punching sheet，and established four simplified models according to the structure of coils and stator core. The computational results by means of the finite element software ANSYS were compared with the experimental results，then the most realistic model was selected. The 36 order electromagnetic noise comes from stator vibration according to results of experiment and simulation.Structure optimization was completed and the results show the stator's modal characteristics were effectively improved.

generator stator; modal analysis; modal test; structure optimization

2016-02-19

重庆市基础与前沿计划项目(CSTC2015jcyjBX0075)

TM34

A

1004-7018(2017)03-0013-04

贺岩松(1968-)，男，工学博士，教授，主要从事车辆系统动力学与控制、噪声与振动控制、智能材料本构关系等方面的教学与研究工作。