思考有根据过程有条理
——以“小树有多少棵”口算教学为例
◇叶 丹 吴剑利
“小数有多少棵”是北师大版教材三年级上册第四单元“乘与除”的第一课时,主要学习整十、整百、整千数乘一位数的口算乘法。在日常教学中,部分教师认为这一内容学生都会了,还需要留出时间让学生探索吗?为了更好地了解学生的学习起点,我们选取三年级中的90名学生进行学情前测。题目如下:
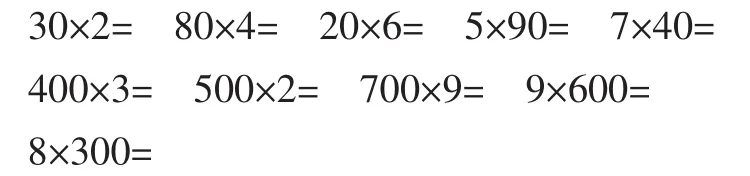
情况统计如下表所示:
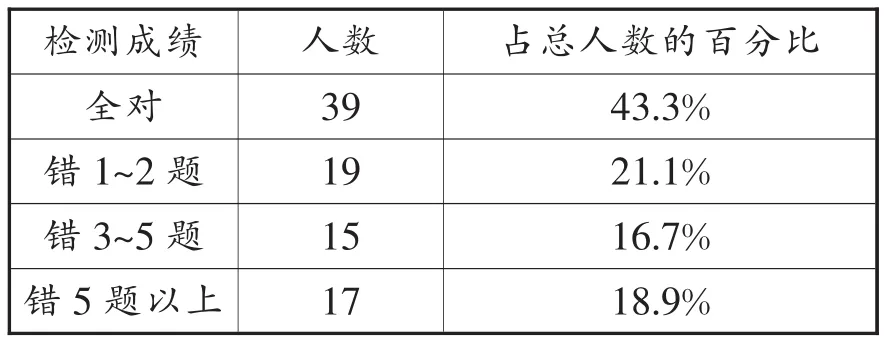
错误归因如下表所示:
我们又随机访谈了10名学生:说说30×2是怎么算的。有8名学生是利用乘法口诀算出得数,然后添0;2名学生利用乘法的意义,两个30就是60。基于以上调查,我们思考:
1.对于整十、整百数乘一位数的口算,虽然部分学生有一定的基础,但缺乏理性认识,因此,从学生的现实起点出发,把算法和算理更好地结合是本节课的教学重点。
2.学生大多数用“先乘后添0”的方法进行计算,教学中要让学生理解这样做的道理,使其“知其然,并知其所以然”。
为了落实上述教学思想,我们沿着学生思维发展的路径,在教学实践中采取了以下递进教学策略。
一、直观比较, 让算理明晰起来
1.依托直观,感悟算法算理。
首先,我们出示情境时,隐去“每车装500棵”的条件,先解决3捆有多少棵,并用旁白的方式提出:6捆一共有多少棵?9捆呢?(如图1)
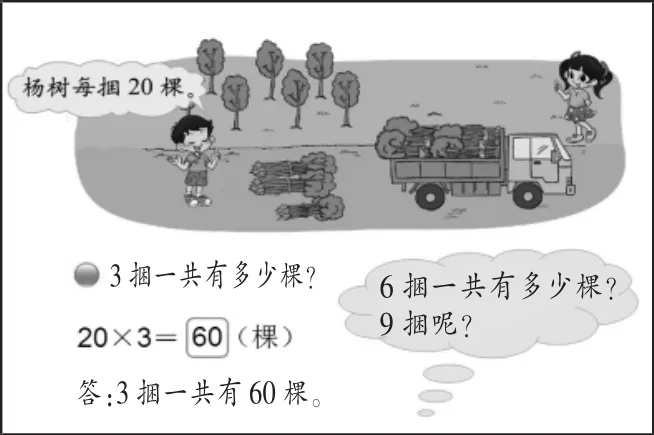
图1
在计算3捆有多少棵时,学生有以下几种方法:(如图2)
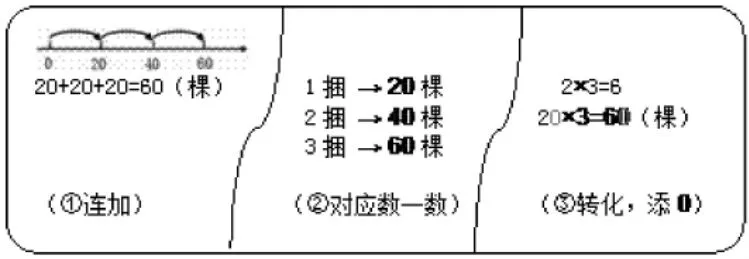
图2
三种算法,体现了学生的不同思维。其中方法③是最简洁实用的:2个一×3=6个一,2个十×3=6个十,只是算清楚几个计数单位就行了。把新知转化为旧知,由表内乘法计算迁移到整十数乘一位数,算法不变,只是计数单位改变。
为了让学生达成算法的自然优化,对教材问题串中的第一个问题进行了追问:6捆呢?9捆呢?使学生感受到优化的必要,选择用表内乘法算出一共有几个计数单位。运算也是一种逻辑推理,由几个一推算到几个十,把运算程序的教学提升到算理的高度。接着,我们将第二个问题中的数据500改成了400(如图3),这样做将每车装500棵改成400棵,是基于帮助学生更好理解算理的设计,能更直观地在计数器上感受数的位值。4个十×2=8个十,在 8后面添一个 0; 4个百×2=8个百,在 8后面添两个0。
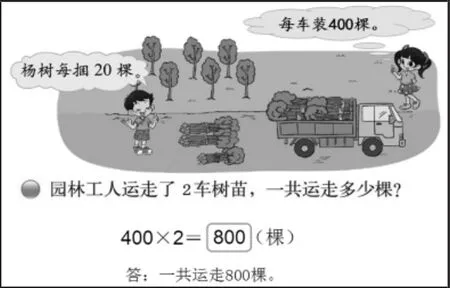
图3
利用计数器(如图4)清楚直观地解释了学生口中“添几个0”的道理,从算法的自然生成中厘清算理的意义,有效促进学生“动作思维—形象思维—抽象思维”的发展。
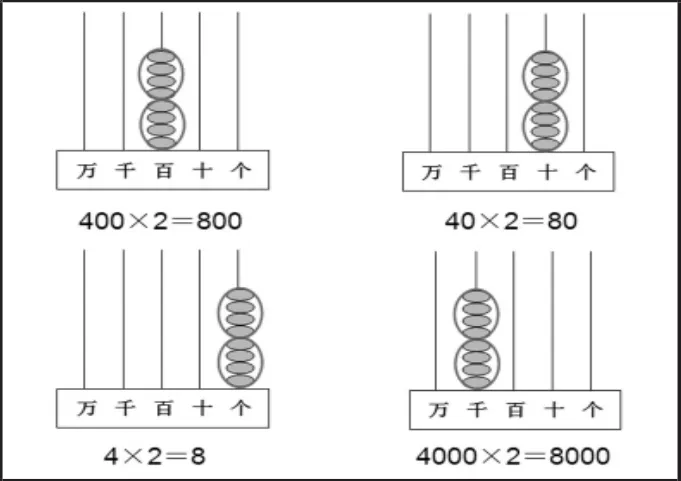
图4
2.迁移比较,明辨算法算理。
观察这一组算式,你能发现什么规律?你还能写出一组这样的算式吗?(如图5)

图5
通过计算、观察每组数据蕴含的规律,进一步理解和掌握乘法口算的计算方法。在计算、观察、交流、实践这一系列活动的过程中,学生能有效地锻炼数学观察力,提高思维的条理性。根据发现的规律,再写一组类似的算式,有助于学生进一步加深对规律的体会和对计算方法的掌握。乘数是整百、整千数的口算方法,学生完全可以从乘数是整十数的口算方法中进行迁移,从而,知识的迁移转化为技能,从感性认识上升到理性认识。
二、 练中求联, 让算法灵活起来
如果学生基本会算,课堂上除保底的练习外,还需要设计不同难度的分层练习,以便深刻理解算理,灵活运用算法。
如,在完成“练一练”第 1题(如图6)的基本要求外,我们追问:40×5=200,4的后面有一个0,为什么答案后面有两个0?进一步明白添0背后数学的意义。
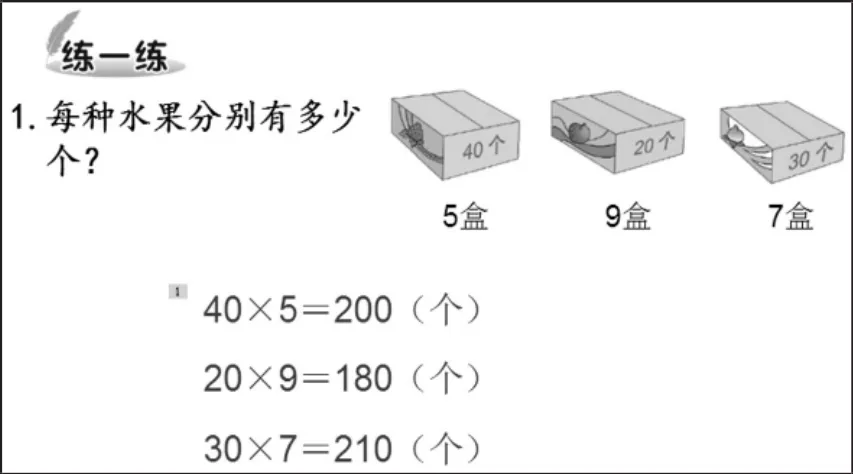
图6
再如,以下的拓展练习(如图7)可以较好地培养学生的估算能力,以及灵活运用所学知识解决实际问题的能力。

图7

