“分数的意义”教学实录
◇张齐华
一、认识单位“1”,建立关系
师:这儿有一些正方形(屏幕显示6个同样的小正方形),你觉得这些正方形可以用什么数来表示?有不同的答案吗?
生:我觉得这些正方形可以用6来表示。
师:猜猜看,他把谁看作了“1”?
生:他把1个正方形看作了“1”。
生:我觉得这些正方形还可以用3来表示,只要我们把2个正方形看作“1”。
生:我觉得这些正方形还可以用2或1来表示。把3个正方形看作“1”,这些正方形就可以用2表示;把6个正方形看用1表示,这些正方形就可以用1表示。
生:我觉得这些正方形还可以用12来表示,如果我们把半个正方形看作“1”。
生:我觉得这些正方形还可以用1.5来表示,如果我们把4个正方形看作“1”。
生:我觉得这些正方形可以用任何数来表示,关键看我们把多少个正方形看作了“1”。“1”变了,这些正方形表示的数也就变了。
(结合学生的发言,教师相应地圈出6个正方形中的“1”,并标出对应的数)
师:的确,“1”是我们计数的基本单位。只有确定了“1”,我们才能够准确地对这些正方形或其他任何东西进行计数。所以,数学上,我们把这里的“1”看作计数的单位,也叫单位“1”。想一想,当我们对这些正方形用6表示时,其实,我们是把几个正方形看作了单位“1”?
生:1个。
师:把1个正方形看作单位“1”,2个这样的正方形,就可以用哪个数来表示?(如图1)

图1
生:可以用2来表示。
师:3个、5个、8个这样的正方形,又可以用哪些数来表示呢?
生:可以用 3、5、8 来表示。
师:你有什么发现?
生:我发现,有几个单位“1”,我们就可以用几来表示。
师:数学上,整数就是单位“1”的叠加,有几个单位“1”,就可以用整数几来表示。如果不满1个单位“1”,或者比几个单位“1”还多一小部分时,我们又该用怎样的数来表示呢?
生:我觉得可以用分数来表示。
生:我觉得还可以用小数来表示。
师:是的,有时候,正因为我们的计数对象不是完整的单位“1”了,所以,我们才创造出了分数和小数。以图2为例,如果把整个圆看作单位“1”,你觉得涂色部分可以用怎样的数来表示?为什么?
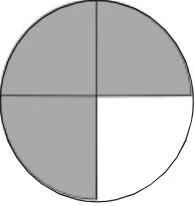
图2
师:整数是单位“1”的叠加,分数则源自对单位“1”的等分。这样看来,整数也好,分数也好,其实都和谁有关?
生:都和单位“1”有关。
师:是单位“1”把整数和分数联系在了一起,单位“1”是整数和分数之间的桥梁!
(结合学生发言,教师相机板书如下)
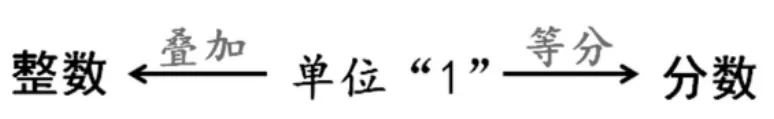
二、丰富单位“1”,深化认识
(学生组内交流,随后全班汇报。学生代表性作品如图3)
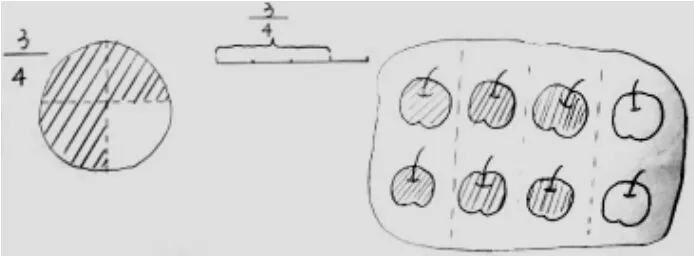
图3
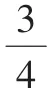
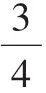
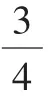
生:因为它们都是把单位“1”平均分成了4份,表示了其中的3份。
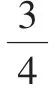
(结合学生的发言,教师相机板书如下)

三、从关系到“数”,拓展理解
师:其实,分数除了可以表示部分与整体的关系,它本身还能表示一个具体的数。比如,(指图3)这是1块饼,那么,涂色的部分是多少块饼?
师:如果这是1米、1盘苹果,那么涂色部分又是多少米、多少盘苹果?
(学生尝试,并在小组内交流想法。随后全班展示)
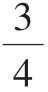
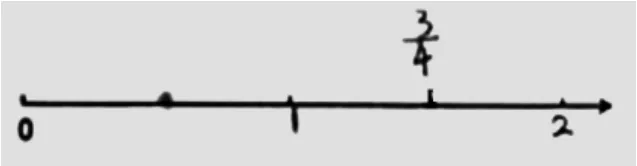
图4
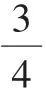
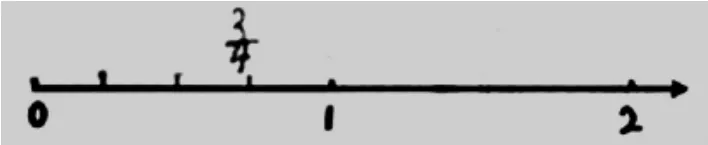
图5
师:比较一下,发现了什么?
生:我发现,第一位同学是把0到2这一段看作单位“1”,而第二位同学是把0到1这一段看作单位“1”。
生:我觉得两位同学都对。因为我们刚才在讨论正方形时就说过,随便几个正方形都可以看作单位“1”。
师:有什么问题或困惑吗?
生:我有个问题。我们都知道,数轴是可以无限延伸的。如果这两个都对,那么,万一数轴很长,这道题的答案就有无数个,那就没意义了。
生:我赞成。如果两个答案都对,那么,我们就没办法在数轴上找到分数的准确位置了。
生:我觉得,这里,我们只能把0到1这一段看作单位“1”。不过……

生:我觉得这个点应该是1.5。
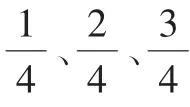

图6
师:有什么发现?又有什么问题?

生:我反对!我觉得只能从左往右数,因为我们的整数就是从左往右数的。
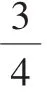
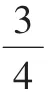
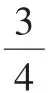
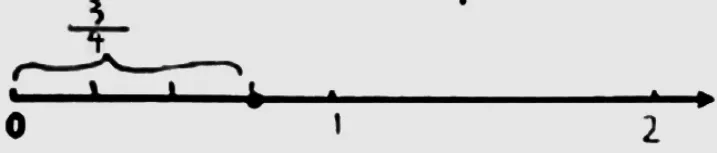
图7
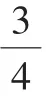
生:我觉得对是对,但有点别扭。因为数轴上,我们都是用点来表示数的,而他是用这一段来表示数的,我觉得不统一。
生:我也觉得有点别扭。如果数轴上的分数都用这样的段来表示,那么,要表示好几个分数时,数轴上就有点乱了。
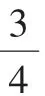
师:看来,和整数一样,分数的确也能够在数轴上找到它们的位置。比较一下这3个分数,你有什么发现?
生:我发现,它们的分母都是4。
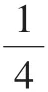

图8
四、由模仿到建构,自我完善
师:学习数学就像我们认识一个人一样,我们需要从不同的侧面去了解它、发现它,这样,我们的认识才会更全面、更丰富。不过,在这些不同的表示方法之间,你能找到它们的联系吗?任意选择两种方式,试着比一比、说一说。
生:我想说画图和文字这两种。我觉得,无论是长方形、线段还是8个苹果,都可以看作单位“1”。这几幅图其实都是把单位“1”平均分成4份,表示了这样的3份。所以,我觉得文字其实就是图的一种浓缩。
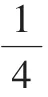


……
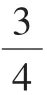
(学生任选一个分数,尝试着用不同方法表示对它的理解。随后,全班交流)
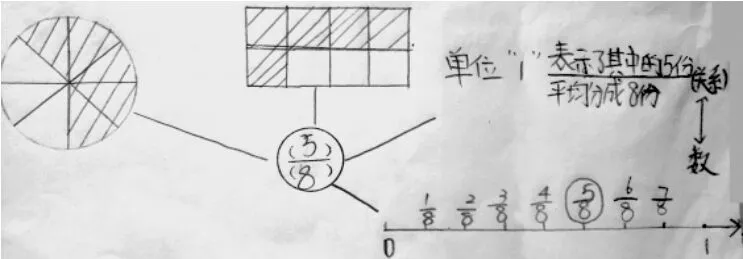
图9
师:对于他的作品,有什么问题或补充吗?
生:谢谢你的建议,以后我会注意的。
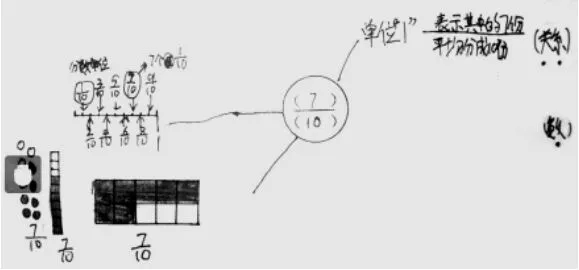
图10
生:我想给你提个建议。我发现你的数轴只画了0~1这一段,如果后面加个箭头,这样会更好。因为数轴是可以无限延伸的。
生:我建议你把数轴画到右边来,这样,我们就能够更清楚地看出,分数既能够表示关系,又能够表示一个具体的数。
生:谢谢你们的建议,以后我会注意的。
五、从零散到整合,升华认识
师:刚才,每一个同学都选择了一个分数,从不同角度表达了自己对它的理解。现在,请大家结合相应的作品,比较这些不同的分数,你觉得它们有没有什么相同的地方?
生:我觉得无论什么分数,我们都可以画图表示出来。
生:我觉得任何一个分数,都是把单位“1”平均分成几份,取其中的几份。
师:是的,数学上,把单位“1”平均分成若干份,表示这样的1份或几份的数,就叫作分数。
生:我觉得,所有分数,都可以在数轴上找到它们的位置。
师:不过,刚才我们只是在数轴上找到某一个分数的位置。试想一下,如果我们把这几个不同的分数在同一条数轴上表示出来,你有什么感觉?
生:我觉得有点乱。
生:我觉得有点麻烦。
师:事实究竟怎样,让我们一起来看一看。
(教师借助课件演示在同一数轴上找到4个不同分母的分数的过程,如图11)

图11
生:我觉得好乱啊!
生:我都看不清楚了!
师:试想一下,如果我们表示的不是4个分数,而是 4 个不同的小数,比如 0.2、0.3、0.7、0.9,情况还会这样吗?
生:不会!
生:如果是小数,看起来就清楚多了。
(教师借助课件演示同一数轴上4个不同的小数,如图12)

图12
师:同样在数轴上表示4个数,为什么分数看起来如此凌乱不堪,而小数却显得井然有序?
生:我觉得分数的分母不同,所以平均分的份数也不同,表示起来非常乱。但小数都是把单位“1”平均分成10份,所以,看起来就比较清楚!
生:我反对!这几个小数都是一位小数,如果是两位小数、三位小数呢?
生:我觉得也一样!两位小数,我们只要把单位“1”统一平均分成100份就可以了;三位小数,我们只要把单位“1”统一平均分成1000份就可以了。不像分数,几乎每一个不同的分母,我们都得重新分一次。所以,还是分数看起来要更乱一些。
师:有比较才有鉴别。和小数比较,相信大家对分数的特点感受更明显了。现在,请大家回想一个问题:如果让你到生活中去找一个数,你觉得找分数和小数,哪一个更容易?
生:我觉得找小数更容易。
生:我也觉得找小数更容易,超市、菜场、商场,哪儿都能找到小数。
师:现在,你知道这一现象背后的原因了吗?我们生活的世界,遵循着优胜劣汰的原则,其实,我们的数学世界,何尝不是如此呢!正因为分数的分母各不相同,导致分数的单位各不相同,从而给我们的比较、计算、解决问题等带来很大的麻烦,所以,日常生活中,分数离我们越来越远。好在,人们逐渐认识到分数的这一缺点,又对分数进行了一些改造,并发明了一种全新的数。这一内容,我们将在后面的学习中继续来研究!

