强化图形引领 彰显数学魅力

张建

[摘 要] 在数学的教学过程中，我们所要渗透给学生的不仅仅是知识与技能，还需要在知识与技能的建构过程中帮助学生积淀相应的思想与方法. 其实，高中数学阶段有很多的思想与方法需要教师用心去渗透和灌输，需要学生用心去积淀和领悟.

[关键词] 数形结合；概念；问题；总结

“数形结合”在数学的学习过程中是最为常见，也是最为重要的一种思想方法，这既是在问题解答之中适用范围十分广泛的一种思想方法，也为我们揭示出了高中数学知识学习的一条捷径——图形. 但是，在部分学生的心目中，总会用惯常的思维来认识“数形结合”——那就是只有在具体数学问题的解答过程当中才会借助到图形. 实际上，这种想法是十分狭隘的. 从某种程度上来讲，数学教学就是一门图形的艺术，图形的加入，往往会使得抽象的理论内容具体化、灵活化，为知识的理解提供了极大便利. 因此，图形不仅仅是问题解答的导航员，更是课堂学习的引领者. 笔者结合实际的案例，谈谈如何强化图形在数学教学过程中的引领价值，如何深化它对学生数学思想积淀的影响.

[?] 图形引领概念建构，深入细节坚实基础

从知识接受顺序来讲，概念是数学学习的开端，也是知识建立的基础，高中数学的概念构建越来越复杂、抽象. 而数学概念的理解又是数学学习的关键所在，更是学生开展后续数学学习和应用的基础. 而且概念的建构过程也突显了高中数学的精炼、抽象、复杂等特点. 虽然从文字表面看来，高中数学概念的篇幅并不长，却往往蕴含着丰富的内涵. 往往简单几十个字，就足以通过很多道习题来予以检验. 而概念的建构过程又是那么曲折复杂，在建构的过程中更需要讲究方法与技巧，更要在长期的学习过程中积淀相应的方法与技巧，最终转化为学生的数学思想，提升學生的数学自主学习能力. 因此，仅靠学生一方的努力，是很难达成我们预设的效果的，很难提升学生的自主学习能力，也很难将数形结合的方法巧妙地渗透到概念的架构之中. 而这就需要我们教师在概念架构的教学过程中把概念与数形结合进行衔接，将概念的全部含义把握准确，将数与形巧妙地合为一体，让学生在图形的引领下，轻松自如地达成对概念的深入理解.

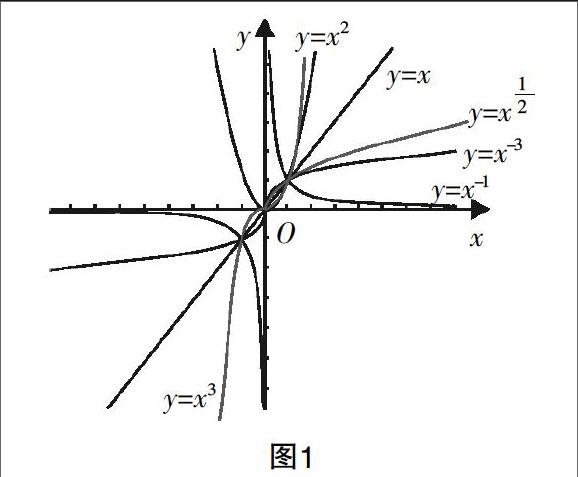
【案例1】 在幂函数的概念建构过程中，仅从字面上来看十分简单，定义如下：一般地，函数y=xa叫作幂函数，x是自变量，a是常数. 然而，其中却包含了a的不同取值所代表的不同形态的函数. 为了让幂函数的概念全面细致地展现出来，笔者在对这个内容进行教学时，结合学生已经建构的其他函数的概念和图像，引领学生将不同形态的幂函数图像集中在了同一个平面直角坐标系当中（如图1）. 由此，学生得以一目了然地看到了幂函数的全部，并对结合不同形式的幂函数的表达和图像的差异建构了一个较为完整的认知，学会了判断和辨别. 如果没有图形的辅助，这一细节是很难从文字上体现出来的. 除此之外，在概念的建构过程中，教师可以借助图形的逐一呈现来协助概念的逐一达成，能让概念的抽象慢慢显现，让学生在图形的引领下完成对概念的逐一建构，变抽象为形象，变复杂为直观.

教师如果站在学生的角度去审视数学概念的话，许多知识难免晦涩难懂. 而如果加入了图形，便可以开辟一个新的途径来诠释概念. 图形的方式，不仅让冷冰冰的数学概念重新焕发出了生命力，还可以在图形表示的同时，为学生展现出概念当中的许多细节，让学生结合图像对概念理解得更深、更细、更广. 这些细节，都是学生在常规学习过程当中十分容易忽略、混淆的，却是对学习效果具有决定性作用的. 在图形的引领之下，关键细节得到凸显，关键的难点和重点也得了突破. 此时，坚实的知识基础也就此打下了.

[?] 图形引领问题分析，一目了然清晰思维

在高中数学当中，冗长复杂的问题比比皆是. 面对这些问题时，如果只是对着文字本身展开思考，目光必然是狭隘的，思维也自然无法开阔. 这时，便需要图形的引领与帮助. 在知识内容教学的同时，笔者在教学过程中，还十分重视对学生图形构建能力的培养，甚至要求学生将画图变成自己面对数学问题时的一个条件反射，能习惯性地利用数形间的彼此转化来达成对知识的架构、难点的突破、方法的锁定. 这种情况下，图形对于问题解答的帮助就更为明显了，学生一旦能在平时的解题中顺其自然地养成这样的习惯，那么很多问题便会在无形当中显现出来，迎刃而解.

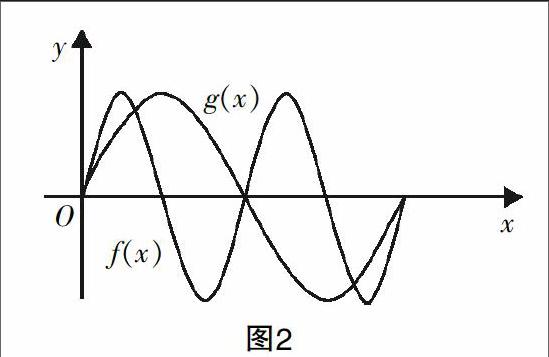
【案例2】 三角函数一直是图形引领的典型领域，也是高中数学的重点、难点之一. 当学生结束了对三角函数基本知识的学习之后，笔者提问：“请运用三角函数的相关知识判断方程sin2x=sinx在区间（0，2π）中解的个数是多少.”问题虽然简短，却让很多学生找不到头绪. “这个方程应该怎么解？”“好像没学过啊……”看到大家犯难的样子，笔者及时启发：“不然先试试把这两个函数的图像画出来吧！”这个并不难. 当学生在同一直角坐标系中开始画第二个函数的图像时，便恍然大悟：两个图像的交点不就是这个方程的解吗？（如图2）何苦再去解方程呢？只要从图像上数出交点的个数就够了. 多么巧妙的图形思维！

在复杂问题的分析解答过程当中，图形就像是另一种语言，以一种具体、生动的方式对解题过程进行展现和突破；图像更像一把万能钥匙，它随着具体情况的变化而变化，打开所有突破的智慧之门. 也正是在图形的辅助之下，学生更加清晰地明确了题目中已知条件之所述，与此同时，也得到了思维上的启发，找到了解答问题的突破口. 图形用其直观形象的线条反馈它所能表达的特点和信息，引领学生的思维，让问题显现、思路清晰、方向明确. 这些思维收获，都是单纯的文字所无法在问题突破环节，图形的协助不仅巧妙地突破了原先问题中的难点，还有效地帮助学生感受到数学学之有法、用之有道，感受到方法的重要性、图形的重要性，在学习方法上启迪了学生的智慧，激励了学生的信心.

[?] 图形引领知识总结，有机整合简洁高效

高中阶段的数学知识与技能的量是非常巨大的，而且难度也在日益增加，学生面临的不仅仅是知识与技能的理解，更是思想与方法的应用. 想要将这些内容全部清晰地掌握住，就要做到阶段性、系统性、方法性的总结与归纳、分析与对比. 而在这个总结与归纳的过程中，巧妙地运用图形，总是可以实现零碎知识点的有机整合，让学习过程简洁高效. 教师如果巧妙地借助图形进行系统的整理、框架的架构、思维的再现、方法的点拨，那么总结的效果将更加显著，且可以辐射得更广、更深、更科学.

【案例3】 笔者在带领学生学习过柱体、椎体和台体的体积计算问题之后，抓住三者之间的内在形态联系，在课堂活动中，通过教师的提问、学生的回答，在一问一答的课堂互动中，激发学生的思维，启发学生的智慧，为学生呈现出了下面的图形（图3）.

图中不仅涵盖了上述几种几何体，还形象地体现出了相互之间的动态变化过程. 在此基础上，再将每种几何体的体积计算方法配合起来，这部分的知识内容便被巧妙地整合到一张图中了. 与零散的图形、公式相比，这种结合图形进行有机整合的总结方式，显然高效多了. 这样将这几幅图的特点、共性、差异、关系巧妙地联成一整体，学生理解的高度和深度都将得到一定程度的提升. 这样的总结为学生日后进行复习和应用指引了方向，夯实了基础，有效地帮助学生轻松愉悦地完成了学习任务，提升了学习效率.

笔者始终认为，知识总结的精髓并不在于对已有知识内容的堆积罗列，而是能够找到一个巧妙合理的方式，将所学内容的特点、规律提炼出来，从而加以整合，将知识越学越“少”，方法越提越“精”，在提炼的过程中渗透方法与思想，培养思维习惯，提升思维定位. 比如，在这里的图形对比、总结，图形便扮演了一个串连者的角色，帮助学生发现知识内容的本质，并在图形的辅助下进行合并与记忆，引导学生要善于利用数形结合、类比等方法进行总结和归纳，为学生今后的学习和应用打下扎实的基础.

通过前文当中的论述，我们可以明确地感受到，图形对于高中数学的意义远远不止是优化问题解答过程这么简单. 在任何一个教学内容与教学阶段当中，图形都发挥着不可小觑的作用. 笔者坚信，在图形的有效引领之下，高中数学教学行为可以焕发出更具活力的生机和冲劲，教学效果也将比从前理想许多.