基于传递矩阵法的磁轴承转子振动特性分析*

张宇峰， 张广明， 邓 歆

(南京工业大学,江苏 南京 211816)

基于传递矩阵法的磁轴承转子振动特性分析*

张宇峰， 张广明， 邓 歆

(南京工业大学,江苏 南京 211816)

转子是磁悬浮轴承系统的核心部件。通过Prohl传递矩阵法，建立圆盘与轴段组合的转子系统模型，计算出转动惯量、截面矩等物理量，对盘轴单元矩阵进行了推导。在转子模型的基础上进行了质量离散。使用MATLAB编程得到了自由振动下转子系统固有频率和振型图，分析了支撑刚度对固有频率的影响。

磁轴承转子； 传递矩阵法； 振型图； 固有频率

0 引 言

随着高科技的不断发展，磁轴承转子以无损耗、无摩擦、能效高等优点逐步在航空、能源、交通等行业得到了认可[1]。但是,由于转子质量偏心、磁场力分布不均匀等因素的存在，磁轴承转子的稳定性及安全系数会在高速运转的过程中受到很大的影响[2]。因此关于保证转子的工作转速低于临界转速的振动特性分析研究刻不容缓。

实际状态下转子为质量连续分布且带有弹性的系统，自由度有无穷多个。研究人员曾用特征值求解的方法来计算出转子的固有特性，但在实际状态中，转子系统的边界条件各式各样，且结构难以量化，因此工作量过于庞大，且不保证一定的精度。

随着电子信息技术的不断进步，通过计算机编程的方法来分析转子固有特性的办法逐步得到了认可。传递矩阵法正是解决转子系统固有特性问题的高效快捷的方法之一[3]。凭借其占据内存少，维数不随系统自由度的提升而提高等优势，传递矩阵法在旋转机械技术领域得到了广泛的应用[4]。本文利用传递矩阵法对转子系统进行了固有特性的分析。

1 转子系统质量的离散

在应用传递矩阵法进行分析计算之前，必须对其转子本身进行离散化处理。转子系统的离散主要分为系统质量的离散和转动惯量的集中等效。

质量离散化通常即为把质量连续分布的弹性系统离散为集中质量的多自由度系统。如图1所示为呈阶梯状况下带有弹性系统的轴段，目的为简化成如图2所示的由轴段和圆盘组成的多自由度盘轴系统。即沿着轴线将转子的质量和转动惯量集中到若干结点上；结点位置的选择通常在转子系统规格突变的截面处或是典型的转子部件的中间位置，如磁轴承转子、飞轮的质心处。转子的长度、刚度则集中在相邻结点的长度上。

传递矩阵法将转子系统分为有质量、转动惯量但没有厚度、形变的刚性薄圆盘；有长度、WS刚度但没有质量的弹性轴段。

一般相邻结点间的轴段由若干不同截面大小的子轴段组成。这里不妨设其中之一的轴段序号为j，里面有s个子轴段。假设j轴段的长度为lj，其中的子轴段k(k=1,2,3,…,s)的质量、长度、极转动惯量、直径转动惯量分别为μk、lk、Jpk、Jdk。k轴段的质心离j轴段左段的长度为ak。此阶梯轴可简化为图3右图所示两端为刚性薄圆盘，中间仅一段的弹性轴段的两盘一轴模型。这里j轴段的两端结点集中了质量与转动惯量，而j轴本身化作截面尺寸相同的弹性轴。

图1 阶梯轴示意图

图2 多自由度盘轴系统示意图

图3 j轴段示意图及盘轴模型

质量集中的原则是质心的原有位置不变，即可理解为简化以后轴段间两结点刚性圆盘的总质量与简化之前的转子系统总质量相同。质心的位置与模型的状态无关，不随模型的简化而改变。根据质心位置公式可得出：

(1)

转动惯量集中等效的原则是转动惯性不变。即不随简化后模型的改变而改变，轴段间两节点刚性圆盘的转动惯量与简化之前的转子系统总转动惯量相同。图4为等截面子段转动惯量等效示意图。

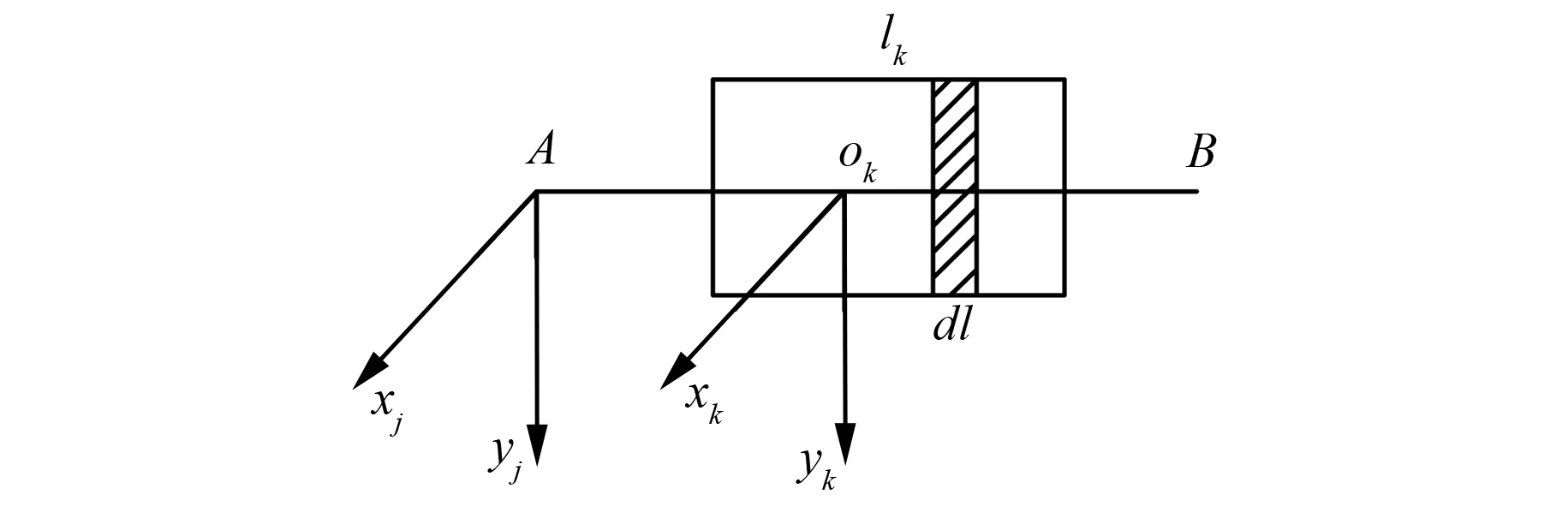
图4 k轴段转动惯量的集中等效示意图

j轴段里子轴段k的转动惯量向j轴段等效的原则为等效后的转动惯量向原惯性主轴过ok的xk与yk轴折合时保持不变，且j轴段上子轴段k上dl微元的转动惯量，等同于两端的转动惯量与到两端距离的平方成反比。

经过推算,j轴段的等效惯量为

(2)

式中:Jpk——k段截面的极转动惯量；

Jdk——k段截面的直径转动惯量。

2 转子系统模型的建立

2.1 有质量、转动惯量的刚性薄圆盘传递矩阵

对于旋转机械的第i个截面，设状态向量为Zi，由径向位移Yi、挠角αi、弯矩Mi及剪力Qi所组成，即Z=[Y,α,M,Q]T。任一轴段左右节点之间的状态向量都存在一定的关系，即Zi+1=TiZi。Ti称为截面之间的构件传递矩阵。为了便于分析计算，圆盘与轴段通常组合成一个统一构件。对转子系统进行简化，如图5所示为n个有质量、转动惯量但没有厚度、形变的刚性薄圆盘；n-1个有长度、刚度但没有质量的弹性轴段。

图5 刚性薄圆盘弹性轴模型

(3)

式(3)为圆盘i的点传递矩阵，即带弹性支撑有质量的圆盘单元传递矩阵。

2.2 无质量等截面的弹性轴段传递矩阵

对轴段i进行受力分析，如图6所示。为了综合考虑到相邻结点间的关系，其中结点i右端的剪力、弯矩表示轴段i左端的剪力、弯矩的上标。结点i+1左端的剪力、弯矩表示轴段i右侧的剪力、弯矩的上标，而不用轴段i自身的弯矩、剪力表示。

图6 轴段i受力图

当轴段i发生形变时，右端相对于左端而引起的位移由左端转角的位移、右端剪力、弯矩引起的位移共同组成。

(4)

(5)

(6)

(7)

通常ks称为截面形状系数，一般实心圆轴为10/9，薄壁空心轴为3/2；ksli/GiAi表示为剪切的形变量对弯曲的形变量的影响系数。A为截面积，EI为材料弹性模量与轴段截面矩之积。

2.3 组合件的传递矩阵

将圆盘、轴段的传递矩阵相结合可得出组合件的盘轴单元的传递矩阵，i单元至i+1单元的传递关系为

(8)

故盘轴单元的传递矩阵为

(9)

3 传递矩阵法求解磁轴承转子系统固有频率

3.1 转子模型的离散

以该转子模型为例，考虑到简化模型质量块越多，即对应的结点越多，结果会越精细。由于轴系的固有频率和振型与转子模型质量分布有关，所以简化后的模型质量，即圆盘的集质量应尽量与转子部件质量接近。

由于实际状态下的磁轴承起到弹簧的作用，磁轴承转子所受悬浮力近似为弹簧对磁轴承转子的作用力，即两径向磁轴承的悬浮支撑力近似为两个弹性支承，所以设每个弹性支承由起到刚度作用的弹簧组成，等效模型如图7所示。本文将转子离散为28个轴段，图8所示为转子模型的离散示意图。其中每个黑点即结点，是转子部件所对应的质量单元，结点的质量即为黑点前轴段质量的一半与后轴段质量的一半之和，共29个结点。本例中左径向磁轴承转子为第8个结点，右径向磁轴承转子为第20个结点，飞轮为第27个结点。

图7 磁轴承支承等效模型

图8 转子模型离散图

离散化后转子各轴段的具体参数如表1、表2所示。

表1 离散化后转子各轴段具体参数

3.2 实例求解

通常设刚性支承为理想状态下的轴承支承，故这里从刚性入手分析。设左右磁轴承等效支承刚度5×107N/μm作为绝对刚度，即相当于刚性支承。得出的转子系统固有频率和振型图如图9所示。基于刚性支承的转子系统前四阶固有频率如表3所示。

表2 离散化后转子各轴段具体参数

图9 基于刚性支承转子系统前四阶振型图

图9按照从上到下的顺序依次排列，分别为转子刚性支承状态下的前四阶振型图。图9中横坐标为转轴总轴段的长度，单位为m，纵坐标为磁轴承转子系统发生共振时的径向位移，单位为μm；圆点即所对应的结点，实心圆点即为左右磁轴承支承所对应的结点，分别位于转轴的0.160 m和0.325 m处。根据圆点位置的不同可得出共振时转子径向位移的大小。由图9可得结点处位移量始终为零，符合刚性支承处固定的要求。前三阶主要表现为最后一个结点的径向位移，第四阶表现为整个磁轴承转子剧烈的上下摆动。所以前三阶发生共振时的径向位移主要在转轴前端，即飞轮处形变量较为明显，第四阶的位移量发生骤变，说明发生了强烈的共振。

表3 基于刚性支承的转子系统前四阶固有频率

但是实际状态下的磁轴承支承为完全弹性支承。对磁轴承支承的等效刚度参数用弹簧来模拟。通过改变支承刚度的值可以得到所对应固有频率的值。如表1所示，在第8和第20结点处作为磁轴承转子的位置。输入不同等效支承刚度k的大小即可得到相对应的固有频率。前后输入支撑刚度为50 N/μm，步长为200的刚度值递增。将以上数据连同组合件得出的传递矩阵，导入MATLAB传递矩阵法编译的程序中。

图10 50 N/μm转子系统前四阶振型图

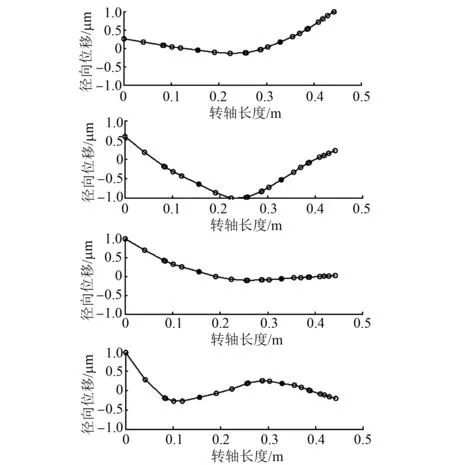
图11 250 N/μm转子系统前四阶振型图

由图10～图15可知，前两阶主要表现为平面内的径向摆动，磁轴承处对应的结点位移量微小。第一阶共振时的最大径向位移位于末端结点，即飞轮处；第二阶最大径向位移位于起始结点，即转轴末端。由前两阶振型图相似的特点可知低阶状态下转子系统的固有频率变化微小，而后两阶振型图差异较大，可知高阶状态下转子系统的固有频率变化较大。由图11、图12的第三阶振型图可知，轴段的0.2～0.25 m处为共振时的最大径向位移，即转子系统的电机转子处径向位移最大。由图13、图14的第四阶振型图可得知，轴段的0.05～0.1 m处所对应的径向位移较大。由图15的第四阶振型图可知，轴0.15～0.2 m处所对应的径向位移较大。

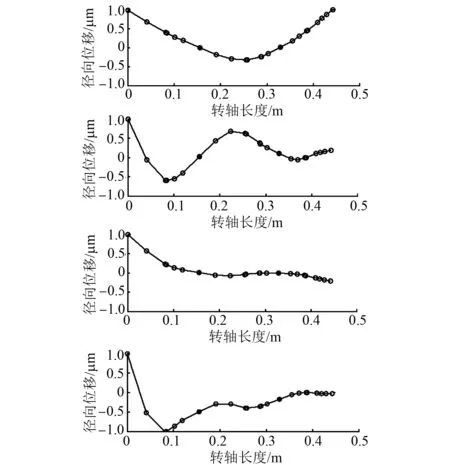
图12 450 N/μm转子系统前四阶振型图

图13 650 N/μm转子系统前四阶振型图

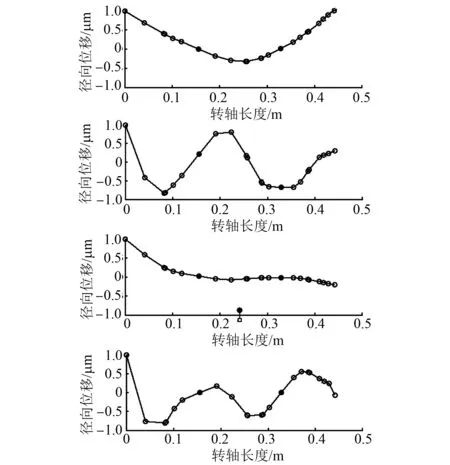
图14 850 N/μm转子系统前四阶振型图

图15 1 050 N/μm转子系统前四阶振型图

根据转子系统的最高转速6×105r/min可得出转子系统的最高运转频率为1 000 Hz。由表4可知，当支承刚度为50 N/μm、250 N/μm时，前三阶转子系统固有频率均小于磁轴承转子系统的最高运转频率1 000 Hz，故理论上该转子系统在运转频率下很难稳定工作；而随着刚度的提升，固有频率逐步增大。当支承刚度大于250 N/μm时，三阶、四阶固有频率均大于1 000 Hz，超出转子最高运转频率，所以不作考虑。说明可以通过提升弹簧支承刚度的方式，让转子系统本身运作时的频率远离固有频率，从而降低共振的风险。由表4与表3所得数据进行对比，结果发现当轴承为刚性支承时，固有频率最高；弹性状态下当弹簧支承刚度值逐渐增大时，固有频率也逐渐趋近于一个最大值。

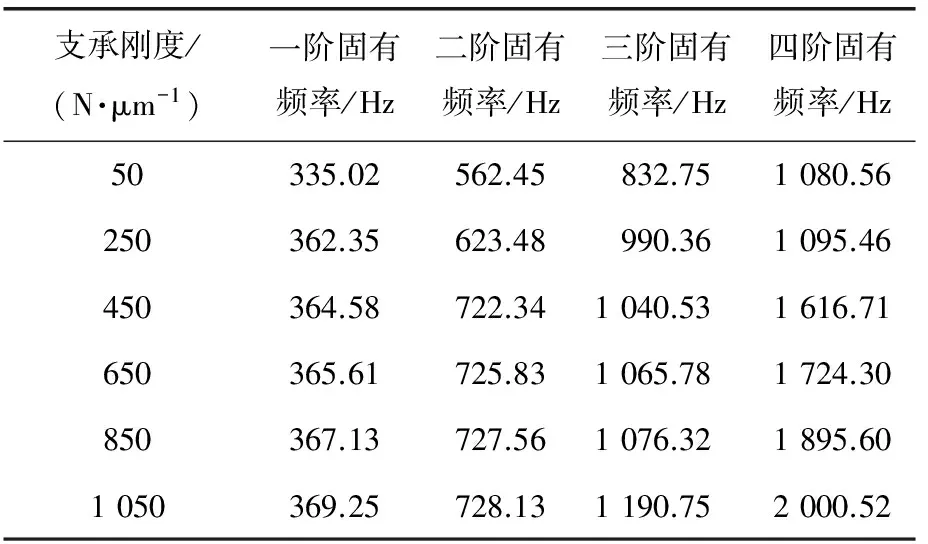
表4 不同支承刚度下的转子系统前四阶固有频率

4 结 语

本文利用Prohl传递矩阵法，建立了圆盘与轴段组合的转子系统模型，计算出了转动惯量、截面矩等物理量，对盘轴单元矩阵进行了推导和论述。在建立转子模型的基础上，本着质心不变的原则进行了质量离散。使用MATLAB编程得到了自由振动下转子系统固有频率和振型图。分析发现磁轴承的等效弹簧支承刚度对转子系统固有频率有很大的影响。当弹簧刚度为理想状态下的刚性时，固有频率最高；当为实际状态下的弹性支承时，转子系统的固有频率会随着弹簧支承刚度的提高而提高。因此可以通过增加支撑刚度的方式提高系统固有频率，让转子系统的运转频率远离固有频率，从而降低共振的风险。

[1] 吴华春.磁力轴承支承的转子动态特性研究[D].武汉： 武汉理工大学，2005.

[2] 刘建武，顾力强.动力传动轴临界转速设计研究[D].上海： 上海交通大学，2007.

[3] 袁惠群.转子动力学基础[M].北京： 冶金工业出版社,2014.

[4] 孟杰，陈小安.电主轴动力学分析的传递矩阵法[J].机械设计，2008，25(7)： 37-40.

中文核心期刊 中国科技核心期刊 中国学术期刊(光盘版)

全国优秀科技期刊 华东优秀科技期刊

中国科学引文数据库来源期刊 中国学术期刊综合评价数据库来源期刊

Analysis of Vibration Characteristics of Magnetic Bearing Rotor Based on Transfer Matrix Method*

ZHANGYufeng,ZHANGGuangming,DENGXin

(Nanjing Tech University, Nanjing 211816, China)

Through transfer matrix method built a disk and shaft segment combination of rotor system model to calculate the moment of inertia, section moment and other physical quantities, on the disc axis unit matrix were derived and discussed.The quality based on the discrete model of the rotor.Using MATLAB programming to get the free vibration of rotor system inherent frequency and vibration type graph, and analyzed the influence of support stiffness on the natural frequency.

magnetic bearing rotor; transfer matrix method; vibration map; natural frequency

国家自然科学基金项目(51277092);江苏省基础研究计划(自然科学基金)资助项目(BK20130938);江苏省高校自然科学研究项目资助(14KJB510013)

张宇峰(1992—)，男，硕士研究生，研究方向为电机控制。 张广明(1965—)，男，博士/博士后，教授，博士生导师，研究方向为机电系统综合控制。 邓 歆(1982—)，男，博士研究生，硕士生导师，研究方向为磁链观测器设计，无速度传感器控制技术。

TM 303.5

A

1673-6540(2017)03- 0071- 07

2016 -09 -20