模块化多电平变换器环流及电容电压的稳态解析表达式

陈耀军 刘 幸 赖向东 秦振杰

（空军预警学院黄陂士官学校，武汉 430345）

模块化多电平变换器环流及电容电压的稳态解析表达式

陈耀军 刘 幸 赖向东 秦振杰

（空军预警学院黄陂士官学校，武汉 430345）

环流谐波及电容电压波动是模块化多电平变换器（MMC）的一个重要研究课题。本文通过一个MMC的等效模型推导出了由输出电流引起的环流谐波及电容电压波动的解析表达式，指出环流谐波本质上是存在于系统直流侧的谐波电压引起的激励，分析了环流谐波相生的原理。根据表达式，分析了系统参数对环流谐波的影响，得出结论，即环流谐波幅值随系统频率等参数的变化呈谐振特性。最后通过仿真研究证实了所提表达式的正确性。

模块化多电平变换器；环流谐波；电容电压波动；解析表达式

在2003年的一次国际会议上，Lesnicar A和Marquardt R首次提出了模块化多电平变换器（MMC）的拓扑结构和工作原理[1]。图1所示为其三相拓扑结构图，其由6个桥臂组成，每个桥臂由N个模块和一个电感组成，模块是一个半桥式结构。由于这种拓扑结构具有模块化特点，电压扩展十分方便，十分适合在中高压应用，因而其一经提出，便引起了业界人士广泛的关注[2-3]。

MMC一个重要特点是存在着相间环流，环流存在直流分量和交流分量，直流分量用于调节模块电容的能量，而交流成分则是能量变换过程中的伴随产物，其会增大系统损耗和开关管的电流应力。与此同时，模块电容电压也存在着波动。因此，研究MMC环流谐波及电容电压波动的成因及影响因素，是MMC研究的一个重要课题。

文献[4]分析了环流的特点，但没有研究其成因。文献[5]通过求解系统变量之间的非线性微分方程，系统全面深入地分析了桥臂电流的谐波内容及表达式，从其表达式可以看出，环流谐波间互为包含，要得到最终表达式还需根据具体情况进一步推导。文献[6]从功率流动的方法得出模块电容电压波动的表达式，但该表达式和电容电压相关，没有得出一般性的解。文献[7-8]通过忽略环流谐波的方法得出了电容波动表达式，不具有一般性。

图1 模块化多电平变换器拓扑结构

本文作者在文献[9-11]中提出了MMC的一个等效模型。该模型精确、直观地反应出了MMC变量之间的相互关系。根据该模型，本文推导出了环流及电容电压的解析表达式，该表达式只与输出电流、调制函数以及系统参数有关，从而具有一般性，根据得到的环流谐波表达式分析了系统参数对谐波幅值的影响，最后通过仿真证实了推导的表达式的正确性。

1 环流谐波表达式

1.1 MMC等效模型

若忽略载波的影响，并且假设上下桥臂是对称的，则文献[9]推导出了MMC的系统状态方程，以u相为例，现直接引用如下：

根据式（1），文献[9]给出了系统的u相等效模型，如图2所示。

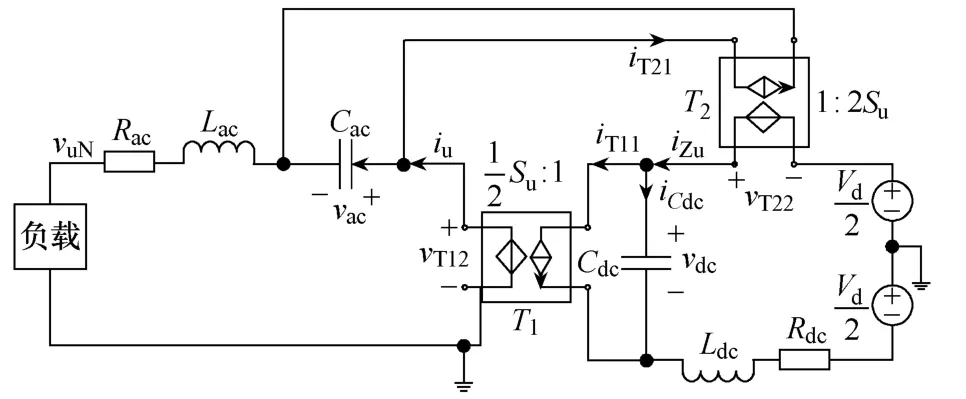
图2 系统u相等效模型

1.2 环流谐波表达式

显然，图2中直流回路的电流即为系统环流。从图2中可以看出，环流的直流成分用于给输出提供有功功率，若输入直流电源不变，则影响环流谐波的因素有两个：①负载电流通过逆变器T1的调制作用；②是电容电压vac通过网络T2的调制作用。为讨论由输出电流引起的环流谐波，不防假设环流谐波已被抑制，此时环流中只有直流成分，从T1的输入输出关系中可以发现，由于输出电流iu通过T1的调制作用，使得T1初级电流iT11由直流和二次谐波组成，显然其中的直流成分和环流直流相同，而谐波成分会在电容Cdc中产生二次谐波电压。与此同时，直流环流通过T2会向Cac注入一个基波电流，该电流和负载电流iu一起，在Cac中产生基波电压，该基波电压通过T2的作用，会在直流回路中产生一直流和一二次谐波电压。由此可见，此时（环流谐波被抑制）直流回路中会存在由输出电流引起的两个二次谐波电压，若把这两个谐波电压合并，则可由式（2）确定[10]。显然，如果去掉环流抑制的措施，这个二次谐波电压就会通过电路间的相互作用产生谐波环流。这一环流产生的过程可以通过图3进行说明。图中：

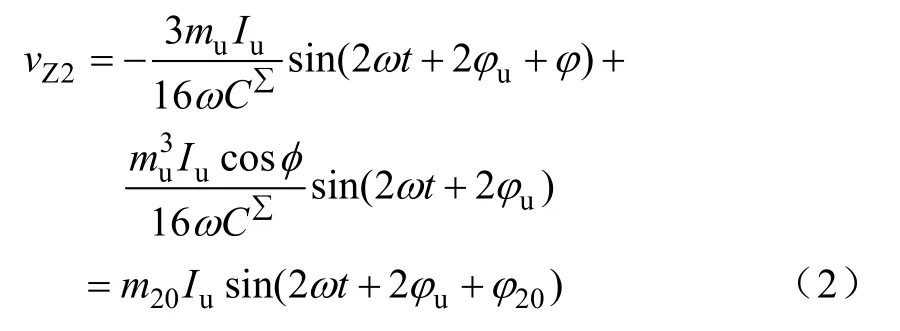
式中，

Z(n,n+2)、Z(n,n)和Z(n,n-2)分别被定义为n次谐波环流通过电容Cac的反馈作用在直流侧生成的n+2次、n次和n-2次谐波电压的阻抗，其表达了环流和电容Cac电压vac之间的相互影响，其表达式如式（3）至式（5）所示[9-10]，Y(n)为直流回路n次谐波导纳，如式（6）所示。环流的n次谐波，会在电容Cac上产生n-1和n+1次谐波电压，该谐波电压又会反作用到直流侧，产生新n+2和n-2次谐波环流。这样，一个n次谐波电压，会在环流中产生n±2k（k=0,1,2,…）次谐波，在电容Cac中产生n±2k+1次谐波，这就是环流谐波相生的原理。

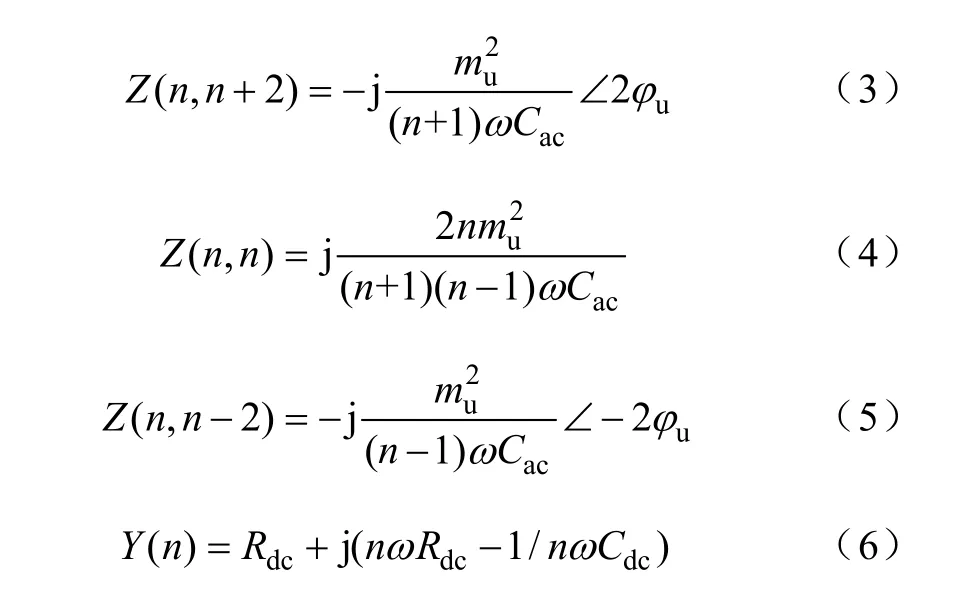
显然，在二次谐波电压的激励下，利用谐波相生原理，会在环流中产生无穷偶次谐波，在电容Cac中产生无穷奇次谐波电压。虽然理论上环流会含有无穷偶数次谐波，电容Cac含有无穷奇数次谐波电压，但实际上各次谐波电流或电压的幅值是递减的，一般环流可以忽略六次及以上谐波，电容Cac可以忽略五次及以上次谐波。

从图3可以看出，环流谐波的产生过程事实上是直流侧的谐波电压在给系统的激励过程中产生的，其产生过程遵循谐波相生原理，因此图3所体现的谐波产生原理适用于任何施加于直流回路的谐波电压。在正常工作情况下，直流回路中会产生二次谐波电压vZ2，该电压来源有两个：①输出电流通过T1产生于；②Cac上的基波电压通过T2产生，但根本上讲是由输出电流产生的。通过vZ2的作用，便产生了上面分析的环流谐波及电容电压谐波。

如果不考虑四次以上谐波的影响，只考虑二次和四次谐波，则可以解出四次和二次谐波表达式为

式中，

从式（8）可以清楚看出，该谐波是由输出电流引起的，其只与输出电流幅值、相位、桥臂电感、模块电容及调制比有关，知道了这些参数就可以计算出环流谐波的实时值，因此这个表达式可以认为是环流谐波的最终解。

mf2表征了输出电流幅值向二次环流谐波幅值的传递特性，其是系统调制函数的函数，并且和系统参数有关。因此，mf2可以作为研究由输出电流引起的环流谐波幅值的特征函数。

从式（8）还可以看出，调制函数的初始相位在二次谐波环流中翻倍，而ϕ2是一个固定值，只与系统参数有关，这样，三相二次谐波环流将呈负序分布。

图3 环流谐波产生的因果关系图

2 环流谐波影响因素分析

从上面的分析可以看出，环流谐波是在vZ2的激励下产生，因此环流谐波的大小取决于vZ2，此外，取决于电路参数。从式（7）和式（8）可以看出，环流主要取决于负载电流、功率因数、幅度调制比、工作频率以及电路参数。为研究方便，忽略六次及以上次谐波，研究的对象是10kV的高压电机变频驱动系统，其一个桥臂有14个模块，模块电容为4700μF，额定频率为50Hz，对式（8）进行仿真研究。假设负载电流不变，且归一化，则mf2反映了二次谐波电流幅值相对于负载电流幅值的增益。根据应用平台可以得出仿真参数为：Cdc=671.4μF，mu=1，Ldc=4mH，Rdc=1Ω，ω=314rad。

图4和图5给出了两个参数同时变化时环流谐波增益变化三维曲面图。

图4（a）为环流二次谐波幅值随幅度调制比mu和负载功率因数角ϕ 的变化曲面。当mu较小时，环流二次谐波幅值较小，随负载功率因数角ϕ 的变化，其幅值波动较小，但在mu较大时，环流二次谐波幅值较大，在此区间内，曲面随ϕ 的变化波动较大。可以看出曲面是按照余弦规律变化的，在mu=0.8附近，ϕ =±π/2时，存在着两个谐振峰。

图4（b）为环流二次谐波幅值随系统角频率ω和电感Ldc变化的波形，其电感Ldc的变化范围为0～50mH，角频率ω 的变化范围为0～500r/min，Ldc和ω变化范围内分别均匀采样25点。图中的曲面就像一座山坡，中间高，两边低，右边高，左边低，坡的最高点连成一条线，就叫“山脊”线，其是一条起伏的曲线，线上的每一个点，表示固定频率或电感而变化另一变量，环流二次谐波能取得的最大值，离开该点，环流二次谐波幅值逐渐减小。“山脊”线是一条曲线，贯穿左右对角线，频率越大，曲线越缓，并且高度很小，对应的电感值也较小，随着频率值的减小，“山脊”线逐渐向上翘，并且上翘的速度越来越快，这意味着角频率的减小，环流谐波取得最大值以及所需的电感值都随之增加。虽然图4（b）是在特定的电容下得出的，不同的电容值会得到不同的曲线，但其变化趋势是基本相同的。

图4（c）和（d）为环流二次谐波幅值分别随角频率ω 和等效电阻Rdc及电感Ldc和电阻Rdc变化的曲线。Rdc为直流回路的等效电阻，其包括线路电阻，IGBT模块开关损耗、开通损耗以及死区效应等的等效电阻。由于系统是若干个模块的串联，因此Rdc相对不会很小。另一方面，由于IGBT的开通压降变化不大，因此其开通等效电阻具有非线性特性，流过的电流越大，其等效电阻越小，反之流过的电流越小，其等效电阻越大。因此，系统的等效电阻和负载电流有关系，负载电流越大，Rdc越小，负载电流越小，Rdc越大。图中Rdc的变化范围为0.1～5Ω，ω 的变化范围为0～500r/min，Ldc的变化范围为0～10mH。在两图中，均可以发现，Rdc靠近0时，无论是随ω 变化还是随Ldc的变化，均存在谐振峰，并且，Rdc越小，环流谐波峰值越大，但随着Rdc的增大，环流谐波峰值快速衰减。这意味着如果串联的模块越多，而工作电流很小，环流谐波的相对峰值就越小。

图4 环流二次谐波幅值随参数变化的三维仿真图

图5所示为环流四次谐波幅值随系统角频率和电感的变化曲面，可以看出，曲面形状和二次环流谐波幅值对应的曲面形状相似，但幅值增益大大减小，如果要精确估计环流二次谐波幅值，环流四次谐波的幅值就不可忽略。

图5 环流四次谐波幅值随ω 和Ldc变化的三维仿真图

前面的讨论体现了在MMC用于高压电机驱动时，MMC的环流谐波随参数变化的特性，特别是随频率变化呈谐振特性，这对电机的变频控制很重要。需要说明的是，上面分析的谐振峰及曲线是在特定参数情况下得出的，这证明了环流谐波存在谐振特性，但这一特性并不依赖于特定的参数，只要相关参数确定，环流谐波幅值就可以被精确地计算出来。因此本文的分析方法可以推广到一般的情况。

3 电容电压表达式

根据图2可知，可以将电容Cdc的直流电压Vdc0写成

式中，IZu0为环流的直流分量，VT210为电容Cac的电压通过网络T2在直流侧产生的直流分量，其来源有两个：①环流直流和输出电流在Cac中产生的基波在直流侧产生的直流分量；②二次谐波环流通过Z(2,0)产生的直流分量，则式（9）可以写成式（10）的形式。

可见，Vdc0并不绝对等于输入直流电压Vd，通常Vd比较大，式（10）中的其他几项相对于Vd比较小，在分析问题时可以忽略。

由于负载电流的调制作用，iuc中含有二次谐波成分，该二次谐波会在Cdc上产生相同频率的交流电压，而实际上环流中含有偶次谐波，这些谐波电流必然会在电容Cdc上产生新的电压波动，简单起见，这里只考虑二次谐波的影响，如式（11）所示。

从式（11）可以看出，vdc中含有二次谐波分量，其来源有两个：①负载电流的调制作用；②环流中的二次谐波分量。环流中的二次谐波分量会加大电容的波动幅度，如果在直流回路中施加控制，使环流中不含谐波成分，电压中的二次谐波分量仍然存在，其幅值受负载电流和幅度调制比的控制。

在电容Cac中，流过负载电流和被网络T2调制过的环流，则有式（12）的形式。经整理可得式（13）。

可见，vac中主要含有基波和三次谐波分量（这里只考虑了环流中的二次谐波成分），式中的后两项由二次谐波产生，如果环流不含有谐波成分，此时电容电压的差中就仍然含有基波成分，负载电流越大，波动的幅值越大。对于上下桥臂电容总电压的波动显然可以描述式（14）和式（15）所示的形式。可见，当只考虑环流二次谐波时，上下桥臂电容电压主要含有1、2、3次谐波，上下桥臂电压中二次谐波同相，基波和三次谐波反向，幅值相同。

式中，

4 仿真验证

为了验证环流及电容电压等变量表达式的正确性，本文进行了对比仿真研究，按照实际电路用Simulink搭建了一个仿真平台，将仿真结果和公式模拟结果进行了对比分析。平台的仿真参数见表1。图6所示为仿真结果，图中左边为仿真波形，右边为根据公式拟合波形。

表1 仿真参数

图6（a）为环流及输出电流波形，对比左右波形可以看出，输出电流的仿真波形和拟合波形基波成分是相同的，仿真平台环流中的直流成分和公式计算的基本一致，环流中的交流波形，仔细对比可以发现仿真和拟合的波形有些不一致，这是因为拟合波形中的交流只叠加了二次谐波，而实际的波形中则除了二次谐波外，还含有少量的其它偶次谐波（主要是四次谐波），在当前电路参数下成分很少，可以忽略，这证实了环流中必然含有偶次谐波成分的正确性，同时也表明环流谐波中占主导地位的是二次谐波，其次是四次谐波。

图6（b）为u相上下桥臂的电流，其右边拟合波形是根据环流及输出电流叠加而成，可以看出它们基本一致，存在的误差主要由偶次谐波带来。值得注意的是，如果环流的交流成分及输出电流的幅值没变而相位发生变化（如电路参数发生变化），那么叠加后的桥臂电流波形将会发生变化。

图6（c）、（d）和（e）分别为反映上下桥臂电容电压之和的vdc、反映上下桥臂电容电压之差的vac、上桥臂电容电压之和以及下桥臂电容电压之和的波形。vdc波形中主要含二次谐波等偶次谐波，vac的波形中主要含1、3、5等奇次谐波，这与文中分析的是一致的。上桥臂电容电压之和及下桥臂电容电压之和波形中则含有各次谐波成分，两个波形的偶次谐波同相，奇次谐波反相，但幅值大小相同。

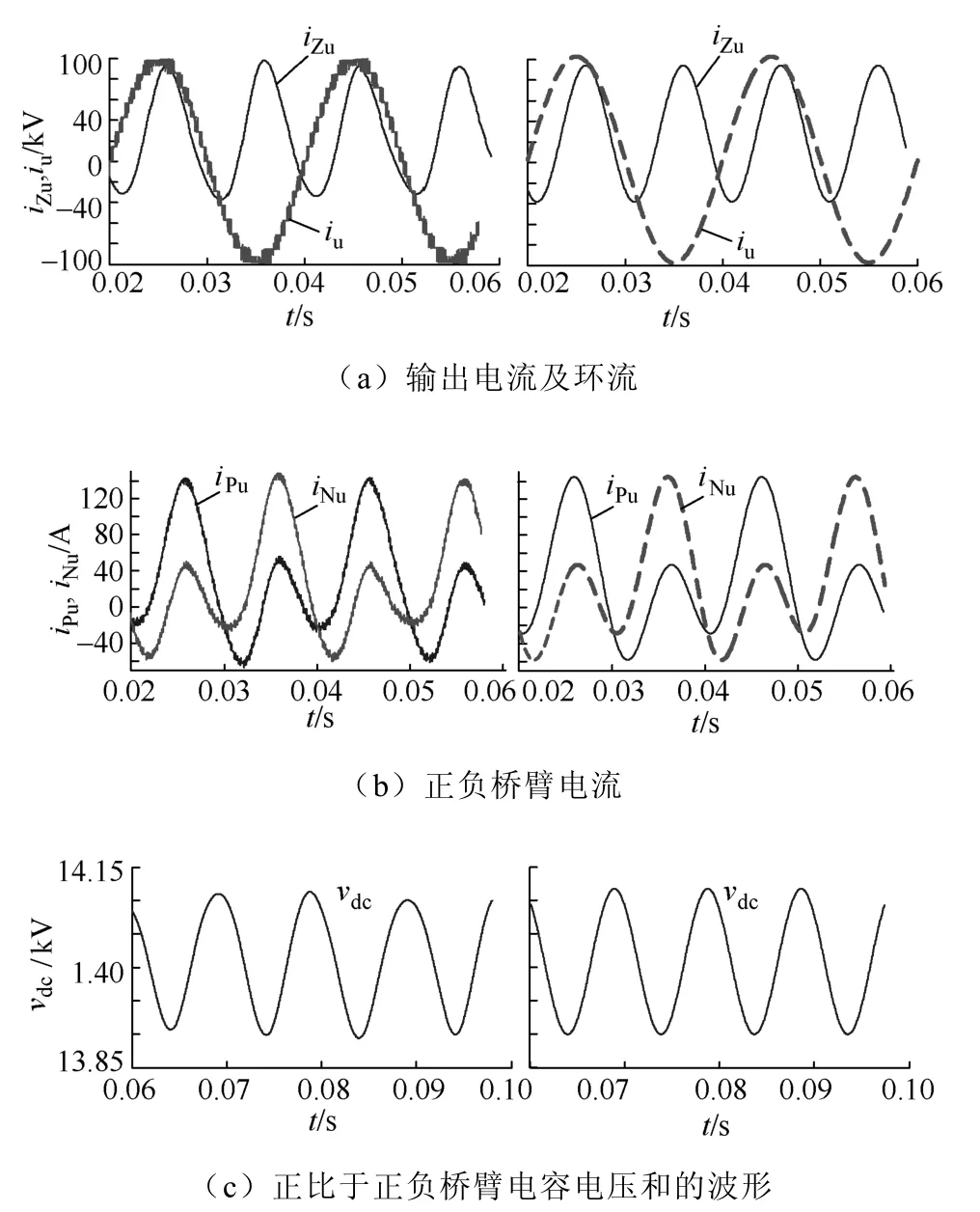
图6 仿真及公式拟合波形

为了验证参数变化对环流幅值的影响，本文利用上述仿真平台，研究改变输出频率和桥臂电感时，环流谐波幅值的变化，图7为对应的仿真结果。

图7（a）为桥臂电感不变（2mH），输出频率从10Hz变化到100Hz时，环流谐波幅值相对于输出电流幅值的增益曲线；图7（b）为输出频率固定在50Hz，而桥臂电感从0.5mH变化到10mH时，环流谐波幅值相对于输出电流幅值的增益曲线。不难发现，无论是改变输出频率还是改变桥臂电感，二次环流谐波幅值均存在明显的谐振特性，四次环流谐波也存在谐振特性，但四次谐波幅值总体相对较小，而六次及以上次谐波基本可以忽略，这与前面的分析是吻合的。因此，在设计系统参数时，特别是在电机变频驱动领域，应高度关注二次谐波的这一谐振特性。

图7 环流谐波幅值增益随系统频率和桥臂电感变化曲线

5 结论

本文在已有的等效模型基础上，分析了环流形成机理，提出了环流谐波相生的原理，在此基础上，推导出了环流及电容电压的解析表达式，该表达式是输出电流的变量，因而具有通用性。利用推导出的表达式，分析了系统参数对环流谐波幅值的影响，表明环流谐波幅值随系统频率等参数的变化而呈谐振特性。本文结论可以用于研究MMC环流和电容电压波动特性及系统参数选取。

[1] Lesnicar A, Marquardt R. An innovative modular multilevel converter topology suitable for a wide power range[C]//IEEE 2003 Power Tech Conference, 2003: 23-26.

[2] Peng F Z, Wei Q, Dong C. Recent advances in multilevel converter/inverter topologies and applications[C]//2010 International Power Electronics Conference (IPEC). Sapporo, Japan: IEEE, 2010: 492-501.

[3] Malinowski M, Gopakumar K, Rodriguez J, et al. A survey on cascaded multilevel inverters[J]. IEEE Transactions on Industrial Electronics, 2010, 57(7): 2197-2206.

[4] Ilves K, Antonopoulos A, Norrga A, H.-P. Nee: Steady-State Analysis of Interaction Between Harmonic Components of Arm and Line Quantities of Modular Multilevel Converters, IEEE Transactions on Power Electronics, 2012, 27(1): 57-68.

[5] 丁冠军, 丁明, 汤广福, 等. 新型多电平VSC子模块电容参数与均压策略[J]. 中国电机工程学报, 2009, 30(1): 1-6.

[6] 杨晓峰, 王晓鹏, 范文宝, 等. 模块组合多电平变换器的环流模型[J]. 电工技术学报, 2011, 26(5): 21-27.

[7] 王姗姗, 周孝信, 汤广福, 等. 模块化多电平HVDC输电系统子模块电容值的选取和计算[J]. 电网技术, 2011, 35(1): 26-32.

[8] 郭高朋, 胡学浩, 温家良, 等. Analysis and suppression of circulating harmonic currents in a modular multilevel converter considering the impact of dead time[J]. IEEE Transactions on Power Electronics, 2015, 30(7): 3542-3553.

[9] 陈耀军, 陈柏超, 袁佳歆, 等. 模块化多电平逆变器电容电压及环流控制[J]. 电工技术学报, 2014, 29(10): 166-174.

[10] 陈耀军, 陈柏超, 田翠华, 等. 模块化多电平变换器的系统状态方程及等效模型[J]. 中国电机工程学报, 2015, 35(1): 167-176.

Steady State Analytic Expressions of Circulating Currents and Capacitor Voltages of the Modular Multilevel Converter

Chen Yaojun Liu Xing Lai Xiangdong Qin Zhenjie
(Huangpi NCO School of AFEWA, Wuhan 430345)

The study of the circulating harmonic currents and the capacitor voltage fluctuation of the modular multilevel converter (MMC) is a hot topic, so the analytic expressions of the circulating harmonic currents and capacitor voltages in steady state based on an existing equivalent model of the MMC is deduced. During this course, it concluded that the circulating harmonic currents are essentially products of the exciting course of a harmonic voltage upon the dc loop, and the principle of the circulating harmonics produced each other. According the deduced expressions, effects of the system parameters upon the circulating harmonics are analyzed. Finally the simulation study proved the deduced expressions.

modular multilevel converter; circulating harmonic currents; capacitor voltage fluctuation; analytic expressions

陈耀军（1977-），男，湖北省鄂州市人，博士，讲师，主要从事电力电子技术研究工作。