高压电缆实时导体温度计算与载流量预测探究

赵柏山 王庆祝

（沈阳工业大学信息科学与工程学院，沈阳 110870）

高压电缆实时导体温度计算与载流量预测探究

赵柏山 王庆祝

（沈阳工业大学信息科学与工程学院，沈阳 110870）

电缆导体的实时温度是电缆是否达到载流量的判断依据。为了计算电缆的温度场，相关研究人员采用过数值分析、解析计算、试验和温度在线监测等方法。本文在构建电缆动态热路模型的基础上，结合敷设环境等条件，借助Matlab软件求得动态热路微分方程组的数值解，得到电缆温度场的实时分布情况，并预测出不同条件下电缆的可承受载流量。根据该方法也可以得到在施加阶跃电流作用下的电缆温度场的实时分布情况，并且可以计算出导体达到指定温度所需要的时间。分析结果表明，本文采用的方法不仅可以计算电缆的实时温度场和可承受载流量，还能够合理推算导体温升的时间，对相关工程实践有重要的参考意义。

高压电缆；热路模型；实时温度；载流量预测

电缆额定载流量的计算公式是国际电工委员会（IEC）根据国际大电网会议（ICGRE）1964年的报告于1982年所指定的电缆额定载流量（load=1负荷因数）计算标准。随后对该标准经过一代人修改和增补，形成了现阶段的IEC 60287标准和暂态载流量的IEC 60853标准。这也是目前大部分国家采用的电缆载流量计算标准。供电线路的电缆未必都是一直处于额定负荷工作状态，可以利用电缆未达到额定温升前一段时间，在有限的时间内，施加一个超过额定负荷的电流值，使电缆温升达到但不超过最高允许温度。这就为电缆动态增容提供了条件。

研究电缆载流量和温度场的主要方法都是基于IEC 60287和IEC 60853给出的热路模型进行计算[1-6]，后续研究人员分别采用了有限容积、有限差分和有限元等经典数值分析方法对各类复杂条件下的电缆载流量与温度场分布情况进行了研究[7-11]，也有一些研究人员和相关部门分别采用电缆表面温度在线监测的方法来研究电缆动态增容[12-16]和实验的方法来确定电缆的实际载流量[16-20]。

目前关于电缆导体温度实时计算的研究大都建立在已知电缆导体外皮温度的基础上，再根据电缆各层结构参数反推导体内部的温度。本文无需将电缆外皮温度作为已知条件，只根据环境条件与施加电流的变化直接计算就能得出电缆温度场分布，这对电缆载流量的预测与电缆动态增容都有重要意义。

本文以64/110kV YJLW02 630mm2型号电力电缆为研究对象，针对不同敷设方式编写大量Matlab程序，对电缆在固定电流负荷与阶跃电流负荷作用下，电缆各层的温度进行仿真计算，主要分析了导体和外皮温度随时间变化的响应曲线，并对每种条件下电缆温升达到最高允许温度时施加的最大电流负荷进行预测。同时将计算得到的结果与改进的IEC算法和IEC标准算法结果进行对比，验证了该方法的准确性与实用性。

1 等效热路模型

高压XLPE电缆的横截面图如图1所示，实测结构参数见表1。该类型的电缆主要由铜导体、导体屏蔽、绝缘、绝缘屏蔽、阻水层、缓冲层、皱纹铝护套、外护套等构成。

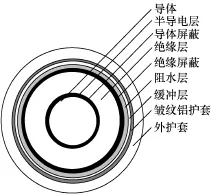
图1 110kV电缆剖面图

图2 110kV XLPE电缆暂态热路模型

文献[16]给出了电缆暂态热路的模型组成，并对该模型下电缆的暂态温度场计算进行了推导，结合64/110kV YJLW02 630mm2型号电力电缆的结构，得出单位长度该型号电缆的暂态热路模型，如图2所示。图中，Ti（i=1～7）为电缆各层实时温度，T8为外界环境温度，Ci（i=1～7）为电缆各层热容，C8为外界环境热容，在温度场计算过程中假设外界恒温，则C8趋于+∞，Ri（i=1～7）为电缆各层热阻，Qi（i=1～7）为电缆各层生热损耗，Q8为外部热源，在该文计算电缆温度场过程中不考虑有外部热源的情况，所以Q8=0，又因为电缆在运行过程中，导体本身的产热损耗、绝缘层产生的介质损耗以及皱纹铝护套产生的环流或涡流损耗远大于其他各层产生的损耗，所以Q2=Q4=Q5=Q7=0。对以上各种参数均按照IEC 60287标准方法进行计算。电缆结构参数与热属性参数取值见表1。

在应用此模型的过程中对电缆做了如下几种理想状况下的假设。

表1 电缆结构与热属性参数

1）电缆长度远大于直径，忽略轴向传热，且电缆轴对称，沿圆周方向均匀传热，只在径向存在温度梯度。

2）构成电缆各层材料的几何参数恒定，忽略温度变化对几何参数的影响，同时将各层视为等温体，在模型中作为集中参数处理。

3）导体屏蔽层、绝缘屏蔽层厚度很薄，且热阻、热容参数与绝缘层相差很小，因此将两者归算到绝缘层合并计算。

4）电缆在运行过程中，导体本身的产热损耗、绝缘层产生的介质损耗以及皱纹铝护套产生的环流或涡流损耗远大于其他各层产生的损耗。

5）计算外界环境热阻时，将环境温度当作恒温计算。

2 计算原理与方法

针对图2建立的模型，根据热路与电路的相似性，采用类似于电路中节点电压法对每一个节点列出热路平衡方程，可得方程式（1）至式（7）：

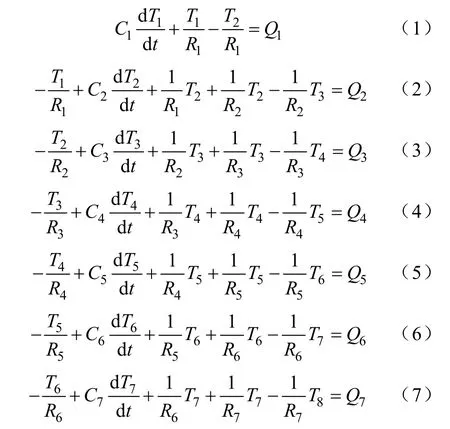
式中，对电缆本体各层热阻与热容、不同接地方式下金属护套的损耗以及绝缘层的介质损耗均采用IEC标准法进行计算。自由空气中敷设时外部环境热阻的计算式如下：式中，h为散热系数；De为电缆外径，m；对于皱纹金属套De=(Doc+2t3)×10-3；h为可利用自由空气中电缆黑色表面的Z、E和g的常数值表[1]计算得到的散热系数，有外护层的电缆和有非金属表面的电缆应视为黑色表面，无外护层的电缆，如裸铅包或裸钢带电缆h值应为黑色表面h值得88%；Δθs为超过环境温度以上的电缆表皮温度，K。

(Δθs)1/4的计算如下：

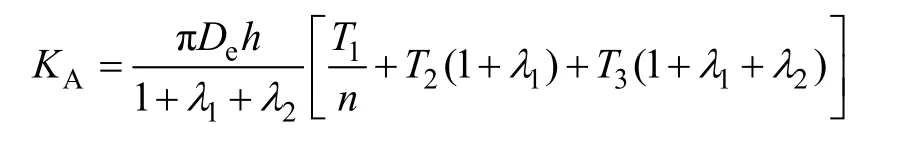
令(Δθs)1/4的初值为2，并反复迭代直至相邻两数值之差为

这是考虑绝缘损耗引起的温升，当介质损耗忽略时Δθd=0。式中，T1、T2与T3代表的是IEC标准算法中的相应热阻；λ1为电缆金属套损耗相对于导体总损耗的比例；λ2为电缆铠装损耗相对于导体总损耗的比例。

为了方便计算，对式（1）至式（7）进行积分处理，再借助Matlab软件可以得出暂态下的导体温度计算式为

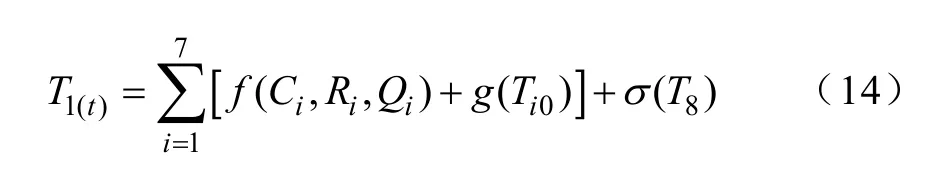
式中，f(Ci，Ri，Qi)为与电缆本体各层参数相关的量；g(Ti0)为暂态时电缆各层的初始温度；σ(T8)为实时的环境温度。经验证，电缆各层的初始温度对最终形成的稳态温度场影响较小，但与电缆导体温度到达稳态所需时间存在关联，本文重点在于温度计算，暂不讨论初始温度分布与到达稳态时间的关系。在电缆本体参数、电缆接地方式和排列方式固定的情况下，外界环境温度对导体初始温度分布和温升速率有决定性作用。

3 计算结果与分析

3.1 温度场计算结果

图3至图10是以电缆敷设在自由空气中为例，计算不同排列方式下电缆各层温度随时间变化的响应曲线即温度场分布；并以单端接地方式为例，计算两种情况下施加阶跃电流载荷时的各层温度随时间变化响应曲线。仿真计算中各参数取值和计算方法与IEC标准一致。另外，图中看起来只有5条曲线是因为T1基本被T2覆盖，T5基本被T6覆盖，即半导电层温度将导体层温度覆盖，铝护套层温度将缓冲层温度覆盖。覆盖的原因为两层基本紧贴且后层厚度很小，导致温度变化较小。

3.2 计算结果分析

图3、图5与图7的仿真计算结果是电缆各层温度随时间变化的响应曲线。敷设条件为在没有太阳直射、没有外部热源的自由恒温空气中；接地方式为双端接地，只计算皱纹铝护套的环流损耗，忽略涡流损耗；排列方式分别为3根平面排列相互之间不接触，导体间距为2De、3根平面排列相互接触、三角形排列相互接触；电流负荷为IEC标准计算的额定载流量；外界环境温度恒为40℃，电缆各层初始温度为40℃。

图3 施加IEC标准载流量电缆温度场变化

图4 施加IEC标准载流量电缆温度场变化

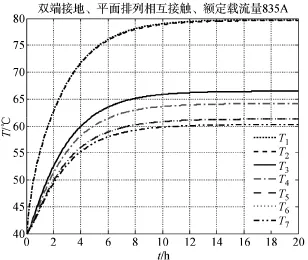
图5 施加IEC标准载流量电缆温度场变化

图6 施加IEC标准载流量电缆温度场变化

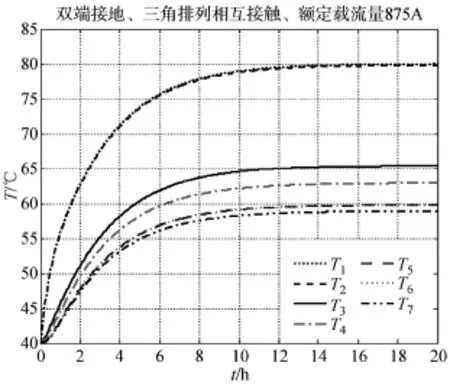
图7 施加IEC标准载流量电缆温度场变化

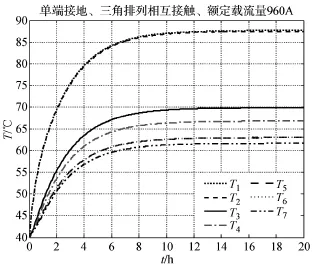
图8 施加IEC标准载流量电缆温度场变化

图9 施加阶跃电流电缆温度场变化

图10 施加阶跃电流电缆温度场变化

图4 、图6与图8的仿真计算结果同样是电缆各层温度随时间变化的响应曲线。接地方式为单端接地，只计算皱纹铝护套的涡流损耗，忽略环流损耗；敷设条件、排列方式、电流负荷与外界环境温度及各层初始温度同上文所述条件一致。

根据图3至图8仿真计算结果可以看出，在IEC标准载流量作用下，无论采用何种接地方式，电缆如何排列，电缆导体稳态温度都小于90℃。从仿真计算图中能明显看出，该方法能够得出不同电流负荷情况下电缆实时的温度场分布即电缆各层的实时温度值，同时利用该方法能够计算电缆导体达到稳态90℃所对应的载流量即实际载流量。

图9的仿真结果是在施加阶跃电流负荷情况下，电缆各层温度随时间变化的响应曲线。敷设方式为无日照无热源的自由空气，接地方式为单端接地，排列方式为三角形排列相互接触，外界环境温度恒为40℃，电缆各层初始温度为40℃，施加电流载荷为600A、800A、1000A、800A、600A、400A各12h。

图10的仿真计算结果同样是施加阶跃电流负荷情况下，电缆各层温度随时间变化的响应曲线。排列方式为平面排列相互不接触，导体间距2De，接地方式、外界环境温度、电缆各层初始温度分布与施加电流同图9所述条件一致。

根据图9、图10仿真计算结果可以看出，此方法能够预测施加阶跃电流后导体温度达到最大值所需时间，也可以推测施加阶跃电流后导体在一定时间内温度的上升值。

根据该计算方法可以计算得出，双端接地、平面排列导体间距2De的情况下，载流量为1060A。电缆导体温度从初始温度上升到稳态温度90℃所需时间为8.38h，电缆外皮达到稳态时的温度为60℃，所需时间为6.28h。同样条件下IEC标准载流量为860A，在该电流负荷作用下导体稳态温度为73℃。

1）在单端接地、平面排列导体间距2De的情况下，计算得出载流量为1105A，电缆导体温度从初始温度上升到稳态温度90℃所需时间为8.44h，电缆外皮达到稳态时的温度为58℃，所需时间为6.78h，同样条件下IEC标准载流量为1080A，在该电流负荷作用下导体稳态温度为87.7℃。

2）在双端接地、平面排列相互接触的情况下，计算得出载流量为939A，电缆导体从初始温度上升到稳态温度90℃所需时间为11.17h，外皮达到稳态时的温度为65℃，所需时间为10.89h，同样条件下IEC标准载流量为835A，在该电流负荷作用下导体稳态温度为79.8℃。

3）在单端接地、电缆平面排列相处接触的情况下，计算得出载流量为1017A，电缆导体温度从初始温度上升到稳态温度90℃所需时间为8.27h，电缆外皮达到稳态时的温度为60℃，所需时间为6.11h，同样条件下IEC标准载流量为950A，在该电流负荷作用下导体稳态温度为83.4℃。

4）在双端接地、电缆三角形排列相互接触的情况下，计算得出载流量为980A，电缆导体温度从初始温度上升到稳态温度90℃所需时间为11.67h，电缆外皮达到稳态时的温度为63℃，所需时间为10.61h，同样条件下IEC标准载流量为875A，在该电流作用下导体稳态温度为80℃。

5）在单端接地、电缆三角形排列相互接触的情况下，计算得出载流量为982A，电缆导体温度从初始温度上升到稳态温度90℃所需时间为10.78h，电缆外皮达到稳态时的温度为62℃，所需时间为7.72h，同样条件下IEC标准载流量为960A，在该电流作用下导体稳态温度为87.7℃。

为了更直观的反应计算结果，列表2、表3如下。

表2 3种方法不同情况下载流量值

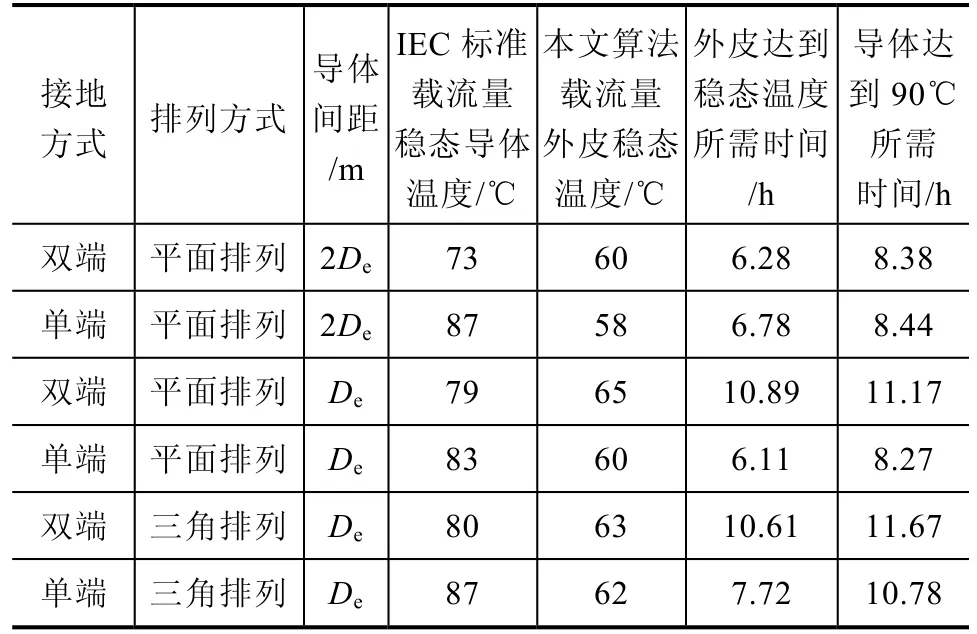
表3 IEC标准载流量导体稳态温度和本文算法载流量外皮稳态温度与导体和外皮达到稳态所需时间

4 结论

文献[16-20]对改进IEC算法做了大量的实验，将实验数据与理论计算值进行对比分析，得出利用改进IEC算法计算载流量误差很小，而本文方法理论计算值与改进IEC方法计算值基本一致，这就验证了方法的可靠性。利用本文采用的方法，可以对电缆表面温度数据和电缆导体温度数据进行实时计算，将计算结果与实验监测结果进行对比分析，得到电缆的可靠动态载流量。也可以预测在电流突变后，电缆表皮温度数据和电缆导体温度数据的动态变化范围，并推算达到最高允许温度所需时间，这对监测电缆运行状态有重要意义。

1）IEC 60287标准计算得到的额定载流量过于保守，并未充分利用电缆的性能，造成了资源的浪费，可以在保证安全的基础上适当提高载流量。

2）改进的IEC算法计算环境热阻时以环境温度、电缆表面温度和铝护套温度为计算依据，而本文环境热阻的计算以环境温度，敷设方式和电缆排列方式为依据，不需使用电缆外皮温度与铝护套温度的实时监测数据，与改进算法比较，在误差十分接近的情况下，减小了工作量；与IEC标准算法比较，大大提高了计算温度场的准确度。

3）本文方法计算导体与电缆外皮的实时温度准确可靠，可以作为在线监测的依据。根据该方法计算的实际载流量与达到固定温度所需要的时间，在实际应用中能够进行不同条件下载流量的预测，有助合理优化运行负荷。

[1] 马国栋. 电线电缆载流量[M]. 北京: 中国电力出版社, 2003.

[2] IEC 60287-1. Calculation of the Current Rating-Current Rating uations (100% Load Factor) and Calculation of Losses[S].2001

[3] IEC 60287-2. Calculation of the Current Rating-Thermal Resistance[S]. 2001.

[4] IEC 60287-3. Calculation of the Current Rating-Sections on Operating Conditions[S]. 1999.

[5] IEC 60853. Calculation of the Cyclic and Emergency Current Rating of Cables[S]. 1989.

[6] JB/T 10181. 电缆载流量计算[S]. 2014.

[7] 李志坚, 张东斐, 曹慧玲, 等. 地下埋设电缆温度场和载流量的数值计算[J]. 高电压技术, 2004, 30(增1): 27-28, 30.

[8] Nahman J, Tanaskovic M. Determination of the current carrying capacity of cables using the finite element method[J]. Electric Power Systems Research, 2002, 61(2): 109-117.

[9] 陈民铀, 张鹏, 彭卉. 应用无网格伽辽金法的电力电缆载流量计算[J]. 中国电机工程学报, 2010, 30(22): 85-91.

[10] 郑良华, 于建立, 周晓虎, 等. 直埋电缆群载流量和稳态温度场计算新方法[J]. 高电压技术, 2010, 36(11): 2833-2837.

[11] 杨泽亮, 候志云, 何杰. 封闭空间电缆群散热的数值模拟[J]. 华南理工大学学报: 自然科学版, 1998, 26(2): 59-65.

[12] 赵健康, 姜芸, 杨黎明, 等. 中低压交联电缆密集敷设载流量试验研究[J]. 高电压技术, 2005, 31(10): 55-58.

[13] 庄小亮, 余兆荣, 牛海清, 等. 日负荷系数与10kV XLPE电缆周期负荷载流量关系的试验研究[J]. 电力自动化设备, 2014, 34(4): 168-172.

[14] Yilmaz G, Karlik S E. A distributed optical fiber sensor for temperature detection in power cables[J]. Sensors and Actuators A-Physical, 2006, 125(2): 148-155.

[15] 张振鹏, 赵健康, 饶文彬, 等. 电缆分布式光纤测温系统测量结果符合性的比对试验[J]. 高电压技术, 2012, 38(6): 1362-1367.

[16] 雷成华, 刘刚. 高压单芯电缆动态增容的理论分析与实验研究[D]. 广州: 华南理工大学, 2012: 24-29.

[17] 刘刚, 周凡, 刘毅刚. 高压单芯电缆铝护套下热阻的动态特性与实验研究[J]. 高电压技术, 2013, 39(3): 712-718.

[18] 雷成华, 刘刚, 阮班义, 等. 根据导体温升特性实现高压单芯电缆动态增容的实验研究[J]. 高电压技术, 2012, 38(6): 1397-1402.

[19] 雷鸣, 刘刚, 赖育庭, 等. 采用Laplace方法的单芯电缆线芯温度动态计算[J]. 高电压技术, 2010, 36(5): 1150-1154.

[20] 刘刚, 阮班义, 林杰, 等. 架空导线动态增容的热路法稳态模型[J]. 高电压技术, 2013, 39(5): 1107-1113.

Real-time Conductor’s Temperature Calculation of High Voltage Cable and Prediction Probe of Ampacity

Zhao Baishan Wang Qingzhu
(School of Information Science and Engineering, Shenyang University of Tecnology, Shenyang 110870)

The real-time temperature of cable conductor is the foundation to judge whether the cable reaches its ampacity. In order to calculate the temperature field of cables, related researchers have used the methods of numerical analysis, analytical calculation, testing and temperature-line monitoring, etc. In this paper, on the basis of constructing the cable dynamic thermal circuit model, combined with the laying environment conditions, used Matlab software to get the numerical solution of differential equation groups of dynamic thermal circuit, obtained real-time distribution conditions of the temperature field of cables, and predicted withstand ampacities of cables under different conditions. According to the method, the real-time distribution conditions of temperature field of cables can be obtained under the action of applying the step current, as well as the required time that the conductor reaches the specified temperature can be calculated. The analysis results show that the method in this paper can calculate the real-time temperature field and the withstand ampacities of cables, as well as the temperature rise time of conductor can also be reasonably estimated. For the relevant project practice, the method has important reference significance.

high voltage cable; thermal circuit model; real-time temperature; predict ampacity

赵柏山（1980-），男，辽宁省沈阳市人，博士，副教授，主要从事嵌入式开发、电子与通信工程等方面的研究。