基于ADAMS的Stewart次镜平台运动学和动力学仿真

梁凤超， 黄 刚， 谭 爽， 康建兵， 林 喆， 康晓军

(北京空间机电研究所， 北京 100090)

基于ADAMS的Stewart次镜平台运动学和动力学仿真

梁凤超， 黄 刚， 谭 爽， 康建兵， 林 喆， 康晓军

(北京空间机电研究所， 北京 100090)

调整次镜位姿是空间相机提高成像质量的有效方法之一。为优化Stewart次镜调整平台的结构设计，研究了基于ADAMS虚拟样机技术的并联机构运动学和动力学仿真方法。首先对 Stewart 并联机构进行了运动学理论分析，建立了运动学逆解数学模型并计算了解析结果；然后，在ADAMS中建立了并联机构虚拟样机并进行运动学逆解仿真，其仿真结果与解析结果一致，证明了虚拟样机模型的正确性；再将ADAMS运动学逆解作为各杆驱动函数，实现了运动学正解及动力学逆解仿真。基于ADAMS虚拟样机技术的并联机构运动学和动力学特性分析方法，为次镜调整平台的结构优化设计提供了理论依据和主要参数。

并联机构； 运动学； 动力学； 虚拟样机； 次镜

0 引 言

在空间光学遥感器中，主镜和次镜的相对位置和姿态对于高质量成像有着重要影响。但空间相机受发射冲击、振动及在轨温度环境变化、应力释放等因素影响，可能会引起主次镜相对位置的误差及次镜倾斜，造成相机的成像质量下降。为保证主次镜光路的精确重合与对准，需要对次镜的位置与姿态做实时调整[1]。

现有的次镜的位姿调整方案主要包括以下3种：一是四翼梁式十字形中心支撑结构，通过调整螺钉实现五自由度的调整，精度为0.5 mm，满足不了高精度要求[2]；二是温正方等[3]设计的串联式五自由度次镜调整机构，结构较为简单，控制方便，但是存在误差累计，刚性小，动态性差，体积大等缺点；三是六自由度并联机构，意大利的VST望远镜系统中，次镜调整机构选用Stewart 并联六自由度机构[4]，具有高精度、高刚度、高稳定性和误差小、摩擦小、动态性能好等优点，但控制过程复杂。

并联机构是在精度、刚性和操作大负载能力方面具有良好性能的闭链机械，适用于高精度、大载荷的场合。并联机构的最早应用可以追溯到1938年，Pollard提出采用并联机构作为汽车喷漆装置。1948年，Gough等[5]在英国伯明翰的邓禄普橡胶公司研制出一种用于轮胎检测的六自由度并联机构，但直到1962年才出现相关文字报道。并联机构的构型有多种，当前应用比较广泛的 Stewart 平台的经典机构是由Stewart[6]于1965年提出的6-SPS(S-球铰链，P-运动副)并联结构，用作训练飞机驾驶员的飞行模拟器。1978年，澳大利亚著名机构学教授Hunt[7]提出将六自由度Stewart平台作为机器人的机构应用到工业机器人。1979年，McCallion等[8]首次设计出了在小型计算机控制下的精密装配中完成校准任务的并联机器人。

Stewart 平台机构包括上、下2个平台和6个可伸缩的驱动杆，动平台和驱动杆之间使用6个球铰或虎克铰连接，静平台和驱动杆使用6个虎克铰连接，这6根驱动杆都可以独立地自由伸缩。通过对6根驱动杆的协调控制，动平台可实现沿空间X、Y、Z轴的平移和绕X、Y、Z轴的转动共6个自由度的运动，从而实现位置和姿态的变化[9-10]。由于该结构平台能灵活地实现六自由度的三维空间运动，而且具有稳定性强、承载能力大、精度高、误差小、响应快等一系列的优点[11]。某型号空间相机采用Stewart构型的次镜调整平台，实现地面相机光学系统装调阶段的次镜组件位姿调整以及在轨后的次镜位姿调整。

并联机构是一个多输入、多输出系统，杆间耦合性强，容易产生奇异位形、灵活性差等缺点。为避免或减少上述缺点对机构性能的影响，须对并联机构进行结构优化设计，这就须要对并联机构的运动学和动力学进行仿真研究，为次镜调整平台的结构优化设计、制造和模拟运动提供理论依据和主要参数。

1 理论基础

并联机构的运动学分析是进行动力学分析、控制策略研究、结构优化设计的基础，因此建立准确的运动学模型对并联机构的研究至关重要。运动学分析是求解并联机构的输入与输出构件之间的位置、速度、加速度之间的关系。当已知并联机构的主动件的位置，求解并联机构的末端件的位姿，称为并联机构的运动学正解；反之，若已知并联机构末端件的位姿，求解并联机构的主动件的位置，称为并联机构的运动学反解[12]。

Stewart并联机构结构如图 1 所示，由上下两个平台和6个并联的、可独立自由伸缩的杆件组成，伸缩杆和平台之间通过虎克铰A1～A6和球铰B1～B6连接。下平台作为静平台，以伸缩杆的位移作为输入变量，则可以控制动平台(上平台)的空间位移和姿态。实际机构中通过改变6根可以伸缩的支杆长度来实现并联机构动平台的运动，即沿x、y、z轴的平移和绕动坐标系z、y、z轴的转动的欧拉角U、V、W。

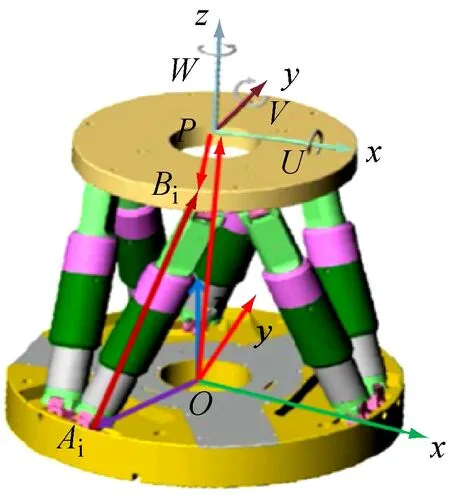
图1 Stewart并联机构坐标系

为了定量地表示动平台各处的坐标，在静平台的综合质心处建立惯性坐标系(静坐标系)O-xyz，坐标原点为O；在负载的综合质心处建立连体坐标系(动坐标系)P-xyz，坐标原点为P，各坐标系的方向如图1所示。上铰点旋转中心在连体坐标系中的坐标向量为Bi(B1,B2,B3,B4,B5,B6)，下铰点旋转中心在惯性坐标系中的坐标记为Ai(A1,A2,A3,A4,A5,A6)。坐标系确定之后，并联机构的运动平台的位姿用广义坐标向量q表示，其中q=[q1,q2,q3,q4,q5,q6]T, [q1,q2,q3]T表示运动平台中心在惯性坐标系中的坐标向量，[q4,q5,q6]T表示运动平台在惯性坐标系中的姿态角即欧拉角。这6个参数就确定了动平台的空间位姿。将欧拉定理中提到的刚体绕某一轴的有限转动分解为依一定顺序绕连体坐标轴的3 次有限转动，则每次转过的角度可定义为确定刚体转动前后相对位置的3个广义坐标[13]。按照不同的旋转顺序，可以有24 种旋转方式，本文选取绕x→y→z坐标轴的顺序旋转，如图2所示。

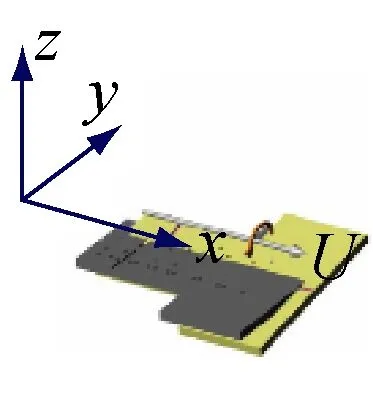
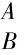
(1)

式中：cU= cosU, cV= cosV, cW= cosW, sU= sinU, sV= sinV, sW= sinW。动平台姿态广义坐标系q=[x,y,z,U,V,W]T时，各支杆的长度为

(2)

式中：li为图1所示支杆矢量AiBi，li为杆长，i=1, 2, …, 6。

2 Stewart并联机构参数化建模

建立虚拟样机模型和建立物理样机模型的道理相同，要尽量简化模型。在满足虚拟样机仿真运动的完整性的同时，应尽量减少模型的零件数。在最初的仿真分析建模时，不必过分追求构件几何形体的细节部分和实际一致，因为这往往要花费大量的建模时间，而此时的关键是能够顺利地通过仿真并获得初步结果。从程序的原理来看，只要虚拟样机模型的质量、质心、转动惯量等和实际构件相同，仿真结果与物理样机就是等价的。

ADAMS软件是集建模、求解、可视化技术于一体的虚拟样机软件[14]。通常用ADAMS软件建模时都是利用其自带的几何体模块建模，确定了几何体的各参数后几何体也随之确定，当几何体尺寸发生变化或需要分析参数对整个系统影响时，就需要手动修改参数，这样就大大增加了工作量。为了避免重复的工作，ADAMS提供了参数化建模功能，即将所建立模型的特征值都用ADAMS中的设计参数表示，这样, 模型就会随着设计参数的修改而自动改变。特别是在ADAMS中作参数分析时，对设计参数在设置区间内平均化，模型自动更新，ADAMS自动进行系列仿真，能够观察不同参数值下样机性能，大大简化了人工修改过程。

本文分析过程中的模型就是在ADAMS/View下建立的。将整个并联机构系统简化为静平台、动平台、6个支杆、6个球铰链和6个虎克铰链，将上铰点Bi(B1,B2,B3,B4,B5,B6)、下铰点Ai(A1,A2,A3,A4,A5,A6)及平台半径等设置为变量，参数化建模参数表及模型如图3所示。

3 运动学仿真

建完模型之后，ADAMS/Solver模块自动生成机械系统模型的动力学方程，提供静力学、运动学和动力学的解算结果。ADAMS/Postprocessor模块可以用来输出高性能的动画、各种数据曲线，还可以对曲线进行积分、求导、求和、求差等处理。应用这两个模块可以对并联机构的运动学和动力学进行仿真分析。

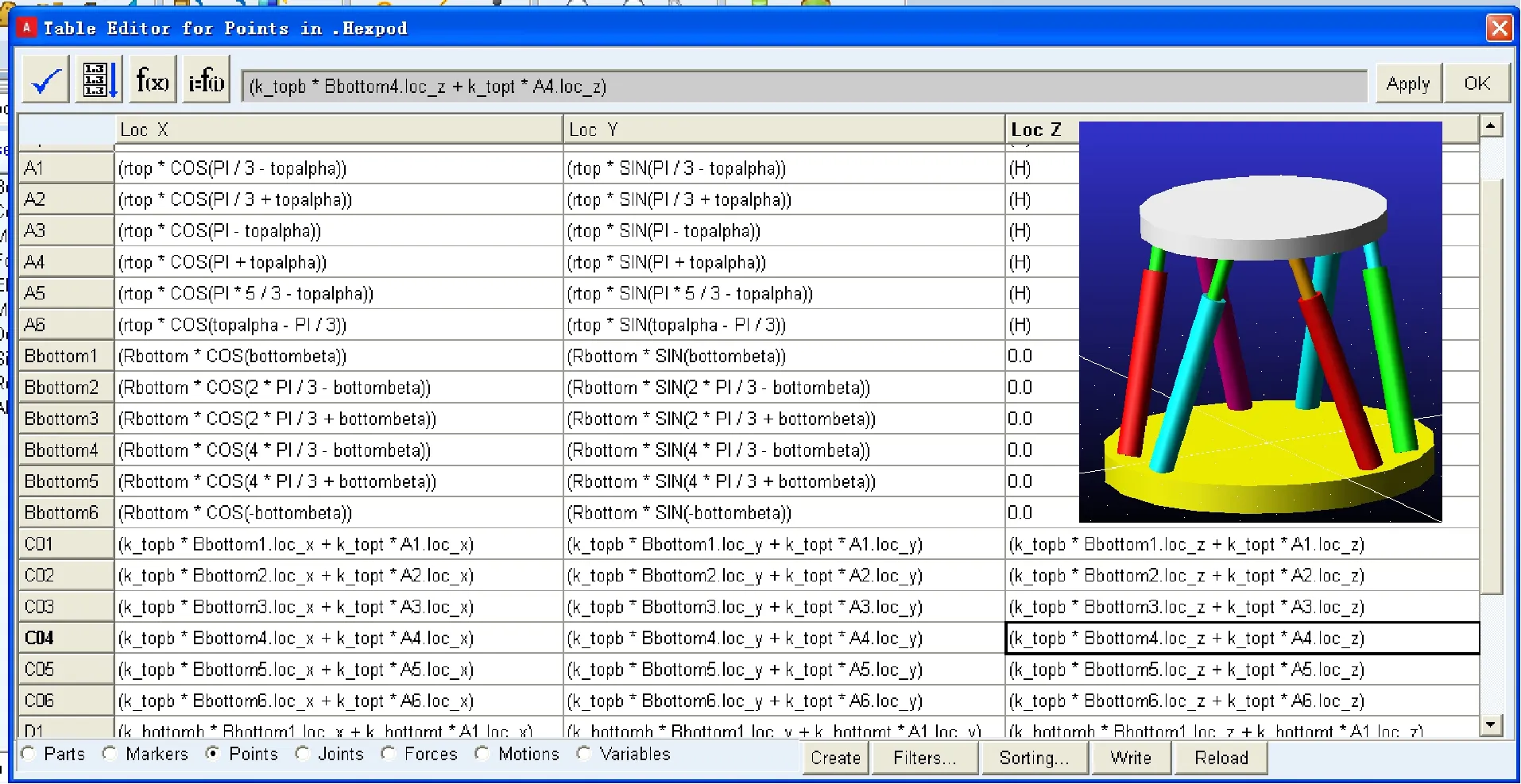
图3 Stewart并联机构参数表及虚拟样机

当并联机构的动平台以一定的形式运动时，其速度和加速度与各杆伸缩的速度和加速度有着严格的依赖关系，但驱动杆杆长和动平台位姿之间的关系是非线性的。从伺服控制的角度来说，动平台的运动空间为虚轴空间，而驱动关节空间为实轴空间。因此，在进行运动控制时，必须通过位置逆解模型，将实现给定的动平台位姿和速度信息变换为伺服系统各杆杆长的控制指令，从而驱动并联机构动平台实现期望的运动。

由于并联机构的运动学逆解容易而正解困难，一般设计并联机构时通过运动学逆解计算各支杆的行程、速度、加速度，从而使设计的并联机构能够满足需要的运动能力。动平台在运动范围内的运动，都是通过6根杆长的变化来使动平台中心到达运动范围内的任意位置。为了在ADAMS中实现并联机构虚拟样机动平台6个自由度的运动，在动平台中心处施加一般点运动激励来实现其运动仿真，使动平台实现沿x、y、z轴的移动以及沿x、y、z轴的旋转，以此来模拟动平台在实际工作中的一般运动。一般点运动驱动对话框如图4所示。 将驱动加在动平台中心点，即MARKER_79， 参考点选择静平台中心点MARKER_80，这样就保证了给定的运动指标的参照系是静坐标系。自由度驱动类型有位移、速度、加速度以及驱动函数。同时建立上、下铰点的位移测量，测量两点之间的距离，得到实时杆长曲线。

图4 在动平台中心点施加一般点运动驱动

为不失一般性，在动平台中心点处六自由度方向同时加载正弦位移/转角驱动函数，在ADAMS中仿真此驱动下的平台运动，再经后处理可得到6条支杆的长度变化曲线，此即为运动学逆解。加载驱动即动平台的规划轨迹函数见图4，x、y、z方向的位移函数设置为5sin(2pit)，是振幅为5 mm、f=1 Hz的正弦驱动信号；U、V、W旋转方向的驱动函数为5d·sin(2pit)，是振幅为5°，角频率为360°/s的角度驱动，其中的‘d’表示角度单位为(°)。

设定仿真时长为1 s，仿真步数为100 步，这样可以得到一个周期内各支杆的长度。仿真结果如图5所示。为了得出各支杆的变化量，先测出每一时刻各支杆的长度，然后通过长度值减去初始值而得到各支杆的伸缩量。

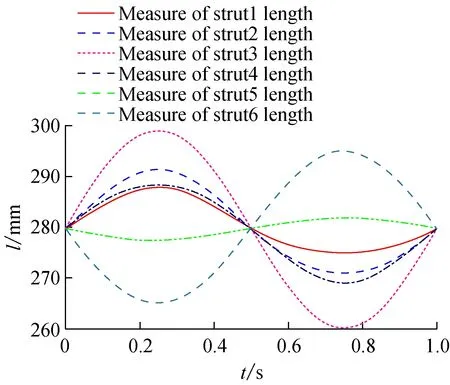
图5 ADAMS中运动学仿真得到的6支杆长度曲线

为了验证理论模型和ADAMS 模型的正确性，通过Matlab 编程，计算出了动平台x、y、z、U、V、W方向加载驱动函数5sin(2pit)时各支杆的实时长度。再将理论模型计算曲线与ADAMS虚拟样机模型仿真曲线在每个时刻上相减，得到图6所示的误差曲线，可见两种模型的6支杆的伸缩量误差维持在10-5mm量级，说明两种模型在同一时刻的伸缩量一致，理论模型和ADAMS虚拟样机模型是正确的。

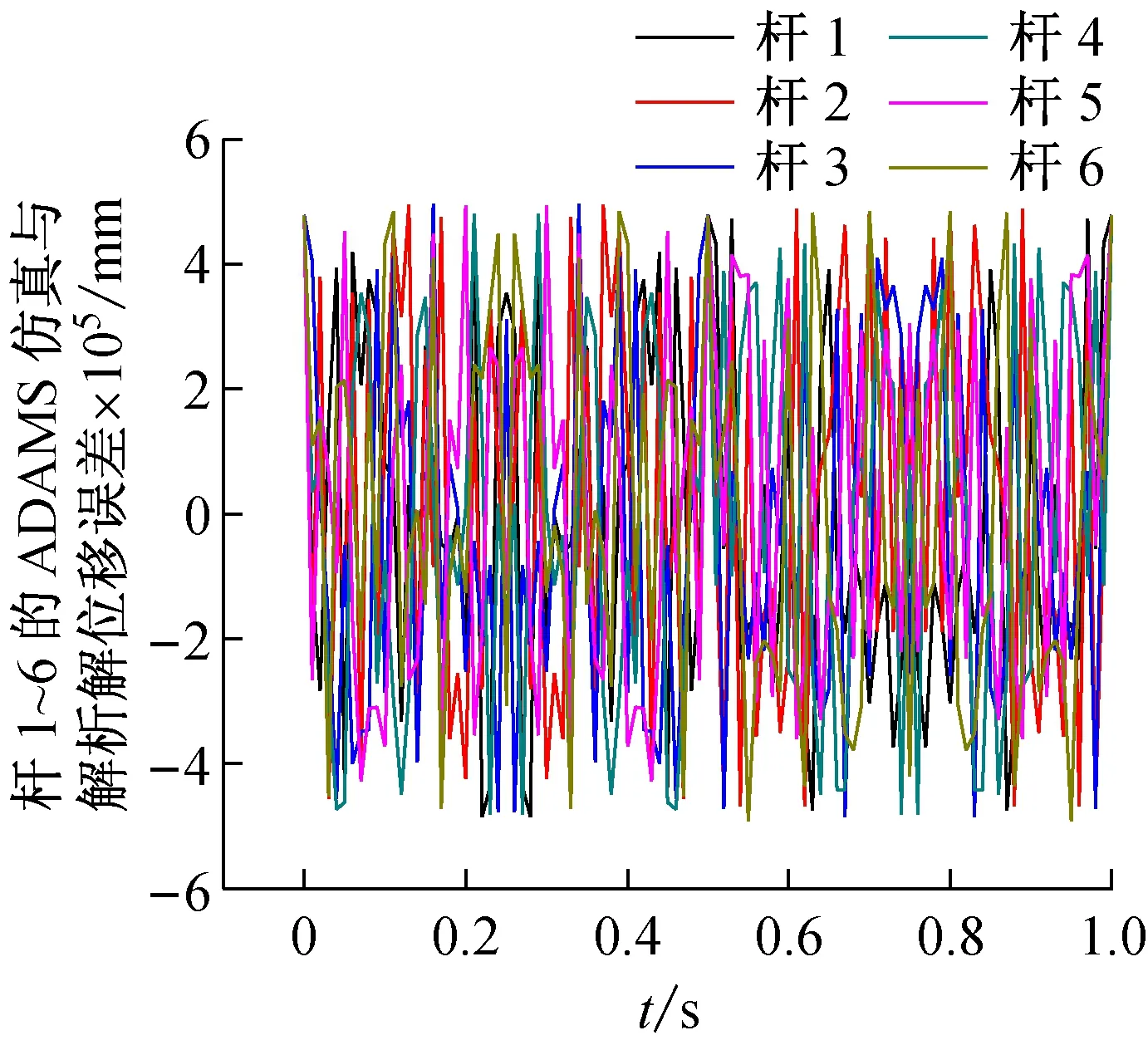
图6 并联机构6支杆长度仿真与计算误差

4 动力学仿真

对于给定的各关节连杆的驱动力或力矩，并联机构的位姿将发生什么变化，其运动的动态过程如何，不仅取决于其几何结构，而且还依赖于各关节连杆的惯性，即质量。对于并联机构，在一定载荷作用下，动平台实现某一运动时，各杆的驱动力也将随之变化。在整个运动过程中，各杆的驱动力变化是否平缓，力的大小是否符合要求，对于机构的设计、伺服执行元件的选择和实际的控制有着重要的意义。

并联机构的动力学研究包括机构的动力学建模、受力分析、惯性力计算、动力平衡、动力响应等方面，在六自由度并联机构的设计与控制中起到非常重要的作用，是确定并联机构主要结构参数的基础。由于并联机构的复杂性，其动力学模型通常是一个多自由度、多变量、高度非线性、多参数耦合的复杂系统。利用ADAMS仿真并联机构动力学时，ADAMS会根据机械系统模型，自动建立系统的拉格朗日运动方程，对每个刚体，列出6个广义坐标带乘子的拉格朗日方程及相应的约束方程，并自动求解，不需用户编程计算。许勇等[15]通过ADAMS对一种扭摆下行被动移动装置进行了动力学仿真验证，设计制作了原理样机并进行测试。

做动力学分析时需要知道并联机构动平台在任意位姿时各支杆的出力，可通过对并联机构做运动学正解得到支杆出力。利用ADAMS模型运动学逆解仿真结果可得到支杆1～6对应的样条函数：SPLINE_1～SPLINE_6。样条函数SPLINE_1如图7所示，第1列是各仿真点的时间，第2列为对应的伸长量。这样就知道了每个仿真时刻所对应的各支杆伸长量。再将ADAMS模型的动平台点对点驱动去除，在每条支杆的移动副关节处加上平移驱动MOTION_1～MOTION_6，设定驱动函数为AKISPL(time，0，SPLINE_1，0)，…，AKISPL(time，0， SPLINE_6，0)，这样就可以保证每个仿真时间点各支杆伸长量与反解时一致。为了验证在正解时动平台确实是做x、y、z、U、V、W向的正弦运动，需测量动平台在x、y、z方向的位移曲线及动平台的姿态角U、V、W。同时测量每个驱动所受的力，则可得到动平台做运动时每个杆的出力。最后，对仿真时间设置，由于用的是反解的样条线型数据，故仿真时间设置为1.0 s，仿真步数为100步。设置完成后对模型进行仿真，得到图8所示的动平台位姿曲线。可见，ADAMS中6支杆加载SPINE1～ SPINE6位移驱动，动平台的位姿正解曲线与求反解时加载在动平台上的6维驱动一致。

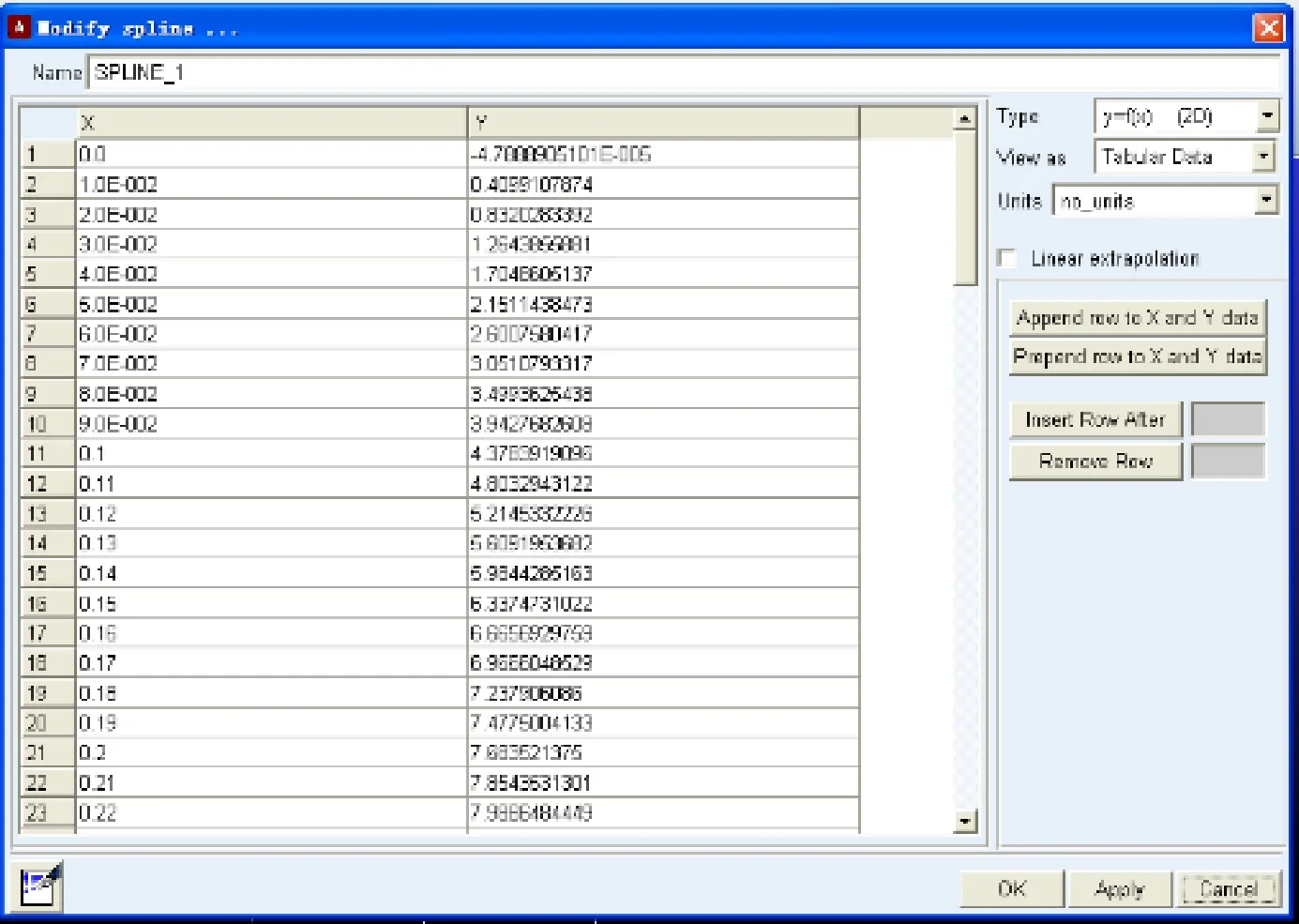
图7 支杆1伸长量SPLINE_1数据

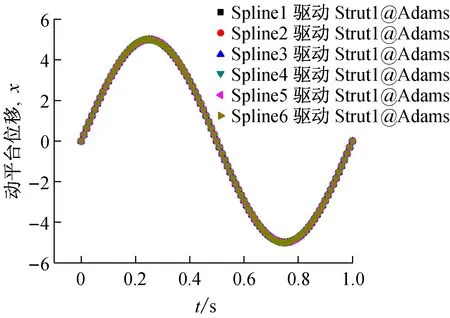
图8 动平台位姿轨迹

ADAMS模型中6条支杆加载SPINE1～SPINE6位移驱动、动平台外负载力为0 N时，6条支杆的驱动力曲线如图9所示。观察图9中的曲线可知，当动平台沿六自由度方向均为正弦运动规律时，每个支杆所受的力不相同。杆6所出的力最大，最大值达到16.6 N；杆4出力最小，其最大值为10.1N。

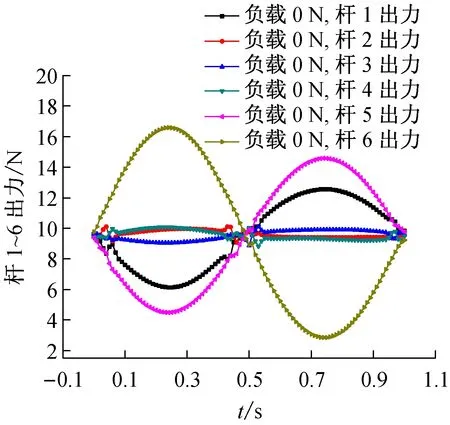
图9 动平台负载为0 N时6条支杆驱动力曲线

利用ADAMS中的添加力选项给动平台质心添加一个固定在动平台质心的常力，设负载力沿Z轴负方向，大小为500 N，则可测得动平台6个自由度运动规律均为5sin(2pit)时，6条支杆出力如图10所示：杆6所出的力最大，最大值达到129.9 N；杆3出力最小，其最大值为93.6 N。在判定各杆的最大出力后，即可根据此数值判定并联机构的负载能力，还可以据此选用各作动杆的驱动执行元件。从图9、10中可见，当并联机构平台没有外力作用时，作动杆的力用来克服自身重力，随着动平台的运动而变化，添加外力后，受力曲线整体上升，即杆的出力增加但运动曲线没有变化。

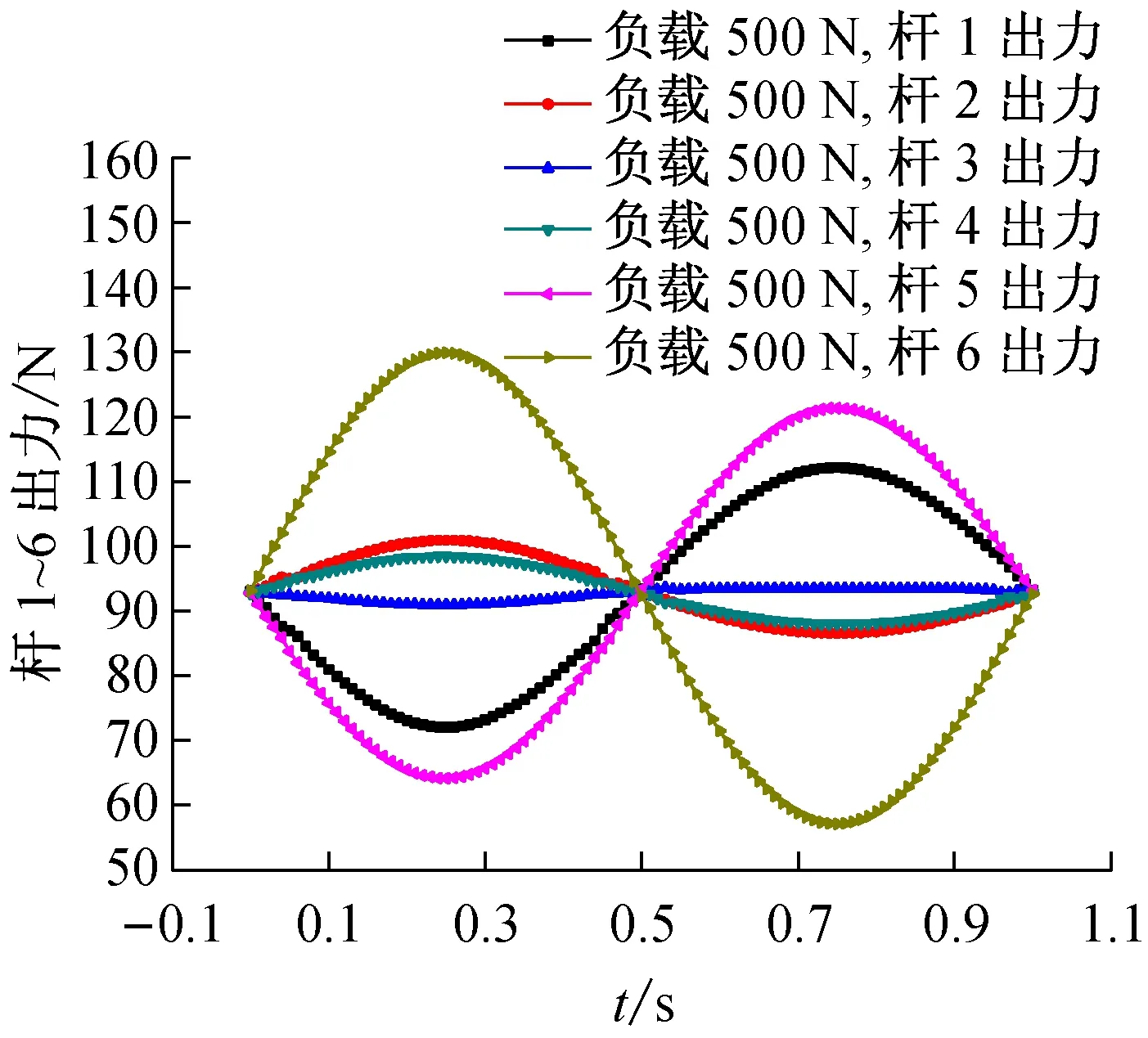
图10 动平台负载为500 N时6条支杆驱动力曲线

5 结 语

并联机构运动学、动力学仿真分析是Stewart平台结构优化设计、伺服元件选型及实现控制的基础。并联机构运动学和动力学分析多采用的是解析法，但其数学建模困难灵活性差、动平台工作空间复杂、空间运动很难直观想象，需要建立适当的模型并进行仿真。本文使用CAE仿真软件ADAMS来对并联机构的运动和动力性能进行分析，这种方法与理论建模的解析方法相比，具有参数化建模灵活、无繁杂理论公式推导及计算、运动模拟可视化等优势，为Stewart次镜调整平台的研究提供了一种新方法。

[1] 谭 爽. 空间光学遥感器次镜六自由度精密控制方法研究[D]. 北京：中国空间技术研究院工学硕士学位论文, 2015.

[2] 王富国,张景旭,杨 飞，等.四翼梁式次镜支撑结构的研究[J]. 光子学报， 2009, 38(3):674-676.

[3] 温正方, 张景旭, 张丽敏. 五自由度次镜调整机构的研究[J]. 工程设计学报， 2010, 17(6): 473-478.

[4] Schipani P, Perrotta F, Molfese C,etal. The VST secondary mirror support system[J]. Advanced Optical and Mechanical Technologies in Telescopes and Instrumentation pt.3., 2008(6)：23-28.

[5] Gough V E, Whitehall S G. Universal tyre test machine[C]∥Proceedings of the 9thInternational Technical Congress F.I.S.I.T.A, May 1962:117.

[6] Stewart D. A Platform with six degrees of freedom[C]∥Proceedings of International Mechanical, Engineering, London: 1965, 180(15): 370-386.

[7] Hunt K H. Kinematic geometry of mechanisms[M]. Oxford, Clarendon Press, 1978.

[8] McCallion H, Truong P D. The analysis of six-degree-of-freedom work station for mechanism assembly[C]∥Proceedings of the Fifth World Congress on Theory of Machines and Mechnisms,1979:611-616.

[9] 葛耀峥，程 佳，陶国良. 并联6自由度电动实验教学平台[J] . 实验室研究与探索，2012, 31(5): 34-36.

[10] 唐晓强，尹文生，孟明辰，等. 可重构并联实验装置设计与实验教学初探[J]. 实验室研究与探索，2005, 24(12): 11-13.

[11] Kong Xianwen. Type synthesis of parallel mechanisms[M]. Springer Berlin Heidelberg, 2007:1-4 .

[12] Merlet J P. Parallel Robots[M]. 2nd. Netherland: Springer Science & Business Media, 2006: 66-74.

[13] John J Craig. Introduction to Robotics Mechanics and Control[M]. Prentice Hall, 2005: 28-41.

[14] 赵玉侠，狄杰建，高德文. 基于ADAMS的微型管道机器人三维实体运动仿真[J]. 实验室研究与探索，2011, 30(1): 26-29.

[15] 许 勇， 王春燕， 王义灿，等. 扭摆下行被动移动装置的动力学建模及参数仿真[J].实验室研究与探索，2015, 34(10): 116-120.

Simulation of Kinematics and Dynamics of Stewart Platform for Secondary Mirror Based on ADAMS

LIANGFengchao,HUANGGang,TANShuang,KANGJianbing，LINZhe,KANGXiaojun

(Beijing Institute of Space Mechanics & Electricity, Beijing 100090, China)

Posture adjustment of the secondary mirror is one of the effective ways to improve the image quality of space camera. In order to optimize the structural design of Stewart platform for secondary mirror posture adjustment, simulation method of kinematics and dynamics of parallel manipulator based on ADAMS virtual prototyping technology was studied. First, theory analysis of inverse kinematics of Stewart parallel manipulator was performed, and the analytical results of inverse kinematics were obtained via mathematical modeling and calculating. Then, inverse kinematics simulation was carried out in ADAMS after the virtual prototype of parallel manipulator was established. The simulation results in ADAMS and analysis results were consistent, hence it proved the correctness of the virtual prototype model. Then, the kinematics and inverse dynamics simulation were realized by using result of inverse kinematics in ADAMS as drive function of each strut. The analysis method of kinematics and dynamics of parallel manipulator, based on ADAMS virtual prototyping technology, provided a theoretical basis and the main parameters for optimizing design of secondary mirror.

parallel manipulator; kinematics; dynamics; virtual prototyping; secondary mirror

2016-05-09

梁凤超(1978-)，男，吉林松原人，博士，高级工程师，研究方向为并联机构控制技术。

Tel.：010-68114781; E-mail: fc.liang@qq.com

TH 113.2

A

1006-7167(2017)02-0107-05