偏心轮推杆行星传动的参数优化及其软件设计

张 淳， 范浪层

(陕西科技大学 机电工程学院， 陕西 西安 710021)

偏心轮推杆行星传动的参数优化及其软件设计

张 淳， 范浪层

(陕西科技大学 机电工程学院， 陕西 西安 710021)

内齿圈是偏心轮推杆行星传动机构的关键部件.为了降低机构的质量，并提高其传动性能，需对其机构的系统特征参数进行优化.本文将内齿圈体积的最小值作为目标函数，以顶切限制、强度限制、最佳受力条件等作为约束条件建立数学模型，并使用C#编程语言，采用外点惩罚函数法设计出了一款专门用于其参数优化计算的软件.最后通过软件进行了实例计算.从计算的结果可以看出偏心距e，内、外滚柱半径R1、推杆长度L尺寸都有所减小，且内齿圈的体积有很大程度的降低，从113 298.4 mm3降为36 682.52 mm3.因此，该优化方法达到了优化的目的，且使该传动机构的结构更加紧凑了.

偏心轮推杆行星传动； 参数优化； C#程序设计

0 引言

偏心轮推杆行星传动是一种新型的活齿传动，活齿传动最初的结构方案早在20世纪30年代就己经提出[1].此后，国内外先后进行研制并改进成多种形式的活齿传动机构.其中，国内比较典型的有套筒活齿少齿差传动装置[2]、“滚珠活齿传动”[3]、摆动活齿减速机[4]、凸轮活齿行星传动装置[5]；在国外，由前苏联推出了“正弦滚道滚珠传动”[6]，且生产的正弦滚珠减速器成功用于石油钻探中，美国提出了“无齿齿轮传动”[7].

偏心轮推杆行星传动是由陶栋材教授提出的一种新型推杆活齿传动[6]，具有较大范围的传动比、体积小、质量轻、效率高、过载能力大、运转平稳和结构紧凑等特点[8-10]，可广泛应用于农业、轻工业、纺织业、化工业、矿山等轻重型机械设备中.偏心轮推杆行星传动的结构尺寸对其传动性能有很大影响，但依靠传统的经验计算方法很难使其性能达到理想的状态.

曲继方[11]对活齿传动理论进行了深入的研究，提出了推杆活齿传动结构尺寸的经验计算公式；阳林等[12]以最大重合度为优化目标得出了多组偏心轮和偏心距(R1，e)参数对，再以最小压力角为优化目标得出了最佳的(R1，e)参数对，以此实现了对推杆活齿减速机的部分参数的优化；段海燕[13]则使用平均啮合效率的最大值为目标函数对偏心轮推杆行星传动的参数进行优化，但因偏心轮推杆行星传动的结构和传动形式的限制，其效率仅提高了2%.

因此，为进一步提高产品设计的质量和发挥其潜在性能，本文将以内齿圈体积最小为目标函数，建立偏心轮推杆行星传动参数优化的数学模型，并设计一款专门用于其参数优化的软件.

1 确定系统特征参数的计算方法

1.1 系统特征参数的提取

偏心轮推杆行星传动的结构主要由5个部分组成，分别是：偏心轮、传动圈、内齿圈、推杆及活齿滚柱.其基本结构如图1所示，其传动原理详见文献[8].

图1 偏心轮推杆行星传动的基本结构简图

由偏心轮推杆行星传动的基本结构简图可以看出，齿形较为复杂的内齿圈是偏心轮推杆行星传动的关键部件，其齿廓曲线也决定了传动性能的好坏，内齿圈理论齿廓曲线的极坐标方程为[6]：

(1)

式(1)中：x1,y1—分别为偏心点到外滚柱圆心的距离在x轴和y轴上的投影，L—推杆长度，e—偏心轮的偏心距，Z—内齿圈齿数，α—推杆沿逆时针方向转动的角度，R—偏心轮半径，R1—内、外滚柱半径，各参数的直观表达参照图2.

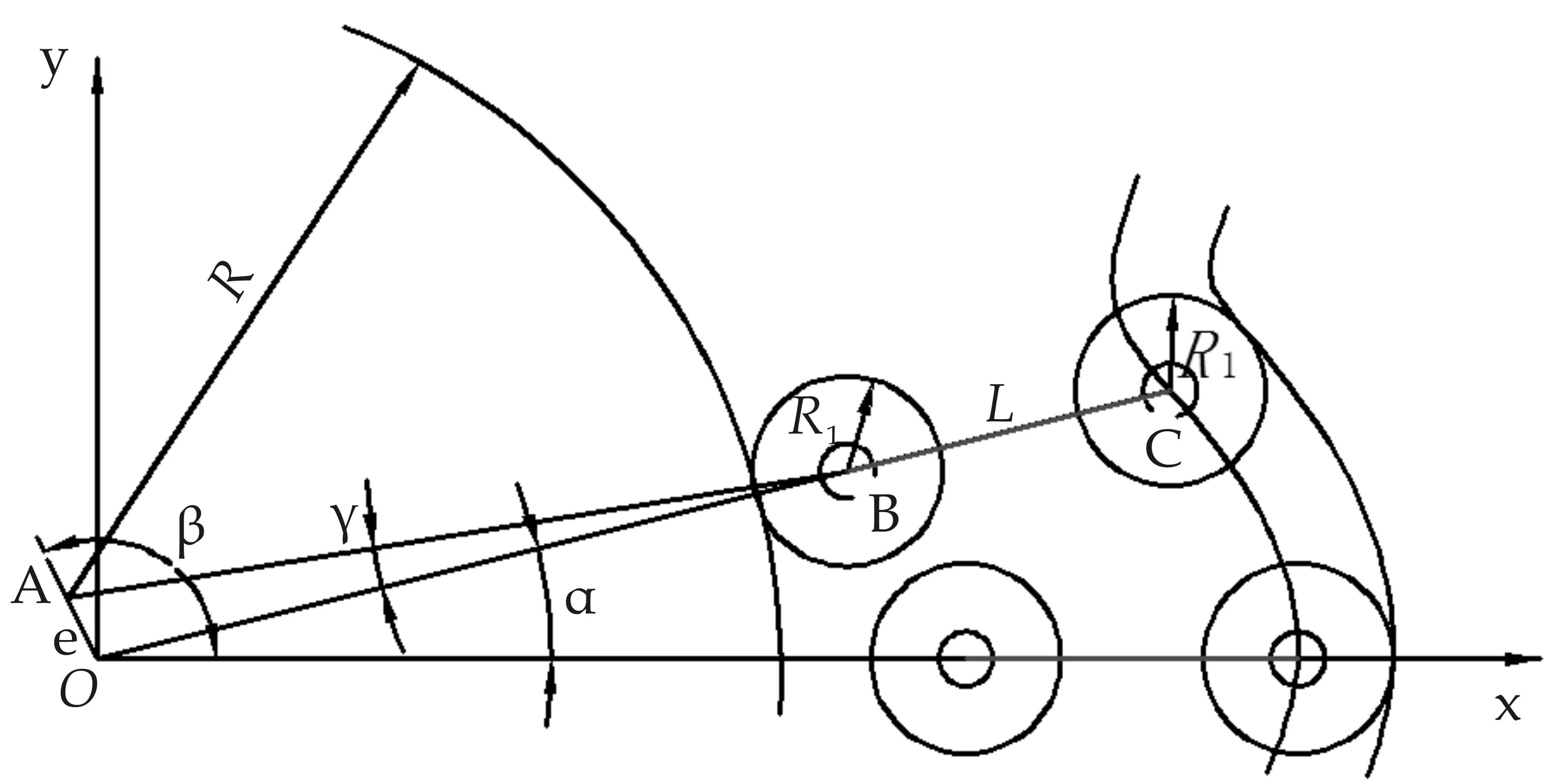
图2 偏心轮推杆行星传动的齿廓方程图

内齿圈实际齿廓曲线为距理论齿廓曲线R1的径向等距曲线，其曲线方程表达式为[14]：

(2)

从内齿圈的齿廓曲线方程可知，可将偏心轮半径R，偏心轮的偏心距e，内、外滚柱半径R1，推杆长度L和内齿圈齿数Z这5个参数作为系统特征参数.

1.2 确定系统特征参数的计算方法

确定偏心轮推杆行星传动特征参数的方法是根据偏心轮推杆行星传动的输入功率P、输入轴转速n和传动比i，由相关公式算出R、e、R1、L和Z这5个特征参数的值，具体计算方法如下：

(1)求传递力矩

Tv=(9.545×103/n)P·i·η·%

(3)

式(3)中：η—传动效率，%.

(2)确定偏心轮半径R

(4)

式(4)中：K1—传动比系数，一般取K1=9～11，传动比大取小值.

(3)确定滚柱半径R1

(5)

式(5)中：K2—重合度系数，一般取K2=0.6～0.7，重合度大取小值.

(4)确定偏心距e

(5)确定推杆长度L

一般取L=(3～5)R1，可根据用户要求和偏心轮推杆行星传动的结构尺寸确定.

(6)确定内齿圈齿数Z

当内齿圈固定，偏心轮输入，传动圈输出时：Z=i-1；当传动圈固定，偏心轮输入，内齿圈输出时：Z=-i，负号表示内齿圈与偏心轮的输入方向相反.

经上述方法初步确定了偏心轮推杆行星传动的系统特征参数，根据已有的经验，这些参数的值并不能使机构的性能达到最优，因此有必要对这些参数加以优化，以便更好的满足工程实际的需求.

2 系统特征参数的优化

在实际应用中，我们通常希望机构能以较小的尺寸获得较高的性能，因此需对偏心轮推杆行星传动的特征参数进行优化，本文以体积最小为目标函数，以顶切限制、强度限制、最佳受力条件等作为约束条件建立数学模型.

2.1 建立目标函数

在给定功率、转速和传动比的条件下，为使偏心轮推杆行星传动的结构紧凑，降低成本，把偏心轮推杆行星传动体积的最小值作为优化设计的目标函数，而内齿圈是其关键部件，故将内齿圈体积的最小值作为目标函数，其体积的粗略计算公式为：

(6)

式(6)中：R外—内齿圈外轮廓圆半径，R外=R+2R1+L+3e，mm；R内—内齿圈齿顶所在圆的半径，R内=R+2R1+L-e，mm；B—内齿圈的宽度，本文取B=4e，mm.

2.2 约束条件

2.2.1 顶切的限制

内齿圈齿廓的曲率半径对传动的性能有很大影响.要保证不发生顶切，需使内齿圈齿廓曲线的曲率半径大于滚柱半径.设内齿圈齿廓曲线的最小曲率半径为ρmin，则不产生顶切的条件是[6]：

(7)

2.2.2 强度的限制

(1)偏心轮与内滚柱啮合副接触的强度条件为：

(8)

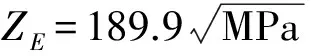
(2)内齿圈与外滚柱啮合副接触的强度条件是：

(9)

式(9)中：σQ—内齿圈与外滚柱接触的接触应力，MPa；[σ]H2—内齿圈与外滚柱的许用接触应力，MPa；FQ—内齿圈与外滚柱接触的法向压力，N；ρQ—内齿圈与外滚柱接触点处的当量曲率半径，mm.

当推杆移动副双面接触时，

(10)

当推杆移动副单面接触时，

(11)

(12)

式(12)中：ρ0—内齿圈齿廓与活齿外滚柱接触点处的曲率半径，mm.

2.2.3 最佳受力条件

推杆活齿在传动过程中受到偏心轮对活齿内滚柱的正压力FP、内齿圈对活齿外滚柱的正压力FQ以及传动圈导槽对推杆两边的力F1、F2,为了便于分析，将内外滚柱和推杆固化成一个活齿单元来进行受力分析，受力分析如图3所示.

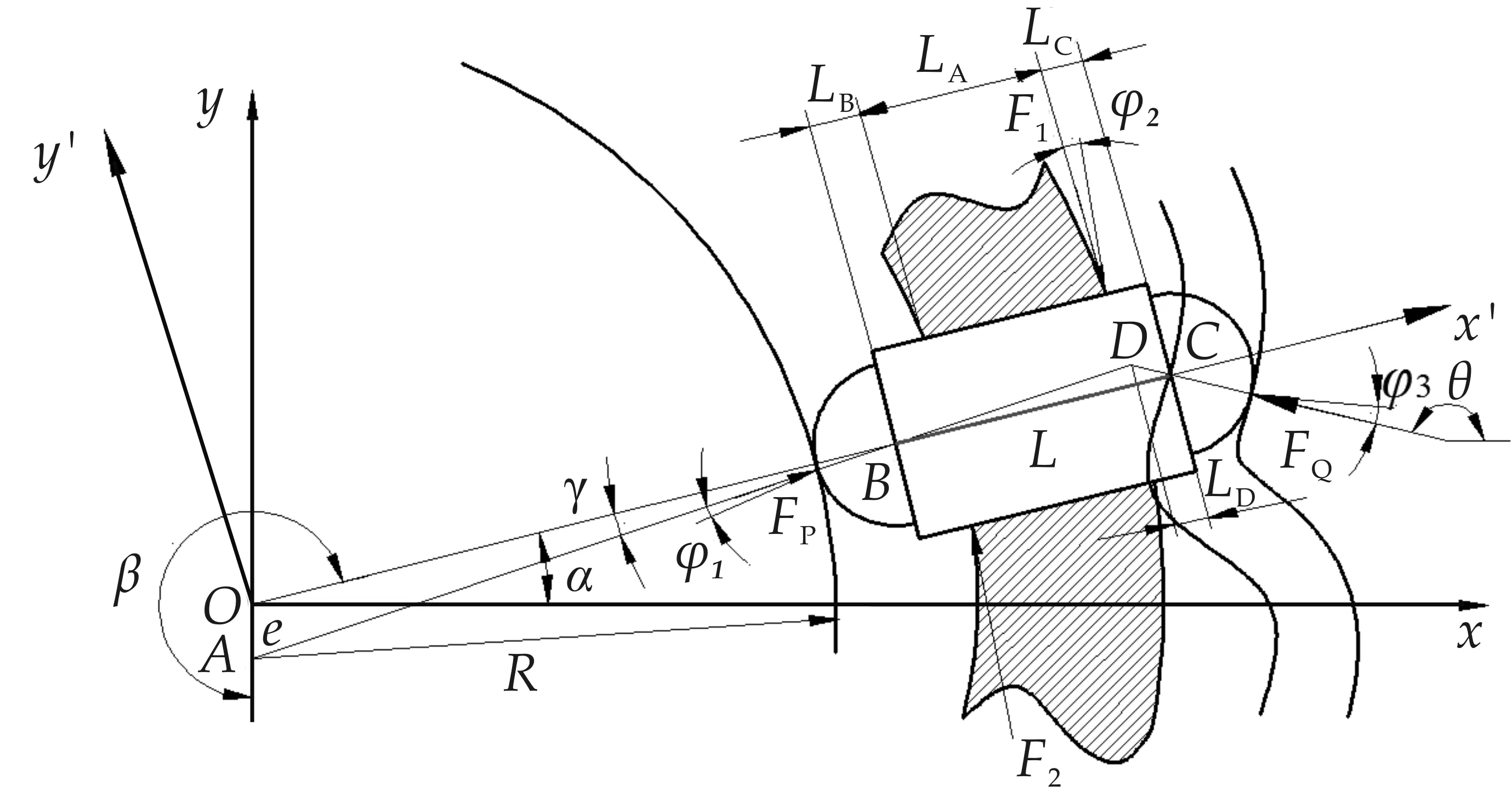
图3 推杆活齿受力分析

建立局部坐标系x′Oy′，x′的方向为OC方向，由此可得到推杆活齿受力在局部坐标系x′Oy′上的平衡方程如下所示：

(13)

方程(13)略去第三式中较小的二、四两项解得：

FQ=

(14)

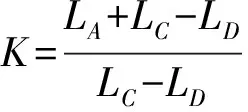
由上面的关系可以看出，在外载荷FQ固定不变时，尺度系数K越大则所需要的驱动力FP就越小，因此在满足传动性能的前提下应该尽量增大尺度系数K.由尺度系数公式可知，增大LA、LD和减小LC这三种途径都可使尺度系数K有所增加，但LA和LD的增加势必造成推杆的长度L也随之增长，从而加大了机构的径向尺寸，这显然是不可行的，所以需减小LC来增大尺度系数K.外伸长度LA与推杆活齿所处的位置有关，分别在工作开始和结束时取得最小值和最大值，即：

(15)

式(15)中：M—内齿圈齿顶与传动圈外圆间的径向距离，一般取1～2 mm[12]，可将LCmax减小至0，从而得R1=2e+M，这就是推杆活齿受力的最佳条件.

2.3 建立优化模型

由于偏心轮推杆行星传动内齿圈的齿数Z可由传动比直接求出，因此只对偏心轮半径R，偏心轮的偏心距e，内、外滚柱半径R1，推杆长度L这四个参数进行优化，并分别用x1、x2、x3、x4来表示，建立的数学模型为：

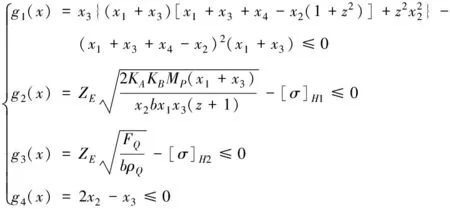
3 优化软件的设计及优化实例

3.1 优化软件的设计

根据建立的数学模型，使用外点惩罚函数法结合C#编程语言设计一款专用于偏心轮推杆行星传动参数优化的简易软件，软件部分程序代码如下：

usingSystem;

usingSystem.Collections.Generic;

usingSystem.Linq;

usingSystem.Text;

usingSystem.Threading.Tasks;

……

publicdoublembhanshu(double[]x)

{

doublef;

doublepi=

3.1415926535987932;

f=32*pi*x[1]*x[1]*(x[0]

+x[1]+2*x[2]+x[3]);

returnf;

}

……

publicdouble[]sumt(double[]x,doubleh,

doubleebsin,intyw)

{

inti,k,a,b,c;

doublefact,f,mc;

double[]x0=newdouble[N];

double[]xy=newdouble[5];

mc=MC;

ywddf(yw);

f=xfout(x,0);

k=1;

do

{

for(i=0;i

x0[i]=x[i];

baowr(refx,h,ebsin,yw);

f=xfout(x,k);

fact=0.0;

for(i=0;i

fact+=(x[i]-x0[i])*(x[i]-x0[i]);

fact=Math.Sqrt(fact);

k++;

mr*=mc;

}

while(fact>ebsin);

for(a=0,b=0,c=0;a<5;

a++)

{

if(b<4)

xy[a]=x[b++];

else

xy[a]=f;

}

returnxy;

}

软件的界面如图4所示.

图4 偏心轮推杆行星传动的参数优化软件界面

3.2 参数优化的实例

已知一偏心轮推杆行星传动的基本参数为：额定功率P=3 KW，输入转速为n=1 500 r/min，传动比i=16，输出为同向，试确定其基本结构参数.

将基本参数代入公式计算后，定出偏心轮半径R=50 mm，偏心轮的偏心距e=3.5 mm，内、外滚柱半径R1=7 mm，推杆长度L=24.5 mm，内齿圈齿数Z=15.将这几个基本结构参数值输入软件，然后点击优化按钮，得出优化结果如图5所示.

图5 偏心轮推杆行星传动基本结构参数优化结果

4 结论

根据最后实例验证的结构可以得到如下结论：

(1)已知额定功率P、输入转速n和传动比i，按照系统特征参数的计算方法计算出的几个特征参数的值是合理的，由此证明了该计算方法的可行性.

(2)通过软件的优化结果可以看出，软件在优化过程中对偏心轮的偏心距e，内、外滚柱半径R1，推杆长度L等进行了调整，且尺寸都有所减小，并且内齿圈体积有很大幅度的减小.结合相关的理论知识发现，优化后的结构参数使偏心轮推杆行星传动的结构更加的紧凑了，不仅节省了机构的材料，降低了机构的质量，还提高了偏心轮推杆行星传动的传动性能，使其能更好的应用在复杂的工况中.

[1] 周有强，胡茂弘，张文照.少齿差传动的发展概况[J].齿轮，1983,67(11):24-27.

[2] 周有强.套筒活齿少齿差传动装置[P].中国专利：CN8720-9455，1988-02-17.

[3] 李瑰贤，杨伟君，顾晓华.滚柱活齿传动受力分析的研究[J].机械设计，2002，20(1)：18-20.

[4] 曲继方.摆动活齿减速机[P].中国专利：CN90222527,1991-04-24.

[5] 陈兵奎.凸轮活齿行星传动装置[P].中国专利：CN9911472-9，1999-09-08.

[6] 陶栋材.偏心轮推杆行星传动设计理论[M].北京：机械工业出版社,2010.

[7] 李勇进，刘金伟，刘 刚.活齿传动分类方法及结构改进新思路的探索[J].机械,2007，34(9)：70-73.

[8] 陶栋材,高英武,全腊珍,等.偏心轮推杆行星传动的传动原理研究[J].湖南农业大学学报(自然科学版)，2000，26(4):314-317.

[9] 陶栋材，卢月娥，尹 红，等.偏心轮推杆行星传动内齿圈及其结构特性研究[J].农业工程学报,2000,16(6)：18-21.

[10] 李瑰贤,杨伟君,顾晓华.滚柱活齿传动的啮合理论及齿廓接触数值仿真[J].哈尔滨理工大学学报,2001,6(4)：28-31.

[11] 曲继方.活齿传动理论[M].北京：机械工业出版社,1993.

[12] 阳 林,吴黎明,李定华.推杆活齿减速机系统特征参数优化与CAD/CAM[J].机电工程,1998(3):9-12.

[13] 段海燕.偏心轮推杆行星传动优化设计及动力学仿真研究[D].长沙:湖南农业大学,2010.

[14] 徐芝纶.弹性力学[M].北京:高等教育出版社,1982.

【责任编辑：蒋亚儒】

The parameter optimization and software design of eccentric wheel handspike planetary transmission

ZHANG Chun， FAN Lang-ceng

(College of Mechanical and Electrical Engineering, Shaanxi University of Science & Technology, Xi′an 710021, China)

The ring gear is the key part of eccentric wheel handspike planetary transmission mechanism.To reduce the quality of the mechanism and improve it′s transmission performance, the system parameters′ optimization of the mechanism is necessary.A mathematical model for optimal design,whose objective function is the minimum volume of ring gear and constraint conditions are end cutting limit,the strength limit and the best stress condition,has been setted up.Based on C# programming language,a software which adopted outer point penalty function method and dedicated to parameter optimization calculation was designed.At last,an example calculation has been done through the software.As can be seen from the calculation results that the size of eccentricitye,internal and external roller radiusR1and push rod lengthLwere reduced,and the volume of ring gear had greatly reduced which fells from 113 298.4 mm3to 36 682.52 mm3.So the optimized method has been achieved the goal of the optimization,and the transmission mechanism of the structure is more compact.

eccentric wheel handspike planetary transmission; parameter optimization; C# programming design

2017-01-13 基金项目：陕西省科技厅科技计划项目(2014K07-08)

张 淳(1957-)，男，陕西西安人，教授，硕士，研究方向：机械设计理论、机械传动系统

1000-5811(2017)02-0142-05

TH132

A