遥感数据最小距离分类的几种算法

马 铭,苟长龙

(甘肃交通职业技术学院，甘肃 兰州 730070))

测绘4.0：拓普康索佳应用方案专栏

遥感数据最小距离分类的几种算法

马 铭,苟长龙

(甘肃交通职业技术学院，甘肃 兰州 730070))

近年来，遥感数据的应用在广度和深度上不断融合发展和拓展。遥感数据的分类已成为遥感地理信息系统的一门关键技术。快速、高精度的遥感图像分类算法是目前实用、先进的技术，也是研究的热点之一。传统的分类器包括：最大似然分类、最小距离分类、平行算法分类。新分类器包括：模糊分类、空间结构纹理分类、神经网络分类、决策树分类、专家系统分类。本文拟对最小距离分类的算法进行分析和概括。

1 传统最小距离分类

最小距离是一种传统的分类方法，其原理是根据待分类点到各类样本训练向量中心的距离，将其纳入距离最小的一类。通常对n个波段m个类别采用欧氏距离对其分类

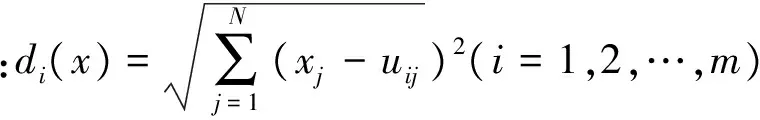
2 自适应最小距离分类

根据多维模式空间中的连续点集可以用多维球体的并集来逼近，通常采用集合细分方法K- means算法，每次分解为两个子集，以二叉树进行。每一类生成一棵二叉树，二叉树的一个节点对应一个球体，记录每个球体的球心及半径，球心定义为该节点上样本子集的中心，半径为该节点上的样本点到球心的欧氏距离的最大值。

自适应最小距离分类的基本原理是将每一个类模式点集近似为一组球体的并集，对待分类点判断其落在哪个球体，并赋予对应的类编号。首先求得所有模式集合的球体中心半径参数。自适应最小距离集合划分是一个由上而下、逐步细化的过程，即先用半径大的球体逼近，再用半径小的球体逼近，逐步进行细化直到达到相应的分类精度为止。根据对样本分类的精度要求自适应地控制样本集合的分解过程，就可以使不同类的小球尽可能分离，从而提高精度。

2.1 自适应距离最小分类的基本步骤

求出该点到各类对应的子集树的距离D，待分类点P到子集树T的距离D(T,p)定义为：

(1) 如果P到T的根节点对应的球心欧氏距离d大于该节点球体的半径的两倍，则忽略该节点细分得到的所有小球，并令D=d。

(2) 如果T的根节点已经是叶节点，则令D=d。

(3) 若步骤(1)、(2)均不满足，则D递归定义为P到T的左右子树T1、T2的距离D1、D2的最小者，即：D1=D(T1,P)，D2=D(T2,P)；D=min(D1,D2)。

根据最小距离原理，将距离D最小的一子集树的类号赋予待分类点。

2.2 自适应最小距离分类器的训练步骤

(1) 初始化各个类的子集树为只有一个根节点的情况，即根节点上的样本点集均为训练样本集合中属于该类的子集，同时求出各个根节点上样本点集的中心和半径。

(2) 对各个子集树进行训练，对各个叶节点，如果按照前述分类算法对该节点上的样本点集进行细分，即生成其左右子节点，将样本点集用K- means分类算法分解为两个子集，分别作为两个子节点的样本点集，并求出左右子节点对应球体的中心和半径等参数。

(3) 重复步骤(2)对各子集树依次进行训练，直到没有一个子集树被更新，训练结束后，各个节点上的样本集合已经没有必要保留。

自适应最小距离分类用一组球体的中心来定义距离，较单个中心更准确，由于样本的集合分解是在对样本分类试验的反馈指导下自适应进行的，因此这一算法能有效地提高分类精度。

2.3 分类试验结果

本文试验所用的原始图像是葡萄牙里斯本地区泰吉河流域遥感图像，原始图像为256×256像素，6个波段,地面采样得到的样本为14类,共8046点。14类样本中包含土地、水和当地若干典型植被。笔者从8046点样本中随机选取2500点作训练样本集,然后对8046点采样样本进行分类,以便统计分类精度,得到的试验数据见表1，对全图进行分类的结果图像如图1所示。

图1 对全图进行分类的结果

分类算法正确点数正确率/(%)自适应最小距离分类747892．5传统最小距离分类326040．4

从表1中可以看出，自适应最小距离分类的精度要远远超过传统最小距离分类的精度。因此，它是一种有效的监督分类的算法，对训练样本作适当分解处理是提高有监督分类精度的有效方法。

3 加权最小距离分类

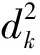
3.1 多重限制分类器

多重限制分类器将多重特征空间的每一条轴线分割,每一个类的分割区间基于其在该轴上的最大和最小值。该分类器的准确性依赖于每类数据统计后对最大值和最小值的选择。多重限制分类器简单、易理解，与其他分类器相比计算时间最短。但是该算法的准确性低,尤其在特征空间的分布中倾斜轴存在协方程和依赖时。执行该算法前,应使用主要成分分析作正交化。借鉴多重限制分类器,加权最小距离分类器为(Xi-Uki)2增加权值Vki。在训练过程中统计每类每个属性的最大最小值,在分类过程中如果待分类数据元组X的属性i的值超出第k类属性i的最大最小值范围,Vki取一个较大的值,其他情况Vki=1。Vki权值的大小通过试验确定。针对不同的数据集,权值的最优解不同,因此只能通过试验确定一个模糊最优值，结果为n(属性个数)。

3.2 标称型和字符串型属性

传统的最小距离分类器使用欧氏距离和马哈利诺贝斯距离时,无法处理有标称型和字符串型属性的数据。为了处理该类数据,需要特别定义标称型和字符串型属性的标准值。若属性i是标称型或字符串型属性,中心向量UK的属性值UKi取该类的所有数据元组中属性i的最频繁值。定义标称型和字符串型属性i的标准值,UKi的标准值定为0,与UKi相等的属性值为0,不等的为1。当第k类属性i的方差δki为0,即第k类该属性的值都相同时,待分类数据X的属性i的值Xi是否与UKi相等可能决定了其是否属于第k类,或与其他属性相比对分类有较大的贡献;当方差δki不为0时,Xi对决定X是否属于第k类,很可能贡献不大。因此为(Xi-Uki)2增加权值Wki,当δki≠0时,Wki=1;当δki=0时,Wki=100。Wki的值通过试验确定。针对不同的数据集,Wki的最优解不同,通过试验确定了一个模糊最优值100。

3.3 属性的方差

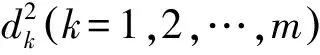
(1) 标准化欧氏距离

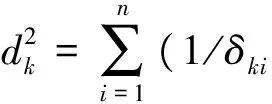
式中，δki是第k类属性i的方差。

(2) 标准化欧氏距离的一种变形

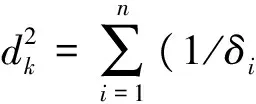
式中，δi是整个训练集的属性i的方差。

(3) 标准欧氏距离的另一种变形

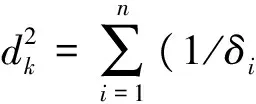
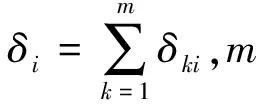
算法的步骤如下：

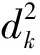
(2) 判定Xi与之距离最近的类，则属于该类。

3.4 试验结果

(1) 试验的结果主要是将传统最小距离与加权最小距离的性能作比较。

(2) 试验数据选自UCI资源集。表2列出了试验1使用的每个数据集的实例个数、类个数、属性个数等数据信息。由于传统的最小距离算法不能处理标称型数值数据，因此对于某些分类的试验结果没有列出。

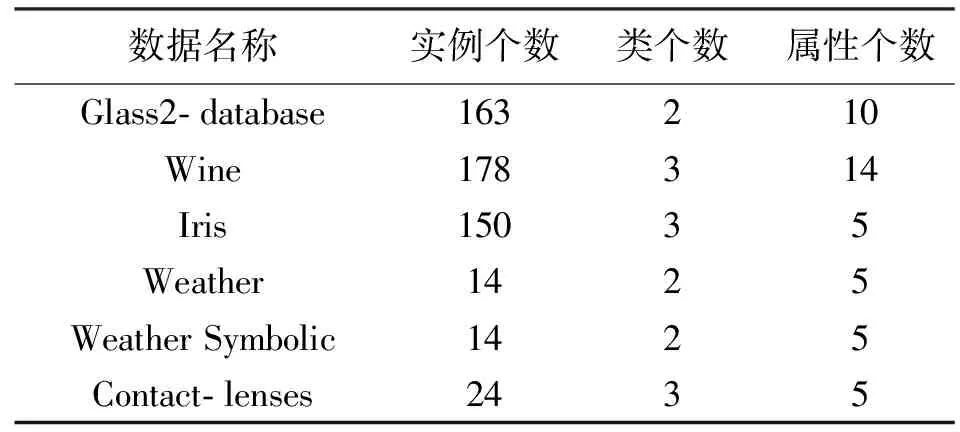
表2 试验1数据集的构成描述

试验的主要目的是将传统最小距离分类与加权最小距离分类在各数据集上的分类正确率进行比较。每个分类器的分类正确率是在测试集上成功预测的实例占总实例的百分比，采用10重交叉验证估计分类器的正确率。

两个分类器在每个数据集上分别测试了10次，每次试验采用不同的10重划分。表3列出了10次测试的平均正确率，并且列出了正确率的平均值。可以看出加权最小距离分类的正确率比传统最小距离分类的正确率高出了近8个百分点。

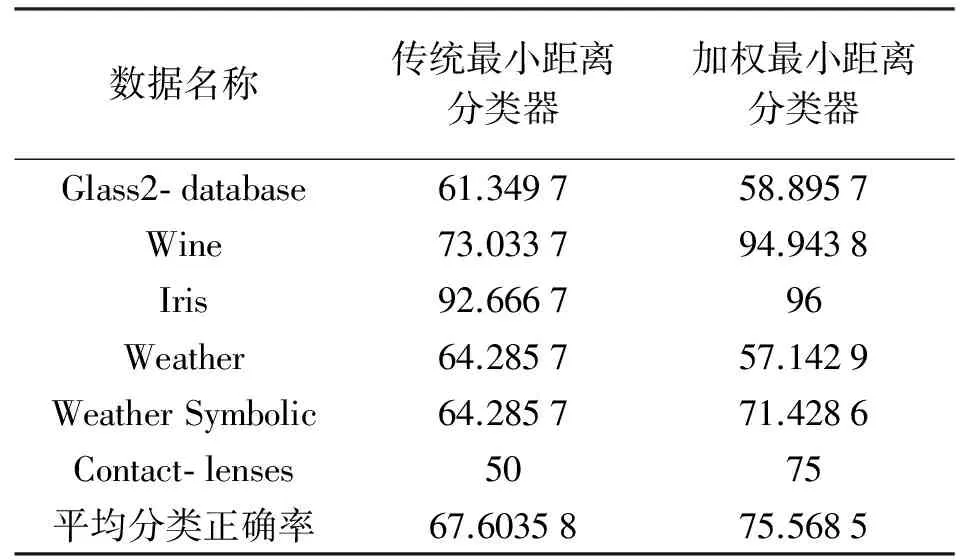
表3 两种最小距离分类器的试验结果 (%)

4 结 语

目前，由于遥感和GIS的紧密结合，对遥感数据的质量评价也越来越高。本文对遥感数据的分类作了一个简要说明。现对遥感数据分类补充如下：

(1) 本文对传统分类及其他两种改进方法作了比较，通过数据分析比较可得出加权最小距离分类是一种更有效的方法。

(2) 可以根据具体的精度要求进行选择性分类。

(3) 对加权最小距离分类和自适应最小距离分类精度的比较，将是下一个要研究的课题。