基于惯性导航系统的轨道检查仪双位置对准方法

张新春，崔希民

(中国矿业大学地球科学与测绘工程学院，北京 100083)

基于惯性导航系统的轨道检查仪双位置对准方法

张新春，崔希民

(中国矿业大学地球科学与测绘工程学院，北京 100083)

为提高轨道检查仪惯性导航系统对准精度，提出适用于轨道检查仪的惯性导航系统双位置对准方法。该方法利用轨道检查仪掉头方式，实现惯导系统加速度计常值零偏补偿。选用0.1°/h光纤陀螺仪和200 μg石英挠性加速度计组成惯性导航系统，在一铁路路段进行轨道检测试验。试验结果表明，双位置对准方法能够有效去除惯性器件零偏误差导致的轨道参数检测误差，在轨检仪连续工作300 m的情况下，铁路轨道水平检测精度明显提高。

惯性导航系统；轨道检查仪；双位置对准

近年来我国铁路交通事业迅速发展，普通铁路线路提速，高速铁路大量建设，铁路运输能力不断提升。铁路轨道线路平顺性是限制列车运行速度的重要因素。铁路线路不平顺轻则影响车辆运行速度，降低车辆工作寿命，重则引发恶性交通事故，危及行车安全，因此铁路轨道平顺性要求非常严格[1]。基于惯性导航系统的轨道检查仪可以精确测量铁路轨道的内部参数。初始对准用于确定惯性导航系统初始姿态，是惯性导航系统进行导航解算的必要初始条件，初始对准的精度直接影响导航解算精度[2- 4]，从而直接影响轨道参数测量精度。在初始对准方法中，最常采用的是直接对准，而对于轨道检查仪等高精度检测仪器，粗对准难以满足精度要求，精对准难以满足时间要求，从而需要一种短时、高精度的对准方法。多位置对准包含双位置对准、四位置对准等对准方法[5- 6]，对准精度高、速度快。多位置对准的优点是通过惯导系统的姿态转动，实现对陀螺及加速度计常值零偏的补偿。本文提出了适用于轨道检查仪的双位置对准方法，该方法利用轨道检查仪180°掉头模式，检测并修正水平加速度常值零偏，提高轨道检查仪水平检测精度。

1 轨道几何状态惯性检测系统

1.1 绝对轨道几何状态检测仪

绝对轨道几何状态检测仪以高精度机器人型全站仪、倾斜传感器和里程传感器为核心数据采集器，通过与CPIII控制网数据联测，得到轨道的轨距、轨向、高低、水平、扭曲等平顺性指标，同时可计算出轨道平面、高程与设计值的偏差。该类仪器测量精度高，但是测量方法复杂，每次测量均需要精密调节和自由设站定向，作业效率较低[7- 8]。

1.2 轨道几何状态惯性检测系统

基于惯性导航技术的轨道几何检测系统，在国内大型轨检车上已有成熟的应用，但其对惯性器件精度有较高要求，系统成本相对较高。因此，将惯性导航系统与现有轨道几何状态检测仪载体相结合，研制适用于我国高速铁路的低成本、高精度、高效率的新型轨道几何状态惯性检测系统是未来的发展趋势[9- 10]。系统的关键技术为惯性器件误差建模与补偿、多传感器信息融合及开发用于铁路检测的惯性测量平台。尤其选择合适的零速姿态修正方法，既能保证较长时间的惯导精度，又能保证载体的机动性能。

2 双位置对准原理

2.1 坐标系定义[11- 12]

2.1.1 载体坐标系(简称b系)

轨道检查仪载体坐标系O-XbYbZb，原点为车体结构中心点O，Yb轴沿轨道检查仪纵轴，指向运动方向，Xb轴沿轨道检查仪横轴向右，Zb轴垂直Xb轴和Yb轴，并构成右手直角坐标系。

2.1.2 地理坐标系(简称n系)

东北天地理坐标系O-XnYnZn，原点为载体质心，Xn轴和Yn轴在当地水平面内，分别指向东向和北向，Zn轴沿当地垂线指向天。地理坐标系随载体一起运动，且坐标轴指向始终保持原有的确定指向。

2.2 初始对准原理

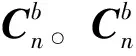
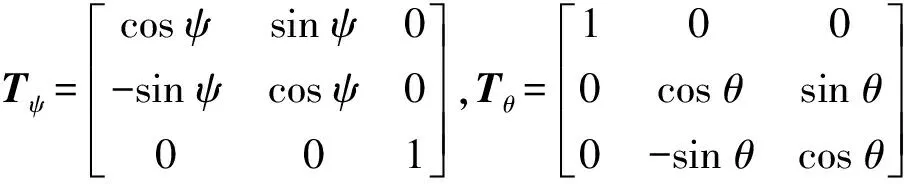
(1)

由Tψ、Tθ和Tγ可得

(2)

重力加速度g在载体系的投影关系[15]为

(3)

式中，ab=[axayaz]T为重力加速度在b系X、Y和Z轴加速度计上的投影；gn=[00g]，g为当地重力加速度。

将式(2)带入式(3)得到

ax=-sinγcosθg

(4)

ay=sinθg

(5)

从而得到俯仰角及横滚角解算公式

(6)

(7)

地球自转在b系陀螺仪投影关系式为

(8)

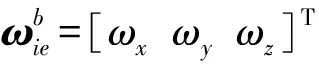
将式(2)带入式(8)得到Y轴陀螺投影分量公式为

(9)

根据式(9)解算得到航向角

(10)

根据式(6)、式(7)和式(10)得到航向角、俯仰角和横滚角计算公式，继而依据主值区间即可得到具体的航向角、俯仰角及横滚角，并根据式(2)解算得到姿态转换矩阵。

2.3 双位置对准原理

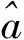
(11)

(12)

对于轨道检查仪掉头180°，因为轨道的轨向及高低不平顺，导致掉头过程中产生航向角偏差Δψ、俯仰角偏差Δθ和横滚角偏差Δγ[19- 20]。180°掉头的姿态转换矩阵为

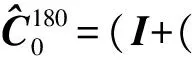
(13)

式中ψt=180°，从而计算式(13)得到

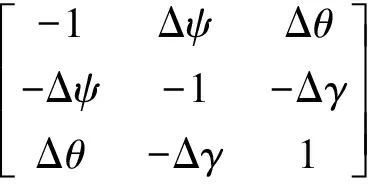
(14)

180°掉头加速度计敏感地球重力加速度值为

(15)

对于正常轨道线路，高低、轨向误差为小量，从而引起的航向角、俯仰角及横滚角误差均为小量，从而式(15)可以简化为

(16)

从而水平向X、Y轴加速度计常值偏置为

(17)

3 轨道检测试验

选用0.1°光纤陀螺仪和200 μg石英挠性加速度计组成惯性导航系统，惯性器件主要性能指标见表1。

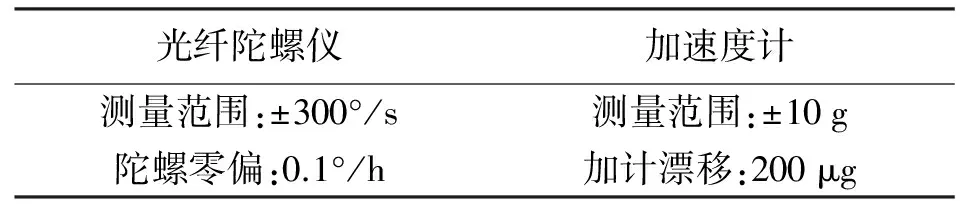
表1 惯性器件主要性能指标

轨道检测试验在北京某铁路测试场地进行，流程如下：轨道检查仪双位置对准，随后按照预定路线进行轨道检测，测量距离300 m。参考基准选用安伯格GRP1000型轨道检查仪，其精度指标见表2。

表2 GRP1000主要性能指标

采用双位置对准及普通粗对准的方式进行处理，得到轨道水平测量结果，如图1所示，从图中看出普通粗对准模式较双位置对准模式存在明显的水平值的常值偏差。以GRP1000型轨道检查仪测量数据为基准，得到双位置对准及普通粗对准解算精度，见表3，测量精度结果验证了双位置对准方法的正确性和有效性。

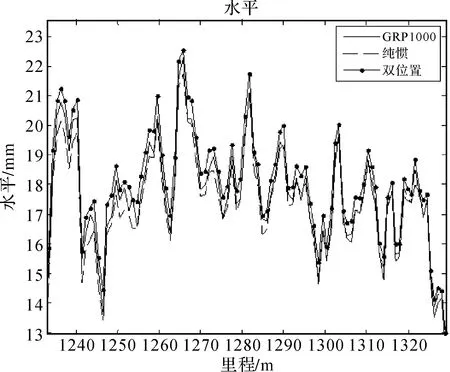
图1 水平结果对比

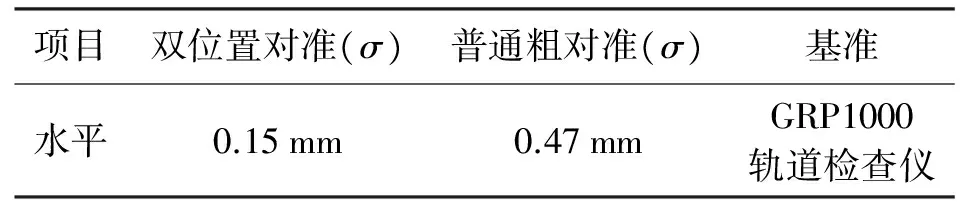
表3 轨道检测精度

4 结 语

轨道检查仪利用惯性导航系统双位置对准方法消除水平加速度计的常值零偏，降低了水平加速度计常值零偏对水平精度的影响，提高了轨道检查仪检测精度。在300 m的轨道检测距离内，采用双位置对准技术能够有效提高轨道检测精度，该技术对于提高轨道检查仪轨道检测精度具有实际意义。

[1] 贾瑞珍，金宗斌.高速铁路线路轨道平顺性问题的探讨[J].华东交通大学学报，1997，14(3):45- 48.

[2] FANG J C,WAN D J.A Fast Initial Alignment Method for Strapdown Inertial Navigation System on Stationary Base[J].IEEE Transactions on Aerospace and Electronic Systems, 1996,32(4):1501- 1504.

[3] LÜ Shaolin, XIE Ling,CHEN Jiabin.New Techniques for Initial Alignment of Strapdown Inertial Navigation System[J].Journal of the Franklin Institute,2009,346(10):1021- 1037.

[4] KIM K,CHAN G P.A New Initial Alignment Algorithm for Strapdown Inertial Navigation System Using Sensor Output[J].IFAC Proceedings Volumes,2008,41(2):13034- 13039.

[5] MATSUYAMA S,FUJIIA M,YAMAUCHIA K.Simulation Study of Four- mirror Alignment of Advanced Kirkpatrick- Baez Optics[J].Nuclear Instruments and Methods in Physics Research,2010,616(2- 3):241- 245.

[6] 芦佳振，张春熹，魏莹莹.挠性捷联惯组的多位置对准技术[J].系统工程与电子技术，2012,34(3)：562- 567.

[7] 钟昊然.轨道几何状态测量仪检测方法研究[D].成都：西南交通大学，2013.

[8] 袁玫.高速铁路轨道几何状态测量仪设计关键技术研究[J].铁道勘察，2012,38(5):10- 12.

[9] 蔡军.基于光纤陀螺仪的轨道方向不平顺检测系统的研究[D].南昌：南昌大学,2007:1- 4.

[10] 左玉良.轨道几何状态检测技术的应用研究[D].上海：同济大学，2007.

[11] FANG Jiancheng,GONG Xiaolin.Predictive Iterated Kalman Filter for INS/GPS Integration and Its Application to SAR Motion Compensation[J].IEEE Transactions on Instrumentation and Measurement,2010,59(4):909- 915.

[12] 韩晨，程军，杨秀英.地理坐标系浅析[J].价值工程，2012,31(32):318- 320.

[13] 以光衢.惯性导航原理[M].北京:航空工业出版社,1987.

[14] 秦永元，张洪钺，汪叔华.卡尔曼滤波与组合导航原理[M].西安:西北工业大学出版社,1998.

[15] 严恭敏，秦永元.车载激光捷联惯导系统双位置对准研究[J].弹箭与制导学报，2005,25(3)：478- 480.

[16] CHANG Guobin.Fast Two- position Initial Alignment for SINS Using Velocity Plus Angular Rate Measurements[J].Advances in Space Research,2015.56(7):1331- 1342.

[17] XIONG Jin,YANG Z H,GUO Huiqin.A Two- position SINS Initial Alignment Method Based on Gyro Information[J].Advances in Space Research,2014，53(11):1657- 1663.

[18] YU Fei,BEN Yueyang,LI Qian,et al.Optimal Two- Position Alignment for Strapdown Inertial Navigation System[J].International Conference on Intelligent Computation Technology and Automation,2008,2(2):158- 164.

[19] 毛玉良，陈家斌，宋春雷，等.捷联惯导姿态误差模型分析[J].中国惯性技术学报，2013,21(2)：182- 185.

[20] CHANG Lubin,HE Hongyang,QIN Fangjun.In- motion Initial Alignment for Odometer Aided Strapdown Inertial Navigation System Based on Attitude Estimation[J].IEEE Sensors Journal,2017,17(3):766- 773.

Two- position Alignment Method for Inertial Navigation System of Rail Tester

ZHANG Xinchun,CUI Ximin

(College of Geoscience and Surveying Engineering, China University of Mining and Technology, Beijing 100083, China)

In order to improve the alignment accuracy of inertial navigation system in rail tester, a two position alignment method for the inertial navigation system is proposed, which is using of u- turn mode, to achieve inertial navigation system accelerometer constant bias compensation. Select 0.1°/h FOG and 200 μg flexible quartz accelerometers making up inertial navigation system, and carry out a test. The results showed that the two position alignment method can effectively remove the orbital parameters detection error causing by inertial devices bias error. Continuous operation for 300 m, the railroad level detection accuracy is significantly improved.

inertial navigation system； rail tester； two position alignment

2016- 11- 09；

2017- 01- 17

国家自然科学基金面上项目(51474217) 作者简介： 张新春(1976—)，男，博士生，研究方向为惯性组合导航与轨道检测。E- mail：22501139@qq.com

张新春，崔希民.基于惯性导航系统的轨道检查仪双位置对准方法[J].测绘通报，2017(3)：5- 8.

10.13474/j.cnki.11- 2246.2017.0072.

P228

A

0494- 0911(2017)03- 0005- 04