单波束测深数据的插值精度分析

陈长波，刘小丁，朱紫阳，周 昆

(广东省国土资源测绘院，广东 广州 510500)

单波束测深数据的插值精度分析

陈长波，刘小丁，朱紫阳，周 昆

(广东省国土资源测绘院，广东 广州 510500)

基于误差传播定律，对稀疏的离散水深点内插值进行了精度分析，建立了单波束水深内插值中误差表达的数学模型，利用我国南方某海岸带的3个试验区的进行了试验。试验结果表明，反距离加权法、Shepard法和线性插值三角网法，辅以自适应搜索半径法，内插水深值粗差比例普遍低于5%，质量与效率上为较优的插值模型；内插值精度与数据源精度有关，但与数据源密度关系不大；在给定深度测量极限误差情况下，建议在制定有关数字水深模型标准时，对水深在20 m以内的格网点水深值极限误差可设置为0.4 m。

单波束；数字水深模型；内插；精度

数字水深模型(digital depth model，DDM)是海底地形地貌形态表达的基本内容和基础框架[1]，以数字形式逼真地模拟再现海洋环境，使人们可以更加直观地了解和探索海底地形地貌。数字水深模型的质量高低，直接影响海洋空间信息表达的准确性和舰船航行的安全性。近年来，随着多波束全覆盖水深测量技术的广泛应用，研究以海量多波束数据为基础，通过内插值构建高精度的数字水深模型，已有大量的研究成果，成果主要集中在插值精度、插值方法、不确定度、数据质量评估及计算效率等方面[1- 8]。然而，实际生产中还有大量测深数据是采用单波束进行测量的，特别是近海岸及江河湖泊等，而利用稀疏的离散水深点内插格网数字水深模型的方法研究尚比较少；针对稀疏的离散重力点、高程异常点内插格网重力异常或高程异常模型的方法，则有大量的研究[9- 10]。根据现行的相关测绘标准，可以采用格网点的高程精度来衡量陆地地表地貌的数字高程模型的精度[11]；同理，也可以采用格网点的水深精度来衡量数字水深模型的精度，此时，格网点的水深精度仅由离散点水深测量精度与内插精度两部分组成。本文将在此基础上，分析单波束测深内插精度，探讨如何界定水深模型的水深精度要求，为基于单波束测深成果构建高精度数字水深模型奠定基础。

1 水深插值及有关精度分析

根据现行规范要求[12]，单波束测深线由主测深线和检查线组成，格网化精度取决于主测深线上离散水深点的水深测量精度和内插精度，而内插精度受内插方法与离散点间距等多种因素影响，测量时设置的检查线可以为评估格网化插值精度提供条件和方法。顾及水深点的随机性，格网点处的插值精度和任意离散点处的插值精度具有同一性，故可直接利用检查线上的检查点内插值与测深值来评价内插精度及格网点的水深精度。任意检查点P的内插值zI与实测值zR差值

v=zI-zR

(1)

式中，内插值zI可由检查点P处临近的主测深线水深值内插得到。

由于主测深线内插值zI与检查线实测值zR不相关，故有

(2)

式中，mv为内插值与实测值差值中误差；mI为内插值中误差，即可用于评价数字水深模型格网点水深值精度；mR为水深测量中误差。mv和mR可由整个测区按照同类型观测数据计算得到，即

(3)

(4)

式中，N为整个测区具有有效内插值及实测值的检查点总数；Δ为整个测区主测深线与检查线交叉处重合点(按照规范要求两点相距图上1.0 mm以内[12])水深值的差值；n为整个测区重合点数，通常N≫n。则内插值中误差

(5)

根据式(5)求得的内插值中误差即可用于评价格网点水深值精度。

内插值的模型化表示

(6)

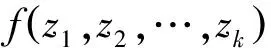
(7)

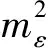
当给定测深值中误差限差mR限，由式(7)可得

(8)

常用插值方法主要有反距离加权法、Kriging法、Shepard法、移动曲面法、线性插值三角网法、双线性曲面法、最邻近点法、最浅点法等[1]。由于海底地貌形态的千变万化，相对均匀变化的重力异常和高程异常，适合于重力异常或高程异常插值的插值方法不一定适合于水深插值；陆地地表的数字高程模型的内插，由于其插值是基于特征点和特征线进行的，插值方法的优劣与特征点线有关，而数字水深模型的插值则基于相对分布均匀的水深点进行，无法充分体现水下地形的特征，故适合于陆地地表的高程插值的方法也不一定适合于水深插值。根据现有的针对多波束数据水深插值研究结果，在同一水深源数据密度条件下，移动曲面法、双线性曲面法、反距离加权法对水深内插精度要略高于最邻近点法和Kriging法，最浅点法的内插精度明显低于其他方法[1]，双线性曲面法是移动曲面法的特殊情况。为此，本文主要采用反距离加权法、Shepard法、加权移动曲面法[9]、线性插值三角网法共4种内插方法的插值精度。插值区域大小对插值结果的影响也较大，特别是海底地貌形态变化异常时尤为突出，为此采用自适应方式确定搜素半径。对于常见的内插模型，如反距离加权法、Shepard法等权函数小于等于1，则

(9)

相对应有

(10)

将式(10)带入式(8)，得

(11)

通过测区检查线求得的内插值中误差mI、水深测量中误差mR，即可求得内插值中误差限值与水深测量中误差限值的对应关系，从而明确格网水深值极限误差要求。

2 试验与分析

2.1 试验区域基本情况

根据试验需要，选择了如图1所示的我国南方某海岸带的3处水下地形测量成果，试验区域水深整体均呈非均匀变化，数据源的基本情况见表1。

分别利用主、检测深线上重合点按照式(4)计算了水深测量中误差，结果见表2。

2.2 试验结果及分析

本文采用反距离加权法、Shepard法、加权移动曲面法[9]、线性插值三角网法共4种内插方法的插值精度。插值区域大小对插值结果的影响也较大，特别是海底地貌形态变化异常时尤为突出，为此采用自适应方式确定搜素半径，得到各检查点的内插水深值，并与实测值进行比较，按式(3)计算内插值与实测值较差中误差，并按式(5)计算内插值中误差，在此基础上根据规范对深度测量极限的误差要求，按式(11)计算了内插值基线误差(置信度95%)，结果见表3。

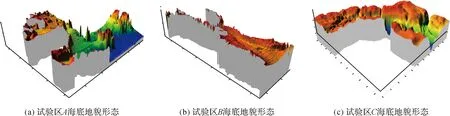
图1 各试验区展示

试验区测量时间比例尺定位系统测深系统面积/km2平均点密度(点/km2)试验区A2009年1∶10000信标差分GPSHD310单波束测深系统300119试验区B2010年1∶10000信标差分GPSHD310单波束测深系统380108试验区C2015年1∶2000信标差分GPSHD310单波束测深系统102749

表2 各试验区水深测量精度统计

注：试验区水深值绝大部分位于20 m以内，根据现行规范要求[12]，剔除较差大于0.5 m的粗差后再进行统计。

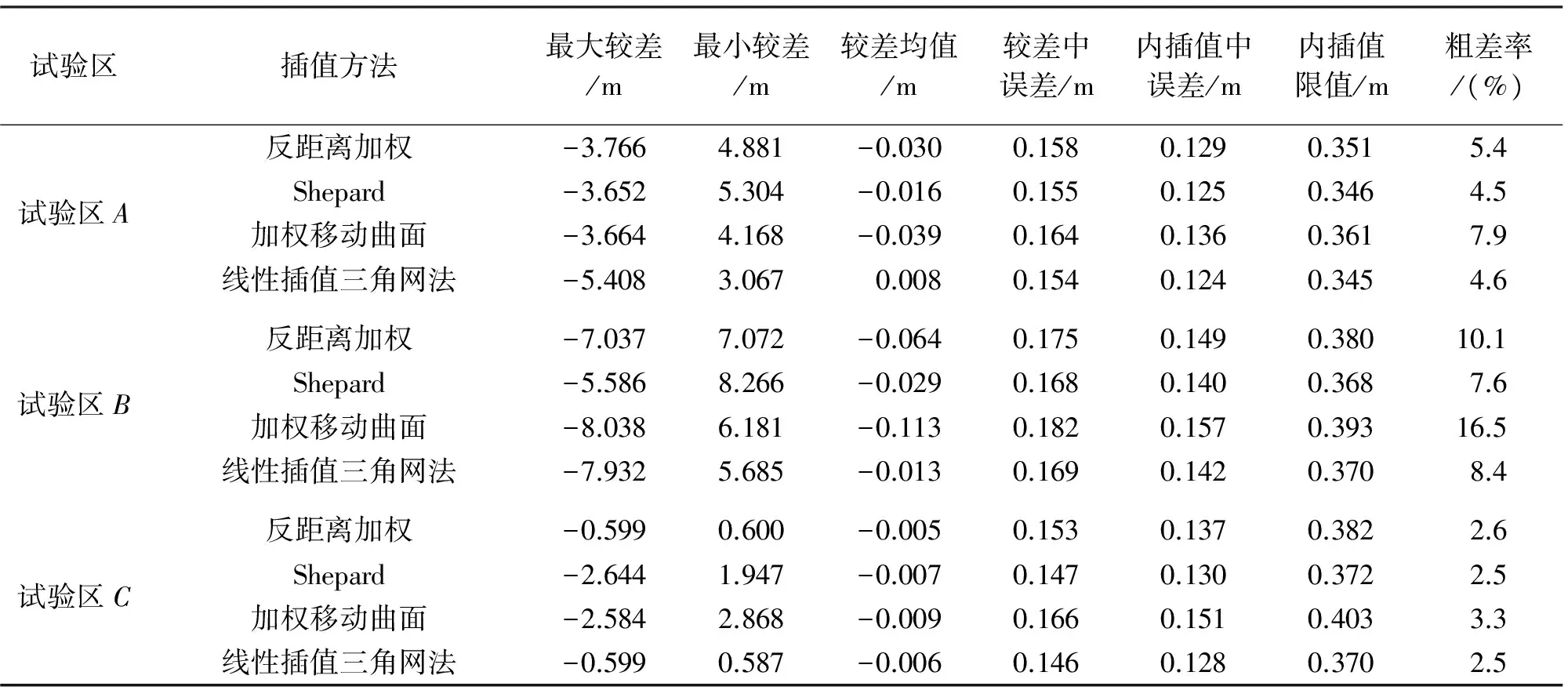
表3 各区域插值精度统计

注：根据现行规范要求[12]，主检重合点粗差限值0.5 m，并顾及插值的影响，在此设立粗差限值为0.6 m。

从表3可以看出，在同一水深源数据密度的条件下，反距离加权法、Shepard法、加权移动曲面法及线性插值三角网法的内插精度基本相当，但加权移动曲面法相对其他插值方法粗差比例略高。究其原因，主要是加权移动曲面法需要解算的参数相对较多，需要利用周边区域的水深点数多，虽然通过加权计算，但当海底地貌异常变化时，内插值与实际值差异还是较大，且该方法由于需要求解曲面参数，计算工作量相对其他插值方法也大。因此，对单波束水深数据的内插方法，综合考虑内插精度和计算效率，建议采用反距离加权法、Shepard法或线性插值三角网法。

从表3同时可以看出，内插值精度与数据源深度测量精度有关，试验区域C的深度测量高于其他试验区，内插值精度整体略高于其他区域，但差异不明显；数据源密度对内插值精度影响较小，试验区C数据源密度高于其他试验区，但内插值精度并未有明显提高。

在给定的深度测量极限误差(置信度95%)情况下，各试验区根据式(11)得到的内插值极限误差位于0.345～0.403 m的区间，整体差异不显著，结合深度测量极限误差要求，建议对水深在20 m以内的数字水深模型格网点水深值极限误差值可设置为0.4 m。

3 结 论

针对离散的单波束测深数据构建数字水深模型，推导了水深插值中误差及内插值限值计算公式，并采用具体实例进行试验及分析，得出如下结论：

(1) 常见的几种内插方法，内插水深值精度相当，但对于海底地貌形态复杂的区域，加权移动曲面法比其他方法粗差比例高、总体计算工作量大，在进行水深值内插中，建议采用反距离加权法、Shepard法或线性插值三角网法。

(2) 试验结果表明，内插值精度与数据源深度测量精度有关，与数据源密度关系不大，由于本文采用的试验区域水深在20 m以内，数据源深度测量精度差异不大，精度影响有限。

(3) 在给定的深度测量极限误差情况下，得到的内插值极限误差位于0.345～0.403 m的区间，整体差异不显著，结合水深测量的精度要求，建议对水深在20 m以内的数字水深模型格网点水深值极限误差设置为0.4 m。

[1] 贾帅东，张立华，彭认灿，等.基于多波束数据的网格水深模型内插方法精度分析[J]. 海洋测绘，2013，33(5)：24- 26，37.

[2] 董箭，彭认灿，郑义东，等. 局部动态最优Voronoi图的NNI算法及其在格网数字水深模型中的应用[J]. 测绘学报，2013，42(2)：284- 289，303.

[3] 董箭，彭认灿，郑义东. 利用局部动态最优Delaunay三角网改进逐点内插算法[J]. 武汉大学学报(信息科学版)，2013，38(5)：613- 617.

[4] 邹永刚，翟京生，刘雁春，等. 利用不确定度的海底数字高程模型构建[J]. 武汉大学学报(信息科学版)，2011，36(8)：964- 968.

[5] 贾俊涛，张哲，孟婵媛，等. 基于航渡式水深数据的海底地形DEM建模方法[J]. 海洋测绘，2014，34(5)：34- 36.

[6] 张立华，贾帅东，吴超，等. 顾及不确定度的数字水深模型内插方法[J]. 测绘学报, 2011, 40(3): 359- 365.

[7] 贾帅东，张立华，宋国大，等. 基于区域平均垂直不确定度的自适应格网水深建模方法[J]. 测绘学报, 2012, 41(3): 410- 416.

[8] 吴超，殷晓冬，张立华，等. 基于不确定度的多波束测深数据质量评估方法[J]. 海洋测绘，2009，29(5)：11- 14.

[9] 孙文，吴晓平，王庆宾，等. 高精度重力数据格网化方法比较[J]. 大地测量与地球动力学，2015，35(2)：342- 345.

[10] 张兴福,魏德宏. 基于似大地水准面格网的插值方法及精度分析[J]. 大地测量与地球动力学, 2011, 31(1): 113- 116.

[11] 基础地理信息数字成果 1∶5000 1∶10 000 1∶25 000 1∶50 000 1∶100 000数字高程模型：CH/T 9009.2—2010[S].北京：测绘出版社，2010.

[12] 海道测量规范：GB 12327—1998[S]. 北京：中国标准出版社出版，1999.

Accuracy Analysis for Single Beam Echosounder Interpolations

CHEN Changbo，LIU Xiaoding, ZHU Ziyang, ZHOU Kun

(Surveying and Mapping Institute， Land and Resources Department of Guangdong Province, Guangzhou 510500，China)

In the paper the accuracy for single beam echosounder interpolations using error propagation law is analyzed. A mathematical model of medium error expression for interpolation of water depth in single beam is established and the results in three experimental zones of a coastal zone in south China is tested. The inverse distance weighting method， shepard method and linear interpolation triangulation method with adaptive Search Radius Method are used to compute the gross error of water depth interpolations in this test. The results show that the ratio of gross errors is less than 5% and the three methods are superior in efficiency and quality. Also, we get that the interpolations’ accuracy is related to the precision of data source, but not to the density of data source. In the case of a given depth measurement limit error, we suggest that the limit value of Grid point water depth value should set to be 0.4m in the digital water depth model standards.

single beam echosounder; digital depth model；interpolation；accuracy

2016- 08- 08；

2017- 01- 13

2015年测绘地理信息行业标准项目；广东省国土资源科技专项(GDGTKJ2016001) 作者简介： 陈长波(1975—)，男，高级工程师，主要从事3S集成应用研究工作。E- mail：13500032401@139.com

陈长波，刘小丁，朱紫阳，等.单波束测深数据的插值精度分析[J].测绘通报，2017(3)：67- 70.

10.13474/j.cnki.11- 2246.2017.0086.

P229

A

0494- 0911(2017)03- 0067- 04