基于结构字典学习的图像复原方法

杨 航，吴笑天，王宇庆

(中国科学院 长春光学精密机械与物理研究所，吉林 长春 130033)

基于结构字典学习的图像复原方法

杨 航*，吴笑天，王宇庆

(中国科学院 长春光学精密机械与物理研究所，吉林 长春 130033)

本文提出一种新的结构字典学习方法,并利用它进行图像复原。首先给出结构字典学习的基本内容和方法，然后将傅里叶正则化方法和结构字典学习方法有效整合到图像复原算法中。结构字典学习方法是先将原图像进行结构分解，再分别学习出每个结构图像中的字典，最后利用这些字典对原图像进行稀疏的表示。结合傅里叶正则化，提出了一种有效的迭代图像复原算法：第一步在傅里叶域利用正则化反卷积方法得到图像的初步估计；第二步采用结构字典学习的方法对遗留的噪声进行去噪处理。实验结果表明，提出的方法在改进信噪比和视觉质量上都要优于6种先进的图像复原方法,改进的信噪比平均提升0.5 dB以上。

结构字典;字典学习;图像复原;反卷积

1 引 言

图像复原是一个经典的反问题，它广泛的存在于图像处理的各个领域中，包括：航空探测[1]、物理光学[2-3]、医疗诊断[4]以及天文观测等。举个例子来说，在捕获图像的过程中，相机可能会发生相对于拍摄目标的运动，因此在成像后就会导致运动模糊[5-6]，另外一个比较常见的例子就是离焦模糊.在数学上,图像模糊的过程可以表达为一个点扩散函数(point spread function,PSF)与真实图像之间的一个卷积，同时伴有噪声的干扰。一个降质观测图像y可以写成如下形式：

式中，uorig、y和h分别表示原始图像，观测图像和点扩散函数。γ表示在图像成像过程中引入的噪声，一般而言，都假设它为独立同分布的零均值高斯噪声，方差为σ2, “*”表示循环卷积。

在离散傅里叶变换(DFT)域中，方程(1)可以写成：

式中，Y、H、Uorig、Γ分别为y、h、uorig、γ的Fourier变换。模糊过程的逆过程被称作图像复原。图像复原的目的是从降质图像y重新构造真实的图像。而图像复原问题是著名的病态问题，因此为了获得图像的合理估计，需要用到正则化等相关方法。

在图像成像过程中噪声是广泛存在的，因而在图像高频部分小的变化都会导致振铃效应。Wiener滤波[7-8]和限制最小二乘[7]方法能够在频域快速估计出真实图像，但复原出的图像往往质量不高；基于全变差(total variantion,TV)模型的图像复原方法是现今比较流行的方法之一，具有代表性的方法有快速全变差复原(fast TV deconvolution,FTVd)[9]、极大极小全变差(majorization-minimization based TV,TVMM)[10]等等。这些方法具有很好的边缘保持能力，取得了不错的复原效果。然而，对于大部分自然图像，全变差模型经常导致细小尺度信息的丢失，例如纹理等。迭代阈值收缩(iterative shrinkage threshold,IST)算法也是近些年来被广泛使用的方法，在文献[11]中，IST方法在数学理论上被阐明，随后快速IST算法(fast IST algorithm,FISTA)[12]和两步迭代阈值收缩方法(two-step IST,TwIST)[13]对经典的IST方法进行改进。这两种方式可以处理一般的图像反问题，例如图像反卷积、图像去噪以及超分辨率重构(其基本数学模型与反卷积有很大程度的相似性[14-15])等，但相关的算法只是针对小波、全变差模型进行处理，所以也不能很好的解决细节丢失问题。现阶段，很多有效的图像复原方法采用了两步法[16-18]：第一步，对模糊图像进行直接逆滤波，比如Fourier逆滤波；第二步对第一步得到的图像使用去噪方法去除遗漏的噪声和振铃。因此各种有效的去噪方法都被用来进行图像复原，例如高斯混合模型(Gaussian mixed method,GMM)[19]、形状自适应离散余弦变换(shape adaptive-DCT,SA-DCT)[20]、以及块匹配的3D滤波(block matching 3D,BM3D)[21-22]。最近基于边缘保持滤波器的图像复原算法也取得了很好的处理效果[23,24]。另外，很多学者对字典学习的方法进行了广泛的讨论，例如K均值奇异值分解(K-means SVD,KSVD)[25]，模糊与清晰字典学习(blurred and shaped dictionary learning,BSDL)[26]等在图像复原问题上都取得了一定的效果，但这些方法大都没有很好的抑制振铃或者保持图像的细节清晰。单一的字典分解图像往往很难精确刻画图像的特征，因此学者们提出了双字典的方法用以描述图像[27-28]，主要利用图像中的不同特征，例如边缘、纹理等构造新的字典。更多有用的算法和技术可以参考文献[29-32]。

在本文中，我们首先提出结构字典学习的概念，然后利用结构字典学习提出一个有效的迭代复原算法。复原算法将Fourier正则化和字典学习技术有效的整合到同一个框架下。由于自然图像可以看成是由多个不同类型的结构图像组合而成的，因此对于各个结构图像采用不同的字典进行表示往往会得到优于整体字典表示的效果。由此，在本文中，我们给出了结构字典学习的概念，它能够对图像进行更加稀疏的表示。另外，提出的复原算法由两部分构成：逆滤波和去噪。在逆滤波过程中，虽然得到了信息丰富的估计图像，但却放大了噪声，同时引入了振铃；因此在去噪阶段，采用基于结构字典学习的方法能够有效的抑制噪声和振铃。最后,在实验部分, 通过与6种先进的图像复原算法的对比，验证了本文提出的算法有效性。

2 结构字典学习

本文提出了一种结构字典的学习方法，该方法利用图像中不同的结构信息来构造不同的字典，以此达到对图像更加稀疏的表示。例如，图像可以看成是由纹理和卡通两种结构组成，因此我们分别构造纹理字典和卡通字典，这样就能够对每个结构都有满足各自特点的字典(也可称为基底)，能够得到比一般字典学习方法更加优越的结果。

2.1 基于学习的稀疏表示

本小节简单回顾一下字典学习方法：基于图像块的稀疏分解。对于一个字典矩阵D=[d1,…,dK] ∈RL×K，一个信号x∈RL可以由 [d1,…,dK]的线性组合进行表示。在一般的图像处理应用中，L的值比较小，例如对于8×8大小的图像子块，L=64。当K=L时，D是一个满秩的矩阵，称D为完备的，当K>L时，字典D称之为过完备的。称字典D是适合信号x的，如果存在一个稀疏的向量α∈RK，使得x可以写成D与α的乘积，即x=Dα。

对于固定字典，如小波、曲波、轮廓波、剪切波、波原子等，它们往往将图像限制到某一种类型，而学习得到的字典是从当前图像中得到的，其应用范围可以适合于任何类型的图像。基于学习的字典包括自适应字典学习(K-SVD)[25]，局部字典学习[33]以及学习的稀疏编码[34]。这些稀疏表示的方法可以有效的对图像进行表示，非常有利于图像的去噪[25]、修补以及复原[35]，因为他们学习得到的字典比那些固定字典更加适合图像的各种先验估计。

s.t.‖

式中，S表示需要的稀疏度，而符号‖αt‖0表示向量的“l0范数”，意思是向量中非零元素的个数。特别是，Elad提出的K-SVD方法能够很好的从噪声图像b中恢复真实图像u：

‖Dαt-

式中，b=u+γ,E=[α1,α2,…,αT]表示图像子块的稀疏矩阵，λ>0 表示正则化参数。求解一般分为两个步骤交替进行：稀疏编码阶段(固定字典D求u和E)和字典D更新阶段(固定u和E求字典D)。

2.2 结构字典学习

针对自然图像，Elad等人提出了一种形态成分分析(morphological component analysis,MCA)的理论[36]，它是结合了图像的稀疏表示理论和变分优化方法，将图像分解成例如卡通成分和纹理成分等多种结构，再寻找能够对各个结构进行稀疏表示的字典(这里的字典是固定字典)，并把这种理论成功的应用在图像去噪和修补等问题中。受此工作的启发，我们将图像模型表示为光滑部分和纹理部分，即

式中，u1和u2分别表示图像的光滑部分和纹理部分，这个模型能够较好的逼近自然图像。为了能够对图像进行稀疏表示，需要对不同结构的图像分别建立相应的字典，各个字典能够较优的匹配图像中特定的局部结构。这些字典互相补充，组成一个结构字典集合。这个结构字典能够有效的匹配图像中的重要结构，形成对图像的有效表示。

对于图像的结构字典，我们给出一般形式：

本文采用一种简化的策略，第一步对图像b进行结构分解，第二步分别对每个结构图像进行字典学习，进行KSVD计算，这样就大大的节省了运算时间，同时还能保证处理效果。

对自然图像进行结构分离，研究人员提出了很多种办法。本文提出的算法采用卷帘导引滤波(Rolling guidance filter,RGF)[37]对图像进行结构/纹理分解。卷帘导引滤波是一种新的边缘保持滤波器，在光滑图像的过程中保持边缘不模糊，同时能够将图像中的纹理信息滤除.而这种性质非常适合于图像结构分解。记图像b的卷帘导引滤波为RGF(b)，则有：

z2=b-z1.

图1显示了卷帘导引滤波的结构纹理分离效果。

图1 卷帘导引滤波结构分解效果图Fig.1 Results of rolling guidance filter

其中，为了试验模糊和噪声对于图像分解的影响, 我们在图1的(d)～(f)给出了一个退化图像分解实例，从图中可以看出，RGF依然得到了一个较好的结构分解(图1中的(e)和(f))。

在得到当前图像的结构、纹理分解后, 分别对分解后的两幅图像进行单独的字典学习, 因此问题(6)可以用如下方式替换：

求解(9)和(10)的方法有很多，在本文中我们采用K-SVD[25]求解的原理，它是一种交替更新字典和稀疏矩阵的方法。K-SVD的核心是一种正交匹配追踪(Orthogonal Matching Pursuit,OMP)方法：第一步，选择与当前残差相关性最大的字典原子；第二步利用奇异值分解(SVD)顺序更新，每迭代一次更新一列，反复迭代，直到满足条件。OMP算法通过对字典原子进行正交处理，能够保证达到当前的最优解，即不存在反复迭代的情况，因此在相同条件下OMP算法的收敛速度很快。

通过对两个子问题的分别求解，最后我们得到了一组结构字典{D1,D2} 和一组结构图像{u1,u2}。 具体的求解步骤如下：

算法1 结构字典学习框架

输入：结构图像u1=z1和纹理图像u2=z2以及D1=D2=ODCT

输 出 ：重构图像u和结构字典D1,D2

循环：

Step1.稀疏编码阶段：使用OMP方法对每一个Rt(ui) 计算系数αi(i=1,2)，逼近如下问题的解：

Step2.字典更新阶段：对于字典Di(i=1,2)中的每一列(t=1,2,…,T)，使用奇异值分解(SVD) 顺序的更新它们，每次更新一列。

Step3.设学习得到的字典为D1,D2

u=u1+u2.

式中，ODCT表示过完备离散余弦变换，σ2为b(z1+z2)的方差。因为参数λi与当前图像中的方差有关，同时由于在对b卷帘导引滤波之后，在光滑部分的噪声方差会有所降低，因此z1和z2的方差是不同的,因此对各自参数的设置也是不同的,本文设C1=1.2,C2=1.8以及λ1=50/σ,λ2=25/σ。

3 基于结构字典学习的图像复原

本节将详细描述一种基于结构字典学习的图像复原方法。本文采用迭代的方式复原模糊图像.方法主要由两大部分构成：(1)傅里叶域上的正则化反卷积；(2)利用结构字典学习进行图像去噪。本节详细描述这两个部分。

与方程(4)类似，采用如下正则化模型：

‖Dαt-

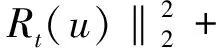
在这个模型中，卷积算子h和稀疏表示字典Dα是耦合的，因此我们采用一种分离变量的方法去除耦合，通过引入一个中间变量v将问题(11)转化为

令r=λ/ξ，则将上述问题分解成两个子问题：

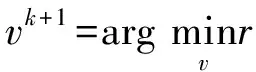
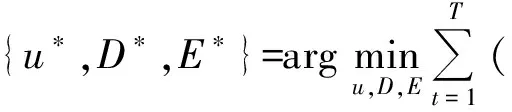
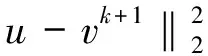
3.1 直接反卷积

图像复原的目标是将模糊的图像变清晰，对于局部信息的观测具有正效应，而它的负效应则是引入了振铃以及噪声。

考虑到方程(15)是一个简单的最小二乘问题，因此可以求出v的解析解。利用卷积定理，在Fourier域上，可以直接写出方程(13)的解：

式中，F表示DFT算子，F*表示其复共轭.算式中的加、减、乘、除均为逐像素运算。

正则化参数rk在本方法中起着重要作用，需要在每一次迭代中进行更新。在实践中，我们发现大的rk能够较为明显的降低噪声的方差，但却会导致较为明显的振铃效应。因此应该选择较小的rk，这样虽然遗留了更多的噪声，但是能够保留图像中更多的边缘、纹理等信息，这样在接下来的去噪阶段，有效的结构字典学习方式能够去除遗留噪声同时保留更多的图像细节信息。

对于一个N×N大小的图像，在第k步迭代，使用如下公式计算参数rk：

在直接逆滤波之后，对F(vk+1)做Fourier逆

变换，就得到了含有噪声以及丰富细节信息的图像。接下来将对这个结果图像vk+1进行去噪处理。

3.2 利用结构字典学习的振铃消除

图像的稀疏性质和字典学习在图像去除高斯白噪声上展现了很大的优势，因此我们将提出的结构字典学习整合到图像复原中，期望能够很好的去除直接反卷积后遗留的噪声。

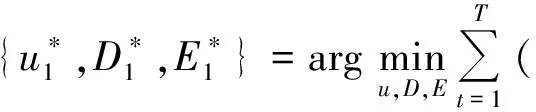
问题(21)和(22)恰是本文第二节中所描述的结构字典学习问题，因此我们采用“算法1”结构字典学习框架来处理，即可得到最优解。

特别的是，由于在复原过程中，图像的噪声方差会随着参数的不同而改变，因此我们使用文献[38]中的方法来估计。

最后我们总结提出的图像复原算法：

算法2 基于结构字典学习的图像复原算法

输入：u0=0,D1=D2=ODCT

输出：uiter

迭代k=1,2…,iter

Step1 傅里叶正则化：利用式(18)获得vk+1；

传统的字典学习方法没有考虑到图像内容的差异性，只学习得到一组字典，在图像处理中缺乏对图像各种结构的区分性，不能够根据图像不同结构的性质来适时选择合适的方法，这样就可能对图像的复原效果产生偏差；另外，在图像复原的过程中，虽然基于稀疏表示的单字典学习方法已经能够重构出高质量的复原图像，但是还是无法避免丢失一部分细节信息，这就大大地影响了复原图像的视觉质量。

本文提出的基于结构字典学习的图像复原方法，较好地整合了字典学习的方法与结构分解的方法，从而构建了用于进行图像复原的双字典。根据图像内容的差异，将图像分成结构部分和纹理部分，分别构建适合自身性质的字典，使得学习得到的字典集合的适应性更强，对图像的稀疏表达更有效。

4 数值实验

本文的实验采用的参数如下：图像子块大小为8×8个像素，字典选择为L=64,K=256。为了验证提出的算法的有效性，考虑7组经典复原实验，这些实验被广泛用在图像复原算法的验证实验中,例如文献[19][26]等。在这些实验中，原始图像分别为256×256大小的“House”图像(实验1,2)，512×512大小的“Lena”图像(实验3,4)和512×512大小的“Barbara”图像(实验5,6,7).使用3种点扩散函数(pointspreadfunction,PSF)：

PSF1：hi,j=1/81, i,j=-4,…,4

PSF2：[1,4,6,4,1]T[1,4,6,4,1]/256

PSF3：25×25，方差为1.6的高斯核函数

所有的点扩散函数都进行了归一化∑hi,j=1。具体的实验设置如下：

·Experiment1:PSF1, σ2=0.165,andHouse

·Experiment2:PSF3, σ2=4,andHouse

·Experiment3:PSF1, σ2=0.195,andLena

·Experiment4:PSF3, σ2=4,andLena

·Experiment5:PSF2, σ2=49,andBarbara

·Experiment6:PSF3, σ2=4,andBarbara

·Experiment7:PSF1, σ2=0.49,andBarbara

表1给出本文的算法与现今主流算法的数值对比。在本小节中，通过上述7组实验与ForWaRD(Fourierandwaveletregularizationdeconvolution)[16]，FTVd[9]，BM3DDEB(blockmatching3Dfilteringbaseddeblurring)[22]，L0-ABS(L0normanalysisbasedsparseoptimization)[30]，BSDL[26]以及SURE-LET(Stein′sunbiasedriskestimate-linearexpansionofthresholds)[32]等6种算法进行对比，其实验数据均由中其作者提供的程序以及建议的参数设置而得到。

表1 本文算法与现今主流算法ISNR值对比

在这些实验中，我们使用改进的信噪比(improvement signal to noise rate,ISNR)来衡量算法的有效性。ISNR的定义如下：

在实验Exp1和Exp2中，“House”图像被两种不同的模糊核降质，且被高斯白噪声干扰。在表1中的第2和第3栏给出不同算法获得的ISNR值。从ISNR值中可以看出，本文的方法要好于其他几种图像复原方法，图2显示针对Exp2各个算法复原出的图像细节。从图2(c)中可以看，ForWaRD算法的结果对比度较低同时还有一些振铃存在(房子的顶部)；FTVd的处理效果(图2(d))在图像中存在一些块效应，例如窗户附近； SURE-LET的算法得到的效果显示在图2(e)中，仔细观察可以看出在窗户附近依然有些振铃；图2(f)是BSDL的处理效果，在白色竖直边缘依然比较模糊;而BM3DDED的复原效果有明显的振铃，见图2(g)。本文方法得到的效果显示在图2(h)中，可以看出图像的一些边缘得到了恢复，如窗户，房顶等。

图2 Exp2视觉效果对比图Fig.2 Visual comparison of House image in Exp2

实验Exp3和Exp4是对模糊的“Lena”图像进行复原.数值模拟结果显示在表2的Exp3和Exp4栏中。从ISNR值可以看出，本文的方法要好于其他6种算法。图3显示的是Exp3各个算法的复原图像细节。从图3的对比中可以发现，本文提出的方法不仅在ISNR上有着一定的优势，而且在视觉效果上也要好于其他几个算法。

在实验Exp5、Exp6和Exp7中，实验图片是纹理信息丰富的“Barbara”。分别用PSF2、PSF3和PSF1来模糊原始清晰图像，同时加入一定量的噪声。不同算法的ISNR结果总结在表1的最后3栏中。同样可以发现，在对比的算法中，我们的方法依然取得了较好的结果.在图4中给出了Exp5的复原图像细节对比。从图4(c)中可以看出，ForWaRD算法复原的效果几乎将原来裤子中的纹理全部丢失，而图4(d)显示的是FTVd的效果，依然有噪声残留下来。图4(e)和4(f)分别显示的是L0-ABS和BSDL的效果，可以看到Barbara的裤线中大部分的细节已经不见了。BM3DDEB的处理效果显示在图4(g)中，可以看到在裤子的周围，有振铃残留；图4(h)显示的是本文的算法得到的效果，从视觉效果上看，它要好于图4(c)～4(g)。

图3 Exp3视觉效果对比图Fig.3 Details of the image deconvolution experiment with a Lena in Exp3

图4 Exp5视觉效果对比图Fig.4 Details of the image deconvolution experiment with a Barbara in Exp5

图5给出了Exp7中本文方法与BSDL算法的效果对比。从图中可以明显看出，同为字典学习类的图像复原方法，我们的方法在视觉质量和ISNR数值上都要好于BSDL方法。主要原因在于我们使用了分别表示纹理和结构的双字典，相对于仅仅使用单一字典的学习方法，更有利于对图像进行稀疏表示。

图5 Exp7实验效果对比图Fig.5 Details of the image deconvolution experiment with a Barbara in Exp7

在表2中，我们给出了各个算法的运算时间。因为各个方法的运算时间都只与图像分辨率有关，因此我们给出不同分辨率下各个算法的时间对比。

表2 本文算法与现今主流算法实验运行时间(秒)对比

5 结 论

在本文中，我们提出结构字典学习方法和利用结构字典学习的图像复原算法.首先根据自然图像的一般特性，将图像分为平滑部分和纹理部分，然后分别对两部分构造字典，进而得到对各个部分的稀疏表示。最后采用一种分离变量的思想对正则化复原模型中的卷积算子和字典表示进行解耦和，得到了一个迭代格式。同时数值模拟实验，本文提出的复原算法要好于现今6种经典复原算法， ISNR值平均提升0.5 dB以上。将来的主要工作是想将该方法引申到盲复原方法中，将点扩散函数(模糊核)的估计与字典学习整合到一起.同时该方法也可以延伸到其他图像问题中，例如图像去噪和超分辨率重构等。

[1] 沈峘, 李舜酩,毛建国,等.数字图像复原技术综述[J].中国图像图形学报，2009，14(9):1764-1775. SHEN H,LI S M,MAO J G,etal.. Digital image restoration techniques:a review[J].J.ImageandGraphics,2009，14(9):1764-1775.(in Chinese)

[2] 杨亚威,胡双演,张士杰,等.基于字典对联合学习的退化图像复原方法[J].计算机辅助设计与图形学学报,2015,3:406-413. YANG Y W,HU SH Y，ZHANG SH J,etal.. A degraded image restoration approach based on pairs of dictionaries jointly learning[J].J.Computer-AidedDesign&ComputerGraics,2015,3:406-413.(in Chinese)

[3] 陈曦,汪彦刚,彭思龙,等.部分模糊核已知的混合模糊图像复原算法[J].计算机辅助设计与图形学学报,2010,2:272-278. CHEN X,WANG Y G,PENG S L,etal.. Restoration of degraded image from partially known mixed blur[J].J.Computer-AidedDesign&ComputerGraphics,2010,2:272-2781.(in Chinese)

[4] JAIN A K.FundamentalofDigitalImageProcessing[M]. Prentice-Hall. Inc.,1989:1420-1424.

[5] 朱明,杨航,贺柏根,等.联合梯度预测与导引滤波的图像运动模糊复原[J].中国光学,2013,6(6):850-855. ZHU M,YANG H,HE B G,etal.. Image motion blurring restoration of joint gradient prediction and guided filter[J].ChineseOptics,2013,6(6):850-855.(in Chinese)

[6] 刘成云,常发亮.基于稀疏表示和Weber定律的运动图像盲复原[J].光学 精密工程,2015,23(2):600-608. LIU C Y,CHANG F L. Blind moving image restoration based on sparse representation and Weber′s law[J].Opt.PrecisionEng.,2015,23(2):600-608.(in Chinese)

[7] BANHAM M R,KATSAGGELOS A K. Digital image restoration[J].IEEESiggcalProcessingMagazine,1997,14(2):24-41.

[8] HANSEN P C.Rank-deficientandDiscreteill-posedProblems:NumericalAspectsofLinearInversion[M]. Philadelphia,PA:SIAM,1998.

[9] WANG Y,YANG J,YIN W,etal.. Anew alternating minimization algorithm for total variation image reconstruction[J].SIAMJ.Imag.Sci.,2008,1(3):248-272.

[10] OLIVEIRA J,BIOUCAS-DIAS J M,FIGUEIREDO M A,etal.. Adaptive total variation image deblurring:a majorization-minimization approach[J].SignalProcessing,2009,89(9):1683-1693.

[11] DAUBECHIES I,DEFRISE M,AND MOL C,etal.. An iterativethresholding algorithm for linear inverse problemswith a sparsity constraint[J].CommunicationsonPureandAppliedMathematics,2004,57(11):1413-1457.

[12] BECK A,TEBOULLE M A. Fast iterativeshrinkage-thresholding algorithm for linear inverseproblems[J].SIAMJ.Imag.Sci.,2009(2):183-202.

[13] BIOUCAS-DIAS J,FIGUEIREDO M. A new TwIST:two-step iterative shrinkage/thresholding algorithms for image restoration[J].IEEETrans.ImageProcess,2007,16(12):2992-3004.

[14] 张振东,陈健,王伟国,等.基于SSIM_NCCDFT的超分辨率复原评价方法研究[J].液晶与显示,2015,30(4):713-721. ZHANG ZH D,CHEN J,WANG W G,etal.. Evaluation method of super-resolution restoration based on SSIM_NCCDFT[J].ChineseJ.LiquidCrystalsandDisplays,2015,30(4):713-721.(in Chinese)

[15] 郭萌,赵岩,王世刚,等.基于区域选择的红外弱小目标超分辨率复原算法[J].液晶与显示,2016,31(4):415-420. GUO M,ZHAO Y,WANG SH G,etal.. Infrared dim-small target super-resolution restoration algorithm based on region selection[J].ChineseJ.LiquidCrystalsandDisplays,2016,31(4):415-420.(in Chinese)

[16] NEELAMANI R,CHOI H,BARANIUK R G. ForWaRD:Fourier-wavelet regularized deconvolution for ill-conditioned systems[J].IEEETrans.SignalProcess,2004,52(2):418-433.(in Chinese)

[17] PATEL V M,EASLEY G R,HEALY D M. Shearlet-based deconvolution[J].IEEETrans.ImageProcess,2009,18(12):2673-2685.

[18] YANG H,ZHANG Z B. Fusion of wave atom-based wiener shrinkage filter and joint non-local means filter for texture-preserving image deconvolution[J].OpticalEngineering,2012,51(6):67-75.

[19] GUERRERO-COLON J A,MANCERA L,PORTILL J. Image restoration using space-variant Gaussian scale mixtures in overcomplete pyramids[J].IEEETrans.ImageProcess,2007,17(1):27-41.

[20] FOI A,DABOV K,KATKOVNIK V,etal.. Shape-adaptive DCT for denoising and image reconstruction[J].SPIE,2006,6064:203-214.

[21] DABOV K,FOI A,KATKOVNIK V,etal.. Image denoising by sparse 3D transform-domain collaborative filtering[J].IEEETrans.ImageProcess,2007,16(8):2080-2095.

[22] DABOVE K,FOI A,Image restoration by sparse 3D transform-domain collaborative filtering[J].SPIE,2008,6812:681207-12.

[23] YANG H,ZHU M,ZHANG Z B,etal.. Guided filter based edge-preserving image non-blind deconvolution[C]. Proc. 20th IEEE International Conference on Image Processing(ICIP),Melbourne,Australia,2013:4593-4596.

[24] YANG H,ZHANG Z B,ZHU M,etal.. Edge-preserving image deconvolution with nonlocal domain transform″[J].OpticsandLaserTechnology,2013,54:128-136.

[25] ELAD M,AHARON M. Image denoising via sparse and redundant representations over learned dictionaries[J].IEEETransactionsonImageProcessing,2006,15(12):3736-3745.

[26] COUZINIE-DEVY F,MAIRAL J,BACH F,etal.. Dictionary learning for deblurring and digital zoom[EB/OL]. [2011-09-28]. https://hal.inria.fr/inria-00627402.

[27] JAIN A K,CAO K. Fingerprint image analysis:role of orientation patch and ridge structure dictionaries[J].GeometryDrivenStatistics,2015:121-288.

[28] LI K,SHAO F,JIANG G,etal.. Joint structure texture sparse coding for quality prediction of stereoscopic images[J].ElectronicsLetters,2015,51(24):1994-1995.

[29] YUAN L,SUN J,QUAN L,etal.. Progressive inter-scale and intra-scale non-blind image deconvolution[J].ACMTransactiononGraphics,2008,27(3):74-83.

[30] PORTILLA J. Image restoration through l0 analysis based sparse optimization in tight frames[C]. Proc. 16th IEEE ICIP,Cairo,Egypt,2009:3909-3912.

[31] NI J,TURAGA P,PATEL V M,CHELLAPPA R. Example-driven manifold priors for image deconvolution[J].IEEETrans.ImageProcess,2011,20(11):3086-3096.

[32] XUE F,LUISIER F,BLU T. Multi-wiener SURE-LET deconvolution[J].IEEETrans.ImageProcess,2013,22(5):1954-1968.

[33] CHATTERJEE P ,MILANFAR P . Clustering-based denoising with locally learned dictionaries[J].IEEETrans.ImageProcess,2009,18(7):1438-1451.

[34] MAIRAL J,BACH F,PONCE J,etal.. Non-local sparse models for image restoration[C]. Proc. IEEE Int. Conf. Comput. Vis.,Kyoto,Japan,2009:2272-2279.

[35] LIU Q G,WANG S S,YING L L,etal.. Adaptive dictionary learning in sparse gradient domain for image recovery[J].IEEETransactionsonImageProcessing,2013,22(12):4652-4663.

[36] STARCK J L,ELAD M,DONOHO D ,etal.. Redundant multiscale transforms and their application for morphological component analysis[J].J.AdvancesinImagingandElectronPhysics,2004,132:287-348.

[37] ZHANG Q,SHEN X Y,XU L,etal.. Rolling guidance filter[C]. Europ. Conf.Comput.Vision. Springer,2014:815-830.

[38] YANG H,ZHU M,WU X T,etal.. Dictionary learning approach for image deconvolution with variance estimation[J].AppliedOptics,2014 53(24):5677-5683.

Image restoration approach based on structure dictionary learning

YANG Hang*, WU Xiao-tian, WANG Yu-qing

(ChangchunInstituteofOptics,FineMechanicsandPhysics,ChineseAcademyofSciences,Changchun130033,China)

*Correspondingauthor,E-mail:yhang3109@163.com

In this paper, we propose a new structure dictionary learning method, and perform image restoration based on this approach. First, we define the structure dictionary for the nature image. Second, an iterative algorithm is proposed with the decouple of deblurring and denoising steps in the restoration process, which effectively integrates the Fourier regularization and structure dictionary learning technique into the deconvolution framework. Specifically, we propose an iterative algorithm. In the deblurring step, we involve a regularized inversion of the blur in Fourier domain. Then we remove the remained noise using the structure dictionary learning method in the denoising step. Experiment results show that this approach outperforms 6 state-of-the-art image deconvolution methods in terms of improvement signal to noise rate(ISNR) and visual quality, and the ISNR can be improved by more than 0.5 dB.

structure dictionary;dictionary learning;image restoration;deconvolution

杨 航(1985—)，男，吉林长春人，博士，助理研究员，20012年于吉林大学获得博士学位，主要从事机器视觉及图像复原方面的研究。E-mail:yhang3109@163.com

2016-10-12；

2016-12-05

国家自然科学基金资助项目(No.61401425) Supported by National Natural Science Foundation of China(No.61401425)

2095-1531(2017)02-0207-12

TP391

A

10.3788/CO.20171002.0207