变换光学透镜天线研究进展

曹尚文，周永江，程海峰

(国防科技大学 新型陶瓷纤维及其复合材料国防科技重点实验室，湖南 长沙 410073)

变换光学透镜天线研究进展

曹尚文，周永江*，程海峰

(国防科技大学 新型陶瓷纤维及其复合材料国防科技重点实验室，湖南 长沙 410073)

龙伯透镜天线是一种独特的渐变折射率透镜天线，但因为某些缺陷其应用受到限制。近年来，人们采用变换光学方法和超材料理论设计了许多以平板龙伯透镜为代表的新型透镜天线。本文对比总结了变换光学设计透镜的3种方法，即坐标变换法、保角变换法和准保角变换法；指出了准保角变换法由于设计灵活、可使用全介电材料制备而更具研究和应用前景；详细阐述了准保角变换法设计透镜的原理和步骤；介绍了国内外关于透镜变换和制备具有影响力的研究成果；指出了变换光学透镜天线今后的研究方向。

透镜天线；龙伯透镜；变换光学；超材料；准保角变换法

1 引 言

透镜天线是利用透镜的聚焦特性，将点源或线源发出的球面波或柱面波转换为平面波束的天线，通过合理设计透镜表面形状和折射率，调节电磁波的相速以获得辐射口径上的平面波前。依靠表面形状实现聚焦功能的透镜主要包括介质减速透镜和金属加速透镜，其制作材料是均一的，通过改变不同路径光束在透镜中行走的距离来改变光程。还有一类是渐变折射率透镜，其中最引人注目的当属龙伯透镜。

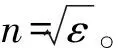
近年来，随着超材料(Metamaterial)的兴起和变换光学(Transformation Optics)理论的提出，许多新型透镜天线被设计出来，也有许多研究者将目光投向传统龙伯透镜的改进上，龙伯透镜有望重获新生。采用变换光学方法可以将龙伯球压缩成平板透镜，不仅体积轻巧，还可以具有平面的聚焦面，易于集成。变换后的龙伯透镜电磁参数发生改变，仍是一种渐变折射率结构，而使用超材料技术可以有效地实现对结构电磁参数的控制，降低加工难度和制作成本，这些都将使龙伯透镜在天线领域的竞争中更具优势。

采用变换光学方法设计透镜是研究新型透镜天线的第一步，也是关键步骤。事实上，变换光学理论最早是在电磁隐身领域提出并不断发展的[4-8]，后来逐渐应用于设计一些新型电磁器件例如电磁集中器[9]、移相器[10]、弯折波导等[11]，新型透镜天线就是其中之一。回顾其发展历史，2006年，Pendry和Leonhardt在同一期《Science》期刊上发表文章各自独立地提出了变换光学理论，其中Pendry采用的是坐标变换法[12]，Leonhardt采用的是保角变换法[13]。变换光学简单来说是一种实现“弯曲空间”和“非均匀介质”之间等价变换的方法[14-15]，即通过改变空间的电磁参数实现对电磁波传播路径的控制。其物理基础是麦克斯韦方程的形式不变性，核心思想是坐标变换，这涉及两个空间，实际空间和虚拟空间。要使电磁波在实际空间中的传播路线与虚拟空间中相同，可以通过坐标变换建立变换前后空间的联系，但其代价是变换后空间的电磁参数也发生了改变，这种改变由空间的坐标变换法则确定。这种复杂的电磁参数分布通常使用具有独特电磁响应的超材料来实现。

超材料又可称作“人工电磁材料”，是指具有自然界材料不具有的特殊电磁特性的人工复合结构，以等效介电常数和等效磁导率描述其电磁特性，其宏观性质不仅与组成媒质有关，还由组合方式决定[16-17]，使得人们可以人为调控材料的电磁参数。超材料包括负折射率材料[18]、光子晶体[19]和高阻抗表面[20]等其他人工电磁结构。使用超材料制备龙伯透镜取得了许多进展，例如使用金属谐振结构超材料制备二维龙伯透镜[21-22]，采用打孔法[23,24]和3D打印方法[25-26]制备介质材料龙伯透镜等。

采用变换光学方法设计新型透镜，研究人员进行了多种变换的尝试，这些设计方法主要可以分为三类：坐标变换法(coordinate transformation)、保角变换法(conformal mapping，或称共形变换法)和准保角变换法(quasi-conformal mapping，或称准共形变换法)。由于坐标变换方法简单直观，理论成熟，早期研究者大都使用坐标变换方法[27-35]，但是这种透镜却由于电磁参数复杂难以制备出来。保角变换法虽然不存在这个问题，但设计的灵活性很差，研究甚少。后来集二者优点于一身的准保角变换法逐渐受到了研究者的青睐。

2 坐标变换透镜

2.1 坐标变换原理

采用坐标变换方法设计透镜的基础是Pendry教授的坐标变换理论：

在笛卡尔坐标系中，假设某一点变换前的坐标为r=(x,y,z)，变换后坐标变为为r′=(u,v,w)。即坐标变换可以表示为：

原空间的无源麦克斯韦方程组为：

由于麦克斯韦方程组具有形式不变性，在变换后的空间仍然可以写为：

其中

上式中，Λ是雅克比矩阵，是描述空间坐标变换的转换矩阵，T代表矩阵转置，-1代表矩阵的逆。由此，我们就可以根据特定的坐标变换方法得到变换后空间的介电常数和磁导率的分布。

2.2 坐标变换透镜的理论设计

最早将坐标变换理论应用到透镜天线领域的是Fanmin Kong等人[27]，2007年，他们设计了一种平板聚焦天线，将传统的抛物面天线压缩成一个平板，如图1(a)所示。并且假设电场是沿z向极化的TE波，只需考虑材料的μxx、μyy和εzz这3个参数即可。

他们所采用的变换函数为：

变换的雅克比矩阵为：

这种变换方式虽然简单，但是得到的电磁参数张量含有非对角分量，非常复杂。在简化后，μxx、μyy和εzz分如图1(b)所示，μyy和εzz分别分布在0～1和0～1.5之间，而μxx在边界处的值却接近40。图1(c)和图1(d)分别是采用有限元方法仿真得到的透镜天线与原抛物线天线的电场图，可以看出二者性能差别不大，但是这种非均匀强各向异性的电磁参数分布几乎不可能实现。

图1 抛物面坐标变换透镜[27]Fig.1 Coordinate transformation of the parabolic lens[27]

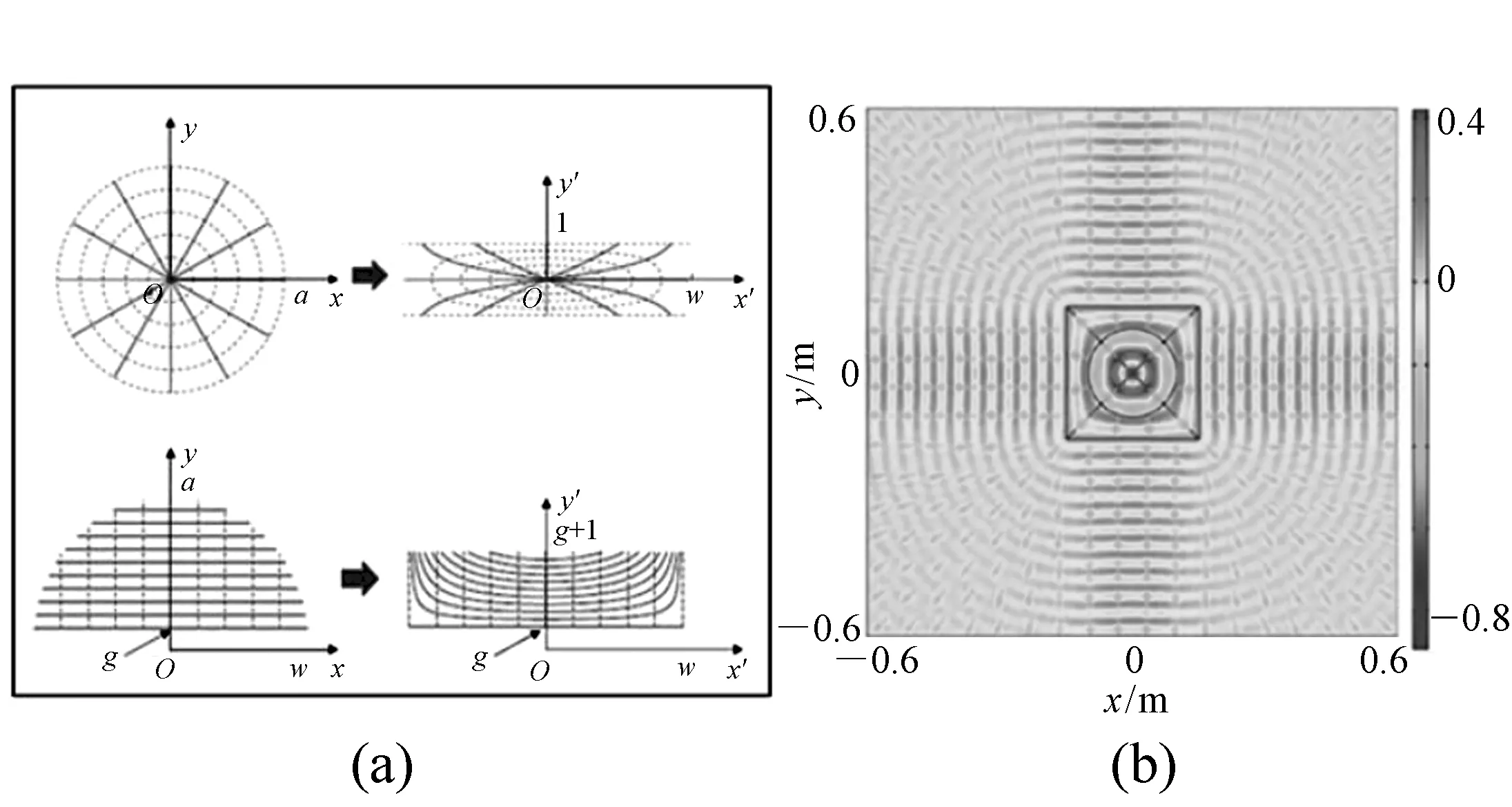
图2 DH.Kwon等[28]设计的两种变换(a)和蒋卫祥[29]提出的四向透镜天线(b)Fig.2 Two transformations(a) designed by DH.Kwon[28]and the four-beam antenna(b) proposed by Jiang Weixiang[29]

2008年，D.H.Kwon[28]将坐标变换方法应用在球形透镜上，在二维条件下分别对圆形区域和半圆形区域进行变换，设计出了一种波束准直透镜和一种平板透镜(如图2(a)所示)。

蒋卫祥[29]提出了一种四向透镜天线，采用拉伸变换将圆形区域变换为正方形区域，并采用有限元方法仿真了天线的近场电场分布(如图2(b)所示)。中心馈源发出的球面波经过透镜后，在四个方向上都变为了平面波，因此可以很好地用作高增益天线或波束准直器。

.

(9)

经过这种离散的坐标变换后，每一层的电磁参数张量都是均匀的且对角化的。而且，在TE波且电场沿z轴正向的条件下，只要保证μxxεzz、μyyεzz不变，电磁波在平面内的传播行为就不会改变。因此电磁参数又可以继续调整，μxx和εzz在整个区域内可以保持不变，只有分量μyy随着层数变化而改变，从而大大降低了实现难度。图3(b)是几种不同简化程度的透镜天线和常规介质透镜天线仿真结果对比图。

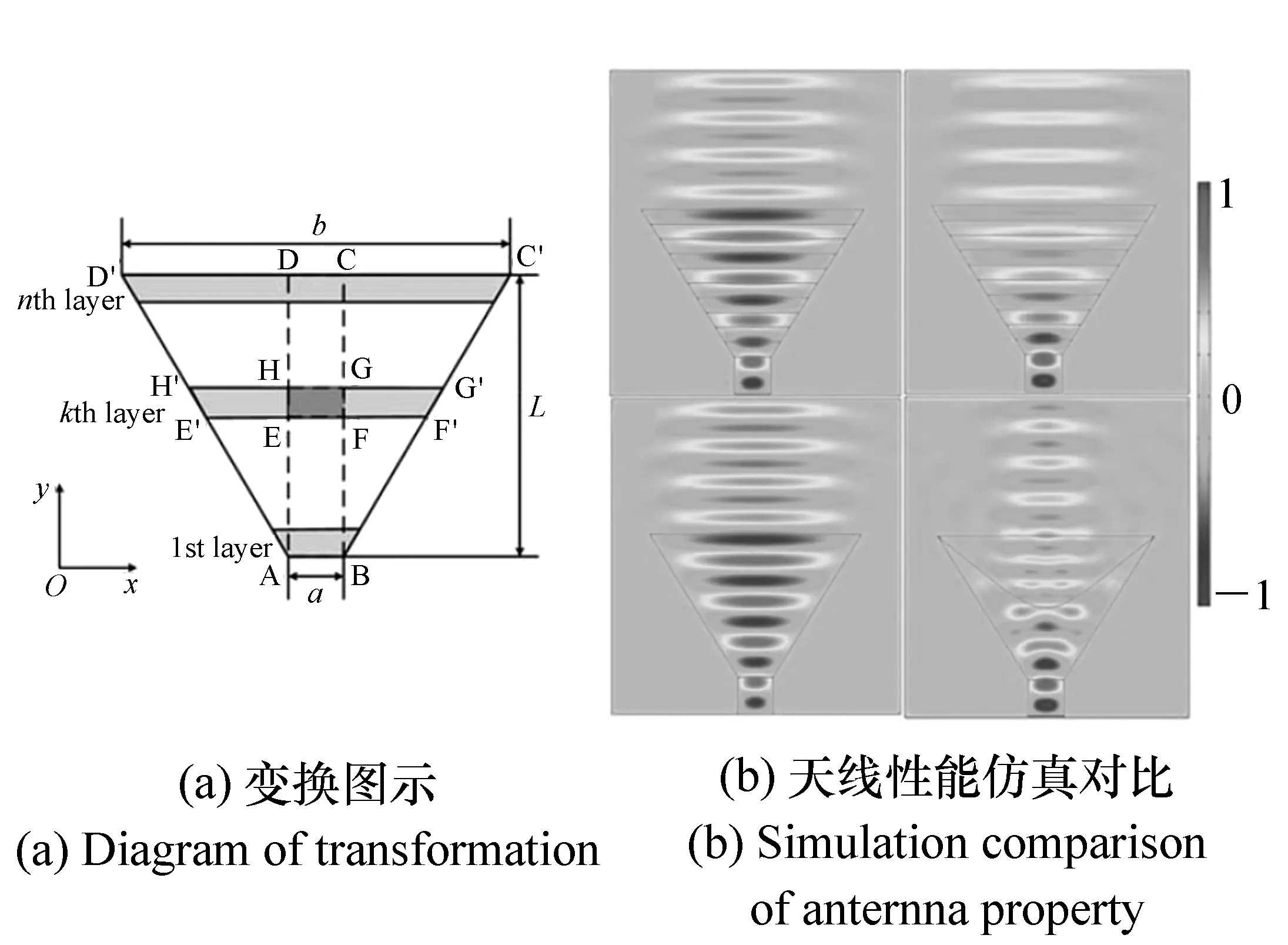
图3 分层坐标变换透镜[26]Fig.3 Layered coordinate transformation lens[26]

坐标变换方法得到的透镜具有很强的各向异性，介电常数和磁导率张量中含有非对角分量，这种强各向异性的电磁参数使用超材料也难以实现，有时得到的介电常数和磁导率分量还会趋近于0或呈现负值，虽然使用金属线和谐振环组成的超材料可以实现这种电磁参数，但是由于工作在谐振频率下，使得工作频带窄且损耗较大，即便人们想尽办法对电磁参数进行简化，实现透镜的制备仍然相当遥远。

3 保角变换透镜

相对于坐标变换法，保角变换法设计的透镜电磁参数是各向同性的，这对于透镜的实现非常有利。但由于变换函数对变换区域的限制严格，设计的灵活性差，因此基于此方法的研究例子甚少[36-38]。

保角映射是复变函数中的一类映射，利用保角映射可以解决许多物理问题包括热传导问题、电势问题和流体流动问题等。Leonhardt将它应用于变换光学之中。下面介绍保角映射的基本原理。对于一个复变函数w=g(z)=g(x+iy)=u(x,y)+iv(x,y)，可以看作是复平面z=x+iy到另一个复平面w=u+iv的映射。如果这个复变函数是解析的，那么这个映射就是保角映射，这会使得z平面上的两条曲线在变换到w平面后保持夹角不变。复变函数解析是指其满足柯西-黎曼条件，即：

.

.

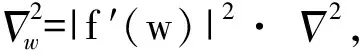
ψ=0 .

从而得到实际空间中折射率的表达式为：

.

可以看出，保角变换法得到的电磁参数不存在各向异性的问题。基于此方法，Kan Yao等人[37]设计了一种光学透镜，将一个圆形区域变换成了上半平面，采用的变换公式如下：

.

图4(a)表示馈源向外辐射的电磁波，在变换前后空间中传播的情况，实线代表电磁波的传播路径，虚线代表波阵面，可以看出波阵面由柱面变成了平面。图4(b)是得到的折射率分布。但是这种透镜功能有限，仍然是一种弧面的渐变折射率透镜，改进效果不明显。

过了夜，日本宪兵在门外轻轻敲门，走进来的，看样像个中国人，他的长靴染了湿淋的露水，从口袋取出手巾，摆出泰然的样子坐在炕沿慢慢擦他的靴子，访问就在这时开始：

图4 Kan Yao设计的光学透镜[37]Fig.4 Optical lens designed by KanYao[37]

4 准保角变换透镜

4.1 准保角变换原理

单独采用坐标变换法和保角变换法设计透镜都有明显的缺陷，直到出现了准保角变换法，这种方法兼具了坐标变换法设计灵活和保角变换法参数各向同性的优点，使用也最为广泛[39-56]，在2008年由Pendry和Li在电磁隐身斗篷领域最早提出[39]。从本质上来说，这3种变换方式的理论基础是相通的，并非彼此独立。下面在坐标变换理论基础上简介准保角变换法的原理。

假设变换是在x-y平面进行的，并且电场沿z轴正方向。雅克比矩阵简化为：

带入式(5)可得

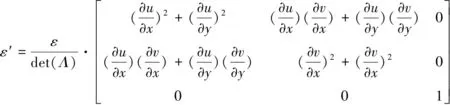
可以看出，变换后的介电常数张量通常呈现强非均匀各向异性。但如果变换函数是保角变换，将柯西-黎曼条件(式(10))带入式(16)，可以将其大大简化为：

.

由于规定电场沿z轴极化，因此对于电磁波传播有贡献的电磁参数只有μxx、μyy和εzz。因此磁导率全部为真空磁导率，介电常数保持各向同性，并且按照εzz所满足的要求分布即可，从而大大降低了对材料电磁参数的要求。

以上简化的前提是变换函数是保角变换，但事实上，在事先已确定好变换区域的情况下，这样严格的保角变换难以找到，但可以通过数值计算的方法找到区域内近似满足保角要求的数值解。根据复变函数理论，如果坐标变换函数满足拉普拉斯方程(式(18))，那么变换就是保角的。

.

因此求取拉普拉斯方程的数值解就可以得到近似满足保角要求的变换函数，从而将参数的各向异性降至最低，这种方法即为准保角变换法。为了求解方程，我们必须给变换区域设置合理的边界条件，通常设置为狄利克雷-纽曼联合边界条件，狄利克雷条件可以将边界上的点固定住，而纽曼条件允许边界上的点沿着边界“滑移”。

4.2 准保角变换透镜的理论设计

在相关研究的基础上，2010年，Kundtz和Smith等人[40]系统阐述了准保角变换法应用于透镜变换领域的具体步骤，并研究设计了将球形的麦克斯韦鱼眼透镜压缩为平板透镜的方法。麦克斯韦鱼眼透镜与龙伯透镜类似，也是一种渐变折射率透镜，透镜表面的任意一点发出的电磁波经过透镜后都可以汇聚到对面的另外一点，其折射率按照下式分布。

式中,r为某点到球心的距离，R为球半径，n0为球心处的介电常数。他们使用Methematica软件求解了区域的拉普拉斯方程，通过画出解的等值线，得到了如图5(a)所示的网格。事实上这些网格的坐标就是变换函数的表现形式，通过适当的运算处理可以得到雅克比矩阵，进而算出介电常数各个分量的空间分布。注意到这些网格是彼此正交的，从而最大限度减小了各向异性。从图5(a)中可以看出，非对角分量μxy接近于0，对角分量εxx和εyy都可近似为1，只是在顶点附近区域略有偏差，这是因为顶点附近区域网格畸变较大，正交性较差。只有εzz在空间中有不同的分布，最大值在7.7左右，在顶点处会出现小于1的值，通常我们将其忽略，修正为1，这样做可以大大减小实现的难度，而且忽略低介电常数的部分对最终结果影响不大。

根据空间各点的一一对应关系，我们可以得到实际空间中介电常数的分布，由于我们忽略了各向异性，因此只需绘制出εzz的分布即可，如图5(b)所示。再乘以麦克斯韦鱼眼透镜本身的介电常数分布(设置式(19)中的n0=2)，我们就得到最终的变换结果(如图5(c)所示)，最大值达到了9.9。

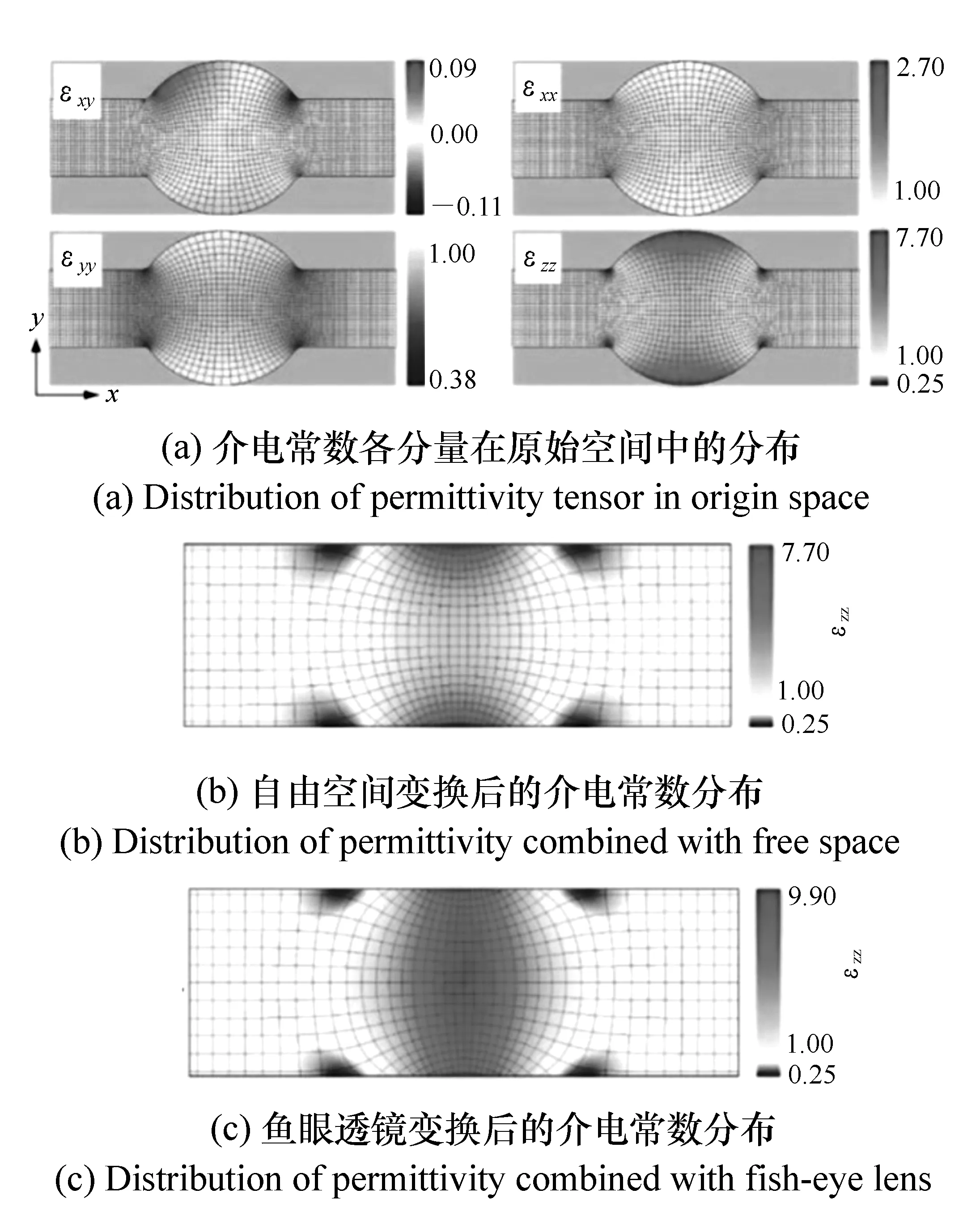
图5 平板麦克斯韦鱼眼透镜[40]Fig.5 Flattened Maxwell fish-eye lens[40]

利用准保角变换法，通过设置适当的变换区域，柏京等[41]将抛物面天线变换为平板透镜天线，得到的天线折射率分布在1到1.25之间(如图6(a)所示)。他们计算得到变换后的透镜天线各向异性因子为1.031 8，可以看作是各向同性的，并使用COMSOL软件对聚焦性能进行了仿真。Wu Qi等人[42]利用准保角变换法，将圆形区域压缩成方形，设计了一种双向准直透镜，放置在透镜中心的线源发出的电磁波经过透镜后可以变为平面波。变换后的透镜折射率分布在1到2.5之间。为了减小由于阻抗不匹配带来的反射，他们还设计了一层厚度为四分之一波长、折射率为1.58的阻抗匹配层，显著提高了方向性系数。在此基础上，他们还通过旋转对称的方式得到了四向准直透镜的折射率分布(如图6(b)所示)。

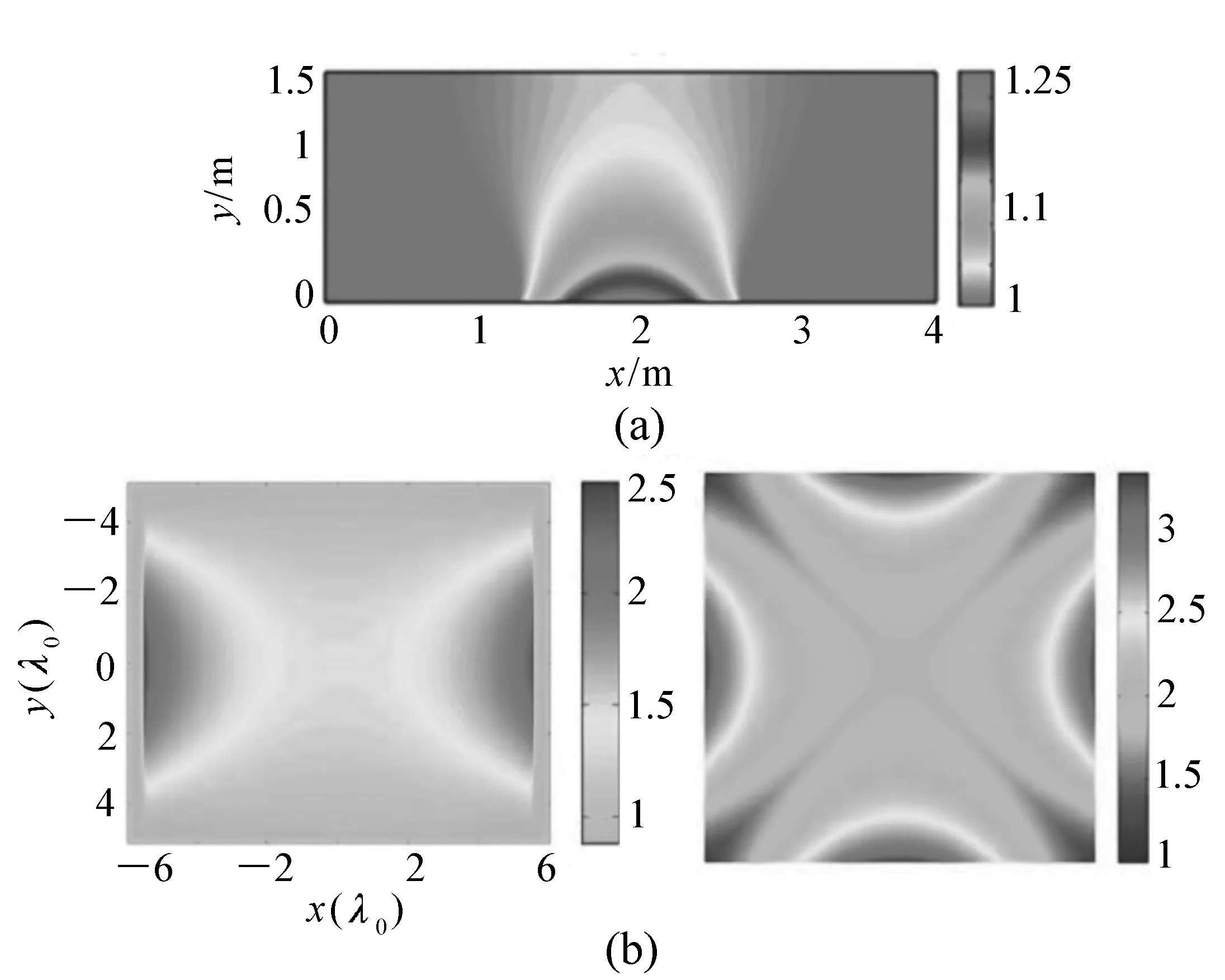
图6 柏京[41](a)和Wu Qi[42](b)设计的透镜折射率分布Fig.6 Index distribution of lenses designed by Bai Jing[41](a) and Wu Qi[42](b)

4.3 准保角变换透镜的实现

准保角变换法得到的介电常数是各向同性的，不要求材料具有磁响应，使用全介电材料即可实现。因此基于准保角变换法设计的透镜不仅限于理论设计，许多研究者采用各种材料和加工技术制备出了新型透镜，其中结合超材料理论设计者居多，这方面最有影响力的两项研究分别来自Kundtz和崔铁军团队，他们的研究成果分别发表在《Nature Material》和《Nature Communication》上。

2009年，Kundtz等人[49]首次采用准保角变换法设计了一种二维龙伯透镜。变换造成的形状变化越大，带来的电磁参数改变就越大。由于他们压缩了半个球体，因此得到的折射率最大值也达到了4.1(如图7(a)所示)。图7(b)所示为透镜样品，他们使用印刷铜微带线的介质单元(如图7(c)所示)制备出透镜，第一次将变换光学透镜设计付诸实践，对后续研究产生了重要的指导意义。但由于这种设计是在二维条件下的，因此应用受到限制。

图7 Kundtz设计的二维压缩龙伯透镜[49]Fig.7 2D flattened Luneburg lens designed by Kundtz[49]

最先制备出三维透镜实物的是崔铁军团队。2010年，他们采用准保角变换法设计了一种工作在Ku波段(12.4～18 GHz)的新型龙伯透镜[50]，折射率分布在1.1至2.1之间(如图8(a)所示)，将分布图绕中心轴旋转，即可得到折射率的三维空间分布。他们选择了FR4(介电常数为4.4)和F4B(介电常数为2.65)两种介质材料，设计了3种带孔方块作为超材料结构单元，这种结构单元是非谐振型的，具有损耗低、工作频带宽的优点。由于超材料单元尺寸应远小于波长，因此他们将方块边长设计为2 mm，约为波长的十分之一。采用等效媒质理论中常用的S参数反演法，计算了上述结构单元的等效折射率，通过改变孔径实现了所需的折射率分布，图8(c)给出了单元结构模型以及等效介电常数随孔径大小的变化规律。他们将透镜分为3个部分，分别打孔加工，最后组合成整体，最终透镜高度104 mm，最大直径108 mm(如图8(b)所示)。对透镜的CST软件仿真和实测结果都表明，这种三维透镜在12.4 GHz到18 GHz的宽带和不同极化条件下具有优异的性能，通过改变馈源位置，可以实现50度范围内的波束扫描。

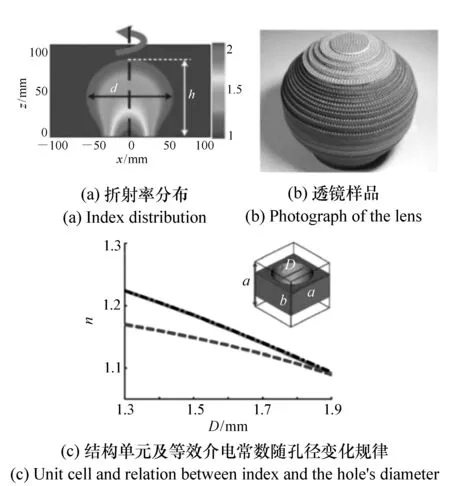
图8 崔铁军设计的三维龙伯透镜[50]Fig.8 3D Luneburg lens designed by Cui Tiejun[50]

同样采用介质材料打孔的方法，Driscoll等人[51]也加工了一种变换龙伯透镜。透镜工作在X波段(8～12 GHz)，变换后的介电常数最大值为3.3，单元结构尺寸约为5 mm，透镜的高度和直径都在20 cm左右。他们使用FR4板和高密度聚乙烯(HDPE)两种材料，通过水喷射切割法进行打孔，制成的透镜如图9所示。

图9 Driscoll设计的三维龙伯透镜[51]Fig.9 3D Luneburg lens designed by Driscoll[51]

李守亮等[53-54]为了提高柱面偶极子天线阵列的辐射性能，采用准保角变换法设计了一种共形透镜天线，工作频率为6 GHz，折射率分布在1.2至2.2之间。图10(a)表示变换前后区域及网格划分，图10(b)表示将变换后的透镜离散为10 mm边长和5 mm边长的正方形。如图10(c)所示，他们以带孔的介质作为结构单元构建了模型，选择的材料为PTFE(聚四氟乙烯，介电常数2.2，损耗角正切0.000 2)。仿真结果表明，共形透镜的存在使得原柱面天线阵的增益提高了2 dB，接近直线天线阵。图10(d)所示为直线阵列、无透镜柱形阵列和有透镜柱形阵列的电场图。

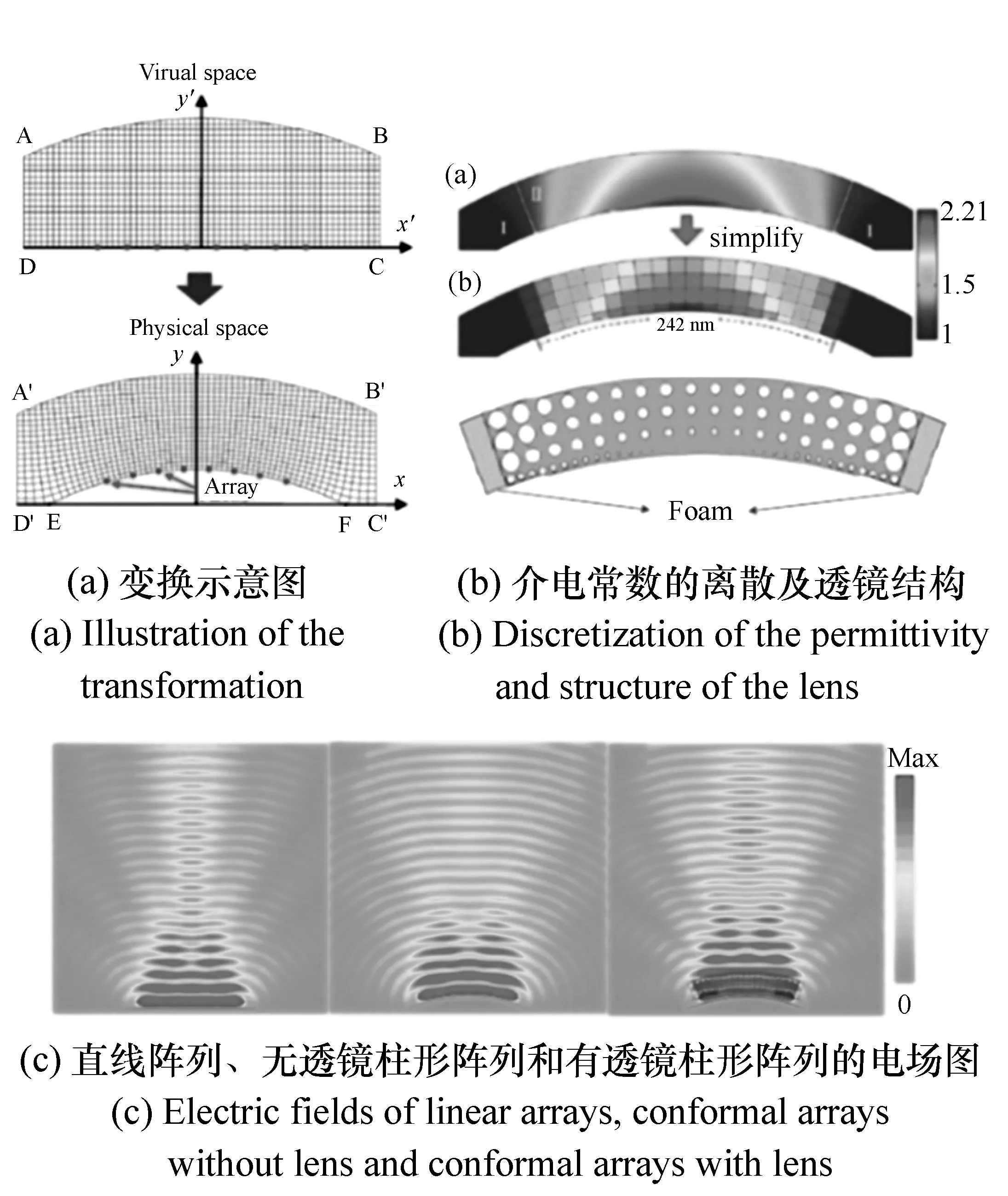
图10 李守亮设计的三维共形透镜[53-54]Fig.10 3D conformal lens designed by Li Shouliang[53-54]

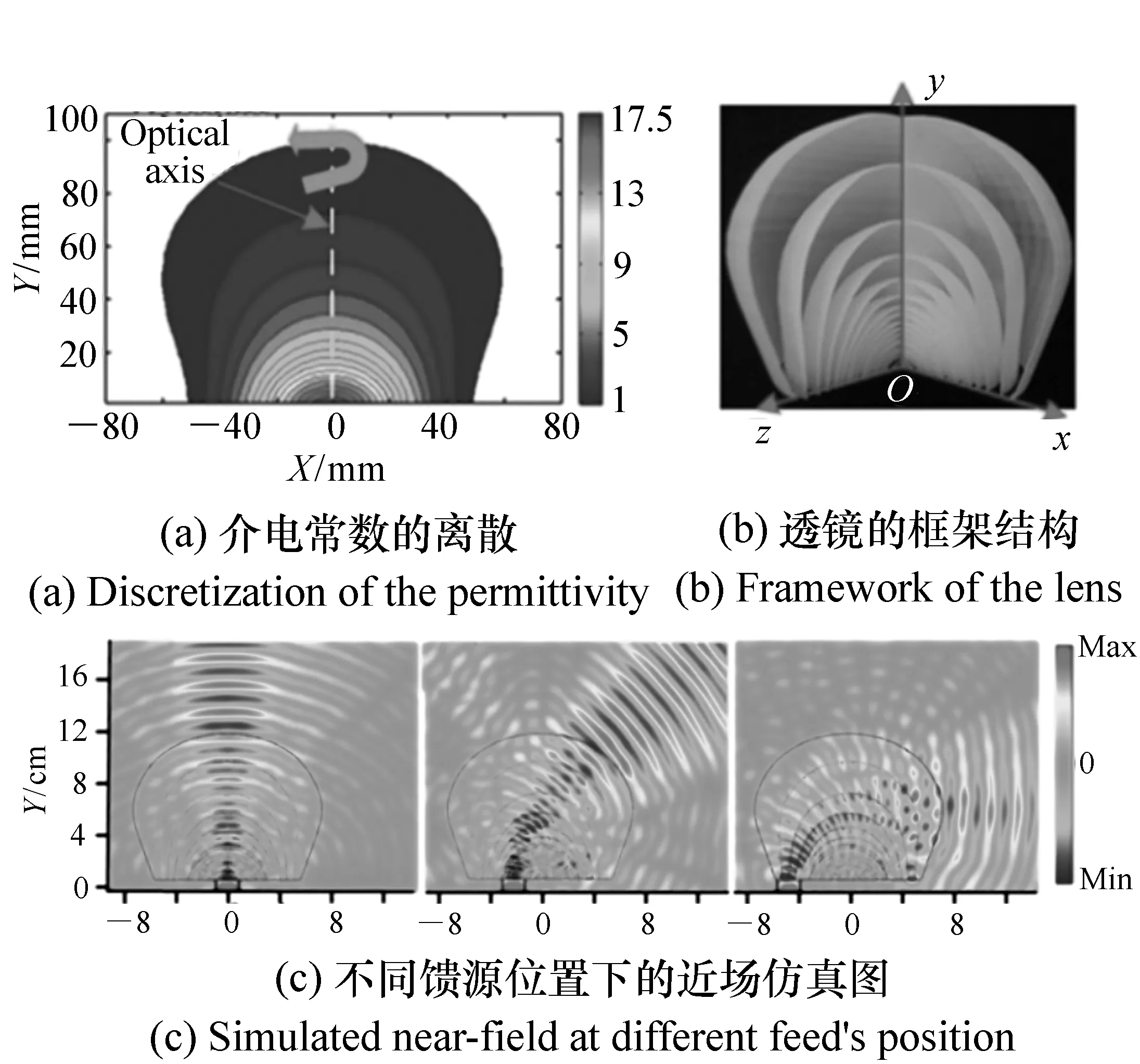
图11 Wu Lingling等设计的液体介质平板龙伯透镜[55-56]Fig.11 Liquid flattened Luneburg lens designed by Wu Lingling[55-56]

由于考虑到透镜的制作，在进行光学变换设计时，折射率可设计的范围往往受材料所限。西安交大的Wu Lingling等人[55-56]巧妙地制作了一种工作在Ku波段的液体介质透镜，通过混合不同比例的苯(介电常数为2.5)和乙腈(介电常数为40)，可以得到不同的介电常数，因此他们设计的透镜介电常数可以比较大，在2.5和17.5之间。在加工时，他们将透镜离散成17层，如图11(a)所示，每层填充不同介电常数的混合介质，层间的球壳采用光敏树脂通过光固化成型技术打印成型，球壳厚度为0.4 mm。图11(b)所示为透镜的框架结构。相比钻孔组装的方法，这种透镜在工业化生产时更为便捷。软件仿真和实测结果都表明，这种透镜可以实现90度的扫描角，图11(c)表示透镜在不同馈源位置下的近场仿真图。

5 结束语

本文详细介绍了基于变换光学方法和超材料理论的新型透镜天线的研究进展，并着重介绍了采用新技术改进龙伯透镜的研究成果。本文将变换光学设计方法归纳为3种：坐标变换法、保角变换法和准保角变换法，阐述了3种方法的基本原理和设计步骤。其中，坐标变换法由于简便直观在早期应用最为广泛，但电磁参数的各向异性是其最大制约，使其只能停留在理论设计阶段；保角变换法虽然得到的参数是各向同性的，但设计困难，研究成果少；而准保角变换法是一种近似满足变换保角要求的数值方法，结合了前述两种方法的优点，具有很好的设计灵活性，并且使用全介电材料即可实现透镜的制备，大大降低了制作难度，因此成为了采用变换光学改进透镜的主要方法。

目前采用准保角变换法结合不同的变换条件设计新型透镜的折射率分布，方法已经比较成熟，也产生了许多新颖的设计成果。在透镜制备方面，人们采用不同材料和不同工艺对加工龙伯透镜进行了尝试，积累了一些经验，但还远远不够。在竞争激烈的天线领域，以龙伯透镜为代表的透镜天线要想获得更多用武之地，必须进一步强化性能优势，减少自身缺陷。

综上所述，变换光学透镜天线在今后的研究方向有：(1)开拓更多适用新型透镜天线的领域和场合，研究设计透镜天线的折射率分布，以超材料理论为主要手段设计结构模型；(2)选择合适的结构—材料—加工工艺体系，研制介电常数适宜、低损耗的材料，提高加工工艺的高效性和可靠性，降低加工成本；(3)实现更小尺寸的超材料单元结构，使得透镜天线的工作频段得以向高频拓展；(4)完善与透镜天线相匹配的馈源系统，满足其他工程应用要求。

[1] 肖雨琴，张英波，李凤山.龙伯透镜天线的研制[J].舰船科学技术,1992,3:33-38. XIAO Y Q,ZHANG Y B,LI F SH. Research on Luneburg lens antenna[J].ShipScienceandTechnology,1992,3:33-38.(in Chinese)

[2] 刘璟.多波束龙伯透镜天线技术研究[D].成都:电子科技大学,2010. LIU J. Study on multi-beam Luneburg lens antenna techniques[D]. Chengdu:University of Electronic Science and Technology of China,2010.(in Chinese)

[3] 钟鸣海.分层龙伯透镜天线技术研究[D].成都:电子科技大学,2009. ZHONG M H. Study on layered Luneburg lens antenna techniques[D]. Chengdu:University of Electronic Science and Technology of China,2009.(in Chinese)

[4] JIANG W X,JESSIE Y C,CUI T J. Anisotropic metamaterialdevices[J].MaterialsToday,2009,12(12):26-33.

[5] SCHUIG D,MOCK JJ,JUSTICE B J,etal.. Metamaterialelectromagnetic cloak at microwave frequencies[J].Science,2006,314(5801):977-980.

[6] MA H F,CUI T J. Three-dimensional broadband ground-plane cloak made of metamaterials[J].NatureCommunication,2010,1(3):605-629.

[7] WERNER D H,KWON D H.TransformationElectromagneticsandMetamaterials[M]. London:Springer,2014.

[8] CHEN H Y,CHAN C T,SHENG P. Transformation optics and metamaterials[J].NatureMaterial,2010,9(5):387-96.

[9] CHEN H Y,HOU B,CHEN S Y,etal.. Design and experimental realization of a broadband transformation media field rotator[J].PhysicalReviewLetters,2009,102(18):183903.

[10] SHU W X,YANG S S,YAN W Y,etal.. Flat designs of impedance-matchednon magnetic phase transformer and wave-shaping polarization splittervia transformation optics[J].OpticsCommunications,2014,338:307-312.

[11] CHEN C,LIU S B,WANG S Y. A shifted waveguide connector combinedwitha photonic crystal filter designed by transformationoptics[J].Optics&LaserTechnology,2013,49(49):161-165.

[12] PENDRY J B,SCHUIG D,SMITH D R. Controlling electromagnetic fields[J].Science,2006,312:1780-1782.

[13] LEONHARDT U. Optical conformal mapping[J].Science,2006,312:1777-1780.

[14] 蒋卫祥.变换光学及其应用[D].南京:东南大学,2010. JIANG W X. Transformation optics and its applications[D]. Nanjing:Southeast University,2010.(in Chinese)

[15] 张永亮，董贤子，段宣明，等.变换光学的物理原理和前沿进展[J].量子电子学报,2014,31(4):385-393. ZHANG Y L,DONG X Z,DUAN X M,etal..Fundamental and frontiers of transformation optics[J].ChineseJ.QuantumElectronics,2014,31(4):385-393.(in Chinese)

[16] 陈曦.超材料的电磁特性与应用研究[D].长沙:国防科学技术大学,2013. CHEN X. Research on the electromagnetic characters and applications of metamaterial[D]. Changsha:National University of Defense Technology,2013.(in Chinese)

[17] 张检发，袁晓东，秦石乔.可调太赫兹与光学超材料[J].中国光学,2014,7(3):349-364. ZHANG J F,YUAN X D,QIN SH Q. Tunable terahertz and optical metamaterials[J]. Chinese Optics,2014,7(3):349-364.(in Chinese)

[18] 贾秀丽，王晓鸥，周忠祥，等.手性负折射率材料的最新进展[J].中国光学,2015,8(4):548-556. JIA X L,WANG X O,ZHOU ZH X,etal.. Latest progress on chiral negative refractive index metamaterials[J].ChineseOptics,2015,8(4):548-556.(in Chinese)

[19] 张会，张卫宇，徐旺，等.THz波段光子晶体带隙影响因素研究[J].发光学报,2012,33(8):883-887. ZHANG H,ZHANG W Y,XU W,etal.. Study on the influencing factors of photonic crystal′s band gaps in THz waveband[J].ChineseJ.Luminescene,2012,33(8):883-887.(in Chinese)

[20] 庞永强.电磁吸波超材料理论与设计研究[D].长沙:国防科学技术大学,2013. PANG Y Q. The theory and design of metamaterialabsorbers[D]. Changsha:National University of Defense Technology,2013.(in Chinese)

[21] MA H F,CHEN X,YANG X M,etal..A broadband metamaterial cylindrical lens antenna[J].ChineseScienceBulletin,2010,55(19):2066-2070.

[22] ABDALLAH D,SHAH N B,ANDRE D L,etal..Compact metamaterial-based substrate-integrated Luneburg lens antenna[J].AntennasandWirelessPropagationLetters,2012,11(4):1504-1507.

[23] XUE L,FUSCO V F. 24 GHz automotive radar planar Luneburg lens[J].Microw.Antennas.Propag,2007,1(3): 624-628.

[24] 刘志佳.基于开孔结构的龙伯透镜天线技术[D].成都:电子科技大学,2011. LIU ZH J. Techniques of Luneburg lens antenna based on drilled holes structure[D]. Chengdu:University of Electronic Science and Technology of China,2011.(in Chinese)

[25] MIN L,NG W R,CHANG K H,etal.. An X-band luneburg lens antenna fabricated by rapid prototyping[J].IEEEMTT-SInternationalMicrowaveSymposium,2011:1-4.

[26] 田小永，殷鸣，李涤尘.渐变折射率人工电磁介质设计与3D打印制造[J].机械工程学报，2015(7):124-129. TIAN X Y,YIN M,LI D C. Design and fabrication of gradient index artificial electromagnetic medium based on 3D printing[J].J.MechanicalEngineering,2015(7):124-129.(in Chinese)

[27] KONG F M,WU B L,KONG J A,etal..Planar focusing antenna design by using coordinate transformation technology[J].AppliedPhysicsLetters,2007,91(25):253509-3.

[28] KWON D H,WERNER D H. Transformation optical designs for wave collimators,flat lenses and right-angle bends[J].NewJ.Physics,2008,10(11):1005-1008.

[29] JIANG W X,CUI T J,MA H F,etal.. Cylindrical to planewave conversion via embedded optical transformation[J].AppliedPhysicsLetters,2008,92(26):261903-3.

[30] JIANG W X,CUI T J,MA H F,etal.. Layered high-gain lens antennas via discrete optical transformation[J].AppliedPhysicsLetters,2008,93(22):221906-3.

[31] HUANG L J,WANG Z Q,ZHOU S T,etal.. A novel design for high gain lens antennas with homogeneous media[J].PhotonicsandNanostructures-FundamentalsandApplications,2012,10(4):615-623.

[32] YAO K,JIANG X Y,CHEN H Y. Collimating lenses from non-euclidean transformationoptics[J].NewJ.Physics,2012,14(2):23011-23019.

[33] ZHANG J J,LUO Y,XI S,etal.. Directive emission obtained by coordinate transformation[J].ProgressinElectromagneticsResearch,2008,81(81):437-446.

[34] LUO Y,ZHANG J J,CHEN H S,etal..High-directivity antenna with small antenna aperture[J].AppliedPhysicsLetters,2009,95(19):193506-3.

[35] TICHIT P H,BUROKUR,LUSTRAC A D. Ultradirective antenna via transformation optics[J].J.AppliedPhysics,2009,105(10):104912-6.

[36] TURPIN J P,MASSOUD A T,JIANG Z H,etal..Conformal mappings to achieve simple material parameters for transformation optics devices[J].OpticsExpress,2010,18(18):244-252.

[37] YAO K,JIANG X Y. Designing feasible optical devices via conformal mapping[J].J.OpticalSocietyofAmericaB,2011,28(5):1037-1043.

[38] 刘佳.超材料在光学传输方面的应用研究[D].南京：南京航空航天大学,2014. LIU J. Application of metamaterial in optical transmission[D]. Nanjing:Nanjing University of Aeronautics and Astronautics,2014.(in Chinese)

[39] LI J,PENDRY J B. Hiding under the carpet: a new strategy for cloaking[J].PhysicalReviewLetters,2008,101(20):2952-2965.

[40] SMITH D R,URZHUMOV Y,KUNDTZ N B,etal.. Enhancing imaging systems using transformation optics[J].OpticsExpress,2010,18(20):21238-21251.

[41] MEI Z L,BAI J,NIU T M. A planar focusing antenna designed using quasi-conformal mapping[J].ProgressinElectromagneticsResearchM,2010,13(2):261-273.

[42] WU Q,TUIPIN J,TANG W X,etal.. Flat collimating lenses based on quasi-conformal transformation electromagnetics[C]. European Conference on Antennas and Propagation.IEEE,2012:1696-1700.

[43] KWON D H. Quasi-Conformal transformation optics lenses for conformal arrays[J].IEEEAntennas&WirelessPropagationLetters,2012,11(12):1125-1128.

[44] AGHANEJAD I,ABIRI H,YAHAGHI A. Design of high-gain lens antenna by gradient-index metamaterialsusing transformation optics[J].IEEETransactionsonAntennas&Propagation,2012,60(9):4074-4081.

[45] WU Q,JIANG Z H,TERUEL O Q,etal.. Transformation optics inspired multibeamlens antennas for broadband directive radiation[J].IEEETransactionsonAntenna&Propagation,2013,61(12):5910-5922.

[46] CHANG Z,ZHOU X M,HU J,etal.. Design method for quasi-isotropic transformation materials based on inverse Laplace's equation with sliding boundaries[J].OpticsExpress,2010,18(6):6089-6096.

[47] TANG W X,ARGYROPOULOS C,KALLOS E,etal.. Discrete coordinate transformation for designing all-dielectric flat antennas[J].IEEETransactionsonAntennas&Propagation,2011,58(12):3795-3804.

[48] SEGURA C M,DYKE A,DYKE H,etal.. Flat Luneburg lens via transformation optics for directive antenna applications[J].IEEETransactionsonAntennas&Propagation,2014,62(4):1945-1953.

[49] KUNDTZ N,SMITH D R. Extreme-angle broadband metamateriallens[J].NatureMaterials,2010,9(9):129-132.

[50] MA H F,CUI T J. Three-dimensional broadband and broad-angle transformation-optics lens[J].NatureCommunication,2010,1(8):173-184.

[51] DRISCOLL T,LIPWORTH G,HUNT J,etal..Performance of a three dimensional transformation-optical-flattened Luneburg lens[J].OpticsExpress,2012,20(12):13262-13273.

[52] YANG R,TANG W X,HAO Y. A broadband zone plate lens from transformation optics[J].OpticsExpress,2011,19(19):12348-12355.

[53] LI S L,ZHANG Z,WANG J H,etal.. Design of conformal lens by drilling holes materials using quasiconformal transformation optics[J].OpticsExpress,2014,22(21):25455-25465.

[54] 李守亮.变换电磁学在天线设计中的应用研究[D].北京：北京交通大学,2015. LI SH L. Research of transformation electromagnetic theory applied to antenna design[D]. Beijing:Beijing Jiaotong University,2015.(in Chinese)

[55] WU L L,TIAN X Y,MA H F,etal.. Broadband flattened Luneburg lens with ultra-wide angle based on a liquid medium[J].AppliedPhysicsLetters,2013,102(7):074103-4.

[56] WU L L,TIAN X Y,YIN M,etal.. Three-dimensional liquid flattened Luneburg lens with ultra-wide viewing angle and frequency band[J].AppliedPhysicsLetters,2013,103(8):084102-4.

Research progress of transformation optics lens antenna

CAO Shang-wen, ZHOU Yong-jiang*, CHENG Hai-feng

(ScienceandTechnologyonAdvancedCeramicFibersandCompositesLaboratory,NationalUniversityofDefenseTechnology,Changsha410073,China)

*Correspondingauthor,E-mail:zyj.ly@163.com

Luneburg lens antenna is a kind of gradient index lens antenna, but its application is restricted due to certain disadvantages. In recent years, various new-type lens antennas, the most representative of which was planar Luneburg lens, were designed by means of transformation optics and metamaterial theories. In this paper, three transformation optics techniques of lens design including coordinate transformation, conformal mapping and quasi-conformal mapping are summarized and compared. Quasi-conformal mapping has better research and application prospect because of its flexibility in lens design and easy fabrication by all dielectric materials. Principles and procedures of quasi-conformal mapping in lens design are elaborated, and important research fruits about lens transformation and fabrication are introduced. Finally, the research directions of transformation optics lens antenna in the future are proposed.

lens antenna;Luneburg lens;transformation optics;metamaterial;quasi-conformal mapping

2016-10-21；

2016-11-25

2095-1531(2017)02-0164-12

O431.1； TB34

A

10.3788/CO.20172002.0164

曹尚文(1992—)，男，山东济宁人，硕士研究生，2014年于国防科技大学获得学士学位，主要从事人工电磁材料方面的研究。E-mail:caoshangw@163.com

周永江(1976—)，男，湖南浏阳人，副研究员，硕士生导师，2006年于国防科技大学获得博士学位，主要从事微波功能材料方面的研究。E-mail: zyj.ly@163.com