基于负载均衡的MVB周期数据调度优化

王保华，严　翔，王立德, 王　昕

(1.北京交通大学 电气工程学院，北京　100044；2.中国铁道科学研究院 机车车辆研究所， 北京　100081)

列车级别的总线WTB(Wire Train Bus)用于连接动态编组的列车，车辆级别的总线MVB(Multifunction Vehicle Bus)用于车辆内部各设备之间的连接[1-4]。MVB网络采用主从方式对总线设备进行集中控制，由唯一的总线管理器采用非抢占性的方式，通过轮询内置的周期扫描表，管理和安排各个从设备的通信过程。

文献[5]提出了同步的单调速率(Rate Monotonic，RM)调度算法，但此方法构建的周期扫描表过于庞大，容易增加系统的开销。文献[6]在此基础上做了更为深入地研究，给出了基于约束条件构建周期扫描表的RM调度算法方法，有效地减小了调度表的规模。为更好地建立周期扫描表，更加合理地对MVB网络通信过程进行调度，国内外的研究人员对RM调度算法进行了优化。文献[7]为了能够将周期扫描表内的负载均匀分布，提出了混合遗传优化算法，此算法的目标是降低周期扫描表的宽度和陡度。文献[8]采用粒子群算法建立周期扫描表，该算法为了达到“均衡总体、异化个体”的目的，选用了多个优化目标，但该方法存在出现早熟收敛和陷入局部最优的危险。文献[9]提出对于传输数据量最大的端口，其数据传输安排在当前网络负荷最小的基本周期内进行，从而实现周期扫描表中周期变量的均匀分布，达到负载均衡的目的；但是此方案只在网络负荷较低的情况下适用，一旦网络负荷增多，将出现最小的基本周期和特征周期不匹配的情形。文献[10]分析了CRH3型高速动车组周期轮询策略存在总线负载利用率不均匀和周期负载占用带宽相差较大等不足，提出了基于周期扫描表的总线负载率均匀度优化算法，但是该算法的多个约束条件使得其适用范围过小。尽管以上各种算法对RM调度算法进行了许多优化，如有的设计了多个优化目标，有的则设置了多个约束条件，但是也增加了优化算法的复杂程度，限制了它们的推广应用。

本文采用以负载不均衡度最小为单一目标的免疫遗传算法，建立MVB网络周期扫描表，同时基于预测域方法进一步降低算法的复杂度，最后通过仿真和试验验证算法的可行性。

1　问题描述

1.1　MVB周期通信模型

如果MVB网络管理着多个从设备，假设在整个网络通信过程中共有N个周期信息需要进行调度，那么可将周期信息通信任务抽象为1个集合P，为

P={P1，P2，…，PN}

(1)

第i个周期信息通信任务Pi为

Pi=(Ti，Li，φi)i∈{1，2，…，N}

(2)

式中：Ti为特征周期，ms；Li为报文长度，μs；φi为初相，是第i个周期信息第1次开始通信时基本周期的编号。

1.2　传统周期扫描表构建方法的缺陷

MVB网络进行报文传输时，在某个时刻MVB网络主设备会发出1个主帧，网络中某个从设备的地址如果恰好匹配此主帧中的目的地址，则会做出响应，发出1个从帧。主设备按照周期扫描表的规定对从设备进行依次轮询。

(1)基本周期Tbp：指MVB网络主设备发起轮询的最小单位时间，为

1 ms≤Tbp≤2.5 ms

(3)

(2)特征周期Tip：指周期信息的数据被轮询1次的时间，它是基本周期的2λ倍，但按照规定，特征周期不能大于210倍的基本周期，即不能大于1 024 ms，则

Tip=2λTbpλ∈{0，1，…，10}

(4)

(3)宏周期TMp：指所有特征周期中最长的那个，也是周期扫描表的循环周期，即

TMp=max{Tip}

(5)

(4)负载率η：指某基本周期内K个有效报文的总时间占整个基本周期的比值，即

(6)

(7)

式中：si为第i个周期信息的特征周期对于基本周期的倍数。

以6个周期信息的通信任务(各项参数见表1)为例，根据MVB的协议标准，规定其主帧的报文长度由功能码决定。采用传统构建周期扫描表的RM调度算法可以快速生成周期扫描表[5]，结果见表2。表中：1表示此处某个周期信息需要发送数据；0表示不发送。

从表2可以看出：网络负载分配的结果非常不均匀，负载率的最大值约为最小值的3倍；若将P5的初相从2调整为4，将P6的初相从3调整为8，就能更好地实现负载率的均衡分布，由此可以看出初相是决定负载率均衡分布的关键因素。

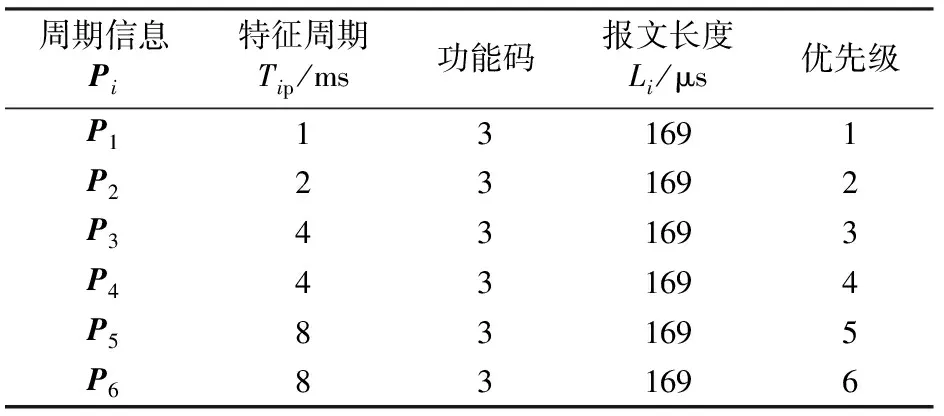
表1　周期信息各项参数

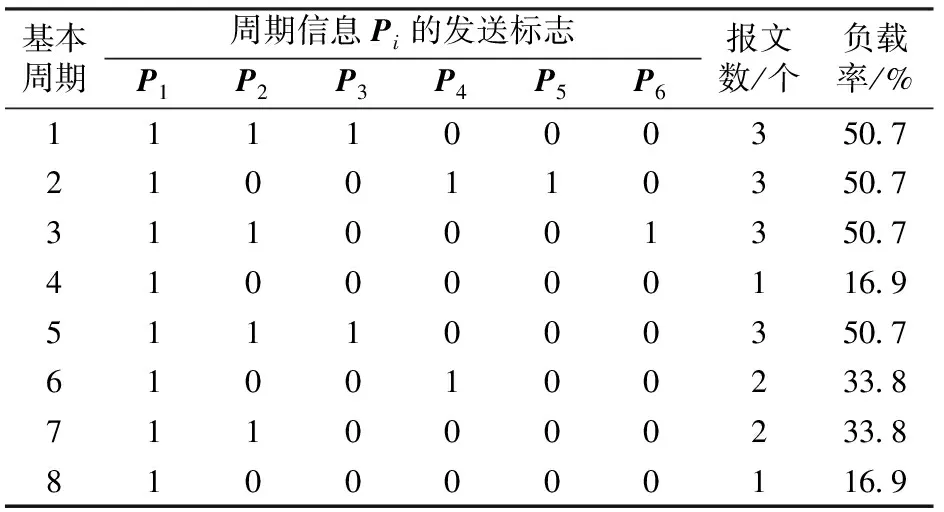
表2　周期扫描表

正如很多文献中描述的那样，采用TCN标准推荐的RM调度算法生成周期扫描表，虽然算法简单，但并不能达到最优的结果，而且随着报文长度的增加，这种不平衡的情况会更加严重[11]。而且由于目前国内铁路机车尤其是动车组的列车网络中控制设备较多，网络通信负载较大，采用简单的RM调度算法进行周期扫描表的构建很难满足要求，需要研究新算法对扫描表的构建过程进行相应的优化。

2　优化模型及算法构建

2.1　基于负载均衡的优化模型

对于1个已经确定的MVB网络，如果周期信息的特征已经确定，那么第i个周期信息Pi的特征周期和报文长度也是固定的。由于初相φi是负载率均衡分布最关键的影响因素，因此所有的初相组成初相向量Φ=(φ1,φ2, …,φN)。如果我们能找到一组初相Φ，使得整个宏周期内的周期信息均匀分布，那么就可以达到负载率均衡分布的优化目标。

当1组周期信息参数给定之后，它们的宏周期就是确定的，且经过计算所得的平均负载率也是不变的。此时，可以将整个宏周期内每个基本周期的负载θ作为1组考察数据，它们相互之间的波动程度可以用这组数据的标准差(负载不均衡度)σ衡量。因此，可以以这个标准差构建优化目标函数fEq(Φ)，即

fEq(Φ)=σ(θ1，θ2， …，θk， …，θM)=

(8)

式中：M为基本周期的数量；k为基本周期的序号;l为周期信息在某个基本周期内的序号；Lkl为第k个基本周期内第l个周期信息的长度；rk为第k个基本周期内有效周期信息的总数。

由式(8)可以看出：寻找全局最优解即寻找1组最优初相分配达到负载率均衡分布的过程，进一步可以转化为寻找最小的基本周期负载标准差即负载不均衡度fEq的过程。也就是说fEq越小，最终生成的周期扫描表可使负载将更加均衡。这显然是1个组合最优化的问题，并且采用单一的目标函数进行优化可使算法过程将更加清晰。为了提高计算效率，采用改进的免疫遗传算法对此进行求解。

2.2　基于预测域的免疫遗传算法

遗传算法(Geneitc Algoirthm，GA)提供了1种搜索最优解的计算模型，它具有功能强、鲁棒特性好等优点，并且计算简单，已被广泛应用于很多领域解决一些实际问题[12-14]。随着遗传算法以及粒子群算法等优化算法在越来越多的领域使用，它们的一些缺点也逐渐显现，例如早熟收敛、过早陷入局部最优等问题。为了改进算法，Chun等[15]提出了1种免疫遗传算法(Immune Genetic Algorithms，IGA)，它将免疫理论和基本遗传算法的优点结合起来，使得求解过程类似生物免疫调节的过程，如果抗体的 “浓度”过高，容易发生早熟收敛时，就对高“浓度”的抗体进行抑制。针对MVB网络，单个抗体为周期信息的1组初相向量，抗体浓度与优化目标函数即各个基本周期负载的标准差相关，则第n个抗体的浓度Cn为

(9)

式中：Q为原抗体群中抗体的数量；R为抗体的新增数量。

由式(9)可得抗体的复制概率Pn为

(10)

根据式(10)所计算出的概率对抗体群中的抗体进行选择复制，形成新的抗体群,这样能够使新抗体群中的抗体保持一定的差异性，从而避免早熟收敛的发生。

(11)

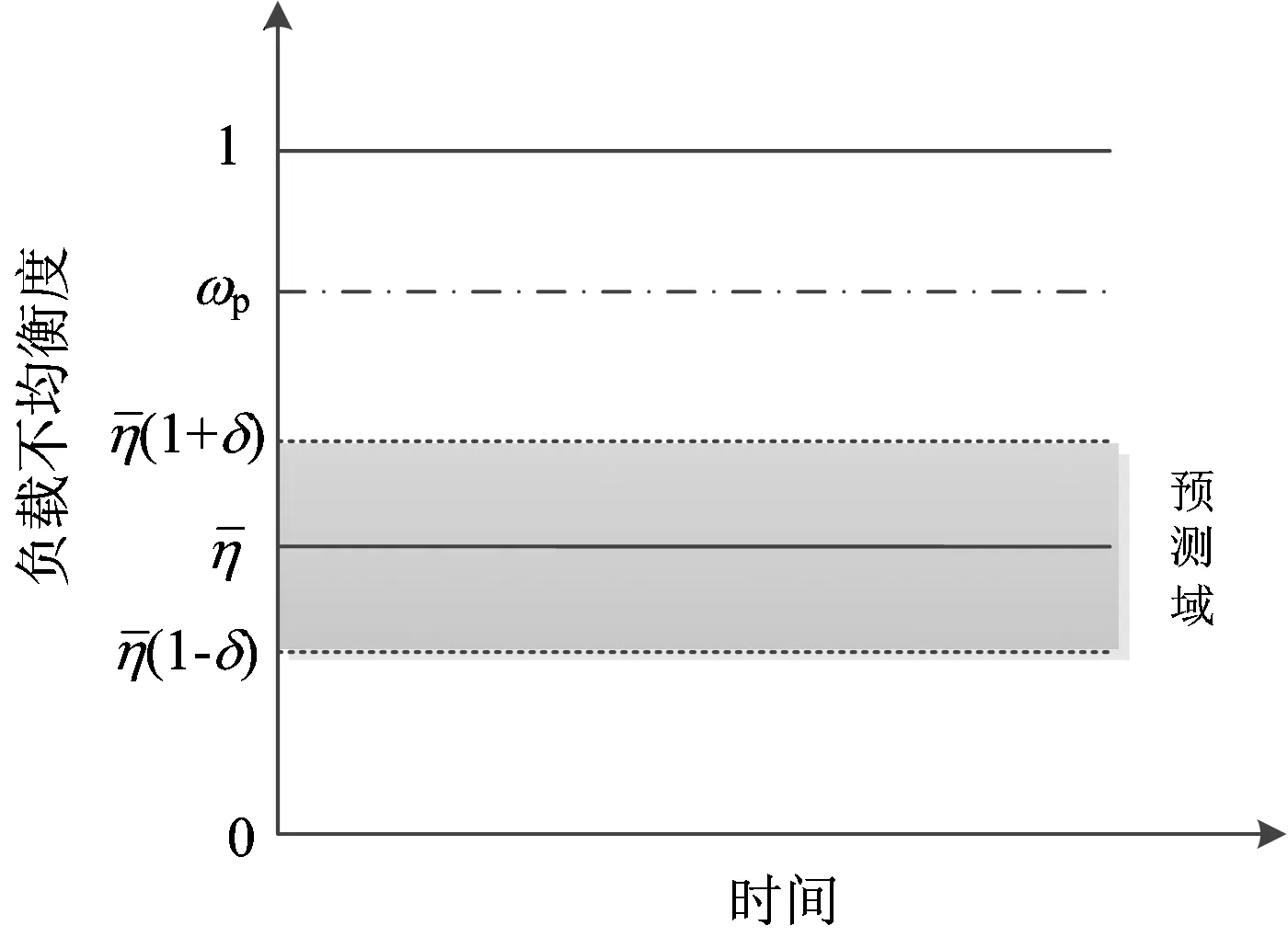
图1　预测域示意图

本文在标准免疫遗传算法的基础上，引入了以平均负载率为中心的预测域，在确定的范围内有选择地进行族群进化，使优化目标更加明确，使寻找全局最优解的过程更快，大大提高优化算法的收敛速度。本文优化算法流程如图2所示。

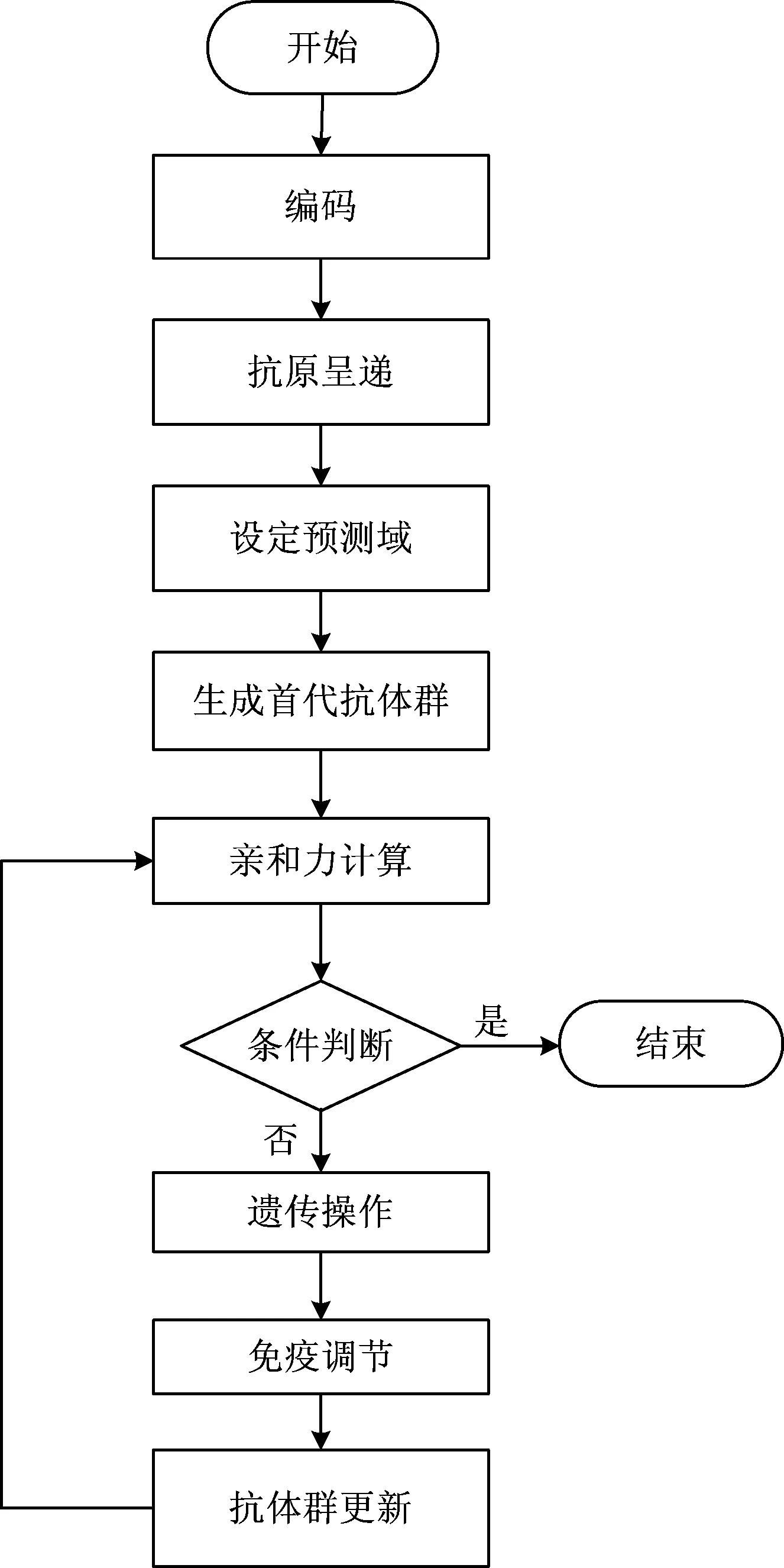
图2　本文优化算法流程图

步骤2：抗原呈递。将ωp和fEq(Φn)共同作为算法的抗原，其中周期相比例ωp的约束条件为

(12)

步骤4：生成首代抗体群。随机生成Q个抗体，由它们组成首代父抗体群X0。

步骤5：计算亲和力。因为fEq(Φn)越小，抗体越好，所以使用B-fEq(Φn)表示抗体和抗原之间的亲和力(B为大于零的常量)。计算过程中如果发现精英抗体则存入记忆库，否则把亲和力最优的抗体存入记忆库。

步骤6：终止条件判断。若当前抗体群Xu满足条件，则转步骤10；否则转步骤7。

步骤7：遗传操作。对当前父抗体群Xu进行交叉和变异，其中交叉概率和变异概率预先设定。

步骤8：免疫调节。重新随机生成R个新的抗体，根据式(10)的计算结果在Q+R中选取Q个抗体建立中间抗体群Yu。

步骤9：抗体群更新。对中间抗体群Yu进行选择操作形成新一代的抗体群Xu+1，具体过程是：将抗体群Yu中较差的抗体剔除，并取出记忆库中优质的抗体加入，然后转步骤5。

步骤10：输出最优初相向量和对应的目标函数值作为最终结果，算法终止。

3　试验及结果分析

3.1　仿真验证

使用Matlab软件，以文献[7]中的算例对算法进行仿真验证。在此算例中共有20个源端口的周期信息，它们的各项参数见表3。特征周期越小的通信任务越需要优先处理，因此依据特征周期从小到大的顺序对周期信息进行排序，若特征周期相等，则按照MVB网络功能码由大至小进行排序。

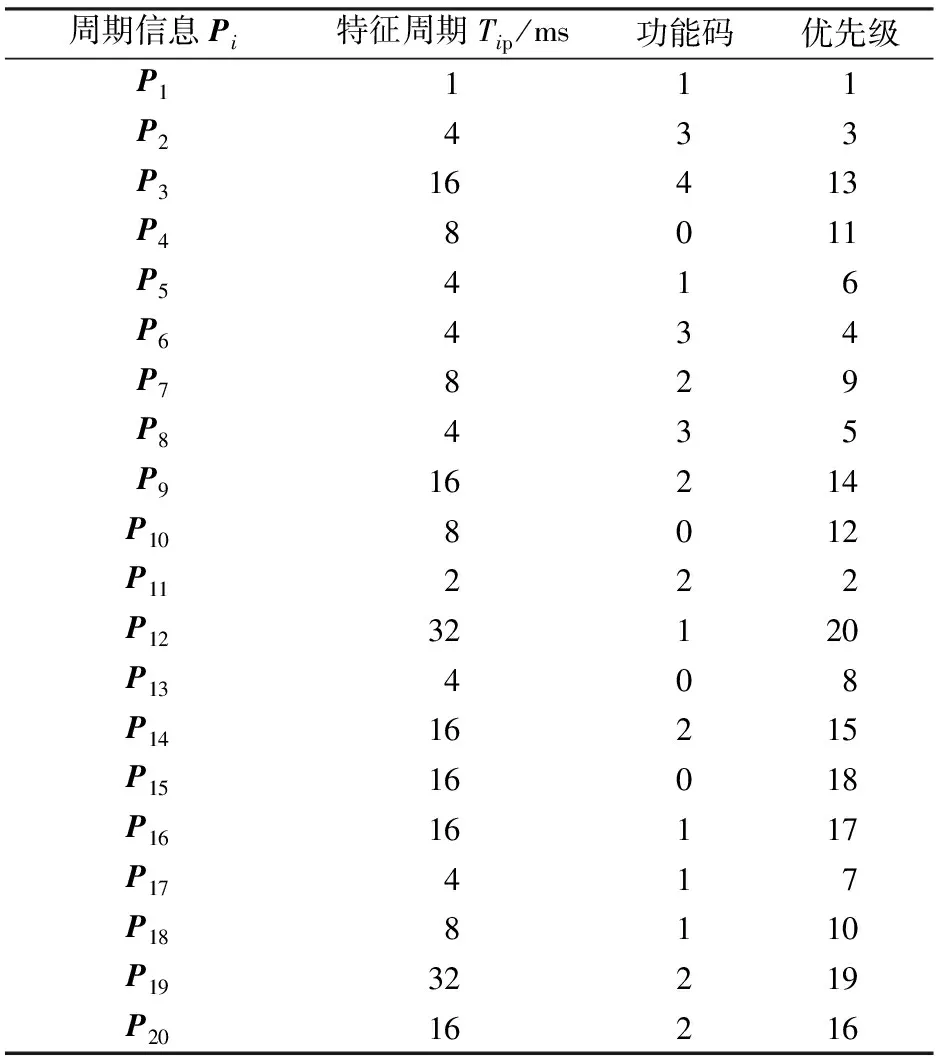
表3　周期信息参数表

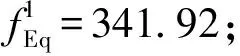
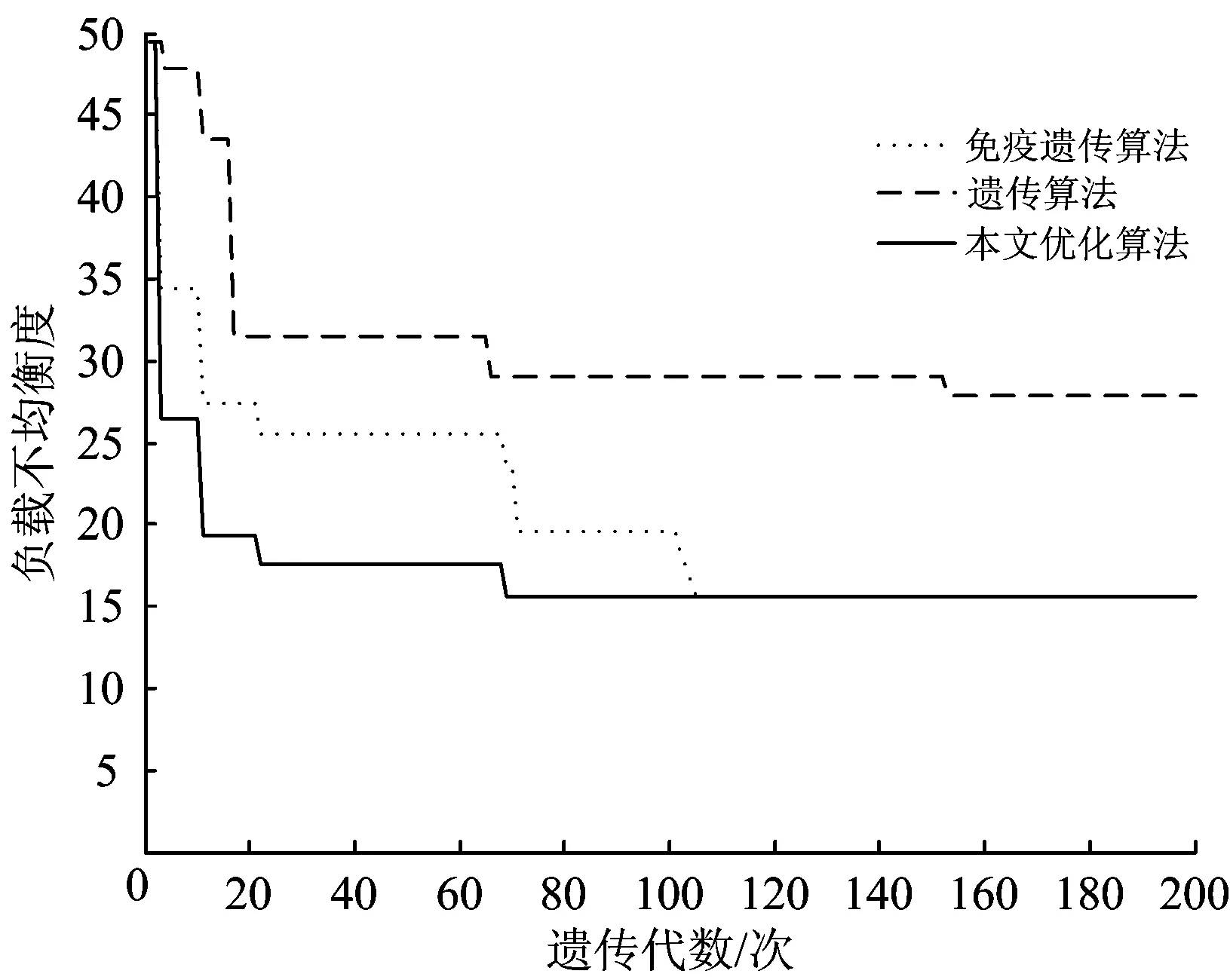
图3　进化过程

同时图3中还给出了遗传算法和免疫遗传算法的负载均衡度进化过程。从图3可以看出：相较于其他2种算法，本文优化算法的收敛速度最快，能够顺利地收敛到全局最优解，且没有陷入局部最优。

表4通过总线占用率对3种算法进行了对比分析。从表4可以看出：用RM调度算法建立的周期扫描表其负载均衡度是最差的，本文和文献[7]的优化算法都能够获得1个较好的结果，但本文优化算法的收敛速度更快，最优解也更优。虽然本文算法的复杂度较RM调度算法高，但是由于加入了预测域的限制，其复杂度较其他优化算法仍降低很多。

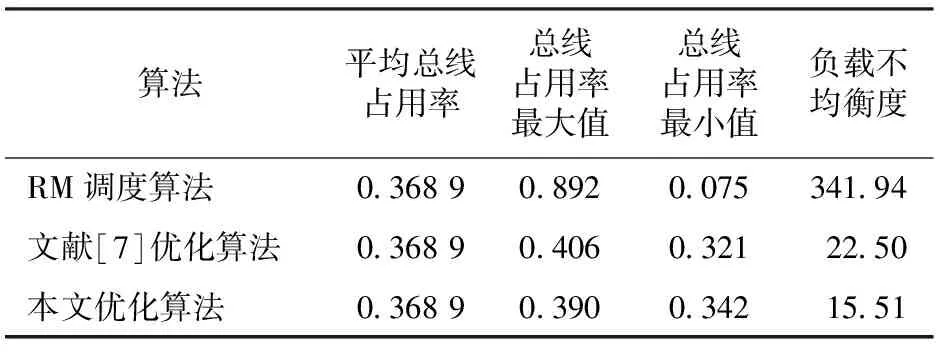
表4　总线占用率对比

3.2　试验验证

为了进一步验证本文算法，搭建了基于MVB网络的实时信息周期负载率测试试验平台，其拓扑结构如图4所示。其中有1个主设备和3个从设备，另外还有一个协议分析仪，用于实时监听和采集总线数据。

试验中采用与仿真验证同样的算例， 其4个主、从设备的地址及20个周期信息分别对应的源端口见表5。

图4　MVB网络的实时信息周期负载率测试试验拓扑结构

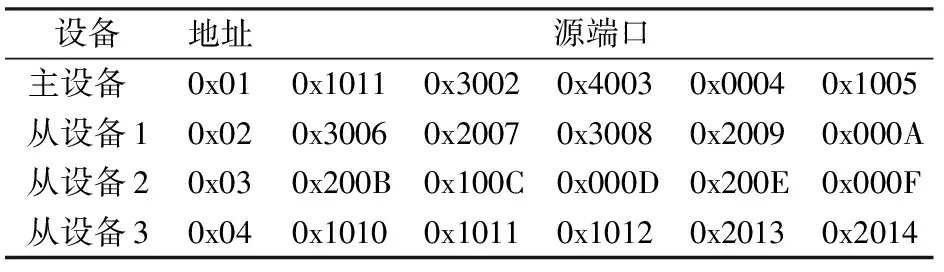
设备地址源端口主设备0x010x10110x30020x40030x00040x1005从设备10x020x30060x20070x30080x20090x000A从设备20x030x200B0x100C0x000D0x200E0x000F从设备30x040x10100x10110x10120x20130x2014

另外，试验设置基本周期为1 ms，周期相比例ωp为90%，宏周期为32 ms，其他参数不变。分别用RM调度算法、文献[7]优化算法以及本文优化算法得到周期扫描表后，配置此平台下MVB网络的参数，然后进行连续20 min的网络通信试验，得到1个宏周期即0.2 s内网络负载率变化的对比情况，如图5所示。

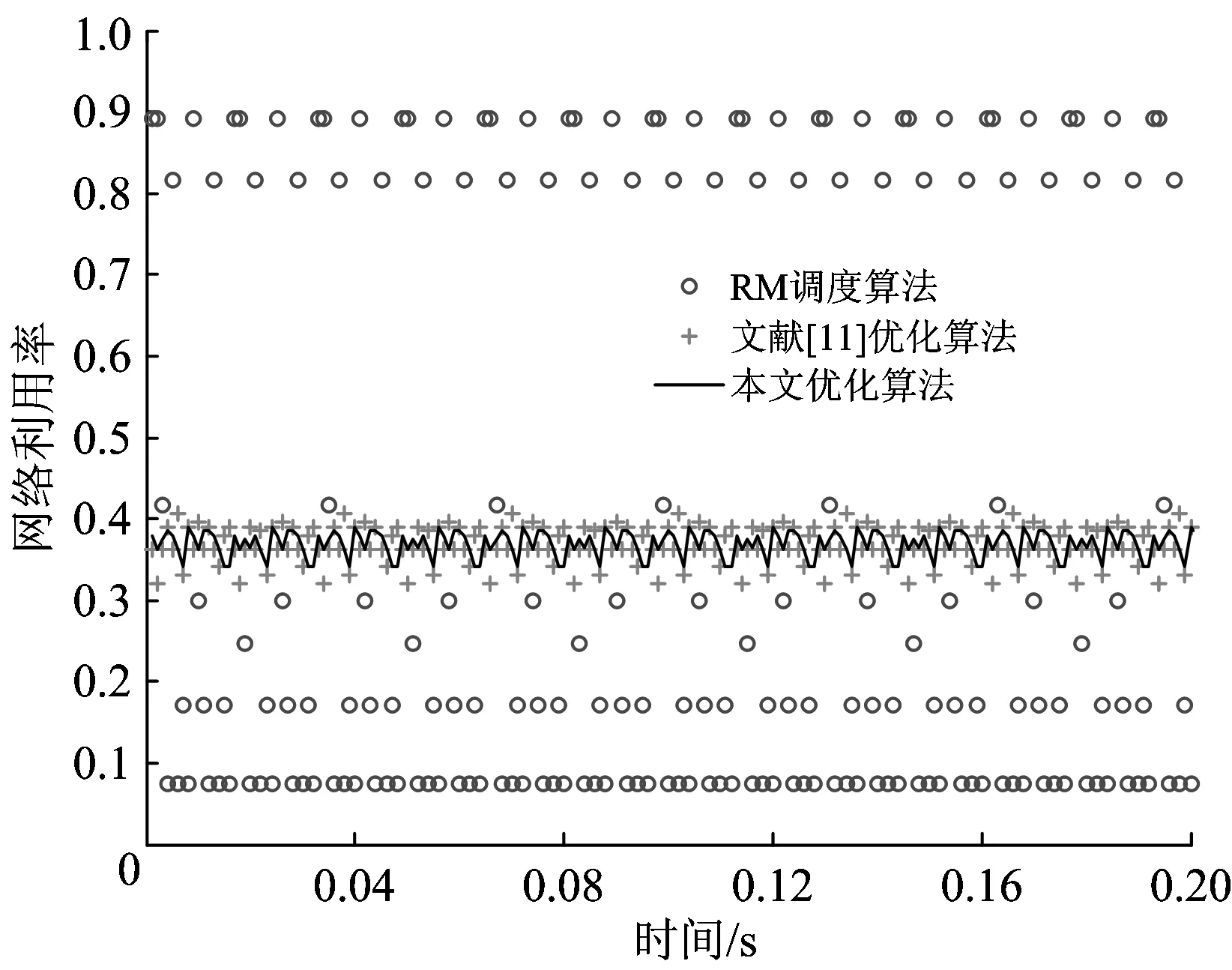
图5　3种优化算法的结果比较

由图5可以看出：采用RM调度算法时MVB网络的负载有很大的波动性，即MVB网络的负载均衡度非常差，且当网络负荷较高时很容易出现数据丢包以及网络不可调度的状况；采用文献[7]优化算法和本文算法时结果均好，而且采用本文算法得到的结果相对更加稳定，对于承载更多的网络负荷有很大帮助，试验结果与仿真结果一致，证明了本文算法的有效性。

4　结　语

研究和分析了用RM调度算法构建周期扫描表的方法，发现其很难实现负载均衡分配，对MVB通信性能产生较大的影响。本文将负载不均衡度最小作为单一的优化目标建立优化模型，再采用基于预测域的免疫遗传算法进行全局最优求解。算例的仿真和试验结果表明，本文优化算法能够更快地收敛到全局最优解，使MVB网络负载的均衡，从而有利于基于MVB的列车控制网络容纳更多的子系统，提升系统的服务指标。

[1]JIMENEZ J, MARTIN J L, ZULOAGA A, et al.Comparison of Two Designs for the Multifunction Vehicle Bus[J]. IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems, 2005, 25(5): 797-805.

[2]UNZUETA H, JIMENEZ J, MARTIN J L, et al. An Emulator to Develop the Wire Train Bus Protocol Stack [C]//IECON 2006-2nd Annual Conference on IEEE Industrial Electronics.Paris:IEEE, 2006: 4225-4230.

[3]IEC. IEC61375-1 Electric Railway Equipment Train Bus Part1: Train Communication Network[S]. Geneva: IEC, 1999.

[4]JIMENEZ J, MARTIN J L, BIDARTE U, et al. Design of a Master Device for the Multifunction Vehicle Bus[J]. IEEE Transactions on Vehicular Technology, 2007, 56(6): 3695-3708.

[5]朱琴跃, 谢维达, 谭喜堂,等. MVB周期信息的实时调度[J]. 计算机应用, 2007, 27(12): 3108-3111, 3115.

(ZHU Qinyue, XIE Weida, TAN Xitang, et al. Real-Time Scheduling of Periodic Messages for MVB[J]. Computer Application, 2007, 27(12): 3108-3111, 3115. in Chinese)

[6]聂晓波. 列车控制网络实时性能分析及调度策略研究[D]. 北京: 北京交通大学, 2011.

(NIE Xiaobo. Analysis and Real-Time Scheduling Policy Research Performance Train Control Network[D]. Beijing: Beijing Jiaotong University, 2011. in Chinese)

[7]王永翔, 王立德. 多功能车辆总线周期扫描表的最优化设计[J]. 铁道学报, 2009, 31(6): 46-52.

(WANG Yongxiang, WANG Lide. The Optimization Method of the MVB Period Polling Table[J]. Journal of the China Railway Society, 2009, 31(6): 46-52. in Chinese)

[8]陈佳凯, 韦巍. 基于多目标粒子群优化的多功能车辆总线周期性扫描表的优化[J]. 铁道学报, 2012, 34(11): 60-66.

(CHEN Jiakai, WEI Wei. Optimization of the MVB Period Polling Table Based on Multi-Objective Particle Swarm Optimization[J]. Journal of the China Railway Society, 2012, 34(11): 60-66. in Chinese)

[9]李锐, 李永宗, 费巧玲，等. 一种多功能车辆总线周期扫描表优化设计方案[J]. 机车电传动, 2013 (4): 92-94.

(LI Rui, LI Yongzong, FEI Qiaoling, et al. An Optimization Solution of the MVB Periodic Polling Table[J]. Electric Drive for Locomotives, 2013 (4): 92-94. in Chinese)

[10]郭超勇, 刘建强, 郑琼林，等. 350 km/h动车组TCN网络周期轮询优化算法研究[J]. 铁道学报, 2011, 33(12): 46-50.

(GUO Chaoyong, LIU Jianqiang, ZHENG Qionglin, et al. Research on the TCN Network Periodic Polling Optimization Algorithm for the 350 km/h Electrical Multiple Units[J]. Journal of the China Railway Society, 2011, 33(12): 46-50. in Chinese)

[11]王涛, 王立德, 周洁琼，等. MVB网络周期轮询算法优化与仿真研究[J]. 机车电传动, 2013 (6): 40-45.

(WANG Tao, WANG Lide, ZHOU Jieqiong, et al. Cycle Polling Algorithm Optimization and Simulation Research of MVB Network[J]. Electric Drive for Locomotives, 2013 (6): 40-45. in Chinese)

[12]WHITLEY D. A Genetic Algorithm Tutorial[J]. Statistics and Computing， 1994, 4(2): 65-85.

[13]DEB K, PRATAP A, AGARWAL S, et al. A Fast and Elitist Multiobjective Genetic Algorithm: NSGA-II[J]. IEEE Transactions on Evolutionary Computation, 2002, 6(2): 182-197.

[14]PETEGHEMA V V, VANHOUCKEA M. A Genetic Algorithm for the Preemptive and Non-Preemptive Multi-Mode Resource-Constrained Project Scheduling Problem[J]. European Journal of Operational Research, 2010, 201(2): 409-418.

[15]CHUN J S, KIM M K, JUNG H K, et al. Shape Optimization of Electromagnetic Devices Using Immune Algorithm[J]. IEEE Transactions on Magnetics, 1997, 33(2): 1876-1879.