钢桥腐蚀斜焊缝十字接头疲劳性能研究

揭志羽，李亚东，卫　星，诸葛萍

(1.宁波大学 建筑工程与环境学院， 浙江 宁波　315211；2.西南交通大学 土木工程学院，四川 成都　610031)

疲劳和腐蚀是引起钢桥性能退化的重要原因[1-2]。钢桥焊接接头在交通荷载产生的交变应力下容易产生微裂纹，并不断扩展为宏观裂纹，最终导致疲劳破坏。国内外学者基于名义应力法和热点应力法对焊接接头疲劳问题进行了大量的研究[3-10]。焊接接头长期暴露在温度、湿度较高并常含有各种污染物的自然环境中，容易发生腐蚀，在表面产生腐蚀坑等损伤，导致应力集中，同时还缩小截面面积，从而加速焊接接头的疲劳断裂。Rahgozar和Rahgozar[11]从3个腐蚀钢梁的腹板和翼缘获得76个标准试件，采用液压伺服疲劳试验机对每个试件进行疲劳试验，通过腐蚀坑深度建立了点蚀与剩余疲劳寿命的定量关系。Garbatov等[12]分析小规模腐蚀钢焊接试件的疲劳强度，结果表明腐蚀导致试件的疲劳强度降低；非腐蚀试件的疲劳失效是沿着焊趾，而腐蚀试件的疲劳失效均起源于腐蚀坑处。Huang等[13]对腐蚀和疲劳共同作用下焊接结构的疲劳进行评估。

美国船级社给出了不同焊接接头在海水自由腐蚀中的S—N曲线表达式，但是并没有明确海水自由腐蚀时间以及相应的腐蚀程度，而不同腐蚀时间下的疲劳强度是有差别的[14]。

实际钢桥中存在大量的倾斜焊接接头，并容易受到环境腐蚀的影响，因此本文根据国内外文献，以不同腐蚀程度的45°倾角全熔透承载角焊缝十字接头为研究对象，通过预腐蚀试验构造2种不同深度的人工半球形蚀坑。采用疲劳试验和有限元分析方法对腐蚀的斜焊缝十字接头的疲劳行为进行研究。

1　斜焊缝十字接头预腐蚀试验

在海洋大气环境中，钢桥会出现大量点蚀，产生的应力集中对钢桥疲劳寿命的影响比均匀腐蚀严重得多。一般采用腐蚀深度评定点蚀损伤。根据国内外文献，蚀坑深度与时间存在幂函数关系，即

d=Atn

(1)

式中：d为腐蚀深度，mm；t为时间，a；A和n为参数。

根据文献[15]中给出的海洋大气环境下蚀坑深度的平均值确定幂函数中的相关参数为A=0.062 mm，n=0.862，则式(1)可以写为

d=0.062t0.862

(2)

因此，根据式(2)可以得到海洋大气环境下蚀坑深度与时间的定量关系。

为了研究人工蚀坑对斜焊缝十字接头疲劳寿命的影响，根据实际腐蚀情况采用机械加工方法近似构造2种不同深度的人工半球形蚀坑，蚀坑尺寸参数见表1。每个试件都在边缘焊趾附近加工8个相同的人工蚀坑，厚度方向对称分布，试件尺寸以及蚀坑分布分别如图1和图2所示。

表1　蚀坑尺寸参数

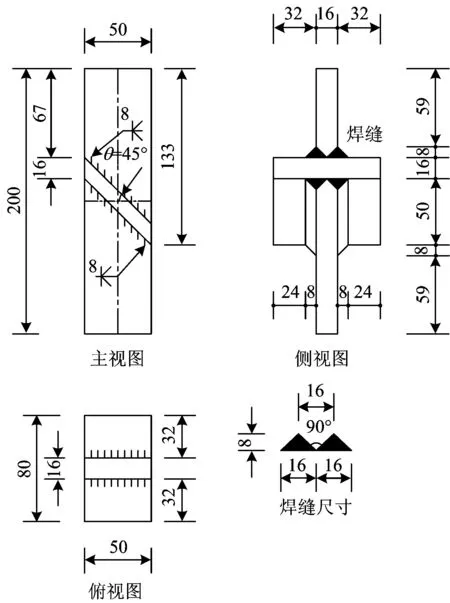
图1　斜焊缝十字接头尺寸(单位：mm)

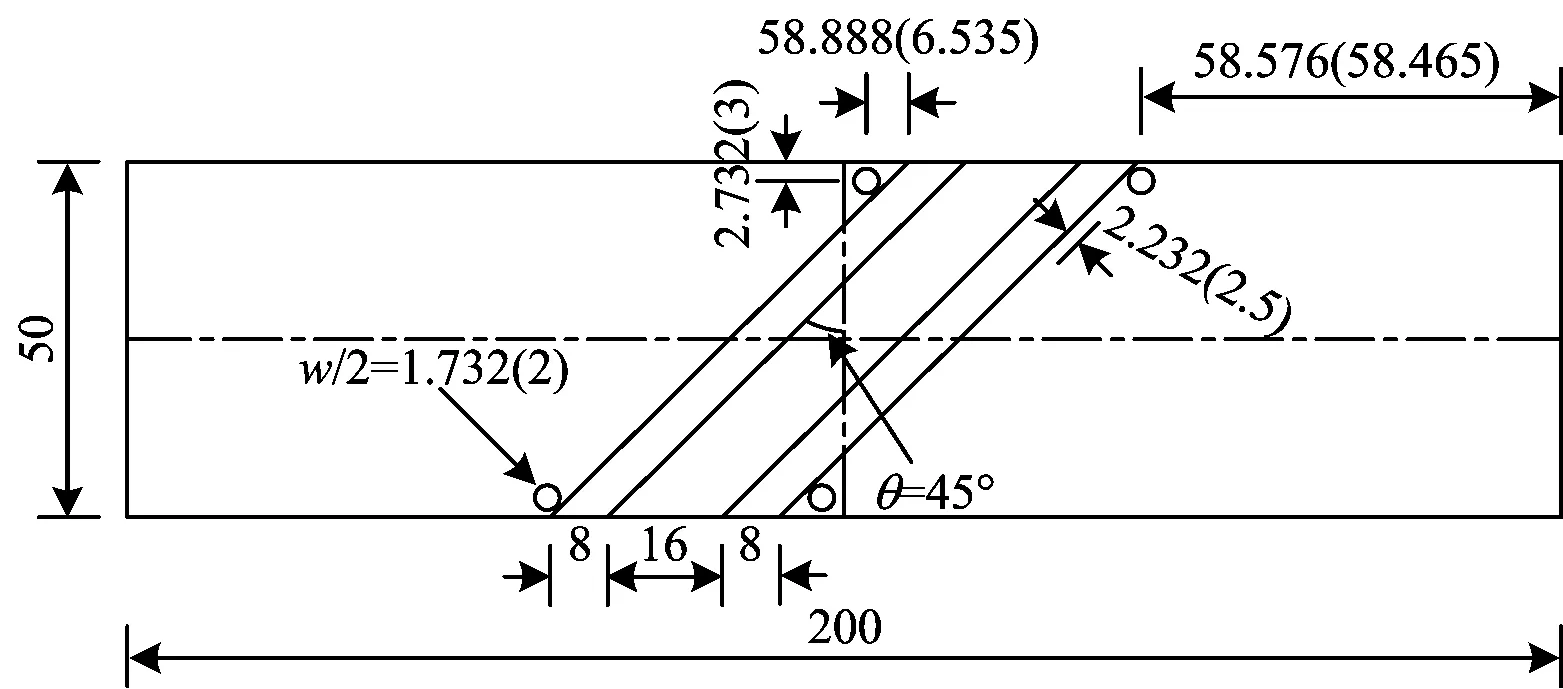
图2　蚀坑分布(单位：mm)

2　斜焊缝十字接头疲劳试验

2.1　试验方法及结果

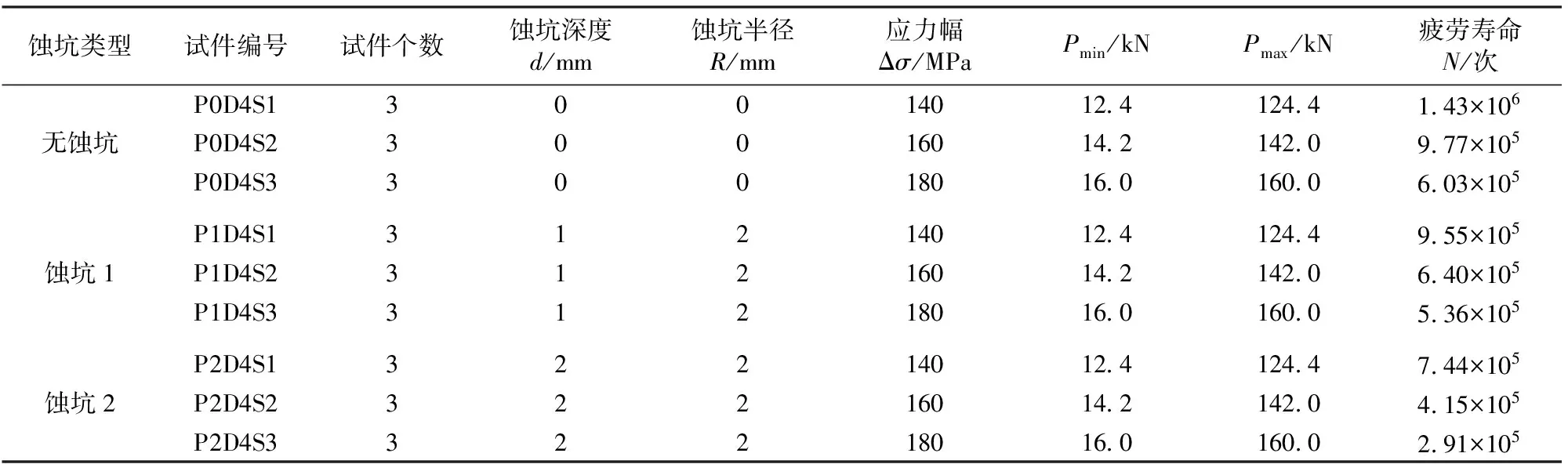
分别对无蚀坑、含蚀坑1和含蚀坑2的45°倾角全熔透承载角焊缝十字接头试件进行轴向拉伸疲劳试验。采用正弦波加载，荷载应力比均为0.1，加载频率为5～10 Hz之间，根据实际加载条件以及疲劳极限，在端部分别施加140，160和180 MPa的应力幅，疲劳加载的最大值和最小值分别用Pmax和Pmin表示。由于焊接接头疲劳试验结果的离散性较大，因此每个应力幅均采用3个试件，总共27个试件。疲劳试件底部通过连接板固定在锚固梁上，顶部通过连接板与作动器连接，含人工蚀坑斜焊缝十字接头疲劳加载如图3所示。试验中将疲劳裂纹沿厚度贯穿时所对应的循环加载次数作为试件的疲劳寿命，不同腐蚀深度下斜焊缝十字接头疲劳寿命试验结果见表2。

图3　十字接头疲劳加载

大部分斜焊缝十字接头试件是在焊缝方向与纵向夹角为钝角的边缘焊趾处开裂，如图4所示。产生这种现象的主要原因是：焊趾处存在应力集中，同时蚀坑的存在改变了焊趾附近应力应变场的分布，两者的叠加作用最终导致焊趾处裂纹扩展方向发生变化，不再沿着平面扩展，而是形成了有一定偏转角的裂纹。

图4　斜焊缝十字接头裂纹扩展

蚀坑类型试件编号试件个数蚀坑深度d/mm蚀坑半径R/mm应力幅Δσ/MPaPmin/kNPmax/kN疲劳寿命N/次P0D4S130014012 4124 41 43×106无蚀坑P0D4S230016014 2142 09 77×105P0D4S330018016 0160 06 03×105P1D4S131214012 4124 49 55×105蚀坑1P1D4S231216014 2142 06 40×105P1D4S331218016 0160 05 36×105P2D4S132214012 4124 47 44×105蚀坑2P2D4S232216014 2142 04 15×105P2D4S332218016 0160 02 91×105

图5为斜焊缝十字接头的疲劳断口，从图5可以看出，在右下角处形成疲劳裂纹源，裂纹不断扩展形成光滑区域，并且穿过蚀坑，从疲劳断面能观察到疲劳裂纹扩展的轨迹线，最终疲劳断裂形成粗糙区。

图5　斜焊缝十字接头的疲劳断口

2.2　结果分析

根据表2中的疲劳寿命试验结果，运用最小二乘法进行无蚀坑、含蚀坑1和含蚀坑2斜焊缝十字接头的应力幅与疲劳寿命拟合。由于规范上大多数S—N曲线采用的斜率为m=3，因此本文也将斜率m取为3，得到无蚀坑、含蚀坑1和含蚀坑2的45°倾角全熔透承载角焊缝十字接头S—N曲线(保证率50%)的拟合表达式分别为

lgN=12.574-3lgΔσ

(3)

lgN=12.438-3lgΔσ

(4)

lgN=12.252-3lgΔσ

(5)

将式(3)—式(5)减去2倍lgN的标准差(0.376,0.256，和0.412)，可得到保证率为97.7%时的相应S—N曲线表达式

lgN=12.198-3lgΔσ

(6)

lgN=12.182-3lgΔσ

(7)

lgN=11.840-3lgΔσ

(8)

Eurocode3[16]中给出了0°倾角的全熔透承载角焊缝十字接头S—N曲线(保证率97.7%)表达式

lgN=11.855-3lgΔσ

(9)

运用式(6)—式(9)计算保证率为97.7%、倾角为0°以及无蚀坑、含蚀坑1和含蚀坑2的45°倾角十字接头在200万次循环加载下的疲劳强度，结果见表3。

表3　不同蚀坑类型疲劳强度

由表3可以得到以下结论。

(1)在保证率为97.7%的条件下，0°倾角和45°倾角无蚀坑十字接头在200万次循环次加载后的疲劳强度分别为71.0和92.4 MPa，45°倾角时增大了30.1%，这说明随着倾角的增大，疲劳强度增大。

(2)在保证率为97.7%的条件下，含蚀坑1和含蚀坑2的十字接头在200万次循环加载下的疲劳强度分别为91.3和70.2 MPa，比无蚀坑时分别下降了1.2%和24%，当0≤d≤1 mm时，疲劳强度基本没有变化，当1 mm≤d≤2 mm时，疲劳强度降低明显。0°倾角与含蚀坑2的45°倾角十字接头的S—N曲线非常接近，说明两者疲劳强度大致相当。

(3)斜焊缝十字接头在不同腐蚀程度下的疲劳寿命不同，因此不能采用相同的S—N曲线考虑不同腐蚀程度的影响。

本文给出的式(6)—式(8)可为不同腐蚀程度斜焊缝十字接头的抗疲劳设计提供帮助。

3　蚀坑对斜焊缝十字接头应力集中的影响

基于有限元方法从应力集中角度分析蚀坑导致斜焊缝十字接头疲劳强度下降的原因，对不同腐蚀程度斜焊缝十字接头的应力场分布规律进行分析，并建立热点应力集中系数模型。

3.1　应力集中数值模拟

为了研究蚀坑对斜焊缝十字接头应力场分布的影响规律，利用大型通用有限元软件ANSYS建立含不同蚀坑的斜焊缝十字接头有限元模型。采用10节点四面体实体单元SOLID92进行网格划分，如图6所示。Q345qC钢的材料参数：泊松比ν=0.3，弹性模量E=2.1×105MPa。荷载和边界条件：一端固定，一端施加160 MPa的面荷载。分析中选取表4所示的5种不同尺寸的蚀坑。

表4　5种不同尺寸的蚀坑

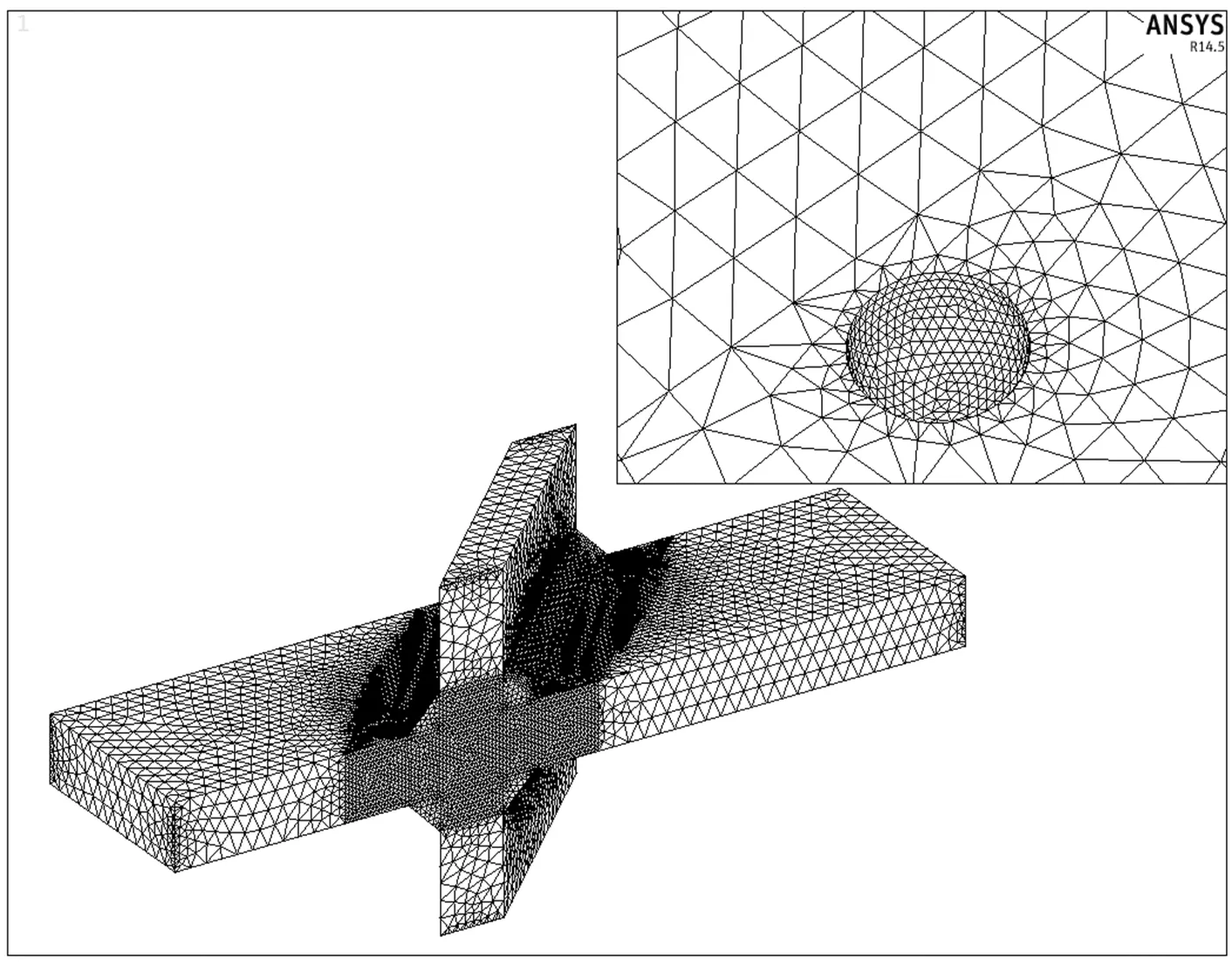
图6　含蚀坑的斜焊缝十字接头有限元模型

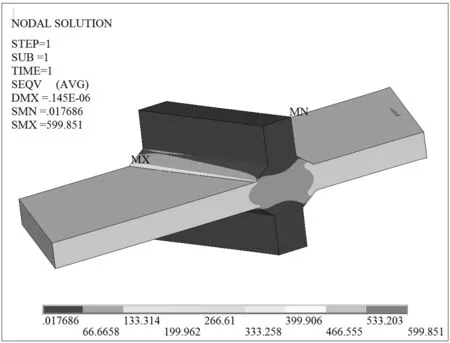
图7含蚀坑P0的斜焊缝十字接头Von Mises等效应力(单位：MPa)

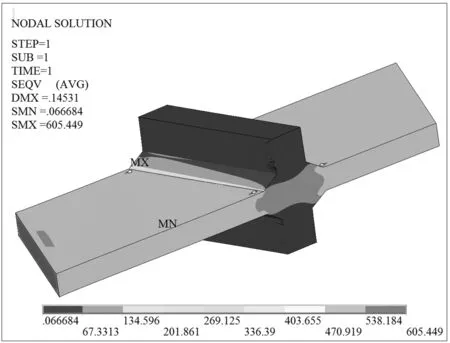
图8含蚀坑P1的斜焊缝十字接头Von Mises等效应力(单位：MPa)

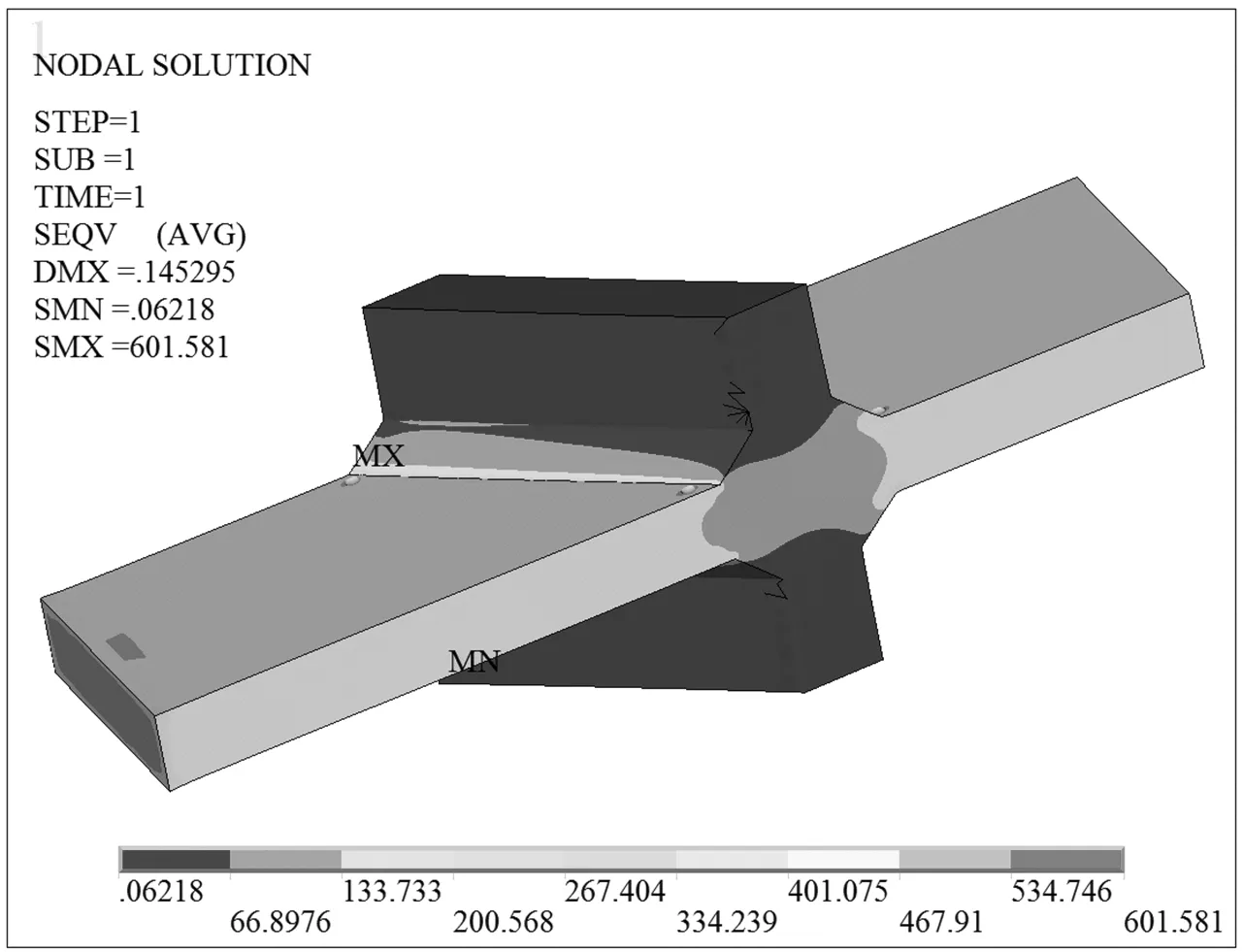
图9含蚀坑P2的斜焊缝十字接头Von Mises等效应力(单位：MPa)

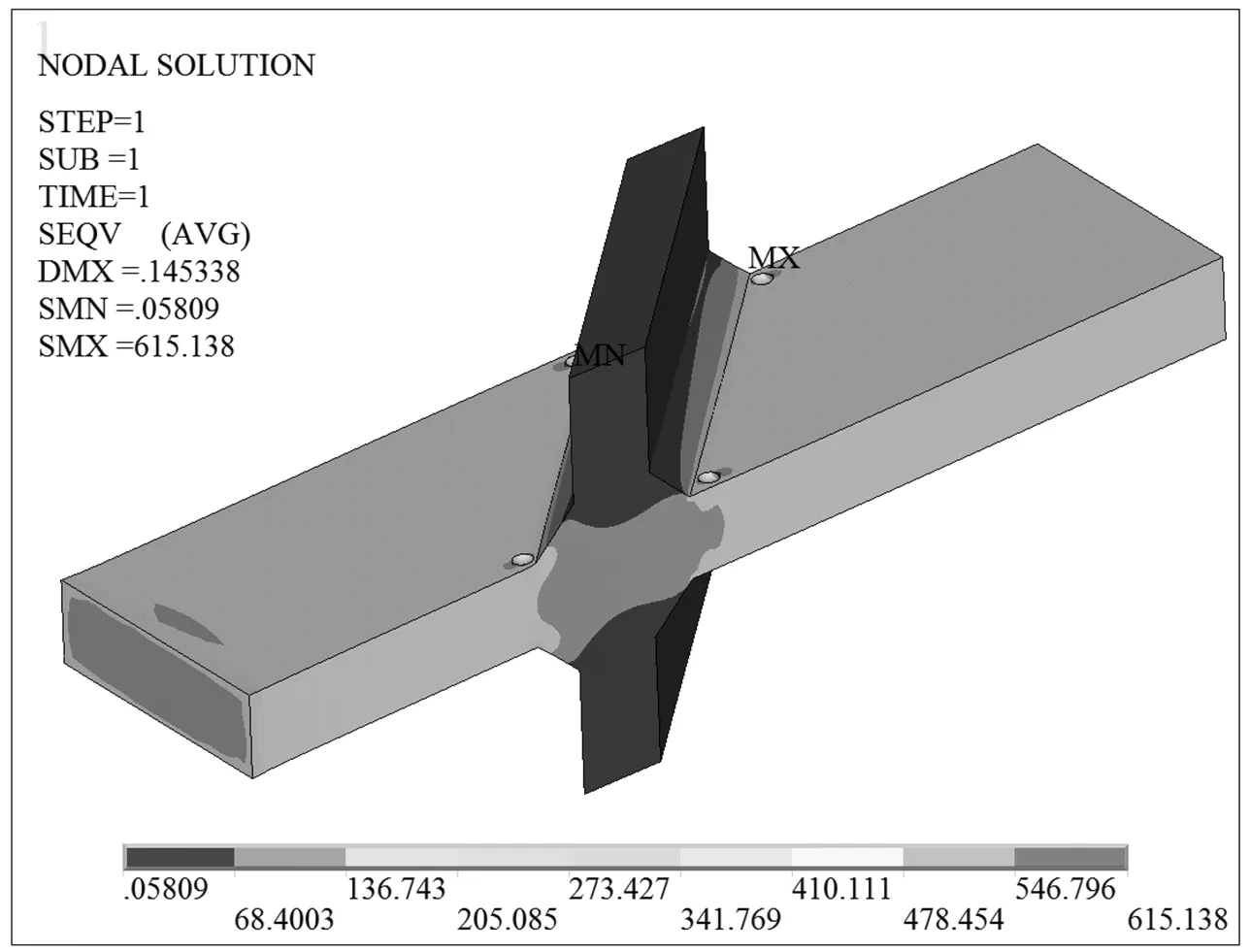
图10含蚀坑P3的斜焊缝十字接头Von Mises等效应力(单位：MPa)

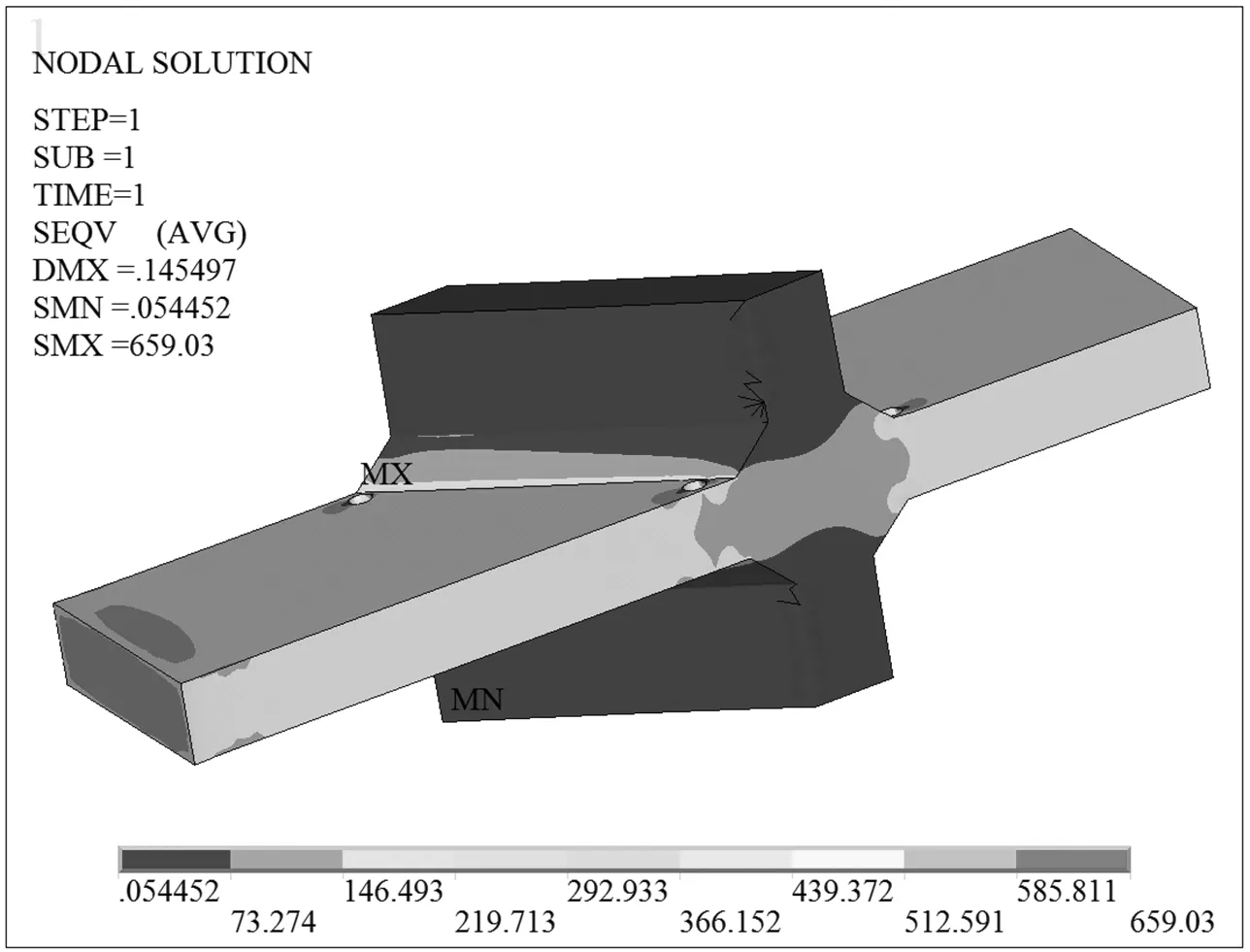
图11含蚀坑P4的斜焊缝十字接头Von Mises等效应力(单位：MPa)

含5种不同尺寸蚀坑的斜焊缝十字接头Von Mises等效应力如图7—图11所示。从图中可以看出：①在蚀坑半径相同情况下，等效应力随着蚀坑深度的增大而增大，且都在焊缝方向与纵向夹角为钝角的边缘焊趾处达到最大值，试验结果也验证了该处是疲劳裂纹源；②当0≤d≤1 mm时，等效应力增大很小，当1 mm≤d≤2 mm时，等效应力增大明显；③在蚀坑深度都为1 mm的情况下，蚀坑宽度由2 mm增大为3.464 mm时，等效应力从605 MPa变为615 MPa，增大幅度仅为1.7%，所以说蚀坑宽度对应力集中的影响很小；④蚀坑P0，P3和P4分别对应于无蚀坑、含蚀坑1和含蚀坑2，它们的等效应力最大值分别为600，615和659 MPa。

3.2　热点应力集中系数

为了定量分析不同腐蚀程度下斜焊缝十字接头应力集中程度的大小，采用弹性应力集中系数作为衡量标准，而应力集中数值模拟结果与网格划分有很大的关系，为了避免网格划分带来的误差，采用热点应力分析应力场的变化规律。将弹性热点应力集中系数定义为

(10)

式中：σhs为热点应力；σnom为端部名义应力。

通过距焊趾0.4T和1.0T处(T为主板厚度)的Von Mises等效应力线性外推热点应力。

根据3.1节中可以知道，在相同蚀坑深度下可以不考虑蚀坑宽度对应力集中的影响，因此基于有限元模型计算不同蚀坑(蚀坑半径为2 mm)的热点应力，进而根据式(10)得到相应的热点应力集中系数，见表5。

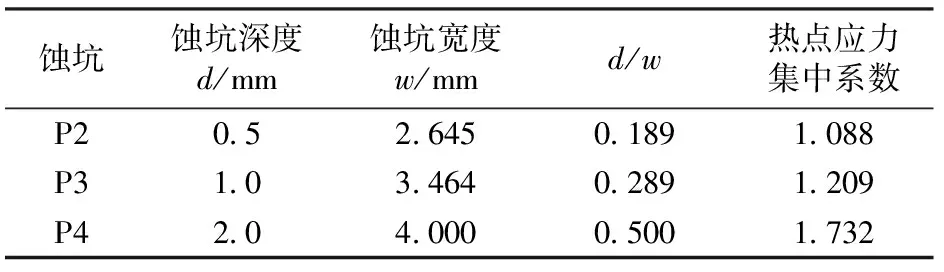
表5　不同蚀坑尺寸下斜焊缝十字接头热点应力集中系数

为了确定热点应力集中系数Kt与蚀坑深度d、深宽比d/w之间的相关性，分别采用线性和非线性2种函数拟合它们的关系，线性函数表达式为

Kt=α+βd

(11)

(12)

式中：α和β为拟合系数。

非线性函数表达式为[17]

(13)

(14)

式中：η和λ为拟合系数。

分别基于线性函数和非线性函数拟合热点应力集中系数与蚀坑深度、深宽比的关系，如图12—图15所示。

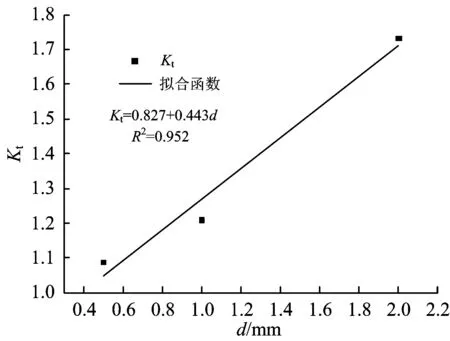
图12基于线性函数的热点应力集中系数与蚀坑深度的关系

图13基于线性函数的热点应力集中系数与蚀坑深宽比的关系

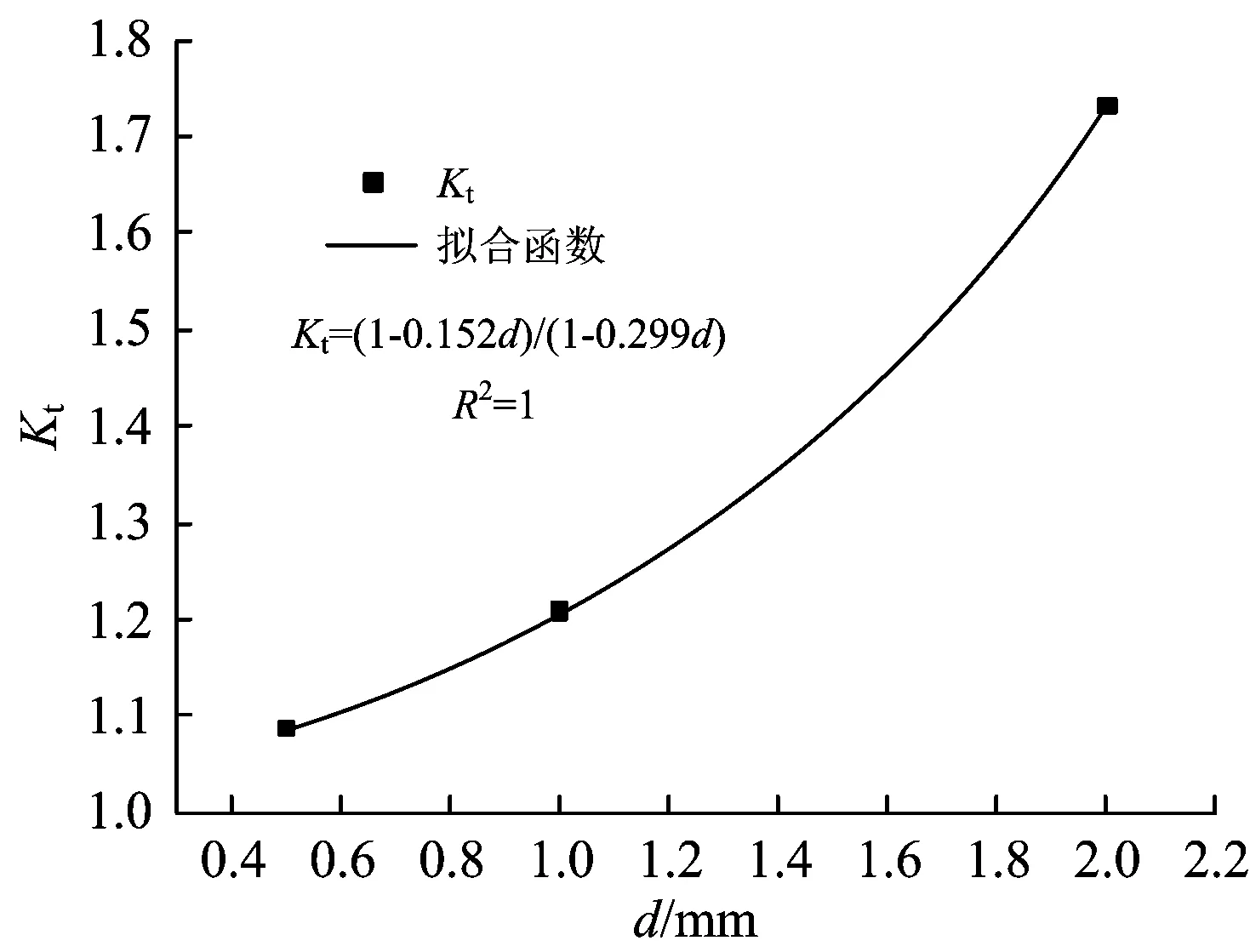
图14基于非线性函数的热点应力集中系数与蚀坑深度的关系

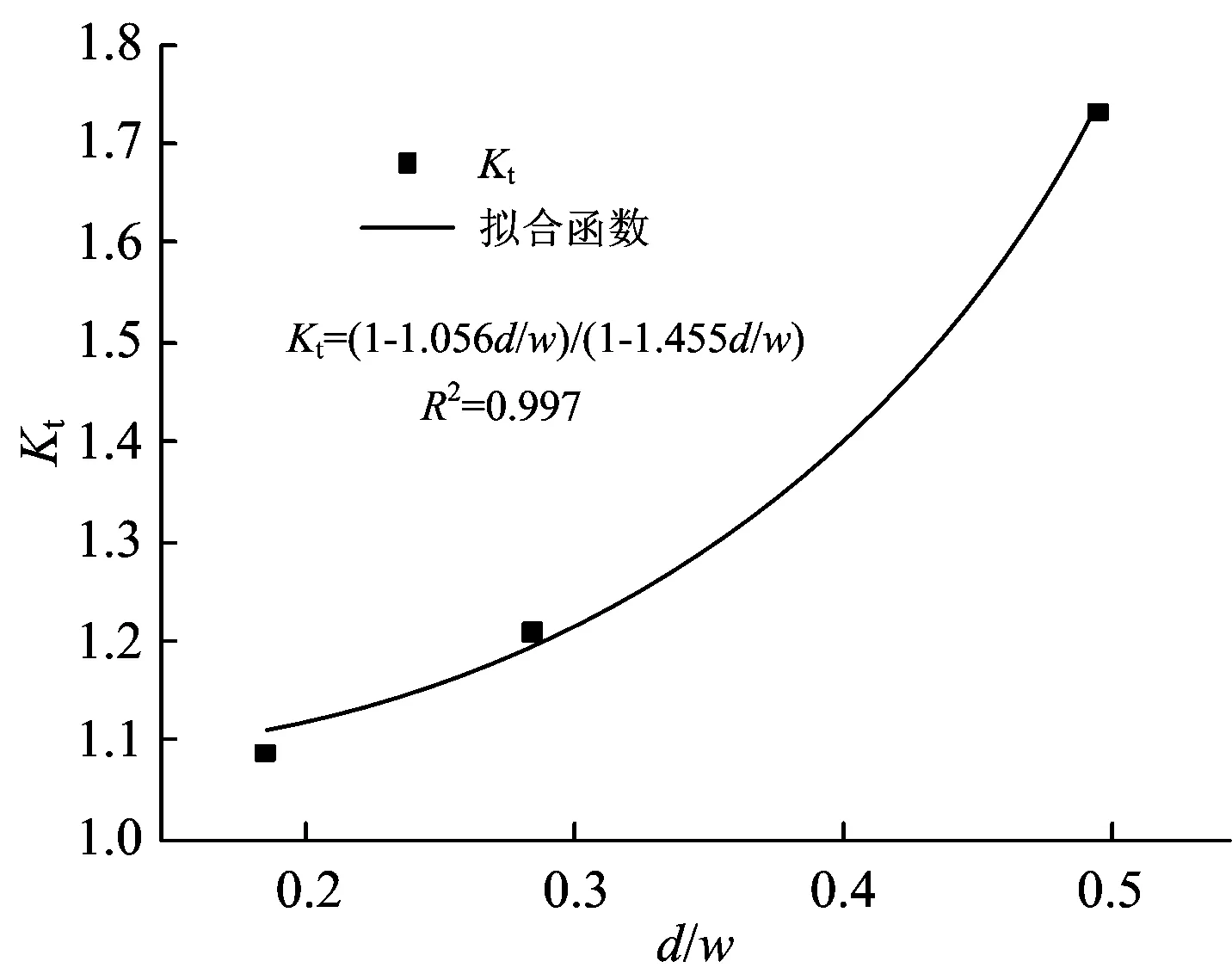
图15基于非线性函数的热点应力集中系数与蚀坑深宽比的关系

从表5和图12—图15可以得出以下结论。

(1)随着蚀坑深度和深宽比的增大，热点应力集中系数增大，并且增长速率越来越大，当蚀坑深度d从0增大到1 mm时，热点应力集中系数增大了11.6%，当蚀坑深度d从1 mm增大到2 mm时，热点应力集中系数增大了43.3%。

(2)基于非线性函数的热点应力集中系数与蚀坑深度和深宽比的相关性比线性函数的好，而在非线性函数中热点应力集中系数与蚀坑深度的相关性要优于蚀坑深宽比，因此推荐采用非线性函数拟合热点应力集中系数与蚀坑深度的关系，其表达式为

(15)

4　结　论

(1)无蚀坑、含蚀坑1和含蚀坑2斜焊缝十字接头在200万次循环加载下的疲劳强度分别为92.4，91.3，和70.2 MPa，当d≤1 mm时，可以忽略蚀坑对疲劳强度的影响，斜焊缝十字接头S—N曲线应该考虑不同腐蚀程度的影响。

(2)在蚀坑半径相同情况下，蚀坑越深，等效应力越大，应力集中越明显；在蚀坑深度相同情况下，随蚀坑宽度增大，等效应力几乎不变。所以说蚀坑宽度对应力集中的影响很小，蚀坑深度是影响斜焊缝十字接头疲劳强度的主要因素。

(3)随着蚀坑深度和深宽比的增大，热点应力集中系数增大，并且增长速率越来越大。由于热点应力集中系数与蚀坑深度的相关性要好于深宽比，且非线性函数优于线性函数，因此推荐采用非线性函数拟合热点应力集中系数与蚀坑深度的关系。

[1]COCA F, TELLO M, GAONA-TIBURCIO C, et al. Corrosion Fatigue of Road Bridges: a Review[J]. Interna-tional Journal of Electrochemical Science, 2011,6(8):3438-3451.

[2]任必年. 公路钢桥腐蚀与防护[M]. 北京: 人民交通出版社, 2002.

(REN Binian. Corrosion and Protection of Highway Steel Bridge[M]. Beijing: China Communications Press, 2002.in Chinese)

[5]LOTSBERG I. Fatigue Design of Welded Pipe Penetrations in Plated Structures[J]. Marine Structures, 2004,17(1):29-51.

[6]LOTSBERG I. Fatigue Design Criteria as Function of the Principal Stress Direction Relative to the Weld Toe[C]//American Society of Mechanical Engineers. Proceedings of the ASME 27th International Conference on Offshore Mechanics and Arctic Engineering, New York:American Society of Mechanical Engineers，2008.

[7]LOTSBERG I. Assessment of Design Criteria for Fatigue Cracking from Weld Toes Subjected to Proportional Loading[J]. Ships and Offshore Structures, 2009,4(2):175-187.

[8]武奇. 基于结构应力的焊接接头疲劳分析及多轴高周疲劳寿命估算[D]. 上海: 同济大学, 2009.

(WU Qi. Fatigue Analysis and Multiaxial High-Cycle Fatigue Life Prediction of Welded Joints Based on Structural Stress[D]. Shanghai: Tongji University, 2009.in Chinese)

[9]周张义, 李芾, 安琪, 等. 钢结构焊缝疲劳强度分析技术的最新进展[J]. 中国铁道科学, 2009,30(4):69-75.

(ZHOU Zhangyi，LI Fu，AN Qi, et al. Latest Development of Fatigue Strength Analysis Technology for Welds in Steel Structures [J]. China Railway Science, 2009,30(4):69-75.in Chinese)

[10]赵欣欣, 刘晓光, 潘永杰, 等. 正交异性钢桥面板纵肋腹板与面板连接构造的疲劳试验研究[J]. 中国铁道科学, 2013,34(2):41-45.

(ZHAO Xinxin，LIU Xiaoguang，PAN Yongjie, et al. Fatigue Test Study on the Joint Structure between the Deck and Longitudinal Rib Web of Orthotropic Steel Bridge Deck[J]. China Railway Science, 2013,34(2):41-45.in Chinese)

[11]RAHGOZAR R, SHARIFI Y. Remaining Fatigue Life of Corroded Steel Structural Members[J]. Advances in Structural Engineering, 2011,14(5):881-890.

[12]GARBATOV Y, SOARES C G, PARUNOV J. Fatigue Strength Experiments of Corroded Small Scale Steel Specimens[J]. International Journal of Fatigue, 2014,59:137-144.

[13]HUANG W, GARBATOV Y, GUEDES SOARES C. Fatigue Reliability of a Web Frame Subjected to Random Non-Uniform Corrosion Wastage[J]. Structural Safety, 2014,48:51-62.

[14]American Bureau of Shipping. Guide for the Fatigue Assessment of Offshore Structures[S]. Houston:American Bureau of Shipping, 2003.

[15]曹楚南. 中国材料的自然环境腐蚀[M]. 北京: 化学工业出版社, 2005.

(CAO Chunan. Corrosion in Natural Environment of Materials in China[M]. Beijing:Chemical Industry Press, 2005.in Chinese)

[16]European Committee for Standardization.EN 1993-1-9 Eurocode 3: Design of Steel Structures Part 1-9: Fatigue[S]. Brussels:European Committee for Standardization, 2005.

[17]秦广冲, 徐善华, 何羽玲, 等. 初、次级蚀坑三维变化对钢板应力集中系数的影响[J]. 材料科学与工程学报, 2015,33(2):251-256.

(QIN Guangchong, XU Shanhua, HE Yuling, et al. Effect of Dimensional Variations of Primary and Secondary Pits on Stress Concentration Factor[J]. Journal of Material Science & Engineering, 2015,33(2):251-256.in Chinese)