一类5阶常微分方程特征值的上界

吴 平

(苏州市职业大学 数理部，江苏 苏州 215104)

一类5阶常微分方程特征值的上界

吴 平

(苏州市职业大学 数理部，江苏 苏州 215104)

根据Rayleigh定理、分部积分及不等式估计等方法，得到一类5阶常微分方程特征值估计的上界的不等式，其估计系数与区间的几何度量无关。其结果在物理学和力学等领域有着广泛的应用。

一类5阶常微分方程；特征值；上界；估计

1 问题的提出

其中u1，u2为正实数。

由分部积分法，可得

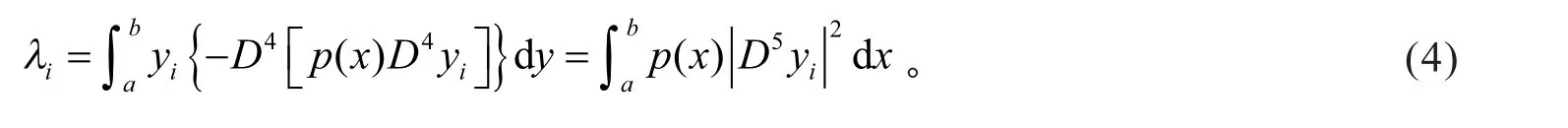
由式 (2)及式(4)，可得

假设。显然，aij=aji，φi与yj正交(i，j=1，2，…，n)。

由Rayleigh定理，可得不等式

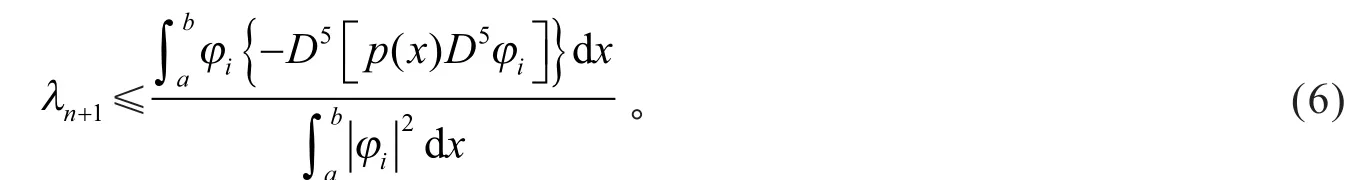
计算得

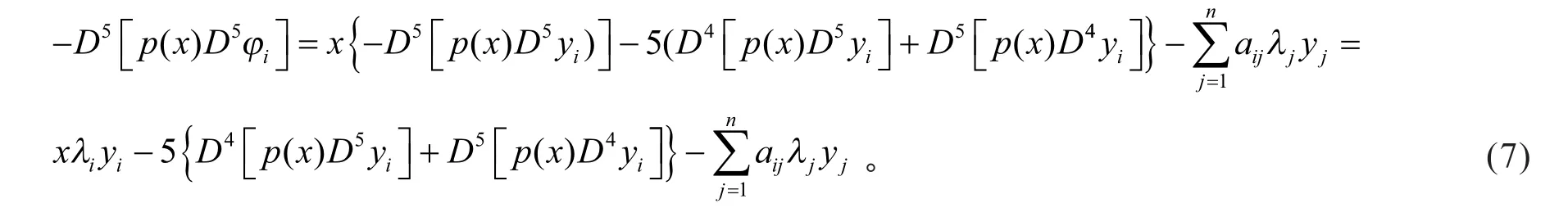
根据φi和yj的正交性及，由式(7)，可得

假设

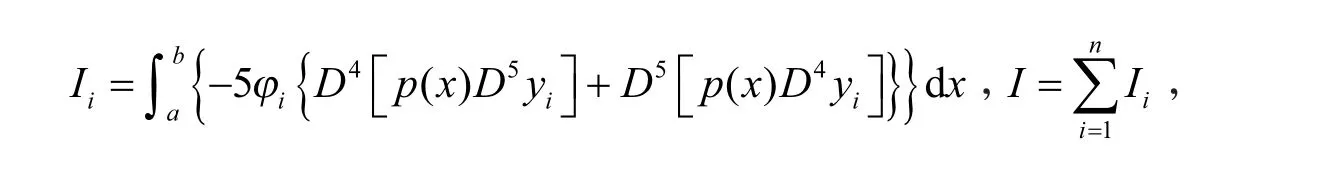
由式(8)，可得

由式(6)、式(9)，可得

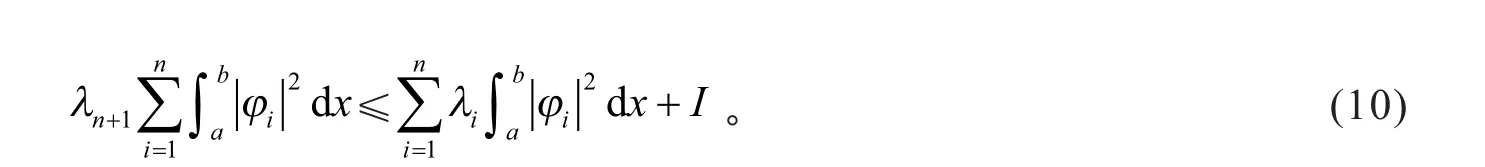
用λn代替式(10)中的λi，可得

2 引理

引理1 设yi是问题(1)对应特征值λi的特征函数，则

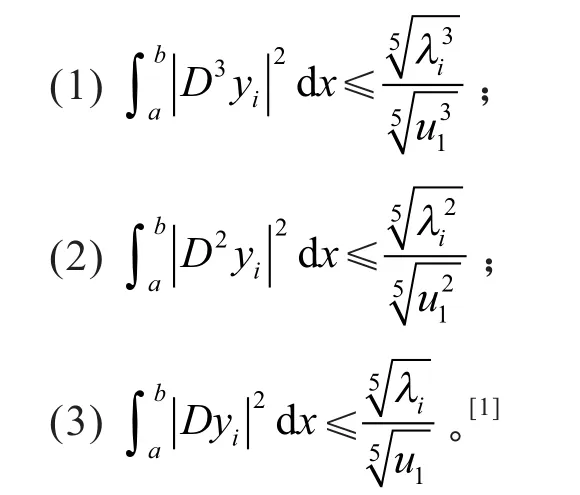
证明 由分部积分、Schwartz不等式，可得

同理

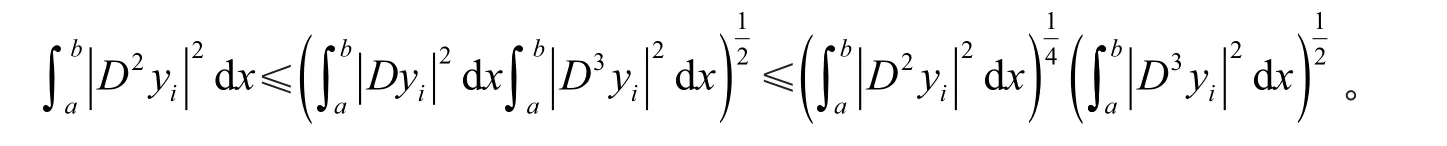
化简，可得

由分部积分、Schwartz不等式、式(12)、式(13)及式(5)，有

化简可得引理1(1)。引理1(1)代入式(13)可得引理1(2)。引理1(1)、引理1(2)代入式(12)即得引理1(3)。

引理2 设y1，y2，…，yn为问题(1)的n个特征值，则

证明

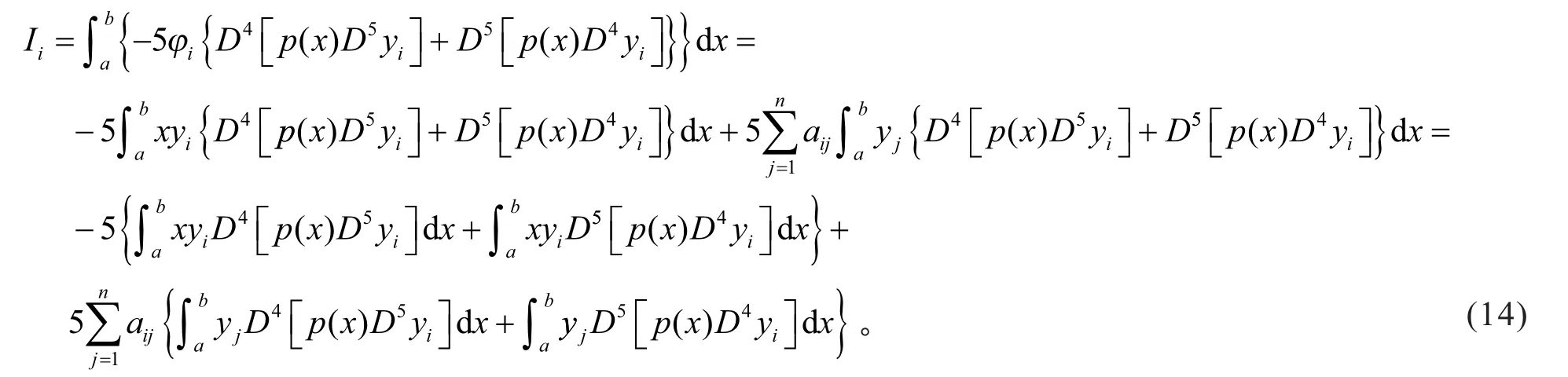
由分部积分，可得

由式(14)、式(15)、式(16)及式(17)，可得

根据式(18)，得

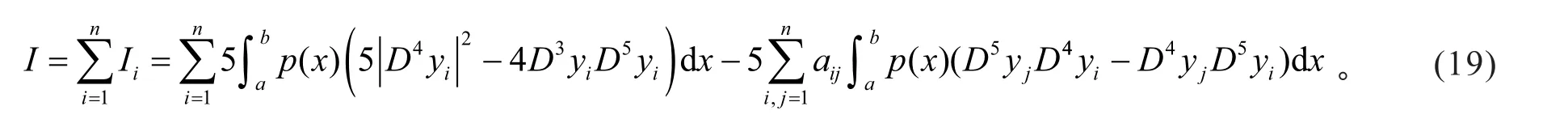
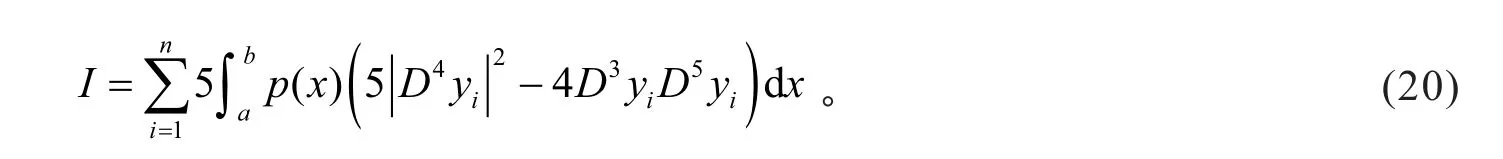
根据式(2)、引理1(1)及式(5)，有

根据式(2)、Schwartz不等式、引理1(1)及式(5)，有

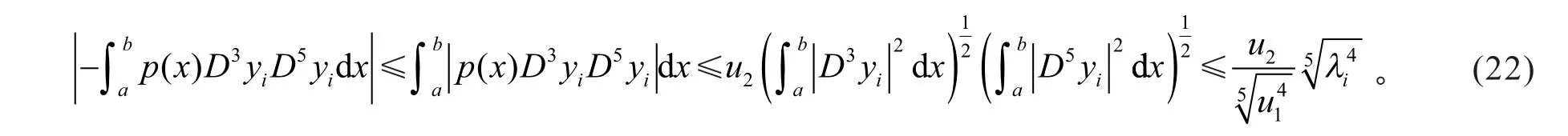
根据式(20)、式(21)及式(22)，有

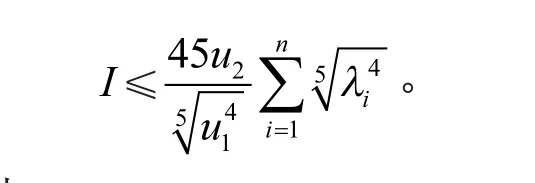
引理3 对于φi和λi(i=1，2，…，n)，则

证明 由φi的定义，得

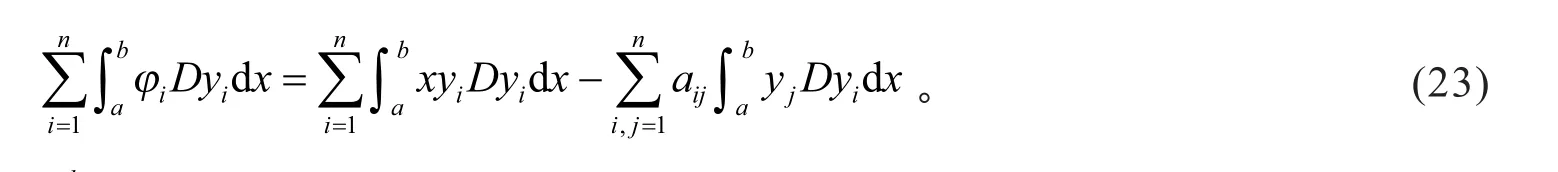
由分部积分，可得

即有

可得

根据式 (24)、式(25)，有

由Schwartz不等式、引理1(3)，可得

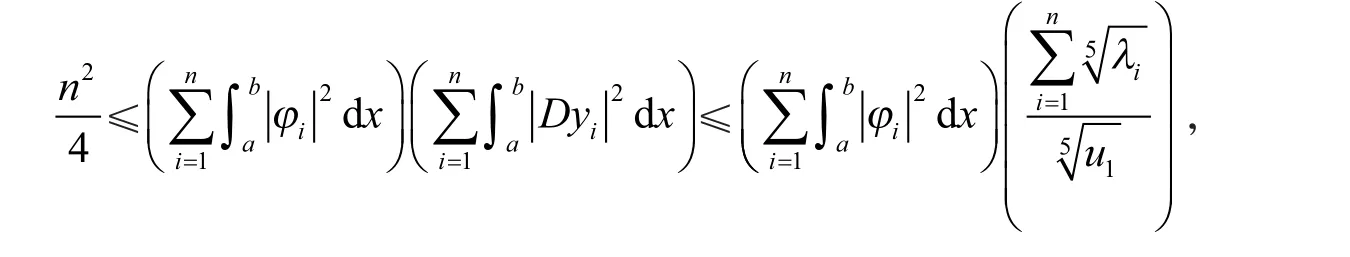
化简即得引理3。

3 结论

定理1 如果λi(i=1，2，…，n+1)是问题(1)的特征值，则

证明 根据引理3，有

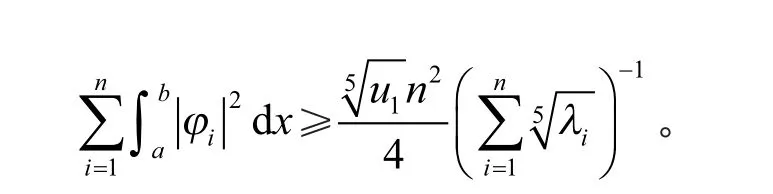
再由式(11)及引理2，可得定理1(1)。在定理1(1)中右端用λn代替λi可得定理1(2)。

定理2 对于n≥1，则

证明 选参数σ＞λn，由式(10)，有

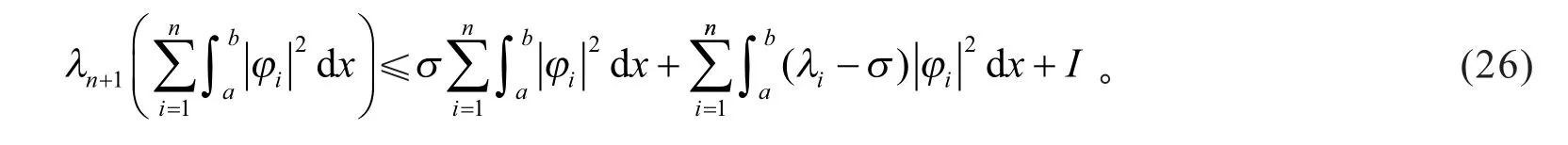
根据及Young不等式，可得

式中δ＞0，是待定系数。

根据式(26)、式(27)及引理1(2)，可得

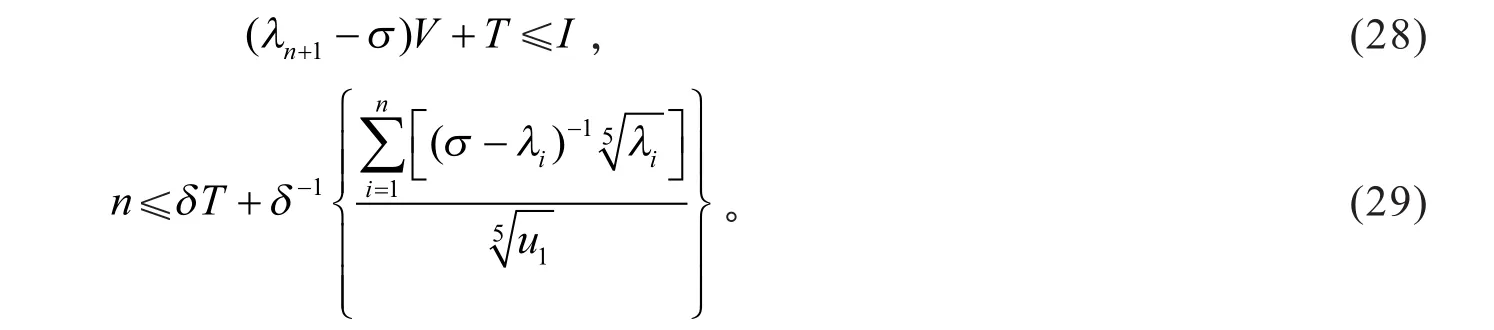
为使式(29)右端的值达到最小，取

将式(30)代入式(29)，可得

由引理2、式(28)、式(31)，可得

Upper Bound for Eigenvalues for a Five-order Differential Equation

WU Ping
(Department of Mathematics and Physics，Suzhou Vocational University，Suzhou 215104，China)

This paper considers the estimates for eigenvalues of a differential equation. Some test function is constructed and then the Rayleigh theorem is used to obtain a basic inequality.

a differential equation ；eigenvalue；upperbound；estimates

O175.9

A

1008-5475(2017)01-0036-05

10.16219/j.cnki.szxbzk.2017.01.008

2016-11-24；

2016-12-20

吴 平(1962-)，男，江苏苏州人，副教授，主要从事方程的特征值研究。

吴平.一类5阶常微分方程特征值的上界[J].苏州市职业大学学报，2017，28(1)：36-40，63.