椭球壳液压胀形过程焊缝建模方式的研究
张伟玮,滕步刚,2
(1 哈尔滨工业大学 材料科学与工程学院,哈尔滨 150001; 2 哈尔滨工业大学 金属精密热加工国家重点实验室,哈尔滨 150001)
椭球壳液压胀形过程焊缝建模方式的研究
张伟玮1,滕步刚1,2
(1 哈尔滨工业大学 材料科学与工程学院,哈尔滨 150001; 2 哈尔滨工业大学 金属精密热加工国家重点实验室,哈尔滨 150001)
为了研究焊缝区域有限元建模方式对椭球壳胀形过程轴长变化规律的影响,提出3种焊缝建模方式:即完整焊缝模型,粗略焊缝模型与无焊缝模型。首先进行初始轴长比为1.8的椭球壳的液压胀形实验研究,得到轴长随内压力的变化规律。其次进行了3种建模方式的椭球壳胀形过程的数值模拟,对比数值模拟和实验过程轴长变化规律,分析建模方式对模拟精度的影响。结果表明:在变形初期,3种建模方式的模拟精度相近,尺寸偏差均小于4%;但是在变形中后期,无焊缝模型的模拟精度较差,最大尺寸偏差达15%;粗略焊缝模型和完整焊缝模型都能较好地预测轴长的变化规律,且尺寸偏差不超过5%。综上所述,粗略焊缝模型既能简化建模方式,又能较好地预测椭球壳胀形过程轴长的变化规律。
焊缝模型;椭球壳;液压胀形
椭球形容器具有重心低,容积大,受风面积小和外观优美等特点,适合于作为大型水塔、石油化工容器、容器封头等结构。由于椭球壳体的曲率半径从极点到赤道逐渐变化,采用模压成形工艺,一种直径的椭球壳需要多套模具,这是限制椭球壳体广泛应用的主要原因。为了解决传统模压成形工艺存在的问题,提出了采用无模液压成形方法制造薄壁椭球壳[1,2]。其基本过程:先由钢板裁出若干侧瓣和二块极板,侧瓣经过辊弯成为单曲率壳板,然后把这些单曲率壳板组装焊接成封闭多面壳体,向封闭多面壳体内充满水介质后,再通过一个加压系统向封闭多面壳体内施加内压,在内压作用下,壳体产生塑性变形而逐渐趋向于设计要求的椭球壳体。椭球无模液压成形技术主要优点:不需要模具和压力机,可降低成本;因为不需要模具,生产周期缩短,产品变更容易;经过超载胀形和整形,降低了焊接残余应力,提高了尺寸精度。

本文提出椭球壳胀形过程的3种建模方式,通过数值模拟结果与实验数据进行对比,分析了不同建模方式对数值模拟精度的影响,并给出了合理的焊缝区域有限元建模方式。
1 材料及有限元建模方式
1.1 椭球壳结构与材料
图1所示为理想受内压旋转椭球壳结构,其中a为椭球壳的长轴,b为椭球壳的短轴,轴长比λ=a/b。图2所示为胀形前椭球壳结构,壳体由12片侧瓣与2个极板通过TIG焊接工艺焊接为一个整体,其初始外接椭球壳的长轴尺寸为225mm,短轴尺寸为125mm,初始轴长比为1.8。两极板间初始距离为240mm,极板直径为126mm。图中A和B为测量点位置,其中A点为赤道面上焊缝点、B点为极点。
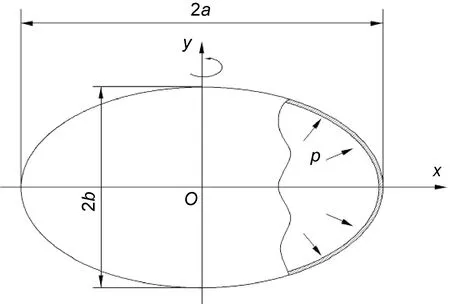
图1 理想受内压椭球壳结构Fig.1 Ideal ellipsoidal shell subjected to internal pressure
椭球壳的材料为不锈钢304,初始壁厚为0.9mm。从宏观力学差异看,TIG焊接工艺的不锈钢焊接接头可以分为3个区域:即焊缝熔化区,焊缝热影响区和母材。焊缝熔化区和热影响区的有效宽度根据垂直于焊缝方向的维氏硬度测试结果确定。其中熔化区和热影响区的宽度均约为3mm。参照国标GB/T228-2002标准制备熔化区,热影响区和母材的拉伸试样。拉伸后母材与焊接接头的真实应力-应变曲线如图3所示。
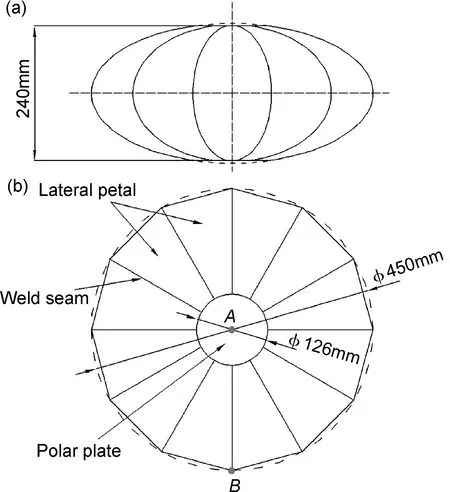
图2 胀形前椭球壳结构 (a)正视图;(b)俯视图Fig.2 Pre-form shell structure (a)front view;(b)up view
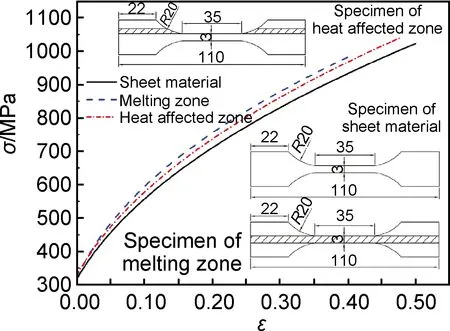
图3 母材与焊接接头真实应力-应变关系Fig.3 True stress-strain curves of sheet materials and weld seam
1.2 有限元模型
设计3种有限元建模方式:一是无焊缝模型,二是粗略焊缝模型,三是完整焊缝模型。图4(a)所示为完整焊缝模型,建模过程包含母材,热影响区和熔化区。图4(b)所示为粗略焊缝模型,建模过程只考虑了母材和熔化区,忽略了热影响区。图4(c)所示无焊缝模型,建模过程只考虑母材,忽略了热影响区和焊缝。
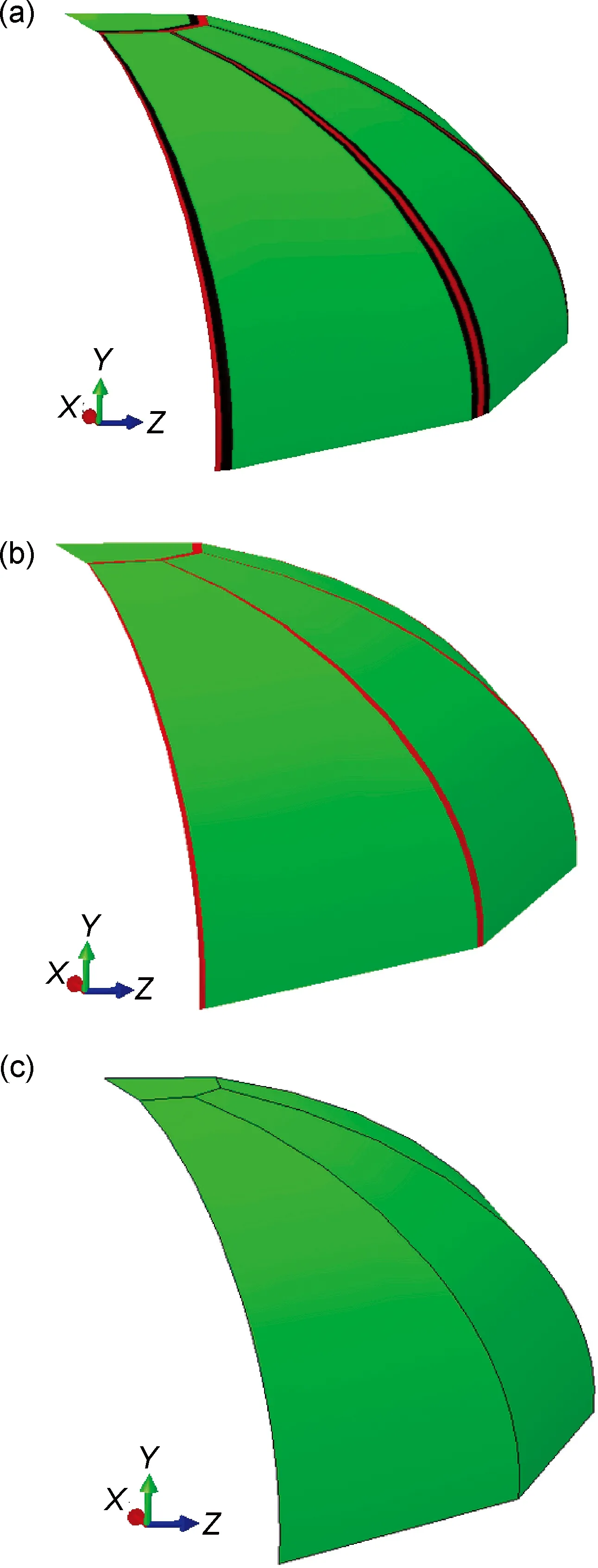
图4 有限元建模方式(a)完整焊缝模型;(b)粗略焊缝模型;(c)无焊缝模型Fig.4 Weld seam model (a)comprehensive model; (b)rough model;(c)no weld seam model
采用通用有限元分析软件ABAQUS对椭球壳变形过程进行分析,考虑到椭球壳的几何对称性,取八分之一椭球壳。有限元分析中不考虑侧瓣的装配焊接过程以及焊接后的残余应力和变形,只考虑室温下壳体、焊缝及热影响区的塑性变形。建模过程,根据单向拉伸实验结果,单独赋予壳体,焊缝和热影响区的材料属性和截面属性。材料属性均为符合Mises屈服准则的各向同性的材料的模型,网格类型均为四边形线性缩减积分壳单元S4R。内压力施加于壳体内表面,并随时间线性增加。
2 椭球壳无模液压成形实验研究
图5所示为轴长比为1.8的椭球壳胀形前多面体预制坯的制造过程,首先先由钢板裁出12个侧瓣和两块极板,侧瓣经过辊弯成为单曲率壳板,然后把这些单曲率壳板通过点焊的组成封闭多面壳体,最后通过TIG焊工艺完成整个封闭多面壳体结构的焊接。

图5 椭球壳胀形前结构制造过程 (a)下料;(b)辊弯;(c),(d)装配+点焊;(e)焊接Fig.5 Manufacture process of pre-form shell (a)blanking; (b)roll-bending;(c),(d)assembled by spot welding;(e)welding
实验过程以水为变形介质,并通过加压系统向封闭多面壳体内施加内压。实验过程严格记录不同压力下,长轴和短轴的变化规律。图6所示为实验过程不同成形压力时,椭球壳的形状。从图6可以看出,随着内压力的升高,椭球壳结构逐渐趋向球壳结构。

图6 不同压力下椭球壳形状(a)2.2MPa;(b)3.8MPa;(c)6.8MPaFig.6 Variation of shell shape with the increasing of internal pressure (a)2.2MPa;(b)3.8MPa;(c)6.8MPa
图7所示为实验过程截面形状的变化。当椭球壳内表面施加内压力时,变形首先发生在极板处,短轴开始伸长;当内压力达到1.0MPa时,赤道带焊缝处出现皱褶;当压力达到2.2MPa时,起皱最严重;当压力达到3.8MPa时,皱褶消失,赤道面形状恢复到与初始状态相似的正十二边形,长轴有一定的收缩。随着内压力的持续增加,短轴继续伸长,长轴继续收缩,组成椭球壳的12个侧瓣在压力作用下逐渐圆弧化。当压力达到5.5MPa时,长轴从持续收缩状态转为伸长状态,短轴仍旧持续伸长。最终压力为6.8MPa,得到轴长比为1.06的椭球壳,接近于球形。此时短轴为205.8mm,长轴为218.5mm,相应的轴长变化率分布为64.6%和-2.9%。
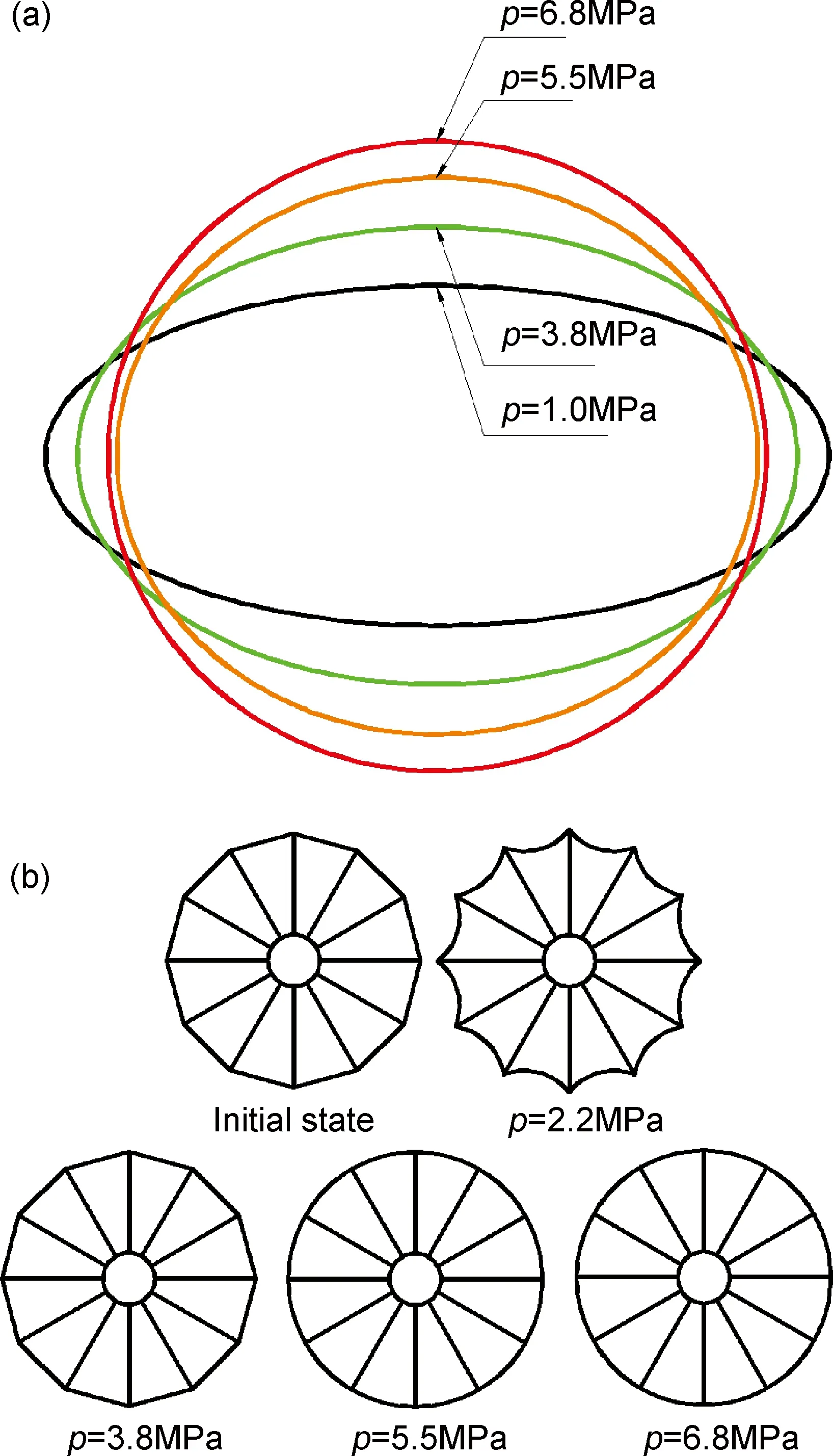
图7 不同压力下椭球壳截面变化(a)纵向截面;(b)赤道面Fig.7 Section variation of the ellipsoidal shell with the increasing of internal pressure (a)vertical section;(b)equatorial plane
3 数值模拟精度分析
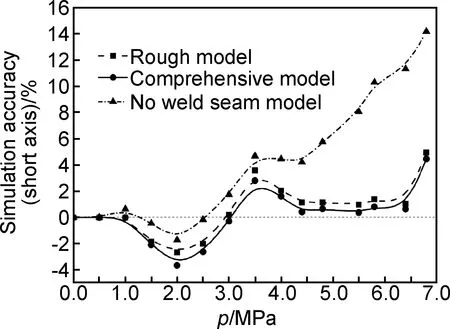
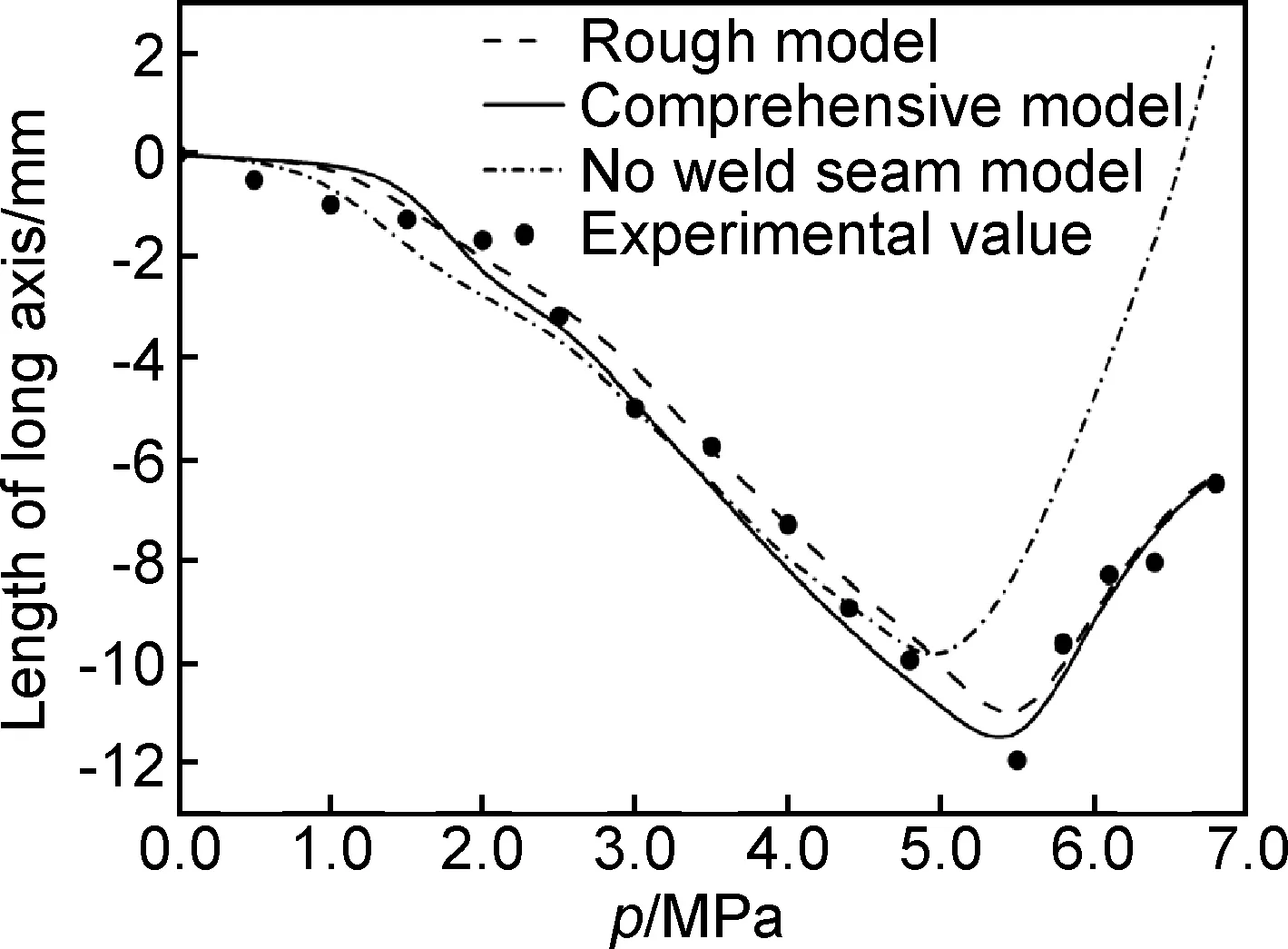
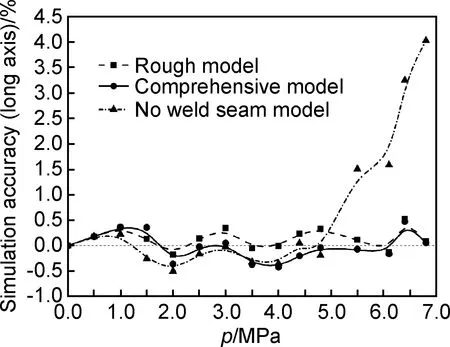
图8所示为不同建模方式对短轴变化的影响。从短轴的变化规律可以看出,在变形的前期(p≤2.5MPa),3种建模方式得到数值模拟结果与实验结果吻合较好。在变形中期(2.5MPa 图9所示为不同建模方式对短轴模拟精度的影响。尺寸偏差定义为:(Le-Ls)/Le,其中Le和Ls分别表示实验过程轴长和数值模拟过程轴长。在变形的前期,3种建模方式的数值模拟精度相近,其尺寸偏差在4%以内。在变形的中期和后期,完整焊缝模型和粗略焊缝模型仍旧保持较高的模拟精度,其尺寸偏差最大也不超过5%。但是无焊缝模型在变形中后期模拟精度较低,尺寸偏差较大。当模拟结束时,其尺寸偏差已经达到15%。显然在变形的中后期,无焊缝模型不能准确预测短轴变化规律。 图8 不同建模方式的短轴变化情况Fig.8 Variation of short axis for different weld seam models 图9 建模方式对短轴模拟精度的影响Fig.9 Effect of weld seam models on simulation accuracy of short axis 图10为不同建模方式对长轴变化的影响。从长轴的变化规律可以看出,在变形的前期和中期(p≤5.0MPa),3种建模方式得到数值模拟结果相差较小,且与实验结果吻合较好。在变形后期(5.0MPa 图10 不同建模方式时长轴变化情况Fig.10 Variation of long axis for different weld seam models 图11所示为不同建模方式对长轴模拟精度的影响。其中完整焊缝模型和粗略焊缝模型在整个过程均保持较高的模拟精度,其尺寸偏差最大也不超过1%。无焊缝模型在变形后期,模拟精度逐渐降低,尺寸偏差逐渐增大。当模拟结束时,其尺寸偏差已经达到4%。虽然在可接受范围内,但是无焊缝模型无法准确对长轴变化趋势以及拐点位置进行预测。 图11 建模方式对长轴模拟精度的影响Fig.11 Effect of weld seam models on simulation accuracy of long axis 由于焊缝和热影响区材料在性能上同母材有一定的差异,所以会导致变形有先后。同时,焊缝和热影响区作为一种更“硬”的材料,对母材的变形也是起到一定的约束作用。这也是在变形中后期,无焊缝模型精度预测较差的原因。但是从模拟精度上看,完整焊缝模型与粗略焊缝模型相差很小。所以为了简化建模方式,建立粗略焊缝模型即可满足需求。 (1)完整焊缝模型与粗略焊缝模型均可以很好地预测变形过程轴长的变化规律,最大尺寸偏差不超过5%。 (2)无焊缝模型在变形前期可以较好地预测椭轴长变化规律;但是在变形的中后期,对轴长的变化规律预测不准确,最大尺寸偏差达15%。 (3)粗略焊缝模型既能保证模拟精度,又可以简化建模方式。 [1] YUAN S J, ZENG Y S, WANG Z R. The integral hydro-bulging forming of ellipsoidal shells[C]∥Proceedings of the 5th International Conference on Technology of Plasticity. Columbus: American Society of Mechanical Engineers, 1996: 943-946. [2] ZHANG S H, ZENG Y S, WANG Z R. Theoretical analysis and experimental research into the integral hydro-bulge forming of oblate shells [J]. Journal of Materials Processing Technology, 1996, 62(1):199-205. [3] ZENG Y S, YUAN S J, WANG F Z, et al. Research on the integral hydro-bulge forming of ellipsoidal shells[J]. Journal of Materials Processing Technology, 1997, 72(1):28-31. [4] YUAN S J, ZHANG W W, TENG B G. Research on hydro-forming of combined ellipsoidal shells with double generating lines[J]. Journal of Materials Processing Technology, 2015, 219(5):124-132. [5] ZHANG W W, TENG B G, YUAN S J. Research on deformation and stress in hydro-forming process of an ellipsoidal shell without constraint[J]. International Journal of Advanced Manufacturing Technology, 2015, 76(9-12): 1555-1563. [6] ZENG Y S, WANG Z R, YUAN S J. The numerical simulation of the integral hydro-bulging of ellipsoidal shells[J]. Journal of Materials Processing Technology, 1997,72(3):358-362. [7] ZHANG S H,NIELSEN K B, DANCKERT J, et al. Integral hydro-bulge forming of pressure vessel heads [J]. Journal of Materials Processing Technology, 1999, 86: 184-189. [8] 王仲仁,曾元松. 内压椭球壳塑性变形的发生部位与扩展过程分析[J]. 固体力学学报,1998,19(1):85-88. WANG Z R,ZENG Y S. Occurring and expanding of the plastic deformation in ellipsoidal shell subjected to internal pressure[J]. Acta Mechanica Solida Sinica, 1998,19(1):85-88. [9] 王仲仁,曾元松,苑世剑,等. 椭球壳体液压成形的塑性变形规律的研究[J]. 固体力学学报,1998,19(3):259-264. WANG Z R,ZENG Y S, YUAN S J, et al. The research on plastic deformation of the hydro-bulge forming of ellipsoidal shells[J]. Acta Mechanica Solida Sinica, 1998,19(3):259-264. [10] YUAN S J, HU L, HE Z B, et al. Research on two-step hydro-bulging forming of ellipsoidal shell with larger axis length ratio[J]. Journal of Harbin Institute of Technology, 2013, 20(3): 93-98. [11] 胡蓝,滕步刚,何祝斌,等. 用中心管限位的椭球壳无模液压成形试验研究[J]. 压力容器,2011,28(4):1-6. HU L, TENG B G, HE Z B, et al. Research on die-less hydro-bulge forming of ellipsoidal shells with central tube constraint[J]. Pressure Vessel Technology,2011, 28(4):1-6. [12] WANG J C, MA N S, MURAKAWA H, et al. Prediction and measurement of welding distortion of a spherical structure assembled from multi thin plates[J]. Materials and Design, 2011,32: 4728-4737. [13] 崔俊华,柯黎明,刘文龙,等. 搅拌摩擦焊接全过程热力耦合有限元模型 [J]. 材料工程,2014, (12):11-17. CUI J H, KE L M, LIU W L, et al. Thermo-mechanical coupled finite element model for whole process of friction stir welding[J]. Journal of Materials Engineering, 2014, (12): 11-17. [14] 罗雅,雷玉成,龚辰诚,等. V对MGH956合金TIG原位合金化焊接接头组织与性能的影响[J]. 材料工程,2015,43(1):59-65. LUO Y, LEI Y C, GONG C C, et al. Effects of V on microstructure and properties of MGH956 alloy welding joints with TIGin-situalloying[J]. Journal of Materials Engineering,2015, 43(1):59-65. [15] 黄丽婷,陈明和,谢兰生,等. 超声冲击载荷对CP3钛合金焊接接头残余应力的影响[J]. 航空材料学报,2014, 34(1): 52-55. HUANG L T, CHEN M H, XIE L S, et al. Influence of ultrasonic impact load on residual stresses distribution of welded joints for CP3 titanium alloy[J]. Journal of Aeronautical Materials,2014, 34(1): 52-55. (本文责编:杨 雪) Research on Weld Seam Models for Hydro-forming of Ellipsoidal Shell ZHANG Wei-wei1,TENG Bu-gang1,2 (1 School of Materials Science and Technology,Harbin Institute of Technology,Harbin 150001,China;2 National Key Laboratory of Precision Hot Processing of Metals,Harbin Institute of Technology,Harbin 150001,China) In order to study the effect of weld seam models on hydro-forming of ellipsoidal shell, three kinds of models,i.e., comprehensive model rough model and no weld seam model were built and the influence was discussed on variation of axis length. An experiment for hydro-forming of ellipsoidal shell with initial axis length ratio 1.8 was first carried out, and the axis length varying with the increasing of internal pressure was obtained. Simulation on three kinds of finite element model was conducted, and the effect of weld seam models on the simulation accuracy was deeply discussed by a comparison of axis length variation between simulation and experiment. It is shown that little difference happens among the three kinds of weld seam models at the early stage of deformation, and the axis length deviation is less than 4%. However, there is worse simulation accuracy for the no weld seam model at the middle and late stage of deformation, and the axis length deviation is up to 15%. While both the comprehensive model and the rough model can successfully predict the axis length variation with the deviation no more than 5%. Finally, the rough model is selected on the basis of better simulation accuracy and simple weld seam model. weld seam model;ellipsoidal shell;hydro-forming 10.11868/j.issn.1001-4381.2015.000098 TG409 A 1001-4381(2017)03-0060-06 长江学者和创新团队发展计划资助(IRT1229) 2015-01-20; 2015-07-20 滕步刚(1969-),男,教授,博士生导师,主要从事塑性成形理论与塑性加工工艺研究, 联系地址:黑龙江省哈尔滨市西大直街92号哈尔滨工业大学材料楼420室(150090),E-mail:bgteng@hit.edu.cn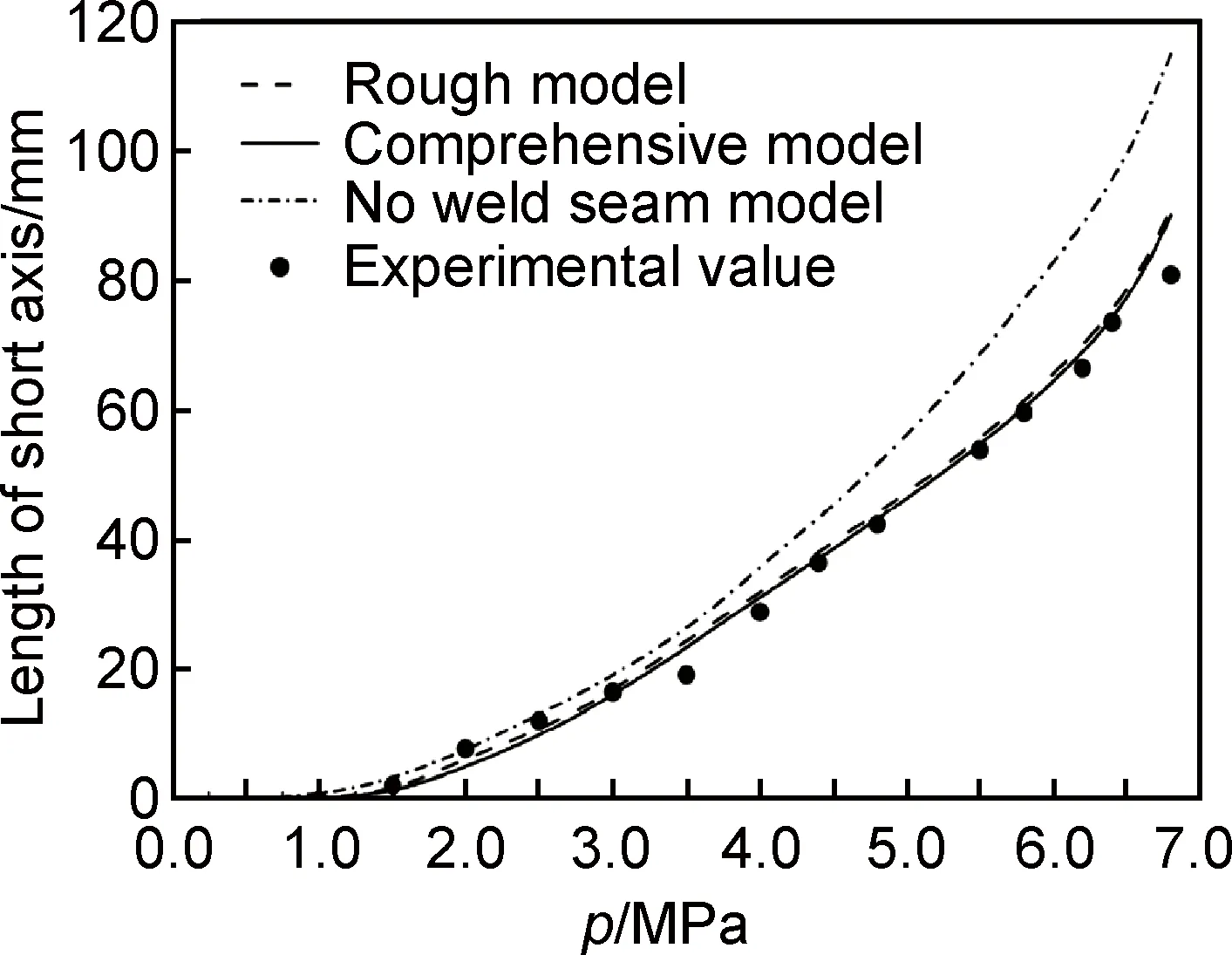
4 结论

