弱收敛在勒贝格积分中存在性证明及其具体应用
吴志勇
(遵义师范学院 继续教育学院, 贵州 遵义 563002)

弱收敛在勒贝格积分中存在性证明及其具体应用
吴志勇
(遵义师范学院 继续教育学院, 贵州 遵义 563002)
为了证明勒贝格积分是否具有弱收敛性,基于勒贝格相关理论,得到勒贝格积分存在弱收敛的充要条件为{fk}在Lp空间中有界;同时,得出需满足{fk}在测度E范围内的积分极限值等于其积分值的条件.最后,将勒贝格积分应用在概率统计方面,并采用Lebesgue-Stieltjes积分分别表示随机变量及数学期望. 关键词: 勒贝格积分; 弱收敛; 测度; 概率统计; 随机变量; Lebesgue-Stieltjes积分
勒贝格控制收敛定理的证明及其应用是经典实变函数论中的重要课题,得到了相当广泛深刻的研究.勒贝格Lp可积函数空间中的收敛性以勒贝格积分中的各种收敛性质为工具,深入到测度收敛、集中紧致、补偿紧致等[1].虽然勒贝格积分已经应用于少数领域之中[2],但目前有关空间勒贝格积分中的许多收敛性是分散在各文献中,大部分没有系统全面地总结[3].本文通过阐述黎曼积分及勒贝格积分理论,研究弱收敛在勒贝格积分中存在性证明及其具体应用.
1 黎曼积分定义
设f(x)是[a,b]上的有界函数,任意分点满足以下关系[4],即
(1)
如果将区间[a,b]分成n部分,对小区域[xi-1,xi]内的任意一点ξi(i=1,2,3,…)求和,有
(2)
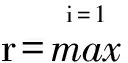
(3)
2 勒贝格积分定义
2.1 分划
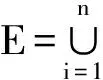
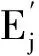
引理1 给定E任意两个分划D′,D,必存在比其细的第3分划,即
(4)
2.2 大和与小和
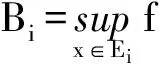

(5)
2) 设分划D′比D细,则s(D,f)≤s(D′,f),S(D,f)≤S(D′,f);
3) 对于任两个分划D′,D,有s(D,f)≤S(D′,f);
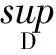
设f(x)是E⊂Rq(mE<∞)的有界函数,
(6)
分别称为f(x)在L上、下积分,当f(x)满足
(7)
则称f(x)在E上L可积,并称此共同值为f(x)在E上的L积分,记为∫Ef(x)dx.
以上是Rq中测度有限可测集上有界函数的L积分定义,形式上同R积分完全类似.除了积分区域更一般之外,主要不同之处在于采用的测度和分划的不同[4].
2.3 有界函数的勒贝格积分
设f(x)定义在E⊆Rq测度有限集E上的有界函数[7],
(8)
分别称为f(x)在E上的L上、下积分.
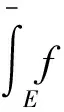
2.4 勒贝格积分的充要条件
设f(x)是定义在E⊂Rq测度有限集E上的有界函数[8],则f(x)在E上L可积的充要条件为:对任何ε<0,存在E的分划D,使
(9)
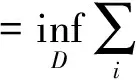
定理1 设f(x)是定义在E⊂Rq测度有限的集E上的有界函数,则f(x)在E上L可积的充要条件是f(x)在E上可测.
定理2 设f(x)在E上L可积,且f(x)=g(x),a.e.于E,则g(x)在E上L可积,且∫Ef(x)dx=∫Eg(x)dx.
根据上述阐述的黎曼积分与勒贝格积分定义可知,黎曼积分在实际应用过程中存在一定的局限性,而勒贝格积分的可积范围更加广泛,有效地克服黎曼积分的局限性.
3 勒贝格积分弱收敛存在的充要条件
3.1 强收敛与弱收敛定义
1) 设X是赋范线性空间,X为X′共扼空间,{xn}⊂X′,如果存在f∈X′,有

(10)
则称{xn}强收敛于x.
2) 设X是赋范线性空间,{xn}⊂X,如果存在f∈X,使得∀f∈X*,有
(11)
根据强收敛与弱收敛定义,强收敛必定弱收敛,但弱收敛不一定强收敛.
3.2 勒贝格积分弱收敛存在的充要条件
设Ω为Rn中可测集,测度mesΩ>0,{fk}在Lp(Ω)(1≤p≤∞) 弱收敛于f∈Lp(Ω).
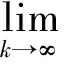
设‖fn‖≤M(n=1,2,…),f∈Lp(Ω),令φ∈Lp′(Ω)(1-p′<∞),根据函数集在Lp(Ω)上的稠密性,当m无限大时,则有任意的δ>0,满足
(12)
令k→∞,ε→0,δ→0,则有
(13)
因此,{fk}弱收敛于f的充要条件为
1) {fk}在Lp(Ω)中有界;
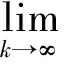
如果f∈Lp(Ω)1 (14) (15) 由此可知,当p=1时,式(13)关系不成立. 证明 充分性.由于f∈Lp(Ω),因此对于任一的ε>0,均存在无限大的m,满足 (16) (17) 由于积分具有绝对连续性,因此,任一e⊂Ω,mese<δ,满足 (18) 根据叶果洛夫定理,fk→f, x∈Ωm,对于以上的δ>0,存在F⊂Ωm,使mes(Ωm-F)<δ,fk→f在F内是一致收敛的,则有 (19) 根据上述充分证明,有 (20) 由于式(20)中的ε>0具有任意性,则存在ε,有 (21) 根据定理3,必要性显然是成立的. 4.1 Lebesgue-Stieltjes积分理论 4.2L-S积分表示的随机变量函数 设ξ=(ξ1,…,ξn)为(Ω,A,P)的n维随机变量,其中,分布函数为F(x1,…,xn),gkk=1,…,m是n维实空间的有限Borel函数.若ηk=gk(ξ1,…,ξn)(k=1,…,m),则有 (22) 根据L-S积分定义[10],有 (23) 4.3 L-S积分表示的数学期望 若ξ=(ξ1,…,ξn)为(Ω,A,P)的n维随机变量,其中,分布函数为F(x1,…,xn)是n维实空间的有限Borel函数,则η=g(ξ1,…,ξn)存在数学期望则需满足如下2个条件. 1) 分布函数F(x1,…,xn)存在积分; 2) Eη=Eg(ξ1,…,ξn)=∫…∫g(x1,…,xn)dF(x1,…,xn). 证明 根据积分变换定理,有 (24) 式(24)中:左、右两端分别等于 (25) 4.4 实例应用 设随机变量ξ的分布函数为F(x),随机变量的分布函数为η=aξ+b(a,b均为实数);η=cosξ. 证明 令Fη为η的分布函数,有 (26) 式(26)中:G={x,ax+b (27) 式(27)中:G={x,cosx 勒贝格积分的创立,是弥补了黎曼积分的不足.文中在介绍勒贝格积分概念的同时,证明了勒贝格积分弱收敛存在的充要条件;同时,将勒贝格积分应用在概率统计上,并采用Lebesgue-Stieltjes积分分别表示随机变量及数学期望. [1] 赵建英,李海英.函数空间类Vitali覆盖证明及其应用[J].华侨大学学报(自然科学版),2016,6(2):88-91. [2] 杨洁.关于可测函数数列各种收敛性的几点注记[J].工科数学,1998,14(2):120-123. [3] 程基嚷,张奠宇,魏国强,等.实变函数论与泛函分析基础[M].北京:高等教育出版社,2003:121-122. [4] 姚建武.极限与三种收敛之间的关系[J].陕西教育学院学报,2003,19(1):70-73. [5] 赵目,赵玉华.关于弱收敛的一些结果[J].安徽教育学院学报,2007,25(3):9-10. [6] 黄永峰.也谈黎曼积分与勒贝格积分的区别及联系[J].时代教育(教育教学),2011,31(9):212-214. [7] 刘皓春晓.勒贝格控制收敛定理及其应用[J].品牌:下半月,2015,13(3):67-68. [8] 柴平分.关于可测函数列积分的收敛性[J].青海师范大学学报(自然科学版),1996,21(2):33-35. [9] 侯英.勒贝格控制收敛定理的应用[J].中国新技术新产品,2010,22(23):12-15. [10] 何婷妹.浅析黎曼积分与勒贝格积分[J].科技经济导刊,2016,36(14):321-323. (责任编辑: 陈志贤 英文审校: 黄心中) Existence Proof of Weak Convergence in Lebesgue Integral and Its Application WU Zhiyong (College of Extended Education, Zunyi Normal College, Zunyi 563002, China) In order to prove the Lebesgue integral is of weak convergence, basing on Lebesgue theory, we prove the necessary and sufficient conditions for the existence of the weak convergence of Lebesgue integral sequence {fk} are that the sequence are bounded inLpspace; at the same time, it must satisfy that the integral limit value of {fk} in the measure range ofEis equal to the integral value. Finally, by the application of Lebesgue integral to probability statistics, we use Lebesgue-Stieltjes integral to represent the random variables and mathematical expectation respectively. Keywords: Lebesgue integral; weak convergence; measure; statistical probability; random variable; Lebesgue-Stieltjes integral 10.11830/ISSN.1000-5013.201702026 2017-02-14 吴志勇(1963-),男,副教授,主要从事函数论的研究.E-mail:zysfjks484@163.com. 贵州省高校人文社会科学资助项目(2015JD114) O 10 A 1000-5013(2017)02-0271-05
4 勒贝格积分在概率中的应用
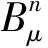
5 结束语

