采用MCMC方法的上海股市随机波动模型
赵慧琴, 刘金山
(1. 广东财经大学 华商学院, 广东 广州 511300;2. 华南农业大学 数学与信息学院, 广东 广州 510642)

采用MCMC方法的上海股市随机波动模型
赵慧琴1, 刘金山2
(1. 广东财经大学 华商学院, 广东 广州 511300;2. 华南农业大学 数学与信息学院, 广东 广州 510642)
采用贝叶斯统计中的马尔科夫链-蒙特卡罗(MCMC)方法对上海股市的随机波动性进行研究,基于Gibbs抽样的MCMC数值计算过程,对上海股市的随机波动率模型(SV)进行参数估计,并在WinBUGS软件中实现.根据信息判别准则(DIC),对比拟合的SV-N,SV-T,SV-MT模型参数,结果表明:SV-T模型最能反映上海股市波动具有尖峰厚尾的特性,可进一步用于预测样本外的波动率结果. 关键词: 随机波动率模型; 马尔科夫链-蒙特卡罗方法; 股市波动; 贝叶斯分析; 上海股市
经济或金融时间序列均存在着普遍的波动性现象,随机波动率模型(SV)可以模拟和预测波动状况.近年来,随机波动率模型在我国得到了不断的发展,研究者们提出一种最常用的扩展模型,即标准模型(SV-N模型)[1-3].SV族模型较难找到精确的似然函数,需要模拟建立完全的似然函数进行参数估计,如马尔科夫链-蒙特卡罗(MCMC)方法.国内已有一些相关研究,但较少将SV族的SV-MT,SV-T模型与SV-N模型进行比较分析[4-7].因此,本文基于贝叶斯统计中的MCMC方法,结合Gibbs抽样,对SV族的模型参数进行估计.
1 SV族模型的统计结构
1.1 SV-N模型
标准的SV模型形式[8]为
(1)
(2)
式(1),(2)中:yt为t时刻的标准化对数收益率;θt为对数波动,服从一个持续性参数为φ的高斯自回归AR(1)过程;误差项εt与ηt是不相关的,都服从均值0,方差σ2的正态分布;对于|φ|<1,SV模型的协方差是平稳的.
潜在波动θt的分布为
(3)
yt|θt的分布为
(4)
若令φ=2φ1-1,τ=σ2,且y1:n=(y1,y2,…,yn)′,θ1:n=(θ1,θ2,…,θn)′,根据Kim等[9]提出的方法,假定模型参数φ,τ,μ,θ1的先验分布为
μ,φ,τ,θ0的先验分布联合密度函数为
(5)
根据贝叶斯定理,后验分布的参数为
(6)
式(6)中:L(μ,φ,τ,θ0:n)为SV模型的似然函数.
1.2SV-T模型
SV-T模型表示一个混合的正态分布模型,其形式为
(7)
(8)
式(7),(8)中:εt服从自由度为w>2的t分布.
若假定λt服从倒伽马分布,是一个潜在的变量,则有
(9)
(10)
(11)
取参数ω的先验分布ω~χ2(8),其他参数的先验分布同SV-N模型[10].w和θt的后验条件分布为
(12)
1.3SV-MT模型
SV-MT模型形式为
(13)
(14)
式(13),(14)中:εt为服从自由度为w>2的t分布.
在模型中,d的先验分布近似服从正态分布,其他参数的先验分布与SV-T模型参数相同.μ,τ,φ的后验条件分布也与SV-T模型参数相同,即
(15)
1.4 模型的比较
基于贝叶斯方法,采用信息判别准则(DIC)[11-12]对SV模型进行比较,具体形式为
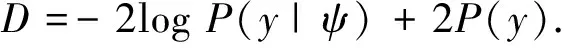
(16)
DIC准则可以很好地比较复杂的统计模型,即
(17)
2 上海股市SV族模型参数的贝叶斯估计
在SV族模型中,其参数用MCMC方法中的Gibbs抽样进行估计.数据源于新浪财经网2013年9月2日至2014年8月29日的上海股市的收盘价格,共242个数据.在进行模型参数的贝叶斯估计前,用WinBUGS软件对模型参数进行10 000次预迭代,再进行20 002次迭代,以保证参数的收敛性.3种模型参数的贝叶斯估计,如表1所示.由表1可知:波动水平参数μ在SV-N模型中的绝对值较大,说明在SV-N模型中上证综指的波动性体现得比较强烈;3个模型中的波动持续性参数φ的估计值相差不大,都在0.98以上,说明3个模型都能刻画上证综指收益率序列的波动持续性,也说明我国股市具有波动集聚性;在SV-T和SV-MT模型中加入自由度参数ω,其值分别为16.260,16.480,体现了上海股票尖峰厚尾的特性[13],而SV-N模型并未体现这一特性.SV-T模型参数的后验核密度估计,如图1所示.

表1 SV族模型参数的贝叶斯估计

(a) ω的核密度 (b) μ的核密度

(c) φ的核密度 (d) τ的核密度图1 SV-T模型参数的后验核密度估计图Fig.1 Posterior density function for SV-T model

表2 各模型的DIC值的比较
明3个模型中,模拟上海综指的数据最好是SV-T模型,最差是SV-N模型;对于PD值的模拟,SV-T模型最大,而SV-MT最小.说明对于上海综指的模拟,SV-MT模型相对于其他模型来说是最简单的模型,而SV-T模型是最复杂的;对于综合了模型的复杂度和拟合优劣的DIC值,SV-T模型的值最小,其值为389.676,而SV-N模型的值最大,其值为398.868,这说明在模拟上海股市波动特性时,SV-T模型要优于SV-N模型和SV-MT模型.
3 结束语
对SV-T,SV-N,SV-MT模型的参数估计、后验核密度估计和DIC值进行比较,可以得出在模拟我国上海股市的波动性中,SV-T模型比SV-N,SV-MT模型更优,更能反映上海股市的尖峰厚尾的特性,并且证明了上海股市具有很强的波动持续性.利用SV-T模型,可进一步用于预测样本外的波动率结果.对于国外已有的杠杆SV模型[14]、长记忆SV模型[15-16]研究,将是今后进一步研究的方向.
[1] NAKAJIMA J,OMORI Y.Leverage, heavy-tails and correlated jumps in stochastic volatility models[J].Computational Statistics and Data Analysis,2009,53(6):2535-2553.
[2] BROTO C,RUIZ E.Estimation methods for stochastic volatility models: A survey[J].Journal of Economic Surveys,2004,18(5):613-649.
[3] WANG J J J,CHAN J S K,BORIS C S T.Stochastic volatility models with leverage and heavy-tailed distributions: A Bayesian approach using scale mixtures[J].Computational Statistics and Data Analysis,2011,55(1):852-862.
[4] 王泽锋,史代敏.基于DIC准则的ASV模型和SV模型的实证比较[J].数量经济技术经济研究,2007,24(5):134-141.
[5] 顾锋娟,岑仲迪.基于GADCH类模型和SV类模型的泸深两市波动性研究[J]. 数学的实践与认识,2011,41(1):14-22.
[6] 朱慧明,李峰,杨锦明.基于MCMC 模拟的贝叶斯厚尾金融随机波动模型分析[J].运筹与管理,2007,16(4):111-115.
[7] 何永涛,王飞.随机波动模型贝叶斯估计效率研究[J].统计与信息论坛,2015,30(4):7-14.
[8] TAYLOR S J.Modeling stochastic volatility[J].Mathematical Finance,1994,4(2):183-204.
[9] KIM S,SHEPHARD N,CHIB S.Stochastic volatility: Likelihood inference andcomparison with ARCH models[J].Review of Economic Studies,1998,65(3):361-393.
[10] MEYER R,YU Jun.BUGS for a Bayesian analysis of stochastic volatility models[J].Econometrics Journal,2000,3(2):198-215.
[11] SPIEGELHALTER D J,BEST N,CARLIN P B.Bayesian measurements of model flexibility and fit (with discussion)[J].Journal of Royal Statistical Society,2002,64(4):583-639.
[12] 蔡晓薇.MCMC方法下最优Copula的估计及选取[J].统计与信息论坛,2011,26(10):33-38.
[13] 邱世斌,陈燕武.马尔可夫链在前沿资产组合中的应用[J].华侨大学学报(自然科学版),2009,30(2):221-224.
[14] LSHIHARA T,OMORI Y,ASAI M.Matrix exponential stochastic volatility with cross leverage[J].Comuputational Statistics and Data Analysis,2016,100(8):331-350.
[15] SO M K P,KWOK S W Y.A multivariate long memory stochastic volatility model[J].Physica A,2006,362(2):450-464.
[16] HO H C.Sameple quantile analysis for long-memory stochastic volatility models[J].Journal of Econometicle,2015,189(2):360-370.
(责任编辑: 钱筠 英文审校: 黄心中)
Stochastic Volatility Modeling of Shanghai Stock Exchange Using MCMC Method
ZHAO Huiqin1, LIU Jinshan2
(1. Huashang College, Guangdong University of Business Studies, Guangzhou 511300, China;2. College of Mathematics and Informatics, South China Agricultural University, Guangzhou 510642, China)
One method is by Markov chain Monte Carlo (MCMC) bias statistics method. In this paper, we study the stochastic volatility of Shanghai Stock market, and estimate the parameters of the stochastic volatility model (SV) of Shanghai Stock market based on the MCMC sampling, and implement the Gibbs software in the WinBUGS software. By comparingthe parameters of SV-N, SV-T, SV-MT model, and according to discriminative information criterion, we find the SV-T model is the best model in China reflecting the fluctuation of the stock market of Shanghai which has peak thick tail characteristics, this model can also be used to step out of sample forecasting volatility results. Keywords: stochastic volatility models; Markov chain Monte Carlo method; stochastic volatility; Bayesian analysis; Shanghai Stock
10.11830/ISSN.1000-5013.201702024
2017-02-14
赵慧琴(1982-),女,讲师,博士,主要从事经济统计和概率统计的研究.E-mail:zhq_6285144@163.com.
广东省青年创新人才类重点课程建设项目(2014WQNCX177); 广东省质量工程经管综合实验教学中心建设项目(2013年度); 广东省质量工程统计学专业实验教学示范中心建设项目(2014年度)
O 212
A
1000-5013(2017)02-0262-04

