双端面磨削砂轮直线修整中最佳修整参数的研究

周志雄 谢 沈 舒 阳 许世雄 彭关清 唐湘平

1.湖南大学机械与运载工程学院，长沙，4100822.宇环数控机床股份有限公司，长沙，410323

双端面磨削砂轮直线修整中最佳修整参数的研究

周志雄1谢 沈1舒 阳1许世雄2彭关清2唐湘平2

1.湖南大学机械与运载工程学院，长沙，4100822.宇环数控机床股份有限公司，长沙，410323

根据双端面磨削原理,分析并确定砂轮直线修整相关的设计参数。以磨削区域内上下砂轮端面形状为研究对象，建立磨削区域的几何方程并进行分析计算，得到上下砂轮端面高度在工件几何中心运动轨迹上的变化曲线。分别确定固定式修整及插补式修整的最佳修整参数，获得磨削区域中理想的砂轮端面几何形状，提高工件的加工精度和精度稳定性,降低工件表面粗糙度。

双端面磨削；磨削区域；修整参数；几何形状

0 引言

随着汽车行业、轴承行业和IT业的蓬勃发展，双端面磨床因其高效率、高精度及高自动化程度等特点得到了快速的发展。特别是近年来,随着智能手机行业的兴起，双端面磨床被应用于磨削手机玻璃片，拓展了双端面磨床的应用领域，同时也对机床的加工精度、效率、稳定性提出了更高的要求。市场需要能够一次完成粗磨、半精磨、精磨、光磨工序的高效、高精度双端面磨床，由此减少设备投入成本、加工时间、劳动力成本及设备维护费用。国内外许多学者为提高双端面磨床的加工精度及效率进行了深入分析研究。文献[1-3]对双端面磨床的总体设计进行了理论分析研究。文献[4]根据恒磨除率原理，提出了一种送料盘变速控制方法。文献[5]研究了工件自旋转磨削原理，获得了很好的工件表面磨削纹理。文献[6]对双端面磨削砂轮的端面形貌进行了数学建模分析。文献[7-9]对双端面磨削区域特性及材料去除率的变化进行了分析研究。文献[10]利用矩阵变换法计算双端面砂轮任意点的坐标。以上文献没有针对双端面砂轮修整进行系统的研究。为此，本文从双端面磨削原理出发，建立几何方程并进行计算分析，确定最佳修整参数，获得理想的砂轮磨削区域的几何形状，使工件在磨削过程中完成粗磨、半精磨、精磨、光磨工序。

1 双端面磨削及直线修整方式

双端面磨削方式如图1所示，即在上下砂轮间形成倾角，工件通过送料盘旋转带动，从两砂轮端面开口的高点处开始进料，从最低点出料，从而达到去除工件余量的目的。上下砂轮绕自身轴线旋转(两砂轮一般转速相同，转向相反)，送料盘4顺时针回转，工件5从上料位处上料并装夹到送料盘4的装载孔内，在送料盘4的带动下进入磨削区，到下料位处脱离送料盘下料，完成磨削加工。

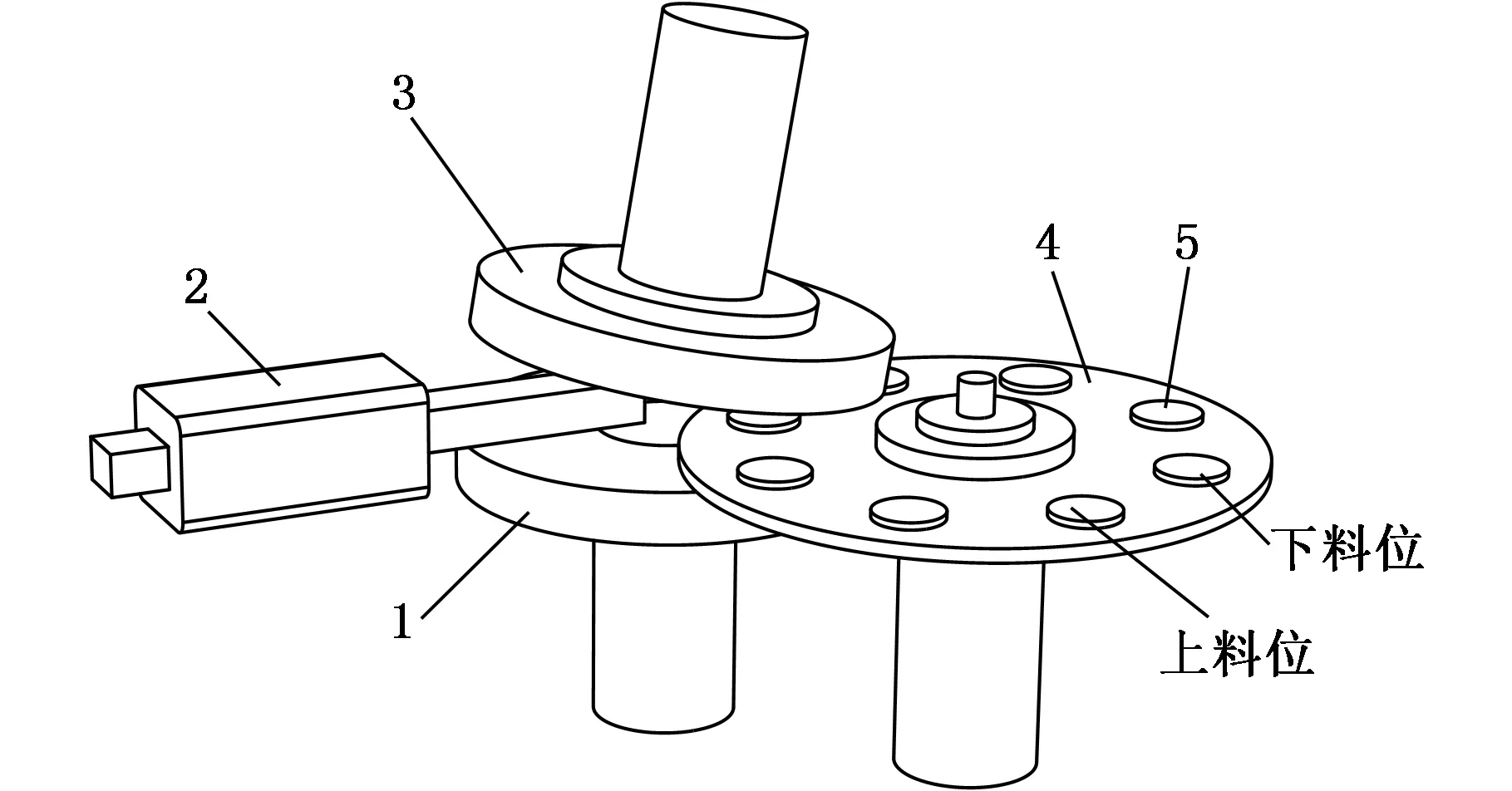
1.下砂轮 2.直线修整机构 3.上砂轮 4.送料盘 5.工件图1 双端面磨削运动原理图Fig.1 Diagram of double disc grinding

砂轮工作一段时间后，砂轮端面磨粒变钝，需要修整机构对砂轮进行修锐。通过直线修整机构上安装的两个金刚笔对上下砂轮端面同时进行修整[11]。直线修整机构在与下砂轮端面平行的平面上进行直线往复修整运动。由于金刚笔修整平面与下砂轮端面平行，修整完成后下砂轮端面仍为平面。而上砂轮倾斜一定角度，修整金刚笔在直线方向上修整的同时，上砂轮绕自身轴线进行回转运动。因此上砂轮端面为一绕自身轴线回转的曲面，同时回转轴在竖直方向上倾斜一定角度，故相对于下砂轮端面来说为一空间复杂曲面。砂轮修整后上下砂轮间形成了一个复杂的磨削区域，如图2所示。

图2 上下砂轮形成的磨削区域Fig.2 Grinding area formed by upper and lower grinding wheels

上砂轮修整后的端面形状将直接影响磨削区域中工件余量在磨削运动轨迹上的变化曲线，从而影响工件的加工精度。工件余量在磨削过程中的去除方式大致分为三类，如图3所示。

(a)磨削速率恒定 (b)磨削速率由慢至快 (c)磨削速率由快至慢图3 磨削过程中工件磨削余量的变化曲线Fig.3 Curve of grinding allowance

图3a中，工件余量在磨削过程中以近似恒定的速率被去除；图3b中，工件余量在磨削过程中的前半段比较平缓地被去除，后半段则被快速地去除；图3c中，工件进入磨削区域的初期被快速去除，实现粗磨，然后去除速率逐渐下降，最终在脱离磨削区域时工件的余量去除率接近零，从而达到光磨的目的，降低工件的表面粗糙度。此外，工件最终的尺寸公差、平行度、粗糙度都是由出口点处决定的。图3a和图3b中工件离开磨削区域时还在进行余量的去除，砂轮边缘处容易损耗，因此工件的加工精度低，精度稳定性差；图3c中工件离开磨削区域时基本不进行余量去除，处于光磨阶段，砂轮边缘处损耗小，不会对工件加工精度产生很大影响，有利于工件加工精度的稳定性。

综上所述，有必要对磨削区域修整后的形状进行分析研究，确定最佳修整参数，使磨削余量按照图3c所示的曲线变化。

2 砂轮直线修整的相关参数分析

图4中,O1为下砂轮回转中心、O0为送料盘回转中心，砂轮外径为D，孔径为D1，直线修整路径为过O1点、角度为ω的直线(ω以逆时针方向为正，顺时针方向为负)，上砂轮的倾斜平面在水平方向上的角度为β，O1O0的距离为L，工件几何中心绕O0点作圆弧运动的直径为d1，工件的外切圆直径为d2,内切圆直径为d0，送料盘的外径为d3，α0为工件几何中心出口点处与O0点连线相对于O1O0所成角度，α1为工件在任一磨削位置处工件中心与O0点连线相对于O1O0所成的角度。在图5中，E-E截面上砂轮的轴线在垂直方向上相对于下砂轮轴线的倾斜角度为θ，上砂轮围绕球心O摆动，实现对倾斜角度θ的调节，其中球心O与上砂轮金刚笔修整平面的垂直距离为H，上砂轮开口量为h(上砂轮端面最高点与最低点的差值)，上砂轮最低点距下砂轮修整端面的距离为A。

图4 砂轮直线修整几何参数关系Fig.4 Geometric parameters of wheel linear dressing

图5 上下砂轮位置关系Fig.5 The upper and lower grinding wheel

上砂轮倾斜角度θ的计算公式为

(1)

为使上下砂轮磨削端面全部被修锐，工件外切圆d2须超出砂轮内孔D1一定距离，一般取3 mm，即

(2)

以圆形工件为研究对象，工件直径为d，则

d1=d2-d=2L-D1-d+6(mm)

(3)

d0=d2-2d=2L-D1-2d+6(mm)

(4)

工件的理论平行度就是工件在出口点处上砂轮端面边缘(在竖直方向上为一抛物线)对工件磨削成形后产生的高度差ΔH,即

(5)

以YHDM580B双端面磨床为例，砂轮外径D=585 mm,精磨时砂轮开口量h=0.1 mm,工件的理论平行度随工件直径d变化曲线如图6所示。

图6 工件平行度变化曲线(理论)Fig.6 Curve of workpiece parallelism in theory

由式(5)看出工件的理论平行度与d2和h成正比，与D2成反比，与砂轮直线修整角度ω无关。实际中，工件平行度还受砂轮边缘损耗的影响。当修整角度ω取合适值，使工件磨削余量按照图3c所示的曲线变化，特别是工件在出口点处去除率为零时，砂轮边缘的损耗最小，工件平行度的一致性就好。

上砂轮的倾斜平面在水平方向上的角度β为

(6)

工件几何中心处的最大去除余量Δh为

Δh=h(2L+D+d1)(2L+d1-D)(2L+
D-d1)(D+d1-2L)/(16D2L2)

(7)

上砂轮最小修整量(即上砂轮端面完全被修锐时，上砂轮主轴进给量)ξ为

(8)

以YHDM580B为例，砂轮外径D=585 mm，孔径D1=195 mm，送料盘直径d3=760 mm，砂轮开口量h=0.1 mm，中心距L=449.5 mm，H=300 mm。取工件直径d=100 mm，可知d1=610 mm，α0=40.17°。上砂轮竖直方向上的倾斜角度θ=0.0098°，上砂轮倾斜平面在水平方向上的角度β=47.73°，工件几何中心位置最大去除量Δh=0.0452 mm。

3 固定式修整中最佳修整角度的确定

固定式修整就是，当修整金刚笔进入修整区域时上下砂轮只有回转运动而没有进给运动，砂轮竖直方向的坐标为固定值，修整一次完成后金刚石修整笔退出修整区域，上下砂轮才进给一次，通过多次进给实现对上下砂轮端面的修整。由于下砂轮端面修整后仍为平面，故只需研究磨削区域中上砂轮端面修整后的形状，取上砂轮金刚笔修整平面竖直坐标z=0。在金刚笔直线修整运动轨迹上任意一点P(Rcosω,Rsinω,0)绕上砂轮主轴回转得到点Q((d1/2)sinα1,(d1/2)cosα1-L,z)，点Q投影到z=0平面的投影点落在工件几何中心运动轨迹d1圆上，其中α1在[-α0,α0]区间内变化，如图7所示，图中ω为修整角度。

图7 砂轮修整三维关系图Fig.7 3D diagram of grinding wheel

3.1 上砂轮端面高度在工件中心运动轨迹的方程

上砂轮回转中心线的空间直线方程：

(9)

上砂轮回转中心线向量为

S=((d1/2)sinα0,(d1/2)cosα0-L,D2/(2h))

(10)

工件中心运动轨迹上球心点O(0,0,H)到任一点Q的向量为

OQ=((d1/2)sinα1,(d1/2)cosα1-L,z-H)

(11)

修整轨迹上点O(0,0,H)到任一点P的向量为

OP=(Rcosω,Rsinω, -H)

(12)

由几何关系，点Q与点P到回转中心线距离相等得

(13)

修整轨迹上一点与工件运动轨迹上一点的连线向量QP为

QP=((d1/2)sinα1-Rcosω,(d1/2)cosα1-
L-Rsinω,z)

(14)

由几何关系QP与回转中心线垂直得

QP·S=0

(15)

联立式(13)和式(15)，便可计算出z。式中d1、α0、L、D、H、h为已知量，z、α1、ω为未知量。当给ω赋值，便可得到自变量为α1、因变量为z的函数方程，如图8所示。

图8 上砂轮端面高度在不同修整角度ω下的变化曲线Fig.8 Curve of the upper grinding wheel height with different ω

(1)当ω=-β=-47.73°时，曲线在出口点处的斜率为-1.17×10-17，由于代入的数值存在有效位数，可以认为该点处的斜率为零，所得曲线为理想曲线。工件在进入砂轮磨削区域初期以近似恒定的去除率进行磨削，然后去除率逐渐减小，最后在出口点处去除率为零。从而使工件在磨削过程中完成粗磨—半精磨—精磨—光磨工序，同时又克服了砂轮边缘磨损对工件加工成形精度的影响。存在的不足是修整轨迹与送料盘干涉,修整装置没有安装位置。上砂轮最小修整量ξ=33.3 μm。

(2)当ω=-30°时，曲线在出口点处斜率为-2.5×10-3,从图中看出曲线在靠近出口处比较平坦，且修整轨迹避开了与送料盘干涉的位置，刚好为修整装置留有紧凑的安装空间，故为合理的修整角度。上砂轮最小修整量ξ=31.8 μm。

(3)当ω=-20°时，曲线在出口点处斜率为-5.9×10-3，从图8中看出曲线在靠近出口处斜率较大,工件在出口位置还在进行较大余量的去除，不能满足粗磨-半精磨-精磨-光磨要求。上砂轮最小修整量ξ=29.5 μm，修整量有所减小但变化不大。

综合上述分析并结合修整路径与送料盘干涉的临界修整角度为ω=-32.5°，故本文取ω=-30°为最佳修整角度，其位置关系如图9所示。

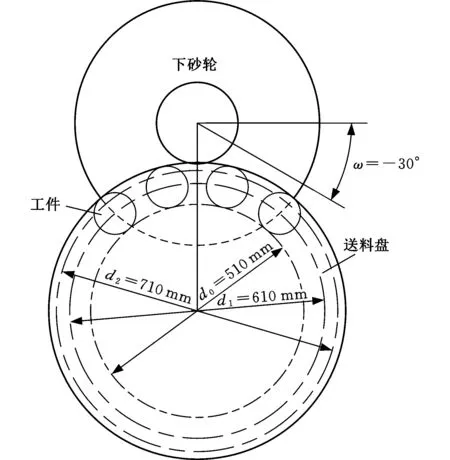
图9 修整角度ω=-30°位置关系图Fig.9 The position relationship with ω=-30°

修整角度ω=-30°时，在工件的三个重要参考点(两外侧点和中心点)的运动轨迹d0、d1、d2上，上砂轮高度相对工件转角α1的变化如图10所示。由图10可知，工件上各位置处在磨削后期相对长的范围内去除余量很小、且出口点处工件各位置的高度差接近于零，使工件能够获得较好的表面粗糙度、平行度，解决了砂轮边缘易损耗而影响加工精度的问题，保证了机床加工精度的一致性。

图10 上砂轮高度在不同磨削轨迹下的变化曲线(固定式)Fig.10 Curve of the upper grinding wheel height with different grinding path(fixed type)

4 插补式修整中最佳修整角度的确定

插补式修整就是，当修整金刚笔进入修整区域时上砂轮既有回转运动又有进给运动，上砂轮一边修整一边在竖直方向上插补进给。下砂轮则仍为固定式修整。插补式修整不存在固定式修整的修整位置受限制的问题，能够在任一位置上进行修整，获得与固定式修整中ω=-β=-47.73°时相同的理想砂轮形状。如图11所示，通过插补进给，上砂轮端面在插补修整路径O1K截面上任一点的坐标N为(ρcosω,ρsinω,z)，N点绕回转中心线旋转与直线O1F相交于M点，坐标为(rcos(-β),rsin(-β), 0)。

图11 插补式修整三维示意图Fig.11 3D diagram of interpolation dressing

由图11可知

ON=(ρcosω,ρsinω,z-H)

(16)

OM=(rcos(-β),rsin(-β),-H)

(17)

MN=ON-OM

(18)

则有：

(19)

MN·S=0

(20)

联立式(19)、式(20)得到ρ关于z的函数关系式。

上砂轮修整前端面高度z0为

z0=(D/2-ρcos(ω+β))/(Dh)

(21)

上砂轮主轴进给量为

δ=z-z0

(22)

上砂轮主轴进给量在不同修整角度ω下的变化曲线如图12所示。其中，不同修整角度ω对应的上砂轮主轴进给量随修整位置ρ变化曲线相重合，且近似于直线，控制系统编程易于实现：ρ=D/2时，进给量为0；ρ=D1/2时，上砂轮主轴向下进给33.3 μm。上砂轮端面插补修整后效果如图13所示。

图12 上砂轮主轴进给量在不同修整角度ω下的变化曲线Fig.12 Curve of upper grinding wheel feed with different ω

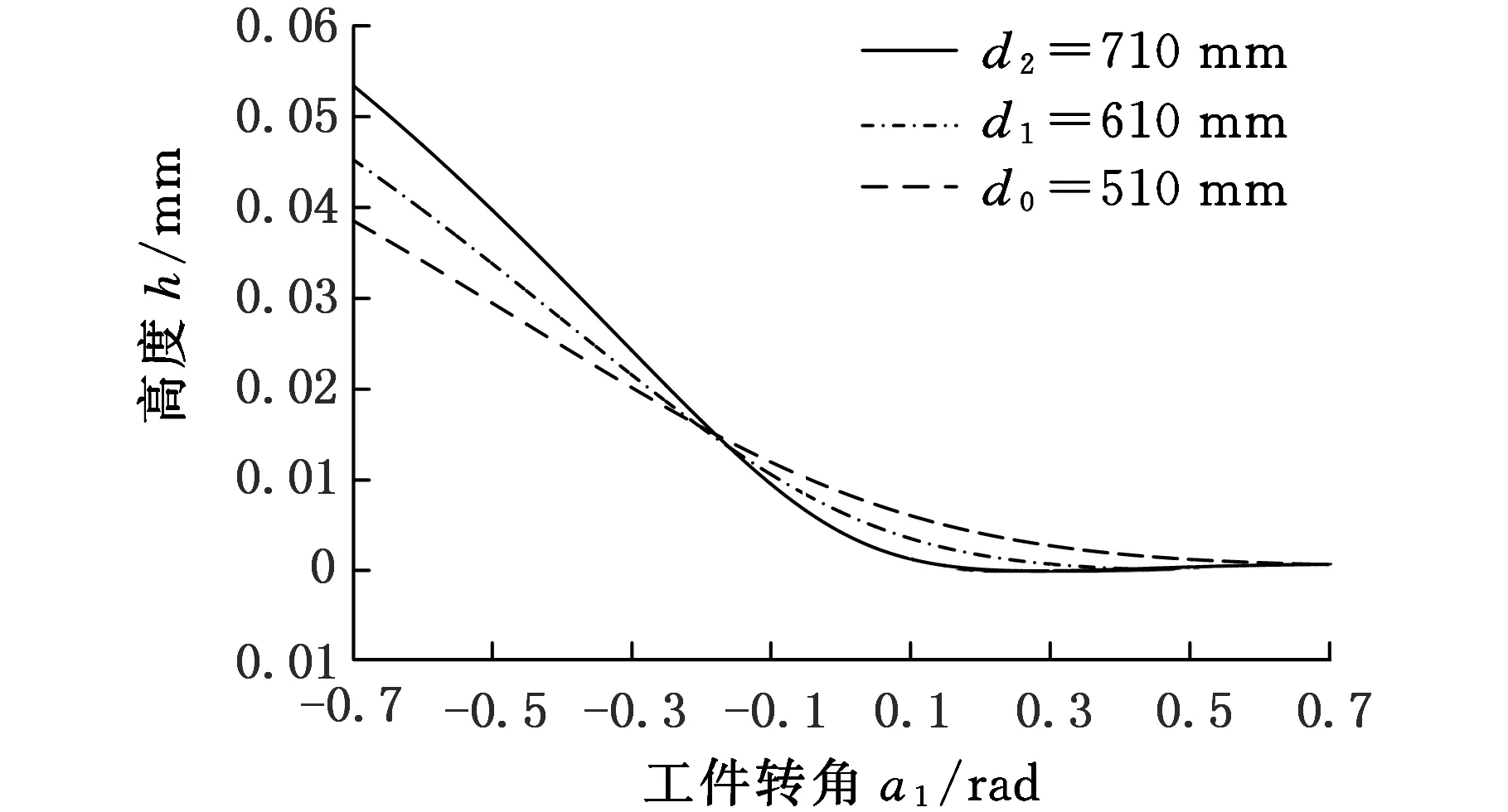
图13 上砂轮高度在不同磨削轨迹下的变化曲线(插补式)Fig.13 Curve of the upper grinding wheel height with different grinding path(interpolation type)

不同的修整角度ω通过插补式修整都能得到一致的理想上砂轮端面形状。考虑ω=90°时，修整机构便于安装拆卸，且有利于机床的整体布局及外观设计，故选用ω=90°为最佳修整角度。

5 实验验证

为验证上述分析的正确性，以插补式修整、修整角度ω=90°为实验对象，对砂轮实际修整后的端面形状与理论计算结果进行对比分析。同时检验机床加工精度及精度稳定性。实验条件如表1所示。砂轮修整与活塞环磨削实验参数见表2。

表1 活塞环磨削加工实验条件

表2 砂轮修整与活塞环磨削实验参数

由图14可知，砂轮实际修整后的端面形状与理论分析结果相近，验证了理论分析的正确性。分析误差产生的主要原因是砂轮端面修整后个别CBN磨粒的脱落及凸出。

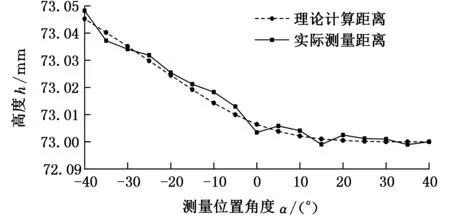
图14 上下砂轮端面距离在d1轨迹上的变化曲线Fig.14 Curve of distance between the upper and lower grinding wheel on d1 path

实验加工工件共200件，按照加工先后顺序对工件进行编号，逐一检测工件的厚度、平行度、表面粗糙度。对工件的厚度检测采用五点测量取平均值的方法，检验结果如图15所示。

图15 工件厚度变化曲线Fig.15 Curve of workpiece thickness

由图15可见，加工工件的厚度差在5 μm以内。加工初期，砂轮边缘损耗比较快，经过一段时间磨合后，工件厚度变化趋于稳定。

平行度采用德国Werth色彩聚焦探测器，沿定义的扫描轨迹对工件上下端面进行测量，并计算出工件的平行度几何公差，如图16所示，测量精度为0.1 μm。

由图16可见，工件的平行度在2 μm以下，达到很高的精度要求。加工后期的工件平行度小于加工前期，且随着加工的进行,工件平行度趋于平稳。说明砂轮经过磨合后机床加工精度的稳定性较好。

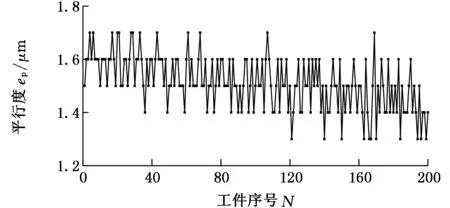
图16 工件平行度变化曲线(实验)Fig.16 Curve of workpiece parallelism in experiment

采用JB- 4C粗糙度仪测量工件表面粗糙度，测量精度为0.01 μm，测量结果如图17所示。由图17可见，随着加工的进行，工件表面粗糙度慢慢降低，最后保持在相对稳定范围内。

图17 工件表面粗糙度变化曲线Fig.17 Curve of workpiece surface roughness

以上实验结果与理论分析基本相符，验证了理论分析结果的正确性。

6 结论

(1)根据双端面的磨削原理,确定砂轮直线修整相关参数，保证了磨削区域几何方程的正确性。同时引入工件理论平行度及工件几何中心最大去除余量公式，可以分别确定砂轮开口量及砂轮主轴单次进给量的大小，为机床磨削加工工艺提供理论指导。

(2)固定式修整中修整装置有安装位置的限制，插补式修整则对主轴进给精度及控制系统要求较高。可根据实际需要选取不同的修整方式，从而确定最佳修整角度，获得理想的砂轮端面形状。

[1] 王洪，许世雄，申彬彬，等．双端面磨床的研究[J]．内燃机与配件，2011(3)：19-23．WANGHong,XUShixiong,SHENBinbin,etal.StudyonDoubleFaceGrinder[J].InternalCombustionEngineandAccessories, 2011 (3):19-23.

[2]HUHuiqing.GrindingofDoubleDiscGrindingMachine[J].ChineseJournalofMechanicalEngineering, 2005,18(1):1-4.

[3] 张曙伟．双端面磨床提高加工精度的分析与研究[J]．精密制造与自动化，2002(4)：9-11．ZHANGShuwei.AnalysisandResearchontheImprovementofMachiningAccuracyofDoubleFaceGrinder[J].PrecisionManufacturingandAutomation, 2002 (4):9-11.

[4] 王洪，戴瑜兴，许君，等．数控双端面磨床送料圆盘转速预测算法的研究[J]．中国机械工程，2013,24(10)：1315-1319．WANGHong,DAIYuxing,XUJun,etal.StudyonthePredictionAlgorithmofFeedDiscSpeedofNCDoubleFaceGrinder[J].ChinaMechanicalEngineering, 2013,24(10):1315-1319.

[5] 田业冰，金洙吉，康仁科，等．硅片自旋转磨削的运动几何学分析[J].中国机械工程，2005，16(20)：1798-1801.TIANYebing,JINZhuji,KANGRenke,etal.AnalysisofMotionGeometryofSiliconWaferSelfRotatingGrinding[J].ChinaMechanicalEngineering, 2005, 16(20):1798-1801.

[6] 彭金波，周志雄，许世雄，等．双端面磨削砂轮作业面形貌模型研究[J]．现代制造工程，2016(2)：78-83．PENGJinbo,ZHOUZhixiong,XUShixiong,etal.StudyontheSurfaceTopographyModelofDoubleEndGrindingWheel[J].ModernManufacturingEngineering, 2016 (2):78-83.

[7]PIETSCHGJ,KERSTANM.UnderstandingSimultaneousDouble-diskGrinding:OperationPrincipleandMaterialRemovalKinematicsinSiliconWaferPlanarization[J].PrecisionEngineering, 2005, 29(2): 189-196.

[8]ZARUDII,HANBS.DeformationandMaterialRemovalRateinPolishingSiliconWafers[J].JournalofMaterialsProcessingTechnology, 2003, 140(1): 641-645.

[9] 季萍，张岩，殷滨杰．双端面磨床加工滚子端面的磨削区特性分析[J]．哈尔滨轴承，2007，28(3)：10-12．JIPing,ZHANGYan,YINBinjie.TheGrindingCharacteristicsofDoubleRollerGrinderEndFaceProcessingAnalysis[J].HarbinBearing, 2007, 28 (3):10-12.

[10]HIRAOKAN,TAKAHASHIT.GrindingDisc-to-discDistanceDistributionCalculationinaDouble-discGrinder[J].JSAT, 2014, 58: 463-467.

[11] 张飞跃．双端面磨床无间隙直线修整器优越性及其应用[J]．精密制造与自动化，2002(4)：20-21．ZHANGFeiyue.TheSuperiorityandApplicationofDoubleEndFaceGrinderStraightLineTrimmer[J].PrecisionManufacturingandAutomation, 2002 (4):20-21.

(编辑 王旻玥)

Research on Optimal Dressing Parameters for Wheel Linear Dressing of Double Disc Grinding

ZHOU Zhixiong1XIE Shen1SHU Yang1XU Shixiong2PENG Guanqing2TANG Xiangping2

1.College of Mechanical and Vehicle Engineering,Hunan University,Changsha,410082 2.Yuhuan CNC Machine Tool Co.,Ltd.,Changsha,410323

The relevant design parameters of the wheel linear trim was analyzed and determined according to the principles of double disc grinding. Regarding the grinding wheel end surface topography as the research projects, some grinding zone geometry equations were established, calculated and analyzed to get the height curve of upper and lower wheel end surface on the workpiece geometric center trajectory. And then in order to obtain the ideal grinding wheel end surface geometric shape in the grinding zone, optimal dressing parameters of fixed trim and interpolation trim were determined respectively. These may improve the workpiece machining accuracy, accuracy consistency and reduce surface roughness.

double disc grinding; grinding zone; dressing parameter; geometric shape

2016-03-17

湖南省战略性新兴产业科技攻关项目(2014GK1021)

TG580.64

10.3969/j.issn.1004-132X.2017.06.002

周志雄，男，1953年生。湖南大学机械与运载工程学院教授、博士研究生导师。主要研究方向为复杂刀具的设计与制造、数控机床设备、切削磨削理论及其设备等。发表论文130余篇。E-mail:zhouzx8@sina.com。谢 沈，男，1990年生。湖南大学机械与运载工程学院硕士研究生。舒 阳，男，1990年生。湖南大学机械与运载工程学院博士研究生。许世雄，男，1954年生。宇环数控机床股份有限公司董事长。彭关清，男，1963年生。宇环数控机床股份有限公司总工程师。唐湘平，男，1982年生。宇环数控机床股份有限公司高级工程师。