时差无源定位系统多机编队动态布站优化*
曲长文 王昌海 冯 奇 周 强
(1.海军航空工程学院 烟台 264001)(2.92543部队 长治 046000)
时差无源定位系统多机编队动态布站优化*
曲长文1王昌海2冯 奇1周 强1
(1.海军航空工程学院 烟台 264001)(2.92543部队 长治 046000)
布站形式能够直接影响多站无源定位效果,合理的运动轨迹对于定位跟踪效果也有很大的改善。多机编队的动态布站问题可以归结为布站形式和飞行轨迹的优化问题,该文以Fisher信息阵的行列式为指标,将其转化为非线性规划问题,并采用分散搜索法获得全局最优解。此外,对于编队的最优航迹选择和重新布站的时间间隔进行了探讨,得到一些有价值的结论。仿真结果表明,针对多机编队提出的动态布站优化算法对于提高编队的定位精度有着明显的效果,具有很好的工程实用价值。
无源定位; 动态布站; 非线性规划; 多机编队; 全局最优解
1 引言
现代高科技局部战争的经验表明,制空权和信息快速获取能力已成为决定战争胜负最为关键的两个因素,两者密不可分。在这种背景下,多机无源定位跟踪系统因为具有信息融合能力、隐蔽性好、机动性强、探测距离远等优点,已成为获取战场信息的重要手段[1]。
无源定位跟踪系统的最优布站方式或航迹规划是国内外学者的研究热点之一。多站布站优化问题主要集中于只测角定位[1~6]和时差定位[7~11]体制下的布站优化,而且研究对象多是针对固定观测站。文献[1~3]研究了双站测向交叉定位系统中的最优交会角问题,推导了最小圆概率误差或最小模糊区面积准则下的必要条件,具有一定的工程指导意义;文献[4~6]在多站只测角定位体制下以最大化Fisher信息阵(Fisher Information Matrix, FIM)的行列式为准则,给出了FIM行列式的几种等价形式以及最优布站的一般性条件。对于时差定位系统,在测量误差等其他条件保持不变的情况下,布站形式直接决定了多站时差定位的精度。文献[7~9]以几何精度因子(Geometric Dilution of Precision, GDOP)作为定位精度指标,通过仿真的方法研究了几种布站形式对定位精度的影响,并定性给出了最优布站原则;文献[6, 11]推导了多站到达时间(Time of Arrival, TOA)定位的FIM及其行列式,文献[10]推导了多站时差定位的FIM及其行列式,它们均以FIM行列式最大为准则,采用解析法得出了相同的最优布站条件。
尽管文献[1~3,6,10,11]给出了最优布站的解析解,但却不能直接应用于多机编队无源定位系统的动态布站中,这主要是因为载机平台之间的通信距离通常远小于目标与飞行编队的距离,从而很难满足上述文献中给出的最优布站条件。文献[12]提出一种只测角无源定位跟踪系统最优机动方法,并以方位角变化率最大为准则从理论上给出并证明了最优轨迹方程;文献[13]根据最大化FIM行列式准则,以解析法给出了只测角无源定位跟踪系统的机动控制策略和最优轨线方程,并说明了最大方位角变化率准则和最大FIM行列式准则的工程运用。文献[14]总结了现有的航迹规划的方法,以FIM行列式最大为准则,通过引入机动约束和威胁约束条件,将多架无人机(Unmanned Aerial Vehicle, UAV)航迹规划问题转化为非线性约束规划问题,但文献给出的各观测平台最优轨迹各异与实际中的多机编队飞行情况不符。
本文研究场景为多机编队飞行对远距离固定目标进行时差定位,不仅给出在一段时间内飞行编队的最优布站形式,还要给出编队的最佳机动策略。为简化问题,本文暂不考虑机动限制和存在威胁源的情况。
2 动态布站算法
2.1 FIM行列式最大化指标
最优布站和航迹规划中常用的指标主要有表征定位精度的几何精度因子(GDOP)[7~9]、克拉美劳下限(Cramer-Rao Low Bound,CRLB)的迹[15]以及与定位模糊区体积成反比的FIM行列式[4~6,10,11,13,14]。GDOP通常根据一个时刻的观测信息进行计算,可以用作静态布站的指标,对于运动中的飞行编队并不适合。CRLB是无偏估计的理论下限并与采用的估计算法无关,以其作为指标具有更小的位置误差,并且可以采用位置误差和速度误差的加权值作为指标[15]。由于CRLB为FIM的逆阵,与计算CRLB的迹相比,FIM行列式的计算和分析更加简单方便[5,14],并且将FIM行列式最大作为指标与CRLB的迹最小基本等价。因此本文采用FIM行列式最大作为动态布站的性能指标。
设1架长机与M-1架僚机编队飞行,在二维平面内考察时差定位(定义不再赘述,见文献[6])的FIM行列式指标。为简化问题,假设各载机的到达时间测量误差为独立的具有相同方差的零均值高斯白噪声,对应的时差(或距离差)测量误差协方差如式(1)所示[6,10,11]:
(1)
式中,σr=cσt,c为电磁波传播速度,设为3×105km/s,σt为到达时间测量误差。
FIM可由式(2)给出[4~6]:
(2)
式中,F为2×2的FIM,Φ为非线性测量方程,X=[x,y]T为目标位置,RΦ为测量误差协方差阵。
可以根据式(2)推导出多机时差定位系统在k时刻的FIM,如式(3)~式(6)所示:
(3)
式中,
(4)
(5)
(6)
注意到式(3)是只进行一次测量的FIM,在白噪声的假设下,N次测量的FIM可以写作式(7)求和的形式:
(7)
多机时差定位系统的动态布站性能指标如式(8)所示:
(8)
式中取自然对数是因为FIM行列式数量级较大,表示比较多有不便,而且行列式取对数并不影响其特点,文献[14]也称之为D-优化准则。
2.2 动态布站的非线性规划
如前所述,文献[1~3,6,10,11]给出了FIM即其行列式在一次测量时的具体表达式,并通过解析的方法求出了FIM行列式最大时满足的必要条件,而根据本文的研究背景,飞行编队经过一段时间多次测量的FIM行列式难以以解析的形式表达,而且需要优化的参数不再关注于观测站相对于目标的位置参数,而是各僚机相对于长机的布站参数以及编队的飞行方向,因此文献方法不再适用。文献[14]将多架UAV的航迹规划问题转化为决定UAV当前时刻机动方向的非线性约束规划问题,这为解决飞行编队的动态布站问题提供了解决思路,因此解决多机编队动态布站问题的关键便是如何将其转化为非线性规划问题。
以初始时刻长机位置为坐标原点O,以长机指向目标为x轴,目标建立如图1所示的二维直角坐标系。为简化问题,本文假设飞行编队在一段时间内以速度v0匀速直线飞行,且各僚机与长机的相对位置关系在此期间内保持不变。因此在二维平面内,对于M架飞机组成的飞行编队的动态布站问题便可以转化为对一个飞行方向φ、M-1个僚机相对于长机的布站分布角θi以及M-1个僚机相对于长机的距离di的优化问题,各参数的几何意义由图1给出。

图1 飞行编队与目标的几何关系图
不考虑载机运动噪声和载机位置误差的影响,若给定长机的初始位置和编队动态布站的各个参数,则任意时刻各载机的位置均可以确定,如式(9)和式(10)所示:
(9)
(10)
(11)
(12)
(13)
根据图1所示,编队飞行方向角φ的取值范围为-π≤φ<π;僚机相对于长机的布站分布角θ取值范围为0≤θi≤θj<2π,其中i 综合以上,飞行编队动态布站的非线性规划问题为 (14) 若设定di=dmax,式(14)中仅考虑φ和θ的界定,从而式(14)可以进一步简化为 在二维空间内对目标进行时差定位至少需要三架飞机。图2为不同飞行方向条件下FIM行列式仿真图,图3为不同僚机布站角度情况下FIM行列式仿真图。由图可以看到FIM行列式对参数比较敏感,当某个参数变化时,FIM行列式改变比较大;FIM行列式存在多个极大值点,且在极大值附近比较平坦平滑,因此实际动态布站时若布站误差控制得较小,布站误差对于布站效果的影响也比较小。 图2 不同飞行方向条件下FIM行列式仿真图 FIM行列式多极值的特点意味着一般非线性规划方法(如罚函数法、梯度法等)的结果受初始值的影响比较大,因此必须寻找能够找到全局最优解得优化算法。文献[16]采用基于多起始框架(Multistart Framwork)下的分散搜索(Scatter Search)方法来寻找非凸非线性规划问题的全局最优解,这为解决动态布站问题提供了必备数学工具。 本文采用分散搜索法对式(15)进行求解,可以获得多个FIM行列式的极大值及对应的局部最优解,经观察发现所求得的FIM行列式的值基本可以分为两类,一类非常接近全局最大值,另一类则与最大值有较大差距。因此可以首先通过设置门限或聚类的方法对求得的诸多FIM行列式极大值选出较大的一类,然后在这类结果中合并相同的结果便可以得到动态布站问题的最优解和满意的次优解。本文之所以还要给出次优解的原因在于,次优解的行列式指标与最优解相比非常相近,但动态布站的各项参数却有着较大的差别,因此完全可以作为一种备选方案以利于飞行编队的实际应用。表1给出二维平面内三机动态布站的最优解及次优解。 图3 不同僚机布站角度情况下FIM行列式仿真图 仔细观察表1中计算结果可以看到,在前文所述的仿真背景下,采用编队最佳飞行方向在±78°,各僚机大致分布于长机飞行方向的前后两侧,这与陆基时差定位系统的常用的星形布站、倒三角形布站、菱形布站等[7~8]完全不同,体现了适于飞行编队布站的新特点;此外,编队的最优飞行轨迹有两条,且关于长机飞行方向即x轴对称。 表1 三机动态布站解 根据式(15)可以得到一段时间内飞行编队的最佳飞行方向和布站形式,但依然存在两个问题需要进一步探讨。首先,如表1结论,编队的最佳飞行方向受初始值的影响必然有两条,并且关于x轴对称,相应的布站几何关系也必然关于x轴对称。编队飞行一段时间之后,按照式(8)FIM行列式最大化指标重新优化飞行方向和布站形式时也必将有两条路径可以选择,如图4所示,则应该选择轨迹O1→O2→O31还是O1→O2→O32? 图4 编队飞行轨迹示意图 其次,在已有的航迹规划中,通常是根据当前时刻的观测站与目标的距离、速度等信息来决定下一时刻观测站的最佳机动方案[12~14]。在本文背景下,问题被简化为一段时间内飞行编队保持匀速直线飞行,那么应该多长时间进行一次飞行方向和队形的重新调整,以利于提高目标定位跟踪效果? 针对第一个问题,文献[13]在单站最优机动轨迹优化中也出现两条最优轨迹的选择问题,并通过解析论证的方式给出了相邻两个采样时刻如何选择最优轨迹,即始终保持观测平台的舷角不变[13]。然而本文难以给出多次测量的FIM行列式的解析式并进行分析论证,只能通过仿真的方法来验证类似的结论,即轨迹O1→O2→O31应优于O1→O2→O32。以二维空间中三机编队为例,其他仿真条件同第2节,以O3处的FIM行列式为指标,仿真结果如表2所示。通过表2中的数据即可以验证,始终保持目标在编队飞行方向的一侧有利于提高定位的精度,同时这也利于编队的飞行控制,降低飞机的机动性要求。 表2 最优飞行轨迹对比 第二个问题是关于如何选取编队重新布站的时间间隔。重新布站的时间间隔太短,则失去编队飞行的意义;间隔太长,减少了飞行编队的机动次数,但可能对定位精度的提高有所影响。下面以仿真的方法对重新布站的时间间隔进行研究,以二维空间中三机编队为例,仿真条件同第2节,采取不同的重新布站时间间隔时各飞机航迹如图5所示。 图5分别给出了重新布站时间间隔为30s、60s、240s和600s时的编队飞行航迹,并给出了若干时间点编队的具体布站形式。由图中可以看到,飞行航迹基本以螺旋形逼近目标,但采用不同的重新布站时间间隔时的飞行航迹也有着较大的差异。表3给出了测量总时间一定,采取不同重新布站时间间隔时FIM行列式、定位误差下限和主站与目标的相对距离的对比。 通过表3中的数据比对可以看到,在总的测量时间一定时,采用不同的布站时间间隔对于定位精度的影响比较小,距离定位精度差别在米级,主要差别在于编队与目标的相对距离。当间隔30s或600s重新布站时,飞行编队能够较快地接近目标,目标的定位精度也比较高,可以为有源雷达提供引导;当间隔120s~180s重新布站时,飞行编队能够较为缓慢地接近目标,目标的相对定位精度比较高,有利于保持无源侦察优势。因此实际飞行时具体采用多长时间进行重新布站,可以根据战术目的进行合理选择。 表3 不同布站时间间隔指标对比 图5 不同重新布站时间间隔的编队航迹 可以注意到,之前所有的讨论均基于假设目标位置确切已知,从理论上研究最优航迹和布站形式。当目标位置未知或只获得其估计值,可以将估计值代入式(7)、式(8)中来计算行列式指标,并求解最优布站形式和飞行方向,然后测量进一步提高目标定位精度并用于下一次编队的布站队形和飞行方向调整。这种思想简单实用,下面通过仿真来验证这种边规划边定位的算法有效性。以二维空间中三机编队为例,重新布站的时间间隔120s,其他条件同第2节;始终保持匀速直线飞行的三架飞机作为对比,飞行方向偏离目标45°;采用UKF算法对目标进行定位,给定目标初始位置估计值为(280km,20km),仿真结果如图6所示。 图6 边规划边定位效果仿真 由图6可以看到,边规划边定位算法的定位精度非常接近理想航迹规划的CRLB,并且与不经规划的定位精度相比具有明显的提高。这说明飞行编队进行动态布站能够更好地发挥编队优势提高定位精度,而且采用边规划边定位的方式对于定位精度的影响非常小,因此具有很好的工程实用价值。 本文研究了多机编队飞行的动态布站优化问题,以FIM行列式最大值为指标,通过非线性规划的方法对一段时间内编队应采取的最优布站形式和飞行方向进行优化,得到了一些有价值的结论,并给出了一种实用的边规划边定位的算法。此外,本文还对飞行编队动态布站的相关问题进行了探讨,并给出了编队的最优航迹。通过仿真表明,本文所提的动态布站算法以及边规划边定位算法是有效的,具有较高的工程实用价值。 [1] 修建娟,何友,王国宏,等.测向交叉定位系统中的交会角研究[J].宇航学报,2005,26(3):282-286. [2] 修建娟,王国宏,何友,等.纯方位系统中的定位模糊区分析[J].系统工程与电子技术,2005,27(8):1391-1393. [3] 白晶,王国宏,王娜,等.测向交叉定位系统中的最优交会角研究[J].航空学报,2009,31(2):298-304. [4] Adrian N. Bishop, Baris Fidan, Brian D. O. Anderson, et al. Optimality analysis of sensor-target geometries in passive localization Part 1-Bearing-only localization[C]//IEEE Intelligent Sensors, Sensor Networks and Information Processing Conference, Melbourne,2007:7-12. [5] Dogancay, K. and H. Hmam. Optimal angular sensor separation for AOA localization[J]. Signal Processing, 2008(88):1248-1260. [6] Adrian N. Bishop, BarB. Fidan, Brian D. O. Anderson, et al. Optimality analysis of sensor-target localization geometries[J]. Automatica,2010(46):476-492. [7] 俞志强,王宏远,武文.四站时差定位布站研究[J].电子学报,2005,33(12A):2308-2311. [8] 孙宝国,苗强,宋继林,等.布站形式对TDOA无源区域定位系统定位精度的影响[J].火力与指挥控制,2011,36(9):129-132. [9] 王成,李少洪,黄槐.测时差定位系统定位精度分析与最优布站[J].火控雷达技术,2003.32(1):1-6. [10] Dogancay, K. and H. Hmam. On optimal sensor placement for time difference of arrival localization utilizing uncertainty minimization[C]//in 17th European Signal Processing Conference. 2009:1136-1140.. [11] Adrian N. Bishop, Bar?? Fidan, Brian D. O. Anderson, et al. Optimality analysis of sensor-target geometries in passive localization Part 2-TOA localization[C]//IEEE Intelligent Sensors, Sensor Networks and Information Processing Conference, Melbourne, 2007:13-18. [12] 董志荣.纯方位系统定位与跟踪的本载体最优轨线方程及其最优轨线[J].指挥控制与仿真,2007,29(1):7-15. [13] 许志刚,盛安冬,陈黎,等.被动目标定位系统观测平台的最优机动轨迹[J].控制理论与应用,2009,26(12):1337-1344. [14] Dogancay, K. UAV path planning for passive emitter localization[J]. IEEE Transactions on Aerospace and Electronic Systems,2012,48(2):1150-1166. [15] Helferty, J.P. and D.R. Mudgett. Optimal observer trajectories for bearings-only tracking by minimizing the trace of the Cramer-Rao lower bound[C]//The 32nd IEEE Conference on Decision and Control, San Antonio,1993:936-939. [16] Ugray, Z. et al. Scatter Search and Local NLP Solvers A Multistart Framework for Global Optimization[J]. INFORMS Journal on Computing,2007,19(3):328-340. Dynamic Deployment Optimization of Multi-flight Formation Based on TDOA QU Changwen1WANG Changhai2FENG Qi1ZHOU Qiang1 (1. Naval Aeronautical and Astronautical University, Yantai 264001)(2. No. 92543 Troops of PLA, Changzhi 046000) The deployment of multiple sensors has a direct effect on the multi-sensor passive location, and a proper trajectory of a moving observer can evidently improve its passive location accuracy. Dynamic deployment of multi-flight formation can boil down to deployment of multiple sensors and optimization of flight heading. It can be translated into nonlinear programming by the determinant of Fisher information matrix criterion, with scatter search method applied to find the global optimal solution. What’s more, how to choose the optimal trajectory of the formation and how long to re-deploy the formation are discussed and some valuable conclusions are drew. Simulation results show that the optimization algorithm of dynamic deployment proposed in this paper visibly improves the accuracy of multi-flight formation passive location, making it meaningful in the engineering. passive radar, dynamic deployment, nonlinear programming, multi-flight formation, global optimal solution TN958.97 2016年9月11日, 2016年10月21日 曲长文,男,教授,博士生导师,研究方向:无源定位与跟踪技术、合成孔径雷达成像、目标检测与识别。王昌海,男,硕士,研究方向:无源定位与跟踪技术。冯奇,男,博士研究生,研究方向:无源定位与跟踪技术。周强,男,博士,研究方向:合成孔径雷达成像、目标检测与识别。 TN958.97 10.3969/j.issn.1672-9730.2017.03.0103 动态布站的仿真研究
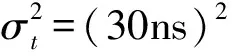





4 动态布站问题的进一步探讨与仿真





5 结语

